基于分层式控制的混合动力汽车生态驾驶研究 *

李亚鹏，唐小林，胡晓松

（重庆大学机械与运载工程学院，重庆 400044）

前言

汽车的生态驾驶旨在通过融合多源信息，耦合车辆系统与周围环境，从汽车驾驶工况优化到动力系统控制，实现车辆的驾驶性能提升。具有多动力源或执行机构的车辆，如混合动力汽车，多电机驱动纯电动汽车等，传统的动力系统工作效率提升方式等主要通过能量管理策略对功率/转矩进行分配或优化而实现［1］。由于这种方式并未参与到车辆行驶速度的规划，因此对提升车辆驾驶性能是有限的。现有车辆生态驾驶根据是否融合交通信号灯信息可分为两类。

对于没有融合交通信号灯状态信息的策略，如自适应巡航控制（adaptive cruise control，ACC），其利用由雷达或摄像头等元部件组成的感知系统，获取邻车的位置和行驶速度，进而调整本车速度与跟车距离，实现驾驶性能的提升［2-4］。一般ACC 控制的安全性通过控制跟车距离来实现，而其他性能，如驾驶舒适性与燃油经济性等，可以在给定安全范围内对速度进行优化［5-6］。在实际控制中，驾驶员需求与自动跟车控制会有一定差距，为此，Rahman等［7］提出了一种随机校正方法评估跟车模型中的参数分布，降低了真实需求与预测轨迹之间的差距。Li 等［8］设计了一种融合算法框架，在跟车过程中同时优化了车辆的驾驶舒适性与燃油经济性。Dib 等［9］基于反演法，将速度规划和能量管理问题建模为两个代数方程，实现了车辆驾驶性能的提升。Wang 等［10］将道路坡度作为优化变量，并用Markov chain 预测未来道路坡度变化，采用自适应动态规划的方法提升了车辆的燃油经济性。在实际中，交通信号灯状态对车辆行驶的影响不可忽视。为减少车辆因停车等待红灯的怠速油耗损失，Asadi 等［11］利用预测未来交通信号灯信息，并采用自适应巡航控制对车辆排的行驶速度进行了优化。Kamal 等［12］结合了广义最小残差法与模型预测控制（model predictive control，MPC），建立了动态交通道路模型，通过预测前车未来状态，提升了跟车的驾驶性能。Shao 等［13-15］建立了道路交叉口交通与车流模型，利用无迹卡尔曼滤波设计了一种交通状态预测方法，讨论了网联及非网联车辆混合车队的生态驾驶问题。

对于具有多变量多系统耦合的控制问题，在设计控制策略时需要考虑计算效率的问题。近年来，由于快速全局最优求解的特点，凸优化在电气化车辆的控制中得到了广泛关注［16］。为实现实时控制需求，将凸优化与模型预测控制算法相结合成为新的研究热点［17］。Johannessen等［18］针对混合动力汽车设计了一种分层式控制策略，不同控制层使用了不同拟合程度的车辆模型，其中上层在一定空间域内利用凸二次规划优化了车辆的速度轨迹，下层利用2阶锥规划（second-order cone programming，SOCP）解决动力系统能量管理问题。基于该研究思路，Murgovski 等［19］提出了一种协同自适应车辆排的经济性驾驶策略。Ghandriz 等［20］对比研究了序列线性规划与序列凸二次规划在实现混合动力汽车生态驾驶的不同。

上述研究大多集中在传统混合动力汽车的生态驾驶研究中，较少考虑插电式混合动力汽车。原因之一为插电式混合动力汽车需要对电量使用进行规划。在实时控制中，由于SOC 规划是一个非线性多变量控制问题，若采用最优控制算法解决该问题，则通常计算效率无法得到保障，因此现有研究大多集中在基于车辆行驶距离与行驶时间线性规划。为此，为兼顾算法的计算效率与计算精度，本文中设计了一种结合拟合近似的动力系统模型与高保真原始非线性模型的分层式控制策略，并在不同控制层采用了不同的优化算法，以提高车辆在智能交通环境中的驾驶性能。

1 道路交通与车辆动力系统建模

1.1 道路交通建模

在本研究中，假设车辆行驶道路长度为15 km，且道路上红绿灯有4 种类型，按照等间距循环布置的方式分布在道路上，每两个信号灯的间距假设为1 km，其中行驶起点距离第1 信号距离为0.5 km。4 种交通信号灯的信号相位与周期参数（signal phase and time，SPaT）见表1。为简单起见，假设车辆在黄色信号灯期间可以通行，因此将其统计在绿灯时间内。图1为所建立的道路交通模型。

图1 道路交通模型

表1 交通信号灯参数

1.2 车辆动力系统建模

本文所用动力系统模型为并联混合动力结构，如图2 所示。发动机与动力电池为两个单独的动力源，电池容量为11.39 kW·h，由1 500 个单体组成。发动机通过离合器与电机实现轴连接，动力电池通过逆变器与电机实现电力连接。电机输出轴端与一个变速器机械连接。各部件参数见表2。

图2 并联混合动力系统结构

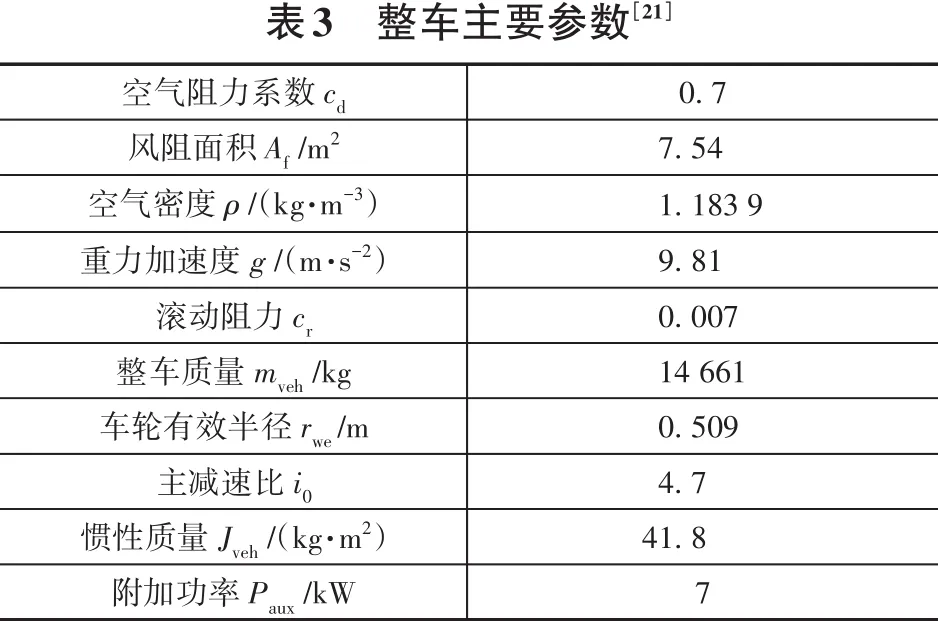
表2 动力系统部件参数［21］

根据车辆纵向动力学原理，在k时刻的需求力可根据下式计算：

式中：cd和ρ分别为空气阻力系数与空气密度；cr和β为轮胎滚动阻力系数和道路坡度；g为重力加速度；v（k）和a（k）分别为车辆在k时刻的速度与加速度；Af与mveh分别为有效风阻面积和整车质量。具体参数值见表3。

?

因此在变速器输入轴端的需求转矩与功率可计算为

式中：Tdem（k）、Pdem（k）分别为变速器输入轴端的需求转矩和功率；rw为车轮有效半径；i0为主减速比；ig（k）和ηg(k)分别为变速器在k时刻的传动比和传动效率；Jveh为车辆转动惯性质量；wdem为电机在k时刻的转速，rad/s。

故动力系统的转矩与功率平衡式为

式中：TICE（k）、TEM（k）和Tbrk（k）分别为发动机、电机和机械制动转矩；eon（k）为二元变量，eon（k）=1 表示离合器接合，发动机介入工作，eon（k）=0表示离合器断开，本文假设当需求转矩为正时eon（k）=1；PICE，output（k）、PEM，output（k）、Pbat，output（k）分别为发动机、电机和动力电池的输出功率；Paux为附加功率。

本文所用发动机模型的额定功率为90 kW，其万有特性如图3所示。发动机的功率平衡为

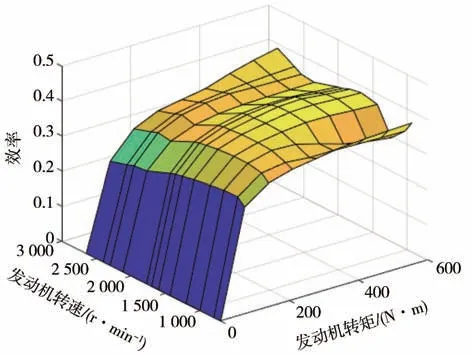
图3 发动机三维万有特性图

式中：TICE和wICE为发动机转矩和转速；ηICE为发动机工作效率；PICE，out为发动机输出功率；eon为离合器工作状态，eon=1 时表示离合器接合，发动机介入工作，eon=0时表示离合器断开。本文假设当需求功率为正时离合器接合。

本文所用电机模型为额定功率为110 kW 的永磁同步电机，如图4 所示。与发动机类似，其工作效率与转速、转矩有关。电机的功率平衡表达式为

图4 电机三维万有特性图

其中：TEM和wEM分别为电机转矩和转速；ηEM为电机工作效率；PEM，out为电机输出功率。

由于本文主要讨论车辆的能量管理问题，因此假设电池包的均衡控制是理想化的，故电池单体状态为电池包的状态：

式中：Ubat为电池单体开路电压；Rbat为电池单体内阻；Pbat，tot为电池单体总功率；Qbat为电池单体容量。

2 问题分析

2.1 速度规划问题

速度规划控制的目的是保证车辆在所有交通信号灯绿灯信号期间通过道路交叉口。得益于V2X技术及云计算技术，本文假设车辆在行驶过程中可以获得交通信号灯的状态，如图5所示。

图5 智能交通及V2X技术示意图

当车辆行驶接近交通信号灯时，信号灯状态有红灯和绿灯两种状态，如图6 所示。为确保车辆可以通过交叉口，需要计算出车辆的最大通过速度和最小通过速度。如最大通行速度应在红灯刚结束，绿灯刚开始时的速度，而最小通行速度为绿灯刚结束，红灯刚开始时的速度。因此，根据车辆状态与信号灯状态，车辆通过交叉口的速度计算式为

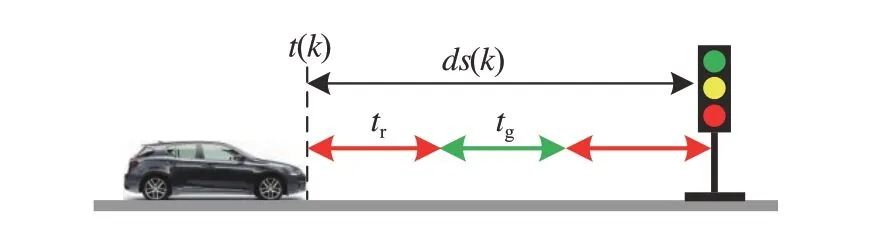
图6 车辆行驶状态

式中：vtarget_max（k）和vtarget_min（k）为车辆顺利通过交叉口的最大和最小速度；ds（k）为k时刻车辆当前位置距离前方最近交通信号灯位置的间距；tri、tgi和tci分别为红灯、绿灯和信号灯信i的号周期时间，且tci=tri+tgi；vroad_max为道路允许最大行驶速度，本文设置为15 m/s；Nkci为整数值，表示k时刻第i个信号灯的信号周期循环次数，当k=Nkcitci时，Nkci的值增加1。

利用上述速度边界求解公式，为提高车辆的驾驶性能，本文将速度规划问题转化为最优控制问题：

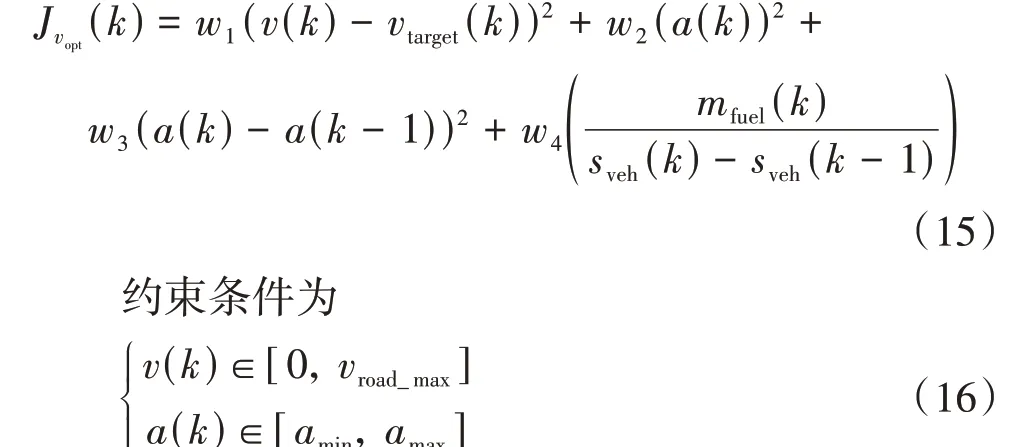
式中：wi（i=1，2，3，4）为权重系数；v（k）为需要优化的车辆速度；vtarget（k）为最优参考速度；a（k）为需要优化的加速度；mfuel（k）为等效燃油消耗；sveh为车辆在k时刻的位置。式（15）中的第1 项为确保车辆顺利通过路口，第2 项和第3 项为驾驶舒适性惩罚项，第4 项为最小单位距离等效燃油消耗。其中，vtarget（k）和mfuel的计算方式为

式中状态变量x和ẋ分别为车辆的位置和速度，控制变量u为加速度。

2.2 能量管理问题

混合动力汽车的能量管理旨在通过对发动机与电池的输出功率合理分配，实现车辆燃油经济性的提升。本文采用基于庞特里亚金最小值原理的等效燃油消耗最小值策略，其代价函数为

因此，基于ECMS的能量管理问题可表达如下：

minH(SOC，TICE，λ)状态变量：SOC控制变量：TICE约束条件：Tdem(k) = TICE(k)eon(k) + TEM(k) + Tbrk(k)Pbat，tot(k) = Pbat，out(k) + Paux Tbrk(k) ∈[- ∝，0]TICE(k) ∈[0，TICE，max(k)]TEM(k) ∈[TEM，min(k)，TEM，max(k)]Ibat(k) ∈[Ibat，min，Ibat，max]SOC(k) ∈[SOCmin，SOCmax]

由上式可知，协态变量对燃油经济性有重要影响，然而在实际行驶中，由于工况的随机变化特性，通常难以对协态变量进行精准求解，因此无法满足在行驶结束时最大限度使用电量的约束。为提高算法的自适应能力，有学者设计出基于行驶距离或行驶时间的线性SOC规划方法，其原理为在每一时刻根据实时SOC与线性规划出的参考SOCtrf差值，利用反馈控制对协态变量进行实时调整，通过这种自适应算法提高燃油经济性。然而该方法由于SOC规划的过程没有牵涉到优化，因此其对燃油的节省是有限的。另外一种方法是通过优化算法对SOC进行提前规划，然后利用反馈校正的方法对哈密顿函数中协态变量进行实时校正，实现对全局最优参考SOCref的跟踪。然而由于动力系统模型的非线性及多变量的特点，这种方式的计算效率无法得以保证。为此，本文提出了一种基于凸优化的参考SOCref快速规划方法，即通过对原始非线性模型进行拟合，将其转化为近似的凸模型，并利用凸优化算法快速计算出参考SOCref轨迹，然后在实时控制中根据误差对协态变量进行校正。具体凸优化的建模及算法框架可参考笔者以往的研究成果［21］，在此不在详细阐述。

3 算法框架

本文所提算法的控制框架如图7所示，包含3个控制层。在上层控制中，利用二次规划方法对问题式（15）进行求解，计算出全局最优参考速度，并将其输出给中间控制层。在中间控制层中，则利用凸优化算法求出全局参考SOCref，并传递给下层控制。具体算法步骤如下：

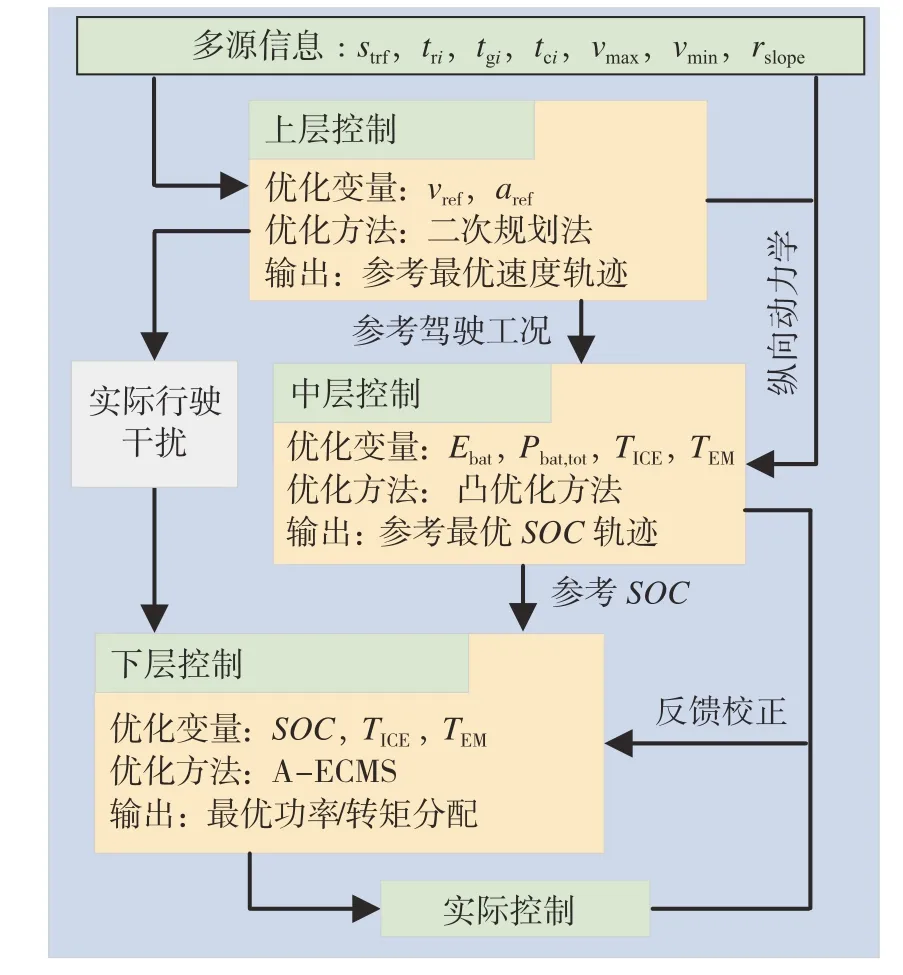
图7 控制原理简图

步骤1.基于QP计算参考速度，并将其储存到车辆计算机系统中；

步骤2.利用拟合的动力系统凸模型，基于2 阶锥规划计算参考SOCref，并储存到计算机系统中；

步骤3.设置增益系数Kp与ECMS的协态变量初始值，计算最优发动机和电机在k时刻的最优转矩分配；

步骤4.在k+1 时刻根据以下公式校正协态变量值：

步骤5.更新当前SOC状态；

步骤6.重复步骤3～5直到行驶结束。

图7 中，strf为红绿灯灯位置，vmax和vmin为道路允许最大与最小行驶速度，rslop为道路坡度。

4 仿真结果分析

本小节首先分析了所提策略的仿真结果，然后将优化后的车辆驾驶性能与没有对速度优化的策略进行了对比，并将燃油经济性与基于时间与路程线性SOC规划的两种策略进行了对比。

4.1 速度规划结果分析

为验证所提策略在驾驶性能提升上的有效性，在上层控制中，将结果与另外一种没有对速度优化的策略进行对比，该策略的速度计算方法为

图8 为两种速度规划策略下的车辆位置轨迹变化特性。由图可知，在前3 个道路交叉口，两种策略下的车辆轨迹几乎相同，但在第4 个交叉口与第14个交叉口出现了差别。当车辆在接近第4 个路口时，没有对速度优化的策略选择在当前绿灯窗口内通过，而所提策略则决定在下一个绿灯窗口内通过，在第14 个路口的情况与此类似。此外，两种策略均可以使得车辆在所有交叉口绿灯期间通过，避免了停车等待造成的怠速燃油损失。

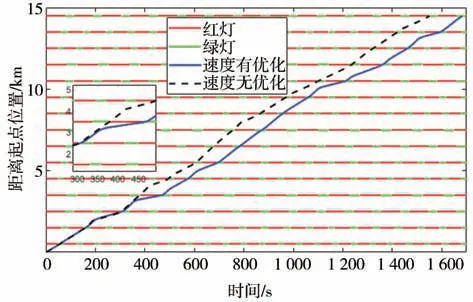
图8 不同策略下的车辆位置轨迹

图9 和图10 为两种策略下的速度与加速度轨迹。由图可知，所提策略优化后的速度变化平缓，且最大行驶速度为14.5 m/s，没有达到道路允许的最大速度约束，而没有速度优化的策略最大行驶速度为15 m/s，达到了道路速度约束，二者的平均行驶速度分别为8.613 8 和9.346 1 m/s，如表4 所示。所提策略车辆整体行驶较慢，这导致了行驶时间的不同，两种策略下的行驶时间分别为1 683 和1 551 s。尽管所提策略行驶时间较长，但安全性较高，且驾驶舒适性得到了提高，如表中所示，所提策略优化后的车辆加速度均方根误差（root mean square error，RMSE）为0.202 2，而没有速度优化策略的加速度RMSE 为0.839 8，对比可知所提策略的驾驶舒适性提升了75.92%。

图9 不同策略下车辆速度轨迹

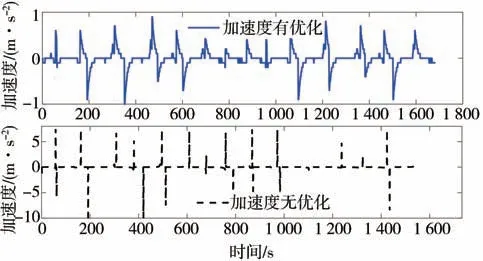
图10 不同策略下车辆加速度轨迹

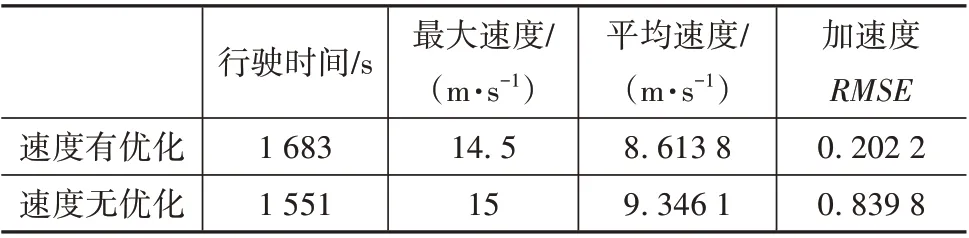
表4 两种速度规划策略结果

4.2 能量管理结果分析

为验证所提策略在燃油经济性方面的有效性，在中层控制中采用了另外两种基于线性SOC规划的方法，分别为基于行驶时间和行驶距离，则参考SOCref的计算方式如下。

线性规划1：

线性规划2：

式中：s（k）为k时刻行驶的路程；stot为起点到终点的距离；t（k）为k时刻行驶的时间；ttot为总的行驶时间；SOCmax和SOCmin分别为允许SOC的最大值和最小值。

图11 和图12 为3 种策略下发动机和电机的工作点图。由图可知，3 种策略下发动机和电机的工作点均表现出相似的结果，这是因为3 种策略下基于同一行驶工况的下层能量管理策略一致的结果。

图11 发动机工作点图

图12 电机工作点图

图13 为3 种策略下的SOC曲线，可以发现在前500 s 内3 种策略的SOC变化趋势基本相同，之后两种线性规划策略下SOC下降较快，而本文所提策略的SOC下降较慢，但在1 200 s 后本文所提策略SOC下降速度较另两种线性规划快。

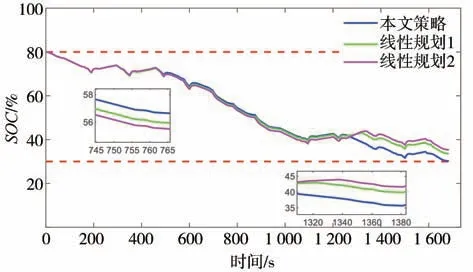
图13 3种策略下SOC曲线

3 种策略下的协态变量轨迹及燃油消耗情况如图14 与表5 所示。由图可知，本文所提策略的协态变量变化趋势相比于其他两种线性规划策略变化较为平缓，尤其在行驶后期，这种现象较为明显。此外，本文所提策略燃油消耗量为741.39 g，基于行驶路程和行驶时间的线性规划策略分别为800.55 和832.21 g。所提策略的燃油经济性相比于该两种策略分别提升了7.39%和10.91%，验证了其有效性，而线性规划1 的燃油经济性相比于线性规划2 提升了3.8%，这说明基于行驶距离的线性规划较基于行驶时间的经济性更合理。

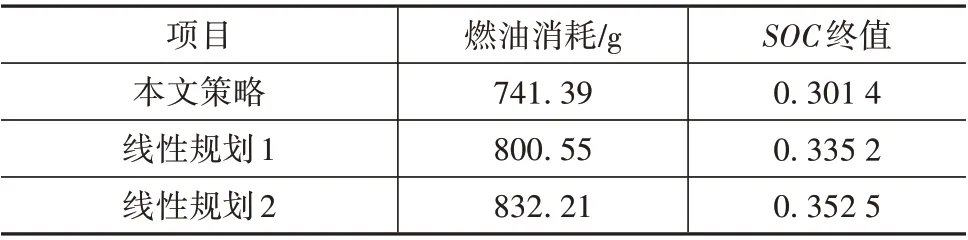
表5 3种策略下能量管理结果

图14 3种策略下协态变量轨迹

4.3 实验验证

为验证本文所提策略在工程应用的有效性，选取了如图15 所示的重庆市沙坪坝区大学城的两段真实道路交通模型作为本文实验对象［22］。

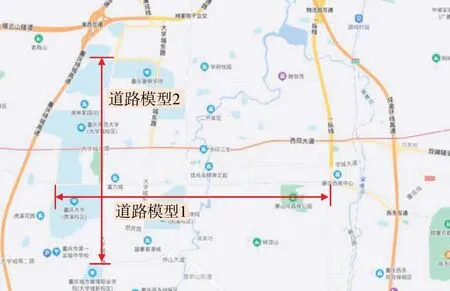
图15 实验道路对象

图中道路1 长度8.36 km，交通信号灯有13 个，道路2 长度8.3 km，交通信号灯11 个。本实验假设车辆先在道路1 上行驶，然后在道路2 上继续行驶，其中道路变换长度假设为500 m，因此可以建立如图16所示的道路交通信号灯模型。

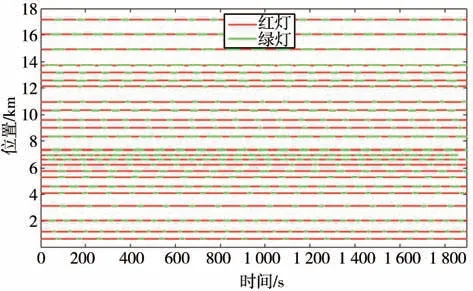
图16 真实道路交通模型

本文所提策略优化后的车辆位置轨迹及速度曲线如图17和图18所示，车辆可以在所有信号灯的绿灯周期内通过道路交叉口，验证了在该方法实际行驶中的有效性。此外，实验结果表明，燃油消耗为904.46 g，行驶时间为1 852 s。

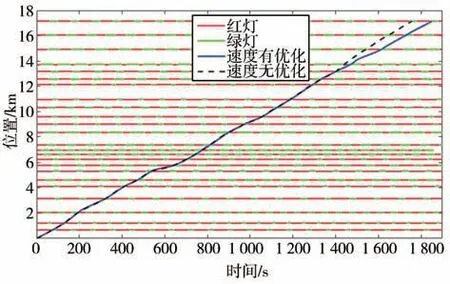
图17 车辆位置轨迹

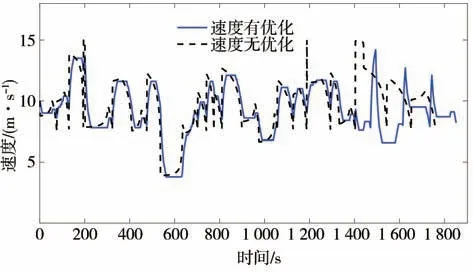
图18 车辆速度轨迹

5 结论

为提升插电式混合动力汽车在智能交通系统中的驾驶性能，本文基于分层解耦控制思想，设计了一种融合动态交通信号灯信息的分层式控制策略，解决了PHEV 在生态驾驶控制中算法计算效率与求解精度无法兼顾的问题，实现了车辆驾驶舒适性、燃油经济性的提升。本文主要研究结果总结如下。

（1）所设计的算法可以保证车辆顺利通过所有道路交叉口，避免了停车等待造成的燃油消耗，提高了燃油经济性。此外，与没有对车辆速度优化的策略相比，速度与加速的均方根误差有明显的降低，驾驶舒适性提升了75.92%。

（2）与基于行驶距离和时间的两种线性SOC规划策略相比，本文构建的分层式控制策略的燃油经济性分别提升了7.39%和10.91%。此外，仿真结果还表明基于行驶距离线性SOC规划的策略燃油消耗较基于行驶时间规划的要少。

（3）本文实验选取了两段长度共计17.16 km，信号灯数量为24 个的真实道路模型，结果显示在本文所提方法优化下，车辆在所有道路交叉口均可以在绿灯窗口内通行，且燃油消耗量为904.46 g，行驶时间为1 852 s，实验结果证明了所提方法的有效性。

未来的研究可以探索上层控制中信息安全性和不确定性，设计一种鲁棒性更好的控制算法，还可以考虑车辆行驶过程中的干扰，并与短期速度预测算法相结合，探讨交通信号灯位置、相位及周期变化对车辆驾驶风格及驾驶性能的影响，提高算法的工程应用性。此外，在下层控制中，可以使用其他算法对协态变量进行校正，进一步提高燃油经济性。