汽车永磁同步电机切换函数式混合控制策略

吴志恒，刘爱民

（沈阳工业大学电气工程学院，沈阳 110000）

前言

永磁同步电机及其控制系统具有效率高、控制精度高、转矩密度大、转矩平稳性好和振动噪声低等特点［1］，在电动汽车领域应用广泛。

电动汽车所配永磁同步电机（permanent magnet synchronous motor，PMSM），其工作环境复杂，需频繁启动，大幅加减速，同时考虑续航里程因素，就需其控制系统具有系统效率高、适应能力强的特点［2］。高性能的控制策略应用于电机控制系统，可使电机的各种潜在能力得到充分发挥，使电机的工作性能更符合使用要求。因此，许多国内外学者对电动汽车的驱动控制系统进行了大量研究。

目前，车用PMSM 及其控制策略呈多样化、智能化。文献［3］中提出一种电动车用多盘式永磁同步电机协同优化与容错控制方法，能提高系统效率且具有很好的可靠性。文献［4］中提出基于模糊自适应速度调节器的绕组切换型电机控制方法，解决了双绕组切换型电机在绕组串联和并联时切换过程中速度波动抑制等问题。文献［5］中提出了一种新型永磁同步电机MT 坐标系下直接转矩控制系统，解决了直接转矩驱动技术在电动汽车动力系统应用中存在的低速转矩脉动和该动力系统对恒功率调速范围要求较高的问题。文献［6］中提出一种粒子群优化模糊控制器（particle swarm optimization fuzzy logical controller，PFC），能够满足电动汽车负载变化以及高速度的要求。文献［7］中提出了一种基于Hamilton 系统H∞控制理论的扰动抑制算法，较好地解决了PMSM 驱动系统在实际工况中存在的负载扰动问题。文献［8］～文献［13］中也都针对电动汽车电机运行过程不同方面的性能优化提出了有效的控制算法。以上均是针对特定结构的PMSM 或优化驱动电机在电动汽车应用环境中的某一性能及解决某一问题的控制算法研究。但特殊结构电机基本处于探索阶段，其控制方法专用性较强，未能推广使用；优化驱动电机控制某一性能的智能控制算法，具有复杂性高、计算量大和对内存需求高的缺点。

智能算法仅在瞬态条件下性能优越，而PID 控制算法在稳态条件下性能优越。将模糊PID 算法和常规PID 控制算法通过切换函数进行结合可获得这两种控制算法的综合优点。为减少控制器的计算负担和执行时间，易于工程化实现，提出采用具有模糊PID 算法瞬态性能的模糊比例算法代替模糊算法。同时为提高PID 控制算法的响应速度，推导其反馈原理，提出改进PID 算法代替常规PID 控制算法。考虑使用一组规则或一个单独的模糊算法来确定两个控制算法输出的权重，则需要一个额外的模糊计算、更多的计算时间、更多的增益常数调整。增加的计算量会降低控制系统开关频率，导致较高的转矩波动，本文提出切换函数式混合控制策略（switch the functional hybrid control strategy，SFHCS），设计切换函数计算输出权重控制两者输出占比。最后，通过仿真与实验，验证了车用PMSM 采用所提控制策略系统有效性。

1 车用永磁同步电机

作为电动汽车的驱动部分，电机类型及其控制方法直接决定了电动汽车的动力性［14］。对于电动汽车轻载和低速时系统效率较低，提高续航里程须扩大高效运行范围等问题，从控制策略和电机本体两方面寻找有效和可靠的方法［15］。

相比于异步电机、无刷直流电机等常用电机，PMSM 具有高效运行范围宽、系统效率高、功率密度大等优点，被广泛应用于电动汽车驱动系统。因此本文中以PMSM 为研究对象，探讨其控制算法，提高其控制输出性能，对行业发展具有重要意义。所研究的PMSM 结构如图1 所示，电机具体参数如表1所示。

图1 PMSM的定转子结构图

表1 PMSM 样机参数

2 切换函数式混合控制策略

电动汽车行驶在城市道路上，其驱动电机经常处于启动、加速、恒速、减速等多种工作状态，并伴随各种干扰［16］。单一控制算法很难满足各个工作状态的最优控制要求。多种算法综合控制是电动汽车驱动系统的发展趋势。

2.1 改进PID控制算法

控制系统的基本作用是将被控变量与参考输入进行比较，根据误差情况作出决策，控制算法对误差的运算处理决定控制系统的性能。电机控制系统须对变化的工作环境具有快速响应和抗干扰能力。分析常规比例、积分、微分控制算法，其系统如图2所示。

图2 PID控制系统框图

根据图3 可知，在前馈回路中每增加一种对误差的运算，同时增加了对参考输入和被控变量的运算，对参考输入的每一种运算都将在整个控制系统的微分方程中表现出来，如式（1）所示：

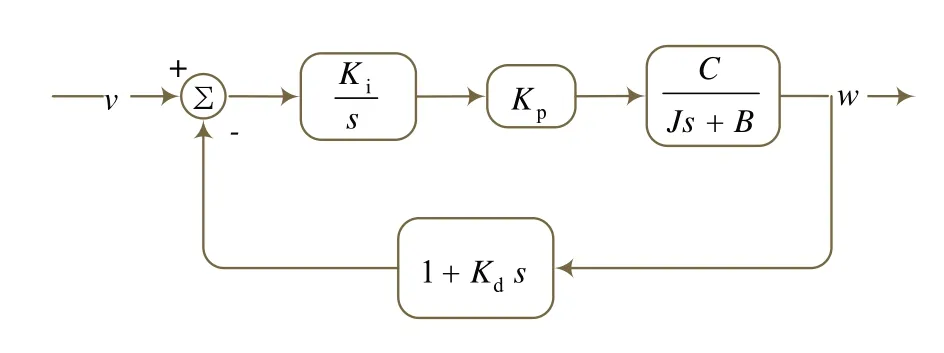
图3 优化PID控制系统框图

使输出不能紧跟输入量的变化，还随输入量的积分和微分变化。

根据分析，控制系统的前馈回路中只能采用积分运算，但为保证系统的快速性、稳定性等理想的控制特性，须提供被控对象的微分量。为避免引入参考输入的微分量，出于补偿目的被控量的微分须全部在反馈回路中。根据以上分析，设计控制系统，其框图如图4所示。

微分方程为

从图4 可以看出，对输出信号微分的积分仍是w（t），这就说明没有必要对w（t）进行微分。在工程上应尽量回避微分运算，可以将图3 的控制系统改成图4的控制系统。

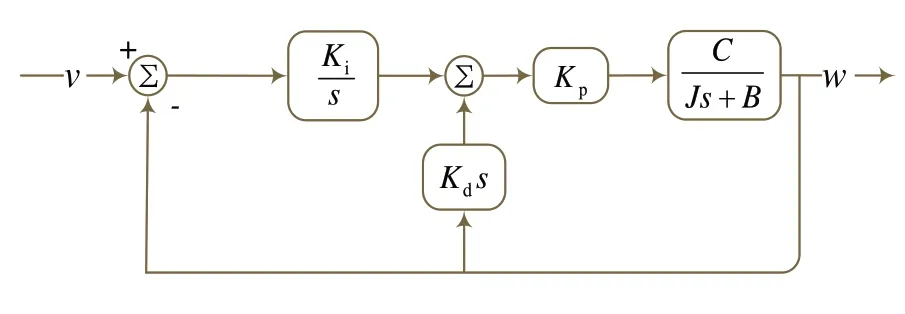
图4 避免微分的控制系统框图

其微分方程仍为

由图4 可知，控制系统的前向回路中只有一种运算，即对误差只能采用积分运算。这样既能保证电机速度的静态误差为零，又减少系统微分方程的运算项。前向回路中只采用积分控制器有利于提高系统的控制精度，但在克服误差的过程中系统可能出现振荡甚至发散等问题，不利于系统稳定。为确保系统的稳定性，在反馈回路中对电机速度进行微分运算，微分运算能够预测电机的速度变化趋势，增加系统的阻尼程度，减小系统的超调和振荡。同时，由式（4）可看出，没有对被控变量直接进行微分，得到与微分完全相同的结果，可以保证系统具有快速跟随性，改善常规PID控制算法的控制性能。

建立PMSM 双闭环控制系统，采用改进PID 控制算法代替常规PID 控制算法。改进后PID 控制算法具有优越的控制性能，但其控制参数固定，当系统出现干扰时，参数无法根据当前环境进行改变，其控制性能会下降。为解决此问题，在环境变化大的情况下，采用模糊比例控制算法。

2.2 模糊比例控制算法

模糊控制是一种自由形式的数学建模，基于使用系统的经验形成的语言规则。模糊PID 参数整定有偏差E和偏差变化率EC两个输入量；有参数ΔKp、ΔKi、ΔKd3 个输出量。模糊PID 控制算法须设在偏差论域E和偏差变化论域EC及参数ΔKp、ΔKi、ΔKd上，分别定义7个模糊子集PL（正大）、PM（正中）、PS（正小）、ZE（零）、NS（负小）、NM（负中）、NL（负大），采用归一化论域。

考虑模糊PID 控制算法其参数整定涉及近似值、复杂性高、计算量大，且仅在瞬态性能优越。根据模糊速度控制器的输出可知，在瞬态开始时，其值接近最大允许的输出值，且随速度误差的减小而减小。

为进一步减小模糊PID 算法的计算量，提出采用模糊比例控制器代替模糊PID 控制算法。模糊比例控制器是一个比例调节控制器，其增益调节是在限制器的约束下实现，模糊比例控制器的输出与瞬态开始时模糊控制器的输出相当。模糊比例算法复制了模糊算法在瞬态条件下的性能，能够保证电机控制系统的输出速度响应能力。模糊比例控制器方程为

式中：Q（t）是模糊比例控制器输出；E（t）是误差；Ke是增益常数。

混合控制中只有在速度大幅变化时，才启用较大占比的速度模糊比例控制器，此时其积分、微分环节几乎不起作用，为进一步减少计算量，简化系统，对模糊PID 控制器进行裁剪。使用模糊比例算法代替模糊PID 控制算法，减少系统计算量，可保证其具有稳定性和快速性。

2.3 切换函数的建立

改进PID 控制算法能够在没有对被控变量直接进行微分的情况下，得到与微分完全相同的结果，具有快速跟随性。在电动汽车恒速运行过程中，环境变化小的情况下，能够快速响应，调整输出，保证整车的稳态运行性能，增强驾驶舒适性。

模糊比例控制算法能够复制模糊PID 算法在瞬态条件下的性能，在启动、大幅加减速及有外部干扰时，能够准确、快速调节输出，保证整车的瞬态运行性能。

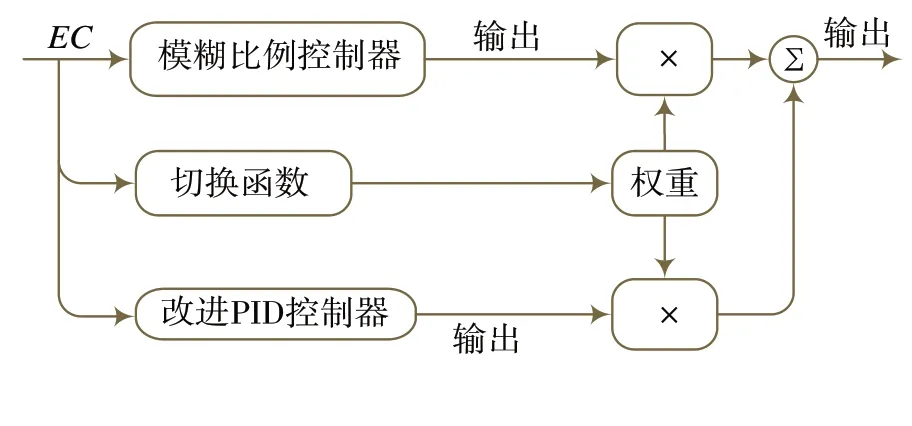
图5 SFHCS原理框图

SFHCS控制技术的关键是切换函数的建立。切换函数主要实现两个控制器输出占比分配，即权重的计算。

本设计所控制驱动电机不考虑弱磁升速，其速度范围在0～3 500 r/min，故其速度偏差E也在0～3 500 r/min 范围内，将其量化在［0，1］域内。当偏差E越接近1时，说明速度偏差越大，速度需大幅调整，此时须控制模糊比例控制器输出占比增加；当偏差E越接近0时，说明速度偏差较小，速度需微调，电机运行在稳态，此时须控制改进PID 控制器输出占比增加；根据速度偏差值所需控制模糊比例控制器输出占比进行实验摸底，绘制模糊比例控制输出权重与误差的曲线，如图6所示，并总结得出式（6）。

图6 输出权重与速度偏差的关系曲线

图中X轴为速度偏差，Y轴为模糊比例控制器的输出权重。设定模糊比例控制算法的输出权重为f（x），则改进PID 控制算法的输出权重为1-f（x）。根据绘制的曲线，建立切换函数为

在实际操作过程中，当偏差大于90%时，工况变化较大，需大幅调整速度跟随给定，故只须控制模糊比例控制输出，让其快速调整；当偏差小于10%时，偏差较小，电机处于稳定输出，故只须控制PID控制输出即可。本文设定a=0.1，b=0.9。速度控制器输出函数为

式中：y为速度控制器输出；y1为模糊比例控制算法下的输出；y2为改进PID控制算法下的输出。

3 仿真与实验结果分析

3.1 仿真模型建立

为验证所提控制策略的有效性，建立PMSM 切换函数式伪微分反馈控制系统仿真模型，如图7 所示。仿真模拟电动汽车运行工况，分别从动态响应特性、抗干扰能力及效率3 个方面，对比分析了所提控制策略与常规控制策略。本文所研究的PMSM 参数见表1。

研究发现，黑水虻幼虫能够分泌己二酸，欧美许多国家利用己二酸较强的广谱抗菌能力，将黑水虻幼虫用于皮肤损伤(如烧伤和创伤愈合等)的临床处理，当己二酸浓度达到120 μg/ml时，可以有效抑制痢疾和耐甲氧西林金黄色葡萄球菌等的生长[2]。Choi等从黑水虻幼虫体内直接提取分离出己二酸，可有效抑制革兰氏阴性菌(如肺炎克雷伯菌、淋病奈瑟菌、宋内志贺菌等)的活性[23]。

图7 SFHCS仿真模型

3.1.1 动态响应特性分析

电动汽车驱动系统的动态响应特性，直接影响整车启动、速度提升等方面能力。其主要反映在系统响应速度、调整时间、超调量等方面。本文考虑电动汽车的启动和加速运行工况，选取启动过程转速及转矩的响应特性进行仿真分析，仿真结果如图8所示。

从图8（a）可知，SFHCS控制下，转速上升到给定值的调节时间为0.021 s，无超调；常规PID 控制下，转速上升到给定值的调节时间为0.039 s。超调量为2.25%，稳定时间为0.14 s。因此采用SFHCS 控制策略，车辆启动时其加速更快且平稳。

从图8（b）可知，恒定转速下加载转矩，SFHCS控制下，转矩达到给定值的调节时间为0.06 s，达到给定转矩后，无超调；常规PID 控制下，转矩达到给定值调节时间为0.036 s，超调量为281.2%，稳定时间0.2 s。由数据分析可知，采用SFHCS 控制策略，在车辆运行加载时，其输出转矩响应更快且无抖动。

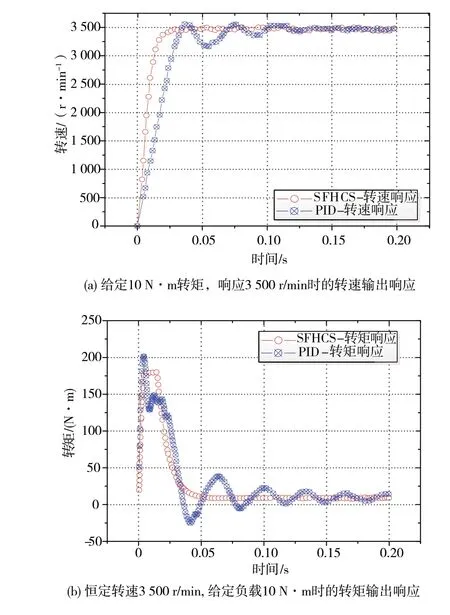
图8 两种控制策略下的输出响应曲线

3.1.2 抗干扰能力分析

电动汽车驱动电机及其控制系统在实际运行过程中，会存在一定的外在干扰，导致电机输出产生波动，波动大小因干扰产生的偏差值而定。根据控制要求，控制器须输出相应能量消除偏差，在同样的干扰情况下，具有抗干扰能力的控制器引起的输出波动小，能够节省输出能量。同时，能够保证电动汽车运行过程的稳定。图9 为干扰情况下，SFHCS 与常规PID控制算法抗干扰的输出能力对比。

图9（a）为恒定转矩，在0.1 s 时刻突加转速干扰，SFHCS 控制下，转矩的超调量为1.67%，恢复时间为2 ms；PID 控制下，转矩的超调量为9.33%，恢复时间为30 ms。图9（b）为恒定转速，在0.1s 时刻突加转矩干扰，SFHCS 控制下，转速的超调量为3.77%，恢复时间为23 ms；PID 控制下，转速的超调量为6.73%，恢复时间为89 ms。通过转矩和转速抗干扰仿真数据对比分析，SFHCS 控制策略具有较好的抗干扰能力，电动汽车驱动电机采用SFHCS 控制策略，在车辆运行过程中应对突变干扰时，更具稳定性。

3.1.3 电机效率分析

PMSM 效率取决于电机的本体及其控制器。电机本体确定情况下，其控制器不同的控制性能可能会导致不同的电机效率。通过对电机控制器中SFHCS 和PID 两种控制策略的应用比较，以验证SFHCS控制策略在动态过程中具有对电机工作效率进一步提升的能力。

由图10 可知：在动态响应过程中，SFHCS 控制下驱动电机在20.1 ms后效率达到90%以上；PID 控制下驱动电机在启动过程中开始出现抖动，导致效率计算结果出现先增后减再增的趋势，其在31.6 ms后效率达到90%以上。对比分析，SFHCS 控制策略下电机可提前达到高效区，对电动车辆运行的效率提升及进一步增加续航里程具有一定意义。

图10 两种控制策略下电机效率曲线

3.2 实验验证

为验证SFHCS 控制策略在实际应用中的有效性，本文搭建以DSP28335 为核心的控制系统，建立电机及其控制系统对拖测试平台，如图11 所示。前期通过对拖平台模拟电动汽车运行工况进行验证。为后续在实际路况下进行电动汽车整车运行实验提供数据支撑。

图11 测试平台

电动汽车一般采用转矩控制，通过输出转矩来达到提升电动汽车的转速。实验电压为380 V，转速上限为3 500 r/min。为模拟电动汽车运行工况，给定电机10 N·m 的转矩，并限定上限转速3 500 r/min，考察电机的转速响应能力，实验数据曲线如图12所示。

图12 转速输出响应曲线

分析图12 可知：SFHCS 控制下电机达到最大转速时间为22.3 ms，无超调；常规PID 控制下电机达到最大转速时间为26.6 ms，超调量为12.1%，达到稳定的时间为66.7 ms。SFHCS 控制策略较常规控制策略能使电动汽车启动过程更快、更稳。

在上述实验条件下，160 ms时施加转矩干扰，将转矩由10突变至20 N·m，验证控制系统的抗干扰能力，实验结果曲线如图13所示。

由图13 可知：SFHCS 控制下，转速超调量为2.91%，恢复稳定时间为27 ms；常规PID 控制下转速超调量为7.85%，恢复稳定时间为32 ms。实验验证，SFHCS 控制策略具有更好的抗干扰能力和快速恢复能力。电动汽车采用该控制策略在增强驾驶稳定性基础上可减少能量输出，提高效率。

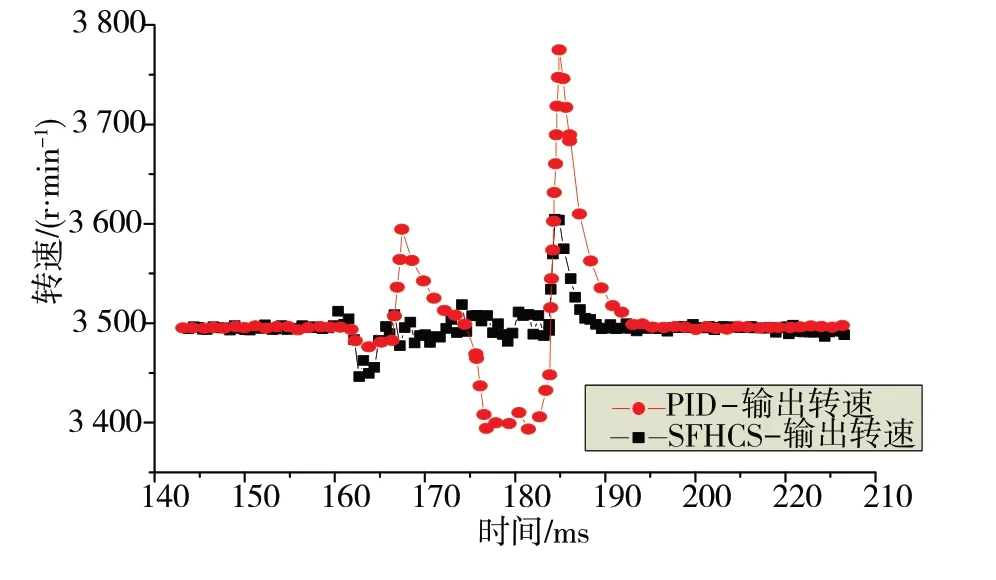
图13 干扰下转速输出曲线

为进一步验证所提控制策略具有提高整车工作效率的能力，在额定转矩和不同转速下，对比分析了SFHCS 控制策略和常规PID 控制策略下的电机输出效率。受平台限制，验证至转速4 000 r/min。实验结果如图14所示。

图14 不同转速下效率曲线

从图14 可以看出，采用SFHCS 控制策略，电机各个转速点上效率均有所提高，额定转速3 500 r/min时，功率提升达2.1%，达到额定转速后各转速点的效率略有下降。但SFHCS 控制策略下的电机效率始终高于PID 控制策略下的电机效率。故采用本文所提的控制策略，能够有效提升电机的运行效率。

4 结论

首先建立电动汽车PMSM 的数学模型及双闭环控制系统，提出了控制系统采用SFHCS 控制策略。通过切换函数分配权重值将模糊比例控制器与伪微分控制器融合，获取两个控制算法的优点。搭建SFHCS 控制系统仿真模型，从响应速度、抗干扰能力、效率提升等方面验证所提控制策略的有效性。通过实验平台模拟电动汽车驱动电机实际工况进行实验验证，结果表明所提控制技术能够提升电动汽车驱动系统工作效率，增强运动过程的平稳性及响应速度，主要结论如下。

（1）电动汽车驱动电机采用SFHCS 控制策略相比于常规PID控制策略，其启动时间缩短了44.4 ms，且无超调。

（2）电动汽车驱动电机采用SFHCS 控制策略在应对突发干扰情况时恢复稳定时间为27 ms，相比于常规PID 控制策略缩短了5 ms，且超调量减少了4.94%。

（3）采用SFHCS 控制策略，电机各转速点上效率均有所提高，额定转速3 500 r/min 时，功率提升达2.1%。

由于条件限制，所提控制策略未能在实际车辆运行中进行实验验证。因此，在未来工作中将考虑根据车辆实际运行情况及反馈数据，进一步对各阶段所需控制算法和切换函数进行优化。