基于轨迹预测的智能汽车行驶风险评估方法 *

高 翔，陈 龙，王歆叶，熊晓夏，李祎承，陈月霞

（1.江苏大学汽车工程研究院，镇江 212013；2.江苏大学汽车与交通工程学院，镇江 212013）

前言

行车风险评估是驾驶辅助系统和智能汽车安全运行的重要基础。近年来，随着智能交通系统（ITS）的迅速发展，大量驾驶安全技术已被应用于高级驾驶辅助系统（ADAS）和自动驾驶汽车（AVs）［1-3］，如采用基于安全距离、碰撞时间或所需减速度的碰撞预警参数［4-7］来实时评估车辆的行驶安全状态。然而这些预警参数主要基于自车和前车的距离、速度、加速度等当前运动状态信息，无法反映驾驶员行为特征、车辆状态与道路环境之间的相互作用，因此难以为车辆安全决策提供准确的判断依据。

随着智能感知和通信技术的发展，可以获取的车辆实时运动和环境特征信息更加丰富，行车风险评估方法亦更加多元化，目前主要包括基于碰撞概率、基于行车风险场以及基于机器学习的方法。概率方法通常利用车辆之间的时间和空间关系以及输入数据的不确定性，利用概率描述来建模风险水平。Noh 等［8］利用位置不确定性和基于距离的安全度量提出了一种基于贝叶斯网络的行车风险概率模型。Bahram 等［9］将时空成本图与贝叶斯网络相结合，在驾驶员意图预测的基础上，从制动减速度的角度构建前后相邻车辆的碰撞概率。行车风险场是指在实时获取车辆周边道路交通信息的基础上，建立类比“物理场”的数学模型来定量描述车辆所面临的行车风险。Wang［10］等提出了行车风险场理论用于评估交通场景中包含多要素的动态风险，为驾驶过程中影响驾驶安全的“人-车-路-环境”要素构建了统一模型。田野等［11］提出了一种行车风险场的扩展模型，将碰撞时间（TTC）融入风险场模型，同时引入车辆几何特性和航向角信息来扩展模型的适用性。机器学习方法通常将交通安全影响因素的各项具体指标值作为输入变量，交通安全评估等级作为输出变量。Lee 等［12］构建了多层感知器神经网络MPNN 对行车风险程度进行实时估算。Fu 等［13］综合考虑行驶安全和舒适性两个方面构建了基于神经网络模型的风险等级划分算法。

然而，以上模型方法仍具有一定局限性。基于碰撞概率的方法通常只考虑自车与前车之间的不确定关系，忽略了周边多车行为或运动的相互影响。基于行车风险场的方法大多基于当前车辆的相对位置进行计算，而在实际快速行车过程中即使在短时间内位置也可能发生很大变化，不利于后续构建准确的避撞控制方案。基于机器学习的方法普遍没有考虑实际行车过程中需要面对的周边多车复杂场景下的多车间碰撞风险问题，影响了此类算法在现实中的实用性。综上所述，目前主要的风险估计方法仍难以适应实际行车场景的复杂性和不确定性特点。

针以上问题，本文在周边车辆预测轨迹基础上，采用考虑驾驶员行为不确定性的驾驶风险域（driver’s risk field，DRF）作为风险概率度量，综合考虑对车辆安全有较大影响的环境事件成本作为严重程度度量，得到适应复杂行车场景不确定性的量化感知风险；根据实车轨迹数据，基于贝叶斯理论的量化感知风险等级概率，对预测区间内所有时刻的量化感知风险进行加权融合，最终实现对未来行车潜在碰撞风险的预测。风险评估总体流程如图1 所示。其中，由于本文主要关注风险建模方法而非轨迹预测，文中自车周边车辆轨迹采用文献［14］中的基于自车与周边环境交互信息的环境注意力网络（environment-attention network，EA-Net）模型进行预测。该模型为了更好地捕获车辆在行驶过程中与周围环境各节点连边更新特征及空间位置结构特征信息，在LSTM encoder-decoder 与卷积社交池串联的结构基础上，加入了图注意神经网络和包含SE 模块的卷积社交池组成并行结构，提高了环境交互信息的提取效果，达到了较好的轨迹预测水平。

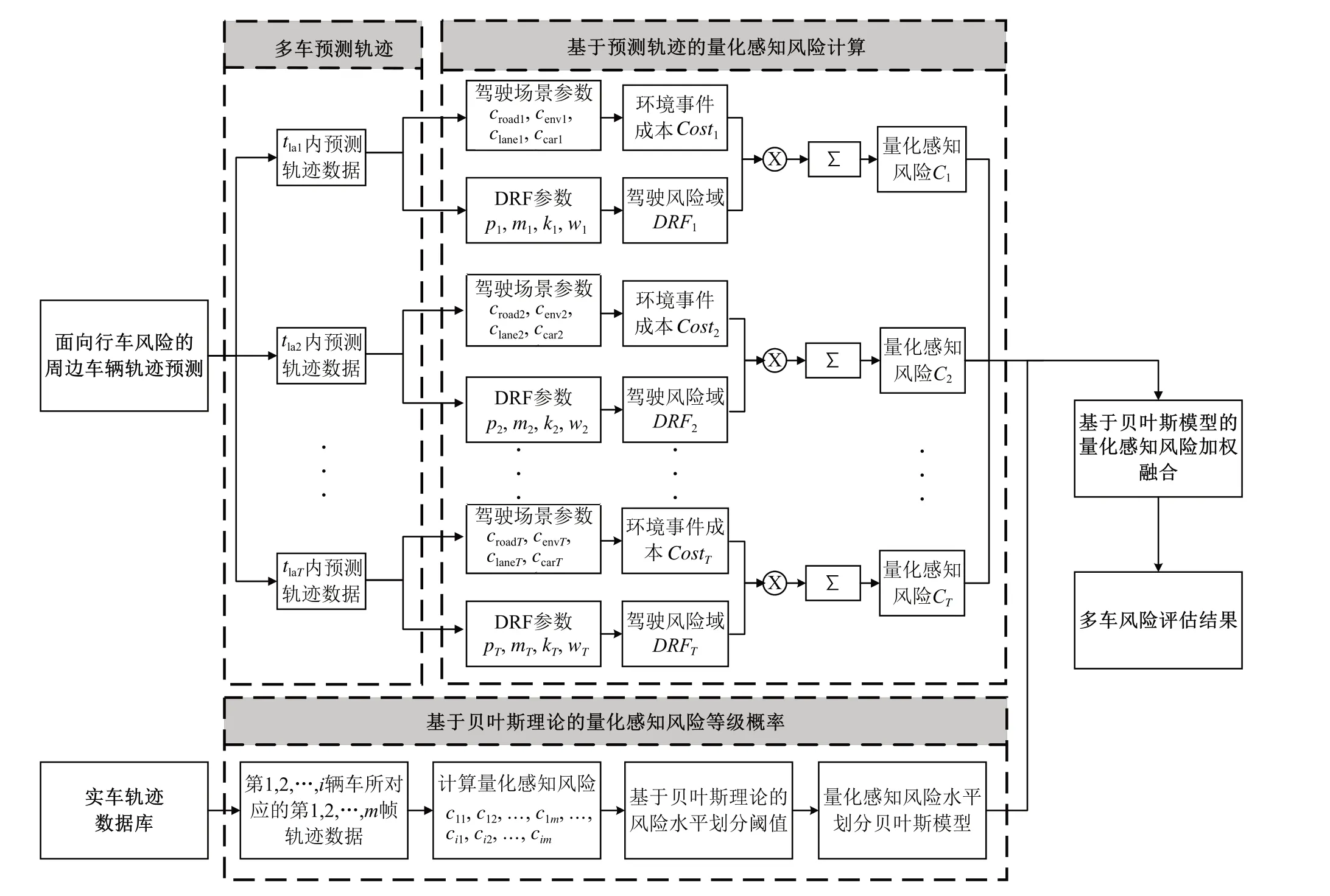
图1 基于轨迹预测的行车风险评估总体流程图

1 基于预测轨迹的量化感知风险

本文中量化感知风险是表征风险概率度量的驾驶风险域与表征严重程度度量的事件成本的乘积。其中，驾驶风险域DRF是在车辆预测轨迹的基础上，结合驾驶员感知风险后采取行为的不确定性，在预测时间内出现在某一空间位置的概率量化值；事件成本是驾驶场景中静态或动态障碍物在预测时间内的预测位置上与车辆发生潜在风险后果的严重程度。

量化感知风险示意图如图2 所示。图中：黑色圆点代表当前时刻自车位置；事件成本图中蓝色立方体代表周边其他车辆相对于自车所产生的风险成本Ccar，绿色立方体代表自车车道边界外的成本Cenv，黄色立方体表示车道线成本Clane；驾驶风险域图显示了DRF在车辆预测轨迹附近的高低变化；星号*代表将行车周边范围内各个网格点上的事件成本与DRF相乘，得到量化感知风险分布图。对所有网格点上的量化感知风险求和，即得到驾驶员行车周边范围内的总量化感知风险（为一标量值）。本文以自车视角构建驾驶风险域DRF，对于自车为人工驾驶的车辆，其预测轨迹可以通过基于环境交互信息的周边多车轨迹预测模型［14］实时输出；对于未来自车为自动驾驶的车辆，其预测轨迹可设置为车辆自主规划轨迹。

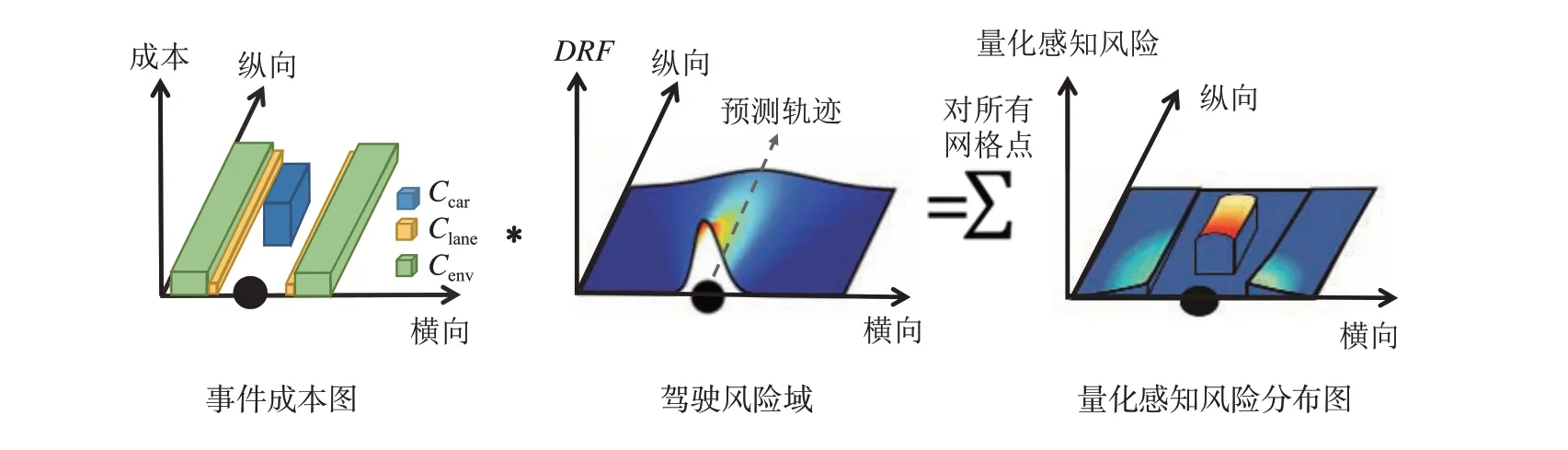
图2 量化感知风险示意图

1.1 DRF模型构建

假设DRF分布为一个沿着预测轨迹延伸的且具有高斯截面的曲面，可以构建前瞻时间tla内车辆驾驶风险域DRF模型［15］，即

式中：a和σ分别代表高斯分布的高度和宽度；（x，y）为行车周边范围内各个网格点坐标；（xc，yc）为（x，y）至车辆预测轨迹的垂点坐标；d为网格点（x，y）到预测轨迹垂点（xc，yc）的距离，如图3 所示。可以看出，驾驶风险域DRF在车辆预测轨迹附近具有较高的值，并且随着与初始时刻车辆位置（xv，yv）的横向和纵向距离的增加而减少，从而反映了驾驶员在感知和行动中的不确定性。

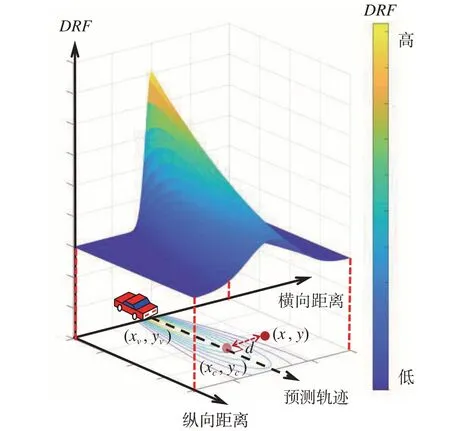
图3 量化感知风险示意图

其中，高斯截面的高度a为一条关于距离初始位置（xv，yv）累计行驶路径长度L的抛物线：

式中：p定义了抛物线的陡度；s为前瞻时间tla内车辆预测轨迹总路径长度。

高斯截面的宽度σ亦为关于累计行驶路径长度L的线性函数：

式中：w为车辆宽度修正参数，可取为车辆宽度的1/4；m定义了高斯截面的扩大（或缩小）的斜率；δ代表了车辆转向角；k表示DRF模型的边缘参数。综上，驾驶风险域DRF可由4 个参数（p，m，k，w）定义，除了车辆宽度修正参数w外，其他参数p、m、k均可根据驾驶员风险感知特性由网格搜索算法进行估计。本文根据实验结果［15］，p取0.006 4，m取0.001，k取0.69。

为了量化车辆后方范围内动态障碍物可能带来的风险，本文以自车质心位置的横断面为对称面，向后建立了一个与前方DRF对称的风险域，从而实现对车辆周边范围量化感知风险的连续刻画。

1.2 环境事件成本定义

环境事件成本定义了车辆与周围静态、动态障碍物处于特定状态的风险后果，行车周边范围内环境事件成本的确定方法如下：

式中：ccar、clane和cenv分别代表动态障碍物（障碍车辆，即周边行驶车辆）、车道线和车道外成本；θ1、θ2和θ3分别为环境事件类型的0-1 判别函数。对于动态障碍物形成的成本，本文不考虑障碍车辆尺寸，当自车与相邻障碍车辆形成跟车场景或插车场景时，障碍车辆成本用两车间距离Δd和速度差Δv来表示，记作ccar1；其他驾驶场景中障碍车成本固定为1 200，记作ccar2。由于本文主要考虑的风险为周边障碍车与自车之间的动态风险，所以对静态障碍物设置较低的事件成本值，假设车道线成本（clane）为10，车道边界外成本（cenv）为500，如表1所示。

表1 环境事件成本参数

环境事件成本的空间分布随周边车辆预测轨迹结果动态变化，如图4 所示，黑色圆点和深色立方体分别表示自车和前方障碍车的初始位置（t0），灰色圆点和浅色立方体分别表示它们在下一时刻（t1）的预测位置，两圆点间的连线（黑色虚线）表示自车预测轨迹，两立方体间的连线（蓝色虚线）表示障碍车预测轨迹。对于初始时刻自车形成的行车风险域为DRF0，障碍车对其构成的动态事件成本ccar0由深色立方体所示；对于下一时刻自车形成的行车风险域为DRF1，障碍车对其构成的动态事件成本ccar1变为浅色立方体所示。可以看出，驾驶风险域DRF与驾驶场景中的事件成本均随着预测时间的推移实时变化，可以动态反映驾驶员感知风险和驾驶行为变化的后果，从而实现对于未来行车潜在碰撞风险的实时刻画。

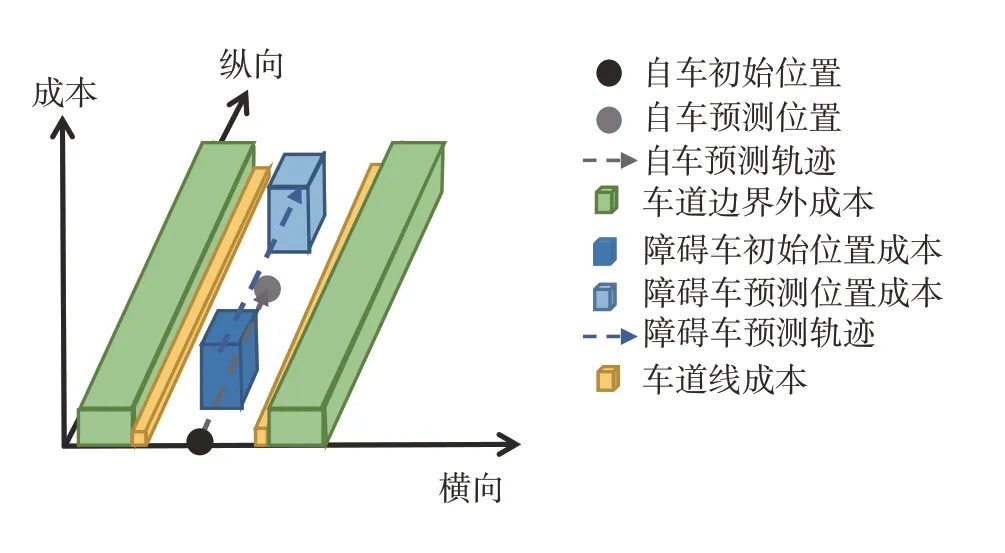
图4 事件成本动态示意图

1.3 量化感知风险计算

根据预测区间内自车预测轨迹构建的驾驶风险域DRF，结合周边车辆行驶轨迹预测结果，将DRF与对应位置环境事件成本相乘得到量化感知风险。采用移动时间窗形式将预测区间均匀划分为T段{tla1，tla2，…，tlaT}（如图5 所示），并将其视为自车的T段前瞻时间。当以周边第i辆车作为障碍车辆时，自车前瞻时间tla，m(m= 1，2，…，T) 内的量化感知风险为

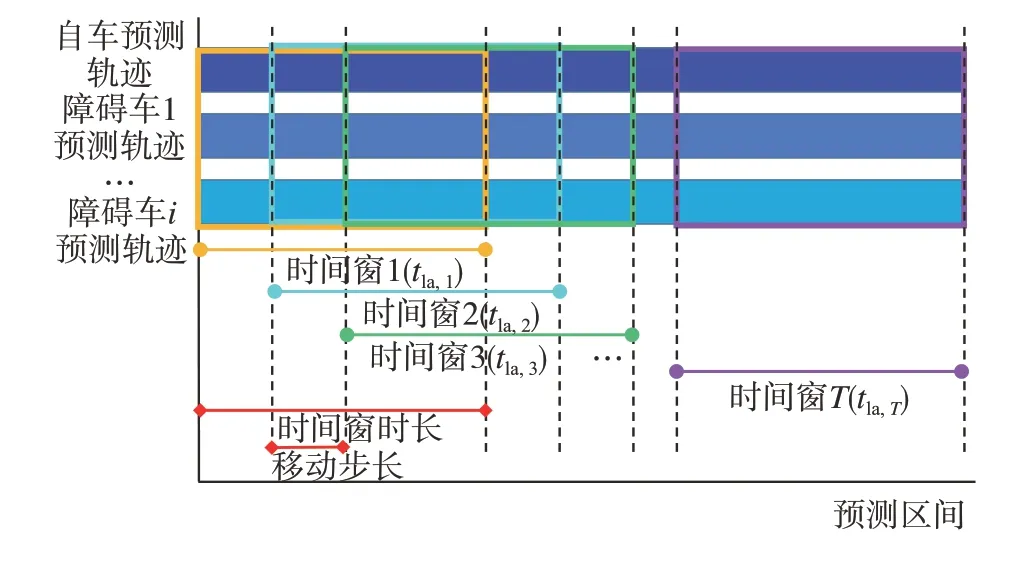
图5 预测区间移动时间窗划分

式中：DRFm为前瞻时间tla，m内自车的驾驶风险域（式（1）～式（4））；cim为对应时间的环境事件成本（式（5）～式（8）），其中动态障碍物定义为车辆i；(x，y) ∈S表示行车周边范围内所有网格点的坐标。

按式（9）对预测区间内的每段前瞻时间进行计算，得到预测区间内对应T个前瞻时间的量化感知风险时间序列值｛Ci1，Ci2，…，CiT｝。

2 基于贝叶斯模型的融合感知风险

在上一节划分的多个移动时间窗的基础上，本节基于贝叶斯理论将每个时间窗内的量化感知风险值转换为所处风险等级的概率，并对所有时间窗的风险等级进行概率融合计算，降低单个时间窗内轨迹预测误差可能对风险评估结果造成的影响。

2.1 基于贝叶斯模型的风险等级划分

与仅预测二元潜在风险（发生或不发生）的方法不同，本文将基于贝叶斯理论分别估计量化感知风险C处于高、中、低3 个风险等级的概率［1］，定义如下：

Ω ≝{dangerous，attentive，safe}≝{D，A，S}

Ω 是风险水平的集合，D、A、S分别表示危险、中等和安全等级，并分别赋予量化值2、1和0以描述风险水平，即将风险等级τ定义为

τ∈Ω ≝{2，1，0}

设高、低驾驶风险等级下量化感知风险C对应的阈值分别为TD和TS，中风险等级下C的期望值为TA，则可构建量化感知风险C的条件分布概率为

式中P(C|τ=a)，a∈Ω 表示在不同风险等级下观测到量化感知风险C的概率。具体以式（10）为例，其表示当驾驶状态处于高风险等级时，观测到量化感知风险值C大于高风险等级阈值TD的概率为1；观测到其他小于阈值TD的C的概率由C与TD的相对大小决定，C与TD越接近，则观测到该C值的概率越大。参数σ为不确定性因子，主要用于控制不同驾驶风险等级曲线的平滑度。根据贝叶斯理论，风险等级τ的后验概率为

式中：P（τ|C）表示给定量化感知风险C下车辆处于某一风险等级的概率；P（τ）为每个风险等级的先验概率，并满足约束∑τ∈ΩP(τ) = 1，文中假设不同风险等级具有相同的先验概率（均为1/3）。

文中预设参数TD、TA和TS可根据实车轨迹数据的分布特征确定。NGSIM 数据集是美国FHWA 采集的由摄像头获取的实际车辆行驶轨迹数据［16-17］，本文选择其中的US101和I-80高速公路轨迹数据用于此处参数标定和后文模型验证。随机选取NGSIM数据集中347 条（共计10 625 数据帧）实际车辆轨迹数据，按式（9）计算每帧前瞻时间tla内自车的量化感知风险（前瞻时间tla取0.2 s），得到的量化感知风险分布图如图6所示。

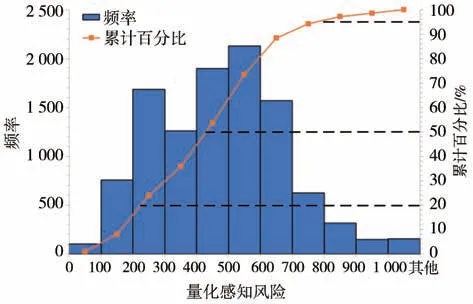
图6 实车轨迹量化感知风险统计分布图

考虑到实车轨迹数据样本中紧急工况较少，分别选取量化感知风险从小到大排序的95%和20%分位值作为高、低驾驶风险等级对应的阈值TD和TS，50%分位值作为中风险等级的期望值TA，即TD、TA和TS依次近似取值为800、500 和250。在此基础上，根据式（10）～式（13）计算得到量化感知风险C的条件分布概率如图7 所示。其中，为了获得具有合理分布的平滑风险曲线，文中不确定性因子σ经试验取120。

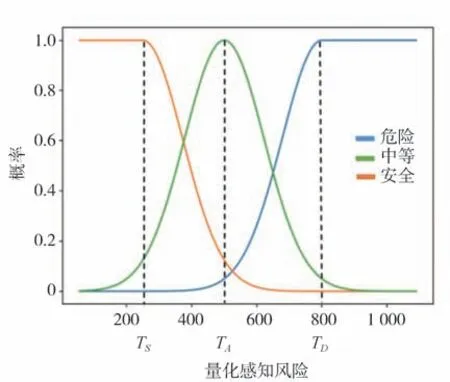
图7 量化感知风险的条件分布概率示意图

2.2 基于风险等级概率的融合感知风险

根据自车和周边车辆预测轨迹数据，基于量化感知风险计算公式和行车风险等级概率确定方法，对预测区间内的预测风险等级进行融合计算，具体按如下步骤计算驾驶场景的最终融合感知风险：

（1）筛选出自车周边的第1，2，…，i辆车作为旁车，分别记为CAR1，CAR2，…，CARi；

（2）分别计算预测区间中T段前瞻时间{tla1，tla2，…，tlaT}内当旁车CARi作为障碍车辆时对自车产生的预测量化感知风险，分别记作Ci1，Ci2，…，CiT；

（3）根据贝叶斯后验概率模型（式（14））计算得到量化感知风险Ci1，Ci2，…，CiT处于不同风险等级τ（包 括D，A，S）的 后 验 分 布 概 率 分 别 为｛PDi1，PAi1，PSi1｝，｛PDi2，PAi2，PSi2｝，…，｛PDiT，PAiT，PSiT｝；

（4）利用量化感知风险后验分布概率为权重对T段前瞻时间内的风险等级进行融合计算，得到预测区间内障碍车CARi对自车产生的融合感知风险HCARi：

式 中：PDit=P(τ=D│Cit)；PAit=P(τ=A│Cit)；PSit=P(τ=S│Cit)为自车处于不同风险等级的贝叶斯后验概率；τD、τA和τS分别取2、1 和0 以代表风险等级量化值。为方便后文实验验证，本文设定融合感知风险HCAR= 0.6 为临界风险阈值对驾驶场景进行风险评估。

3 实验分析

3.1 实车轨迹实验

筛选NGSIM 数据集US101-0805 样本中周边100 m 范围内存在至少两辆车的车辆轨迹片段进行风险评估实验，最终随机选取ID 为226 的车辆为自车CARv进行研究。该车在数据集中共出现482 帧（采样间隔0.1 s），选取与其相对距离小于100 m 的车作为周边障碍车辆，筛选得车辆ID 为217、218 的两辆车为对其行驶产生影响的周边车辆。该轨迹片段驾驶场景如图8（a）所示，自车CARv一直跟驰在前车CAR217后方沿高速公路内车道行驶，旁车CAR218初始行驶在自车相邻车道上，后发生换道加速插入自车CARv和前车CAR217之间。各车行驶轨迹如图8（b）所示。

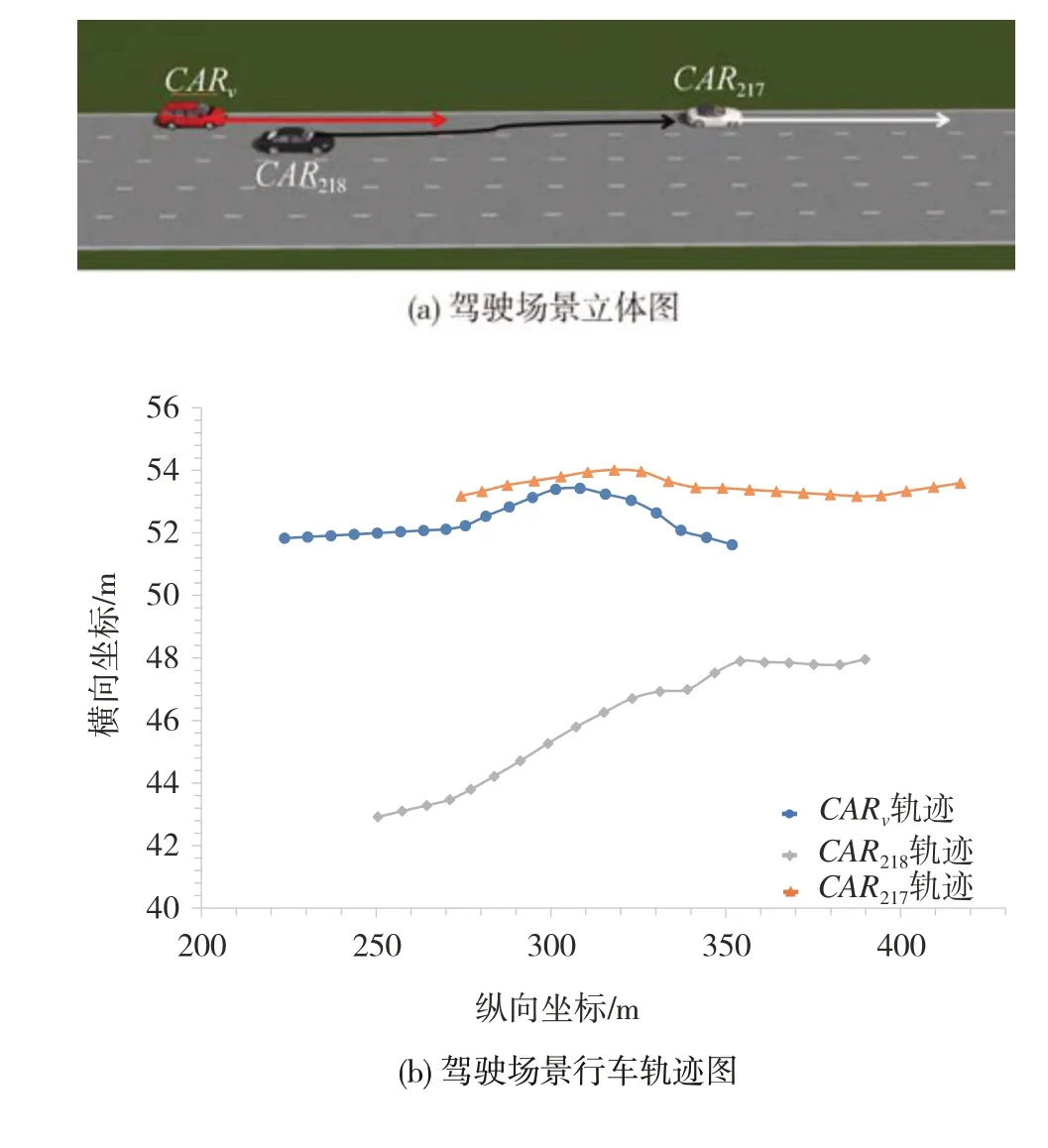
图8 实车轨迹实验驾驶场景示意图

采用环境注意力网络EA-Net 轨迹预测模型［14］对自车和周边车辆轨迹进行实时预测，按1.1 节所述方法构建自车的驾驶风险域DRF，按1.2 节所述方法得到事件成本在预测时间内的空间分布。轨迹预测模型输入为预测时刻过去1.5 s （共15 帧）作的自车与周边车辆的历史轨迹数据，输出为未来2.5 s（共25 帧）的预测轨迹数据。在所选轨迹片段中，以旁车CAR218作为障碍车为例，以旁车CAR218的换道时刻frame=1299 帧作为预测时刻，将自车CARv、前车CAR217和旁车CAR218第1 285至1 299帧共计15帧的历史轨迹数据输入EA-Net模型进行轨迹预测，得到各车第1 300 至1 324 帧共计25 帧的预测区间轨迹数据。根据图5 所示方法，将预测区间按时间窗时长为0.2 s、移动步长为0.1 s 划分为25 段前瞻时间（tla1=0.2 s），按式（9）计算得障碍车CAR218对自车CARv产生的量化感知风险时间序列如图9（a）所示。进一步，选取frame为1 265 至1 310 帧为实验区间（包括旁车CAR218的整个换道过程），以该区间内每一帧为预测时刻，按2.2 节步骤计算各时刻基于风险等级概率的融合感知风险HCAR变化趋势，如图9（b）所示。同理可对前车CAR217为障碍车时各个时刻自车的量化感知风险和融合感知风险进行计算。

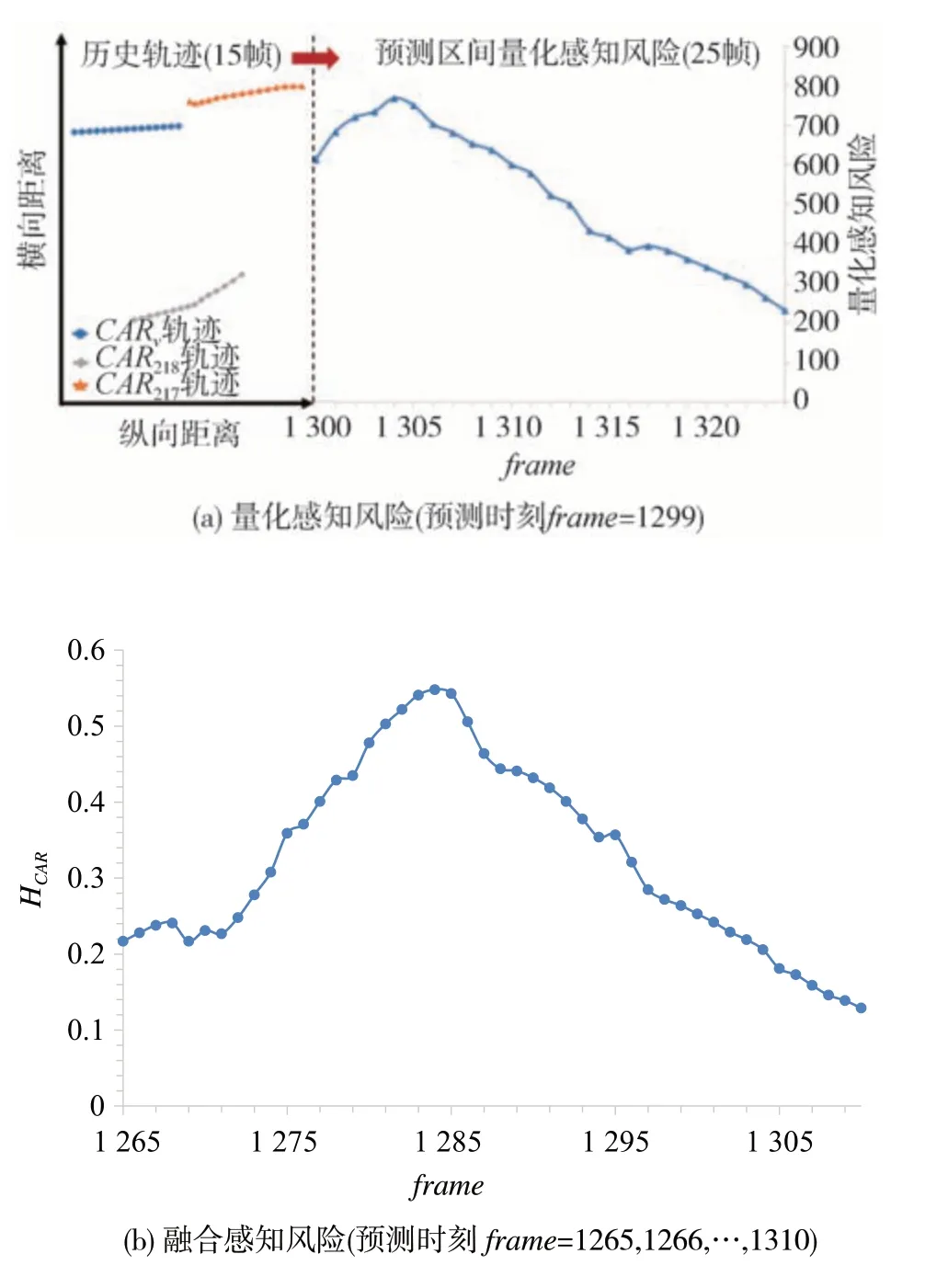
图9 障碍车CAR218对自车形成的风险预测

采用以碰撞时间TTC来测试本文基于预测轨迹量化感知风险的风险评估方法的有效性。为了避免两车相对速度很小导致TTC变为无穷大的情况，本文使用TTC的倒数ITTC（单位：s-1）进行评估，且在计算ITTC时，若前车车速大于后车车速则将ITTC记为负值。即ITTC为负值时代表没有驾驶风险，ITTC正值的增加表示驾驶风险的上升。选取TTC=2.4 s，即ITTC=0.4 s-1作为风险预警阈值［4］，即当ITTC≥0.4 s-1时，行驶车辆被视为危险状态。当旁车CAR218为障碍车时，实验区间（预测时刻frame=1265，1266，…，1310）内自车融合感知风险HCAR及ITTC趋势对比如图10所示。

由图10 可以看出，虽然融合感知风险HCAR和ITTC均低于各自的风险预警阈值0.6 和0.4 s-1，两者所显示的驾驶风险变化趋势差异性较大，HCAR曲线呈现了明显的风险升高和降落变化，而ITTC曲线大部分时间均小于0 且尾部保持在0 附近振荡。在真实驾驶场景中，自车CARv在行驶过程中按原车道行驶，障碍车CAR218初始车速大于自车CARv，在行驶过程中先减速后加速换道插入自车前方，之后继续加速行驶，且车速大于自车；其中，障碍车CAR218先减速后加速的换道过程实际对自车行驶产生了影响，自车行驶状态为先加速后减速再加速，这种影响与HCAR曲线所显示的风险先增大后减小的趋势一致。因此，与ITTC相比，HCAR可以更准确地体现出车辆换道过程中行车风险的变化，对复杂场景驾驶风险的预测具有更好的适用性。

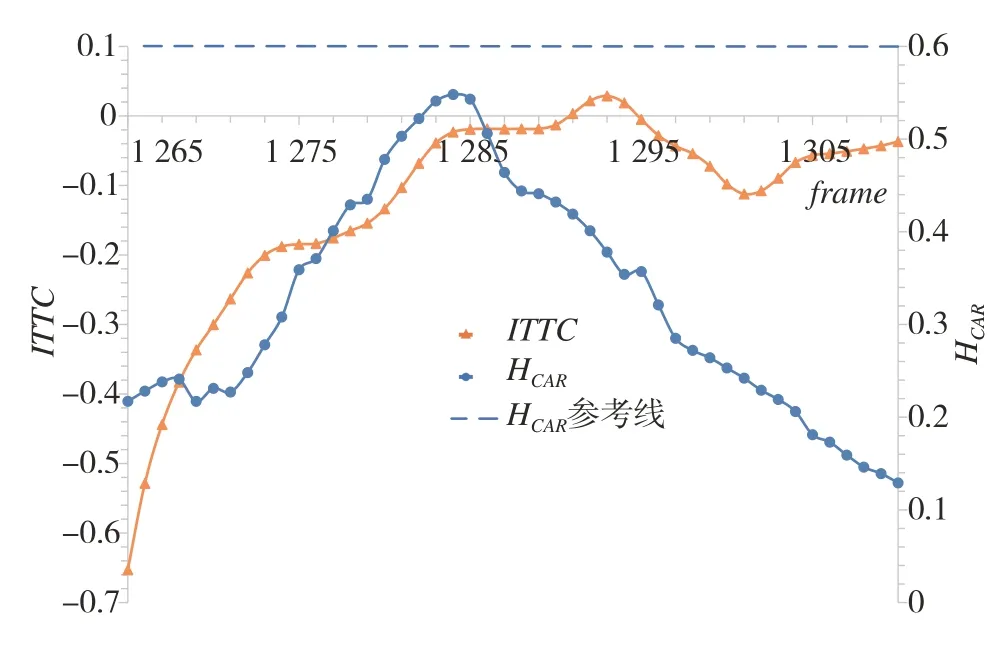
图10 融合感知风险HCAR和ITTC趋势曲线（障碍车CAR218）

3.2 仿真场景实验

利用Prescan 仿真软件构建车辆换道过程中的紧急事件场景来进一步验证本文基于预测轨迹量化感知风险的风险评估方法的有效性。仿真场景如图11 所示，场景中共有3 辆行驶车辆行驶在两车道高速公路上，其中黑车为自车CARv，红车为旁车CAR1，白车为旁车CAR2，车道宽度为3.5 m，在自车CARv左侧车道前方纵向距离15 和32 m 处分别是CAR1和CAR2。各车驾驶行为如下：（1）自车CARv初始速度为28 m/s，在并道场景中首先做加速度为2.5 m/s2的匀加速换道运动，从frame=52 帧开始换道插入CAR1和CAR2之间，在完成换道后做减速度为-7.2 m/s2的匀减速运动；（2）旁车CAR1初始速度为27 m/s，先做减速度为-2.0 m/s2的匀减速运动，后做加速度为6.4 m/s2的匀加速运动；（3）旁车CAR2初始速度为28 m/s，做加速度为1.0 m/s2的匀加速运动。自车CARv与旁车CAR1在frame=100 时（纵向距离151 m处）产生冲突交叉点，自车CARv与旁车CAR2无轨迹冲突。本节以自车CARv为研究对象，评估该场景中CARv由于突然并道行为造成的碰撞风险程度。

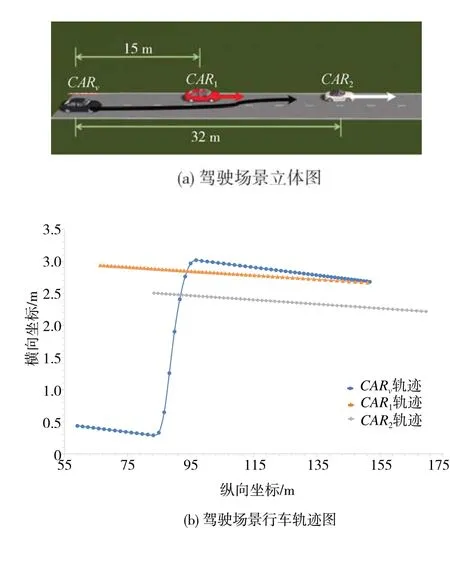
图11 Prescan仿真驾驶场景示意图

在上述仿真场景片段中，以自车CARv换道开始后frame=54 帧作为预测时刻，将自车CARv、旁车CAR1和CAR2第40 至54 帧共计15 帧的历史轨迹数据输入EA-Net 模型进行轨迹预测，得到各车第55至79 帧共计25 帧的预测区间轨迹数据。同实车轨迹实验将预测区间均匀划分为25 段前瞻时间（tla1=0.2 s），按式（9）计算得障碍车CAR1对自车CARv产生的量化感知风险时间序列如图12（a）所示。进一步，选取frame=62 至100 帧（碰撞发生前）为实验区间，以该区间内每一帧为预测时刻，按2.2节步骤计算各时刻基于风险等级概率的融合感知风险HCAR变化趋势，如图12（b）所示。同理可对旁车CAR2为障碍车时每时刻自车的量化感知风险和融合感知风险进行计算。

图12 障碍车CAR1对自车形成的风险预测

以碰撞时间的倒数ITTC为参照指标，当旁车CAR1为障碍车时，实验区间（预测时刻frame=62，63，…，100）内自车融合感知风险HCAR及ITTC趋势对比如图13所示。

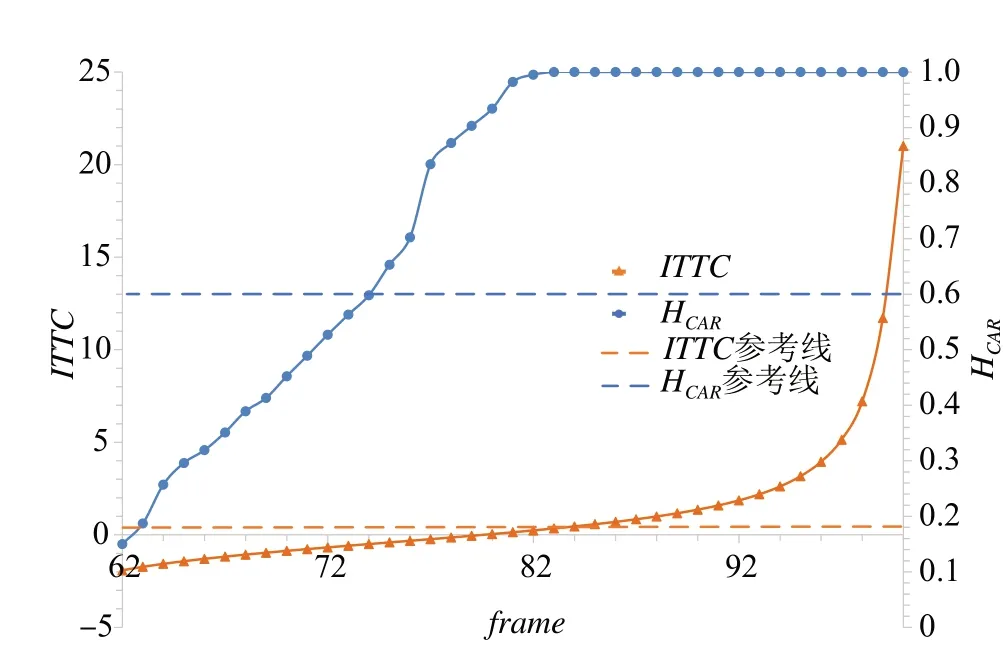
图13 融合感知风险HCAR和ITTC趋势曲线（障碍车CAR1）

根据并道仿真场景，自车初始位置位于旁车CAR1后方，且自车初始速度大于旁车CAR1，自车先进行匀加速运动超越旁车CAR1进行换道，同时旁车CAR1减速行驶让行，自车完成并道后做匀减速运动，旁车CAR1做匀加速运动，最终发生风险冲突。其中，由于自车在frame=53 帧时纵向上已超越旁车CAR1，此 处 以CAR1的 视 角 计 算frame=62 至100 帧CAR1与自车CARv之间的ITTC。由图13 可知，融合感知风险HCAR和ITTC呈现的驾驶风险趋势基本一致，但HCAR先于ITTC达到预设阈值。在frame=84时，ITTC超过了预设阈值，车辆行驶状态被评估为危险状态；而HCAR在frame=74 时就已经超过了0.6水平参考线，并在frame=83时达到峰值。可以看出，融合感知风险HCAR对风险的响应速度比ITTC更快，这主要是因为ITTC是基于车辆按照当前状态继续行驶的假设计算发生碰撞所需时间，而HCAR是在融合未来一段时间内自车与周边环境交互信息的量化感知风险的基础上获取的，可将驾驶员未来行车状态变化纳入量化风险的考虑范围，由此提高风险预测的及时性和准确性。

4 结论

本文针对周边多车复杂场景下的车辆碰撞风险问题提出了基于预测轨迹的行车风险评估方法，首先建立了沿预测轨迹两侧具有渐变高斯截面特征的驾驶风险域DRF以表征驾驶员行为的不确定性，然后考虑车辆与周围静态、动态障碍物处于特定状态的风险后果建立环境事件成本，得到适应复杂行车场景不确定性的量化感知风险，并基于贝叶斯理论融合预测区间内的量化感知风险时间序列，实现了对未来行车潜在碰撞风险的预测。实车轨迹和仿真实验结果表明，相比于经典TTC指标方法，基于融合未来一段时间内自车与周边环境交互信息的DRF的风险评估方法可以更快、更准确地辨识复杂交通场景的行车风险变化。未来将针对更多、更复杂的驾驶场景，通过仿真和实车试验进一步验证本方法的实用性。