考虑环境温度影响的超级电容SOC加权融合估计方法 *

2023-05-04张永志

汽车工程 2023年4期

王春，唐滔，张永志

（1.四川轻化工大学机械工程学院，自贡 643000；2.重庆大学机械与运载工程学院，重庆 400044）

前言

超级电容作为电动汽车混合储能系统的重要组成部分，其荷电状态（state of charge，SOC）估计是车载电源管理系统的核心功能之一［1-4］。SOC 估计精度将影响整车能量管理策略，因此提高超级电容SOC估计精度的研究显得十分必要［5］。

目前，SOC 估计方法分成4 类［6］：基于表征参数法、安时积分法、基于模型法和基于数据驱动法。其中基于模型法具有优秀的估计精度与鲁棒性，故该方法广泛应用在电动汽车的电源管理系统中［7］。其常用等效模型与状态估计算法结合的方式进行SOC估计。然而SOC估计精度和鲁棒性同时受状态估计算法影响［8］，因此诸多学者研究了不同的滤波算法应用于SOC 估计中。如扩展卡尔曼滤波（extended Kalman filter，EKF）算法［9］、自适应扩展卡尔曼滤波（adaptive extended Kalman filter，AEKF）算法［10］、无迹卡尔曼滤波（unscented Kalman filter，UKF）算法［11］、自适应无迹卡尔曼滤波算法［12］、容积卡尔曼滤波［13］、粒子滤波算法［14］、H∞滤波算法［15］、非线性观测器［16］和集员估计［17］等。

为解决上述估计方法对SOC估计精度提升困难的问题，许多学者提出了融合估计SOC 的方法。从事状态估计研究的熊瑞博士提出一种基于H∞滤波估计的多模型概率融合估计［18］SOC方法。采用H∞滤波与3 种等效电路模型结合分别估计出SOC，然后基于贝叶斯定理加权融合输出SOC的估计值。虽然该方法比基于H∞滤波的单个模型估计SOC 的准确性和鲁棒性均有提升，但是缺少考虑温度对SOC 估计精度的影响。之后，将上述方法应用到能量状态的估计［19］，并验证了不同温度下的估计精度均有提高。紧接着，熊瑞博士等［20］发现模型的残差均值和方差在不同的老化程度下存在某些关系，并依据这些关系融合模型。利用积分差分观察器进行SOC和SOH 联合估计，同样通过贝叶斯概率理论进行权重分配融合3 种模型估计的状态值。此外，为提高融合估计精度，王超团队［21］提出了多模型融合估计方法。该方法是基于每个模型端电压的估计误差采用贝叶斯概率理论融合3 种模型的SOC 估计值，同时改进了自适应无迹卡尔曼滤波，使得融合估计的噪声随时间更新。比较融合前，该方法具有更好的SOC 估计精度和鲁棒性。田野和宋凯［22］提出基于AEKF 算法的多模型融合估计SOC。条件概率分配SOC 融合的权重是以考虑电池温度特性和倍率特性的两种电池模型估计值与测量值残差为依据。该方法能够实现较高的SOC估计精度。文献［23］中提出一种基于荷电状态残差的两层融合模型，它是基于贝叶斯定理、残差归一化和SOC 碎片化分段融合，再基于均方根误差决策融合模型的两层融合方法。除了多模型融合，Fu 等［24］用贝叶斯概率融合两种容积卡尔曼滤波器估计的SOC 值。实验证明该方法常温环境中能够提高SOC 的估计精度。另外王榘等［25］提出了一种基于扩展卡尔曼滤波算法的多阶段模型融合的SOC 与SOH 协同估计方法，该方法有较高的估计精度与鲁棒性，并且考虑了温度的影响。一方面融合多模型的SOC 估计值能提高估计精度，另一方面直接融合模型也能间接地提高SOC估计精度。

综上所述，融合估计方法多是模型融合估计方法，并且少有考虑温度对状态估计的影响。针对这些问题，本文中提出了考虑温度影响的超级电容SOC 加权融合估计方法。首先考虑了温度的影响，把温度参数作为变量，建立了超级电容的变温模型；然后，基于Thevenin 模型采用3 种滤波算法融合估计SOC；最后，通过模拟对比分析了3 种加权融合方式融合估计SOC的误差。

1 超级电容建模与参数辨识

1.1 超级电容建模

经过近几年的发展，Thevenin 模型被广泛地应用于基于模型的SOC 估计中，并且具有较高的模型精度和结构简单的特点。因此本文中采用该模型作为超级电容的等效电路模型［26］。图1 展示了Thevenin 模型电路结构，Uocv为理想电压源的开路电压，R0是描述超级电容的欧姆内阻，Rd为极化电阻，Cd为极化电容，iL和Ut分别是工作电路的端电流和端电压。

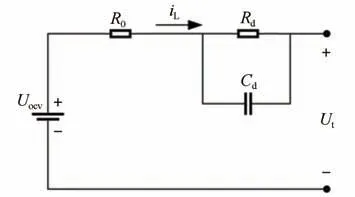
图1 Thevenin模型

Thevenin模型的状态方程表达式：

式中：τ=Rd×Cd；k表示时刻；Δt是此刻与前一时刻的时间间隔。

1.2 超级电容实验

为了构建变温模型，需要获取不同温度下的超级电容特性实验数据，搭建的实验测试平台主要是由ARBIN BT-5HC-5 V-100 A 测试系统、温度箱和上位机组成。测试系统能对超级电容进行充放电，并能实时监测超级电容的电压与电流。测试系统电压和电流测量范围分别是0～5 V 和-100～100 A。温度箱能确保超级电容周围环境温度恒定，其温度调节范围是-40～100 ℃。上位机主要完成对测试系统的控制、收集和存储实验数据。实验采用的是Maxwell 公司生产的1 500 F 超级电容器，主要技术参数在表1中展示。

表1 超级电容技术参数

实验包括HPPC 测试和UDDS工况测试，并分别设置在-10、10、25和40 ℃ 4个恒温环境下进行测试。整理不同温度下HPPC 测试和UDDS 工况测试的实验数据，为后续研究做好准备。图2展示了HPPC测试和UDDS 测试实验的电压与电流曲线。由图可见，随着温度升高超级电容静置后的初始电压越低。

图2 HPPC和UDDS测试电流与电压数据

1.3 温度-SOC-OCV曲面拟合

超级电容的荷电状态（SOC）用剩余容量与最大可用容量之比表示，表达式如下：

式中：Qt为超级电容当前剩余容量；Qmax为超级电容的可用容量。为了减少Qmax影响温度-SOC-OCV 曲面拟合精度，从HPPC 实验数据中获取。超级电容SOC随时间变化情况的计算公式如下：

式中：SOC0为SOC的初始值；η为充放电效率；iL为电流。若要通过计算机运算，则需要对上式进行离散化。通过k-1时刻获得k时刻SOC的离散关系式：

理想条件下超级电容的SOC 与开路电压（open circuit voltage，OCV）近似成线性关系，但是受多方面因素影响，曲线精度也将直接影响参数辨识和SOC估计精度。考虑到温度对曲线的影响，建立温度与SOC-OCV 三维响应曲面。处理4 个不同温度环境下HPPC 测试的实验数据，得到温度-SOC-OCV 曲面方程。建立端电压OCV 关于温度和SOC 的二元多项式方程：

式中ai（T）是关于温度的多项式系数。考虑温度的多项式系数如表2 所示。函数在三维空间的响应曲面由图3展示。

表2 多项式系数

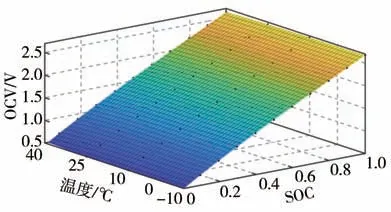
图3 温度-SOC-OCV三维响应曲面

1.4 参数辨识与验证

准确的模型参数对提高SOC 估计精度十分重要。为得到等效电路模型参数R0、Rd和Cd的值，采用粒子群优化算法（PSO）辨识。该算法在1995 年被Eberhart 博士和Kennedy 博士提出，依据鸟群捕食行为和捕食规律建立的算法。鸟群的个体与每个粒子一一对应，每个粒子通过自己对目标距离的判断和群体共享的信息去改变自己当前位置与移动速度。随时间推移，鸟群将聚集在目标附近，鸟群位置被视为优化目标的最优解。参数辨识的目标函数如下：

式中：fmin（R0，Rd，Cd，T）是需要优化的目标；Ut，k为k时刻的测量端电压；Ut，k（R0，Rd，Cd，T）表示端电压的估计值，R0、Rd、Cd是要辨识的参数，T是环境温度。通过PSO 辨识得到图4 中各温度下模型参数辨识结果。

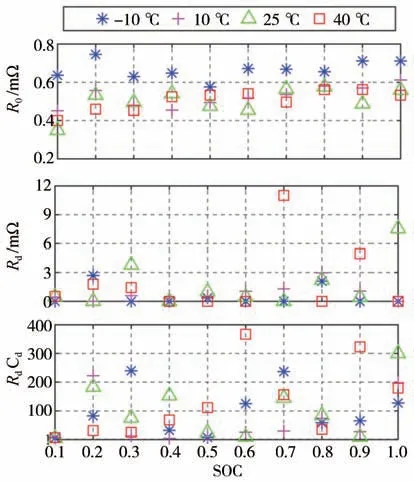
图4 模型参数辨识结果

为更好反映辨识参数的准确性，使用UDDS 工况测试验证Thevenin 模型精度。验证时，为得到不同状态的模型参数值，采用最近邻点插值法建立温度-SOC-参数响应关系。图5 展示了UDDS 工况验证下的模型端电压误差。在此工况下，温度从-10到40 ℃的端电压误差最大绝对值分别是8.58、8.91、11.77 和8.91 mV。其最大值出现在环境温度为25 ℃的第6 838 s，大多时刻的误差保持在8 mV以内。它们的平均绝对值误差分别为1.8、1.9、1.7和1.6 mV，也表明其误差都保持在很低的水平。通过验证分析，基于粒子群算法辨识的参数和Thevenin 模型可以非常精准的模拟超级电容充放电机理。在-10 到40 ℃范围内非常高的精度，符合应用要求。

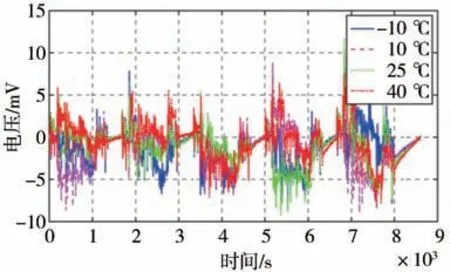
图5 UDDS工况验证下的端电压误差图

2 状态估计算法

状态估计算法是实现SOC在线估计的重要组成部分，其中卡尔曼滤波算法被广泛的应用在各个领域中。考虑到融合估计的机理，选择相似的3 种卡尔曼滤波算法，分别是扩展卡尔曼滤波、无迹卡尔曼滤波和自适应扩展卡尔曼滤波。

2.1 扩展卡尔曼滤波

EKF被Stanley Schmidt最先提出，为解决非线性系统的实时估计问题。EKF 常用f（xk-1，uk-1）表示状态方程函数，h（xk-1，uk-1）表示系统观测方程函数，表达式如下：

式中：x是n维系统状态向量；u是λ维的系统输入向量；y表示m维的系统观测值的输出向量；ω为系统的白噪声；v是系统的测量白噪声。

在实际应用中，计算机只能处理离散的数据。为解决不能处理连续状态系统的问题，连续的系统状态方程通过泰勒展开式进行离散化处理。离散处理后的状态方程如下：

2.2 自适应扩展卡尔曼滤波

为解决EKF 滤波算法噪声协方差值固定不变导致估计稳定性较差的现象，引入噪声协方差自动匹配的方法。噪声协方差会随滤波算法估计结果的变化进行更新，实现噪声协方差的自适应过程，以此提高EKF 滤波算法的估计稳定性和精度。自适应扩展卡尔曼滤波算法在扩展卡尔曼滤波基础上增加了自适应过程。

式中M为自适应窗口长度。

2.3 无迹卡尔曼滤波

EKF 和AEKF 对于强非线性系统的估计精度降低。S.Julier 等提出了一种适合强非线性系统的无迹卡尔曼滤波，其用无迹变换替代扩展卡尔曼滤波的滤波状态与观测方程。通过无迹变换得到估计值附近的点，这样的点被称为采样点。然后求得这些采样点的均值和协方差的特征，并与原统计特征相匹配，再进行采样点的映射。该方法是基于概率统计得到的近似估计。其中UT 变换在无迹卡尔曼滤波当中是十分重要的，下面是UT变换的过程。

通过计算得出2n+1个采样点：

然后计算每个采样点的权值：

式中：ωm为计算均值的权值；ωc为计算协方差的权值；上标i为采样点序号；n为状态维度；λ为缩放比例，用来降低总的预测误差，λ=α2(n+κ) -n，κ为待定系数，一般取κ=0 或3-n；α为控制采样点分布状态系数，取值区间为［0，1］；β为非负权系数（β≥0），取0或2，当β=2时，采样点为高斯分布。

无迹卡尔曼滤波估计SOC的步骤如下。

最后进行时间尺度上的更新，k时刻的状态输出和协方差矩阵作为k+1 时刻的输入，进行下一时刻的估计运算。

3 融合估计方法

基于等效电路模型的SOC估计方法在估计精度和鲁棒性上都有很好的表现，然而通过滤波算法提高SOC 估计的精度却很困难，因此SOC 融合估计方法被提出来。目前，融合结构分成3类［18-19］：集中式、分布式和混合式。其中混合式融合结构虽然比其他结构有更好的精度表现，但是其计算量大，结构复杂，不利于应用到电动汽车的状态实时估计。不同的融合结构具有不同特点，普遍认为集中式融合优于分布式融合的性能，但是有研究表明分布式融合也存在优势。熊瑞博士等［18］用分布式结构进行多模型融合估计SOC，并证明该方法的可行性。在此基础上，本文中采用分布式结构进行SOC 融合估计。3种滤波算法分别估计超级电容的SOC，然后经过融合中心加权融合SOC估计值。融合中心采用模糊熵理论分配权值，并选用另外两种分配权值的方法作对比。另外两种方法分别是基于残差归一化的权值分配方法和基于自适应加权平均的权值分配方法。图6为本文提出的SOC融合估计框架。

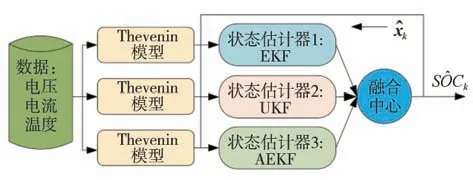
图6 融合估计的框架

3.1 基于模糊熵加权融合估计SOC

基于模糊熵加权融合（fuzzy entropy weighted fusion，FEWF）估计SOC 的融合中心是依据1968 年Zadeh L A 提出的模糊熵理论加权。时至今日，模糊熵的理论在许多领域得到了广泛的应用。模糊熵的计算公式［27］如下：

式中：SÔC(k)是第k时刻输出的SOC 估计值；ωi（k）是第k时刻不同滤波器对应下的权值；SÔCi(k)是第k时刻第i个滤波器估计的SOC 值，滤波器的个数为n。

3.2 基于残差归一化加权融合估计SOC

归一化是将有量纲的数据转变成无量纲数据的一种手段，并把数据映射到0～1 区间内。基于残差归一化加权融合（residual normalized weighted fusion，RNWF）是将SOC 估计值所对应的端电压和实际的端电压作差，得到此刻各个滤波器估计的残差值，在不考虑其他因素的影响下，通过式（41）得到k时刻SOC估计值。式（42）是权值限定关系：

3.3 基于自适应加权融合估计SOC

自适应加权融合［28］（adaptive weighted fusion，AWF）常用于多传感器信号处理。通过找出各自最优的加权因子，使得总的均方误差最小。其权值满足式（43）的要求，通过式（41）计算k时刻SOC估计值。

最小总均方误差：

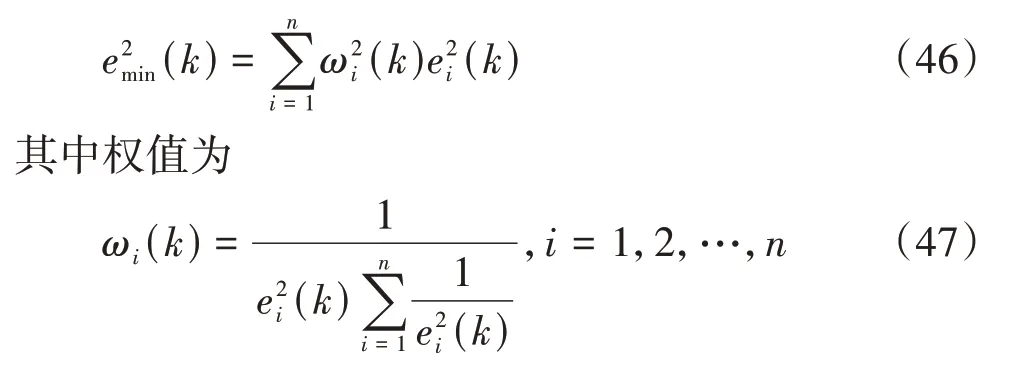
式中：ωi(k)为第k时刻的第i个滤波器的最优权值；ei（k）为第k时刻第i个滤波器估计的端电压与实际端电压的残差值。

4 实验与估计结果分析

为验证融合估计算法能够提高SOC 估计精度，实验采用UDDS 工况测试数据模拟超级电容SOC 估计。该过程中模型参数采用最近邻点插值，超级电容容量根据温度通过线性插值法获取。-10、10、25和40 ℃ 4个温度下的仿真测试结果如图7所示。图中展示了基于模糊熵加权融合、基于自适应加权平均融合和基于残差归一化加权融合估计SOC的实时估计值与真实SOC 的误差值，同时加入3 种卡尔曼滤波估计结果对比分析。为更加直观对比各个方法的SOC 估计精度，采用最大绝对误差（max absolute error，MAX）、平均绝对误差（mean absolute error，MAE）和均方根误差（root mean squared error，RMSE）为评判指标。各个误差分别按照式（48）～式（50）计算，并通过表3展示了6种估计结果的误差。

式中：i为样本序列，共有N个；SÔCi和SOCreal，i分别为估计值与实际值。

温度在-10、10、25 和40 ℃下，实验得到不同估计方法的SOC 估计结果和估计误差，如图7 所示。通过图7中（a）、（c）、（e）和（g）可知，各方法均能实时准确地估计SOC的值。为更加准确地分析各个方法估计SOC的精度，观察图7中（b）、（d）、（f）和（h）的误差变化可以发现，UKF 算法估计精度更容易受到SOC 影响，EKF 和AEKF 算法估计误差变化趋势相近。对比EKF 和AEKF 算法估计SOC 误差变化，UKF 算法估计误差曲线局部向纵坐标负方向移动，并随温度的上升变化越显著。为了定量分析图7 的SOC 估计结果，表3 给出了各个估计方法在上述给定的温度下在UDDS 工况中的SOC 估计值与真实值的MAX、MAE 和RMSE。UKF 算法估计最大绝对误差在不同温度均大于EKF 和AEKF 算法。-10 和10 ℃时，AEKF 比EKF 和UKF 算法估计最大绝对误差更小；25和40 ℃下EKF算法估计最大绝对误差更小。以MAE 和RMSE 做比较时，EKF、UKF 和AEKF算法估计精度在不同温度下的表现不同。由此可见各卡尔曼滤波算法估计SOC各有优势。

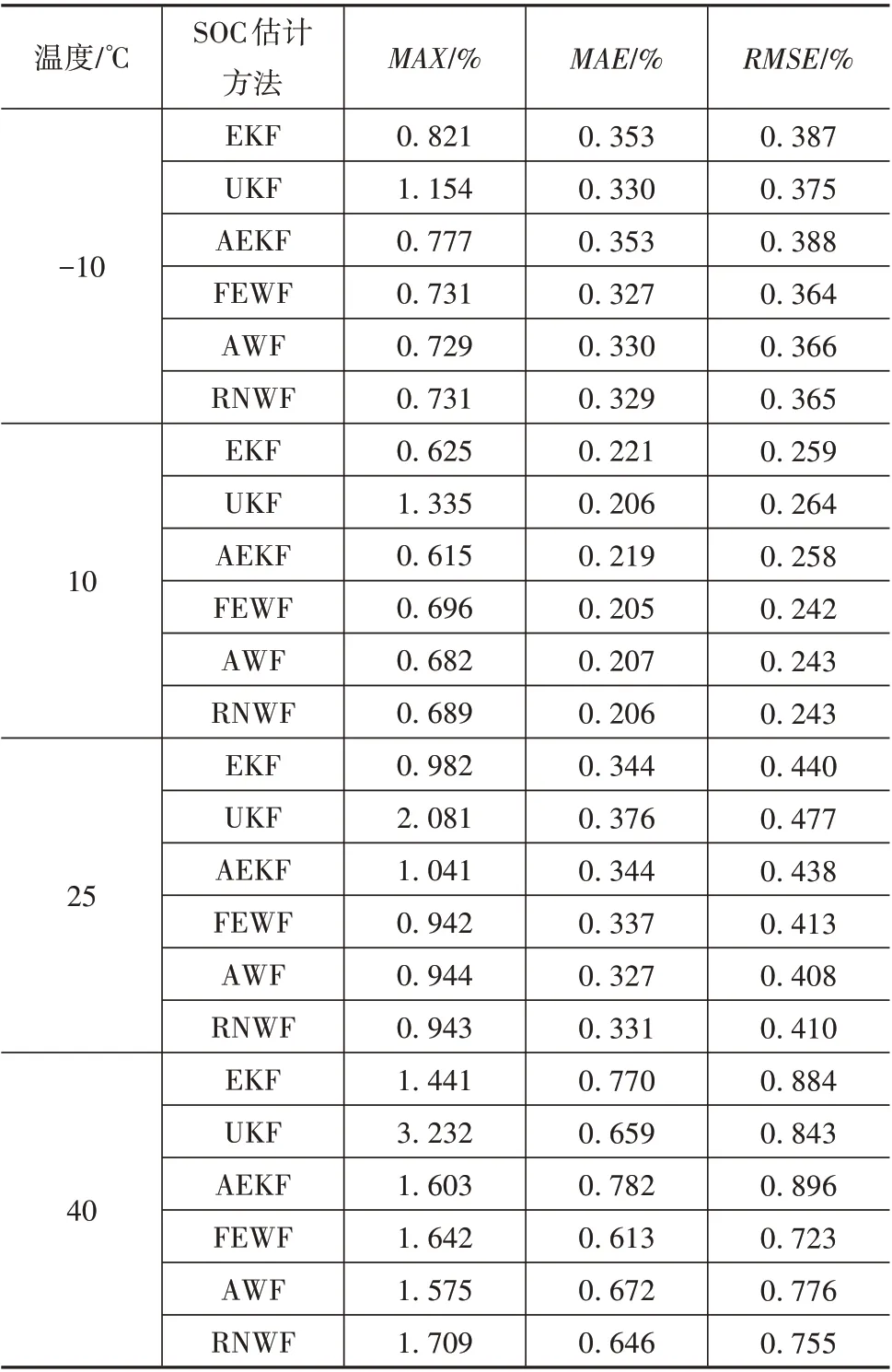
表3 SOC误差分析

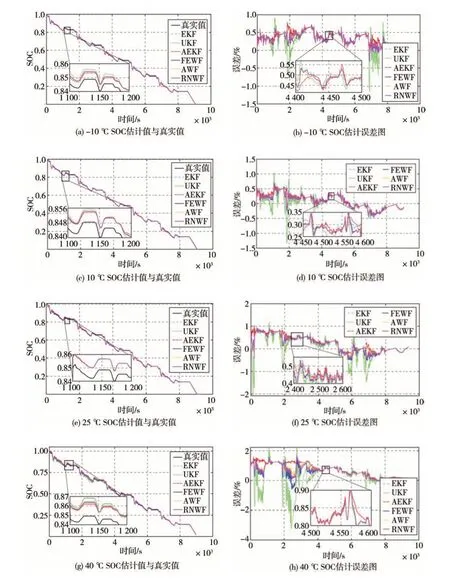
图7 UDDS工况不同温度下超级电容SOC估计值与误差图

观察图7，3 种滤波算法加权融合估计SOC 的误差曲线向0趋近，在4个不同温度下SOC估计精度均有不小的提升。为更加直观地体现各个融合方法估计SOC 精度的提升，选择3 种单一滤波估计SOC 中对应评判指标下误差最小的作为对比。通过表3 分析：以MAE为依据，基于模糊熵加权融合估计SOC的精度在-10、10、25 和40 ℃分别提升了0.9%、0.5%、2.0%和6.9%；以RMSE为评判指标，误差降低了2.9%、6.2%、5.7%和14.2%；基于模糊熵加权融合估计SOC 的MAX仅在-10 和25 ℃时最小。基于残差归一化加权与自适应加权融合估计以MAE为评判标准，基于自适应加权融合估计SOC 的精度仅在25 ℃时提升了4.9%。基于残差归一化加权融合估计SOC 在温度为-10、25 和40 ℃时精度得到了提升，与对应温度下精度最高的单一滤波估计对比至少提升了0.3%、3.7%和1.9%。在用RMSE作为评价依据时，基于自适应加权融合估计方法在4 个环境温度下的SOC估计精度对比相应温度下精度最高的单一滤波估计精度分别提升了2.4%、5.8%、6.8%和7.9%，基于残差归一化加权融合估计SOC的均方根误差降低了2.6%、5.8%、6.3%和10.4%。用MAX比较时，对比相应温度下精度最高的单一滤波估计只有在25 ℃时有提升，却没有基于模糊熵加权融合估计提升明显。从上述比对数据比较得出，作为对比的两种融合方法在25 ℃温度下SOC 估计提升效果均比模糊熵加权融合方法更好，然而其他环境温度下提升力度不如基于模糊熵加权融合估计SOC 方法，并且基于自适应加权融合估计方法在以MAE做评价时出现估计精度下降的现象。对比上述两种融合估计方法，基于模糊熵加权融合估计在提升SOC估计精度上有显著的效果。