基于相空间三维动态稳定域的重型车辆稳定性控制策略研究 *
2023-05-04康宇航李韶华杨泽坤
康宇航,李韶华,杨泽坤,2
(1.石家庄铁道大学,省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043;2.湖南大学机械与运载工程学院,长沙 410082)
前言
与乘用车相比,重型商用车整车转动惯量较大,对转向输入的响应缓慢[1],其动力学特性更加复杂[2]。因此,在复杂行驶环境下存在较大交通安全隐患,其事故总量占交通事故总量的份额逐年上升,截至2016 年已占47.08%,造成直接经济损失近2.5亿元;2020 年,我国交通事故发生总量为24.47 万起,直接财产损失金额为131 360.6万元。发展兼顾循迹精度[3]、动力学稳定性[4]等多目标重型商用车辅助驾驶技术是解决行驶安全问题的重要方向。
车辆动态稳定性对车辆运动学控制有着重要影响[5],钟龙飞等[6]基于β-β̇相平面估计稳定区域,设计了汽车横向控制策略,但质心侧偏角不能准确实时测量,且并未考虑动态稳定性。丛森森等[7]使用汽车横向速度和横摆角速度建立横向动态稳定区域,但并未考虑车辆的侧倾稳定性。
目前,基于稳定域的车辆稳定性控制方法已得到广泛应用,但其在稳定性控制方面仍有一些不足。虽然稳定域边界被准确清晰地推演[8],但在实际应用过程中缺乏直观简洁的描述。由于稳定域在不同车速和转向角度时可显著移动[9-10],在面对不同转向角度和车速时因缺乏直观表达而难以实际应用。另外,基于汽车行驶稳定性指标设计调度参数[11]的控制算法在轮胎力饱和的情况下可能并不会被有效执行,从而影响控制效果。
本文中针对重型商用车的极限工况设计了基于可拓H∞的AFS/DYC分级控制策略,提出了以横摆角速度-质心侧偏角-垂向载荷转移系数相平面为基准的稳定性判断依据作为AFS/DYC的分级条件。基于输出反馈鲁棒H∞控制方法和商用车4自由度动力学模型设计了H∞控制器,通过车轮的附着极限来设计可拓控制方法,由附着系数确定控制器增益。最后采用TruckSim/Simulink 联合仿真和硬件在环实验验证了双移线工况和紧急避障工况下控制算法的有效性。
1 车辆动力学模型
建立包括纵向、横向、横摆、侧倾4 个自由度的车辆动力学模型,如图1所示。
图1中,a、b1、b2分别为质心到前轴、中间轴和后轴的距离,B为轮距,β为车辆的质心侧偏角,ψ̇为横摆角速度,CoG为车辆的质心位置。
车辆的纵向、横向、横摆、侧倾方程如下:
式中:m、ms分别为汽车的总质量和簧上质量;vx、vy分别为车辆的纵向速度和横向速度;ψ、ϕ分别为车辆的横摆角、侧倾角;hs为簧上质量质心至侧倾轴线距离;Ixx、Izz分别为簧上质量绕x、z轴的转动惯量;Ixz为簧上质量绕x、z轴的惯性积;ΣFx、ΣFy分别为汽车在纵向和横向所受的合外力;ΣMx、ΣMz分别为簧上质量受到绕x轴的侧倾力矩、绕z轴的横摆力矩;B为车轮的左右轮距。
结合式(1),可将车辆动力学方程表示为

将前轮转角δ和车辆所受干扰横向力Fˉy定义为干扰输入ω,将附加前轮转角Δδ和附加横摆力矩T定义为系统的控制输入u:

式中:As为摩擦衰减系数;v为汽车速度;C为轮胎刚度;sx为纵向滑移率;α为轮胎侧倾角。
前、中、后轮胎侧偏角αf、αm、αr如式(6)所示:
2 车辆稳定性指标设计
为了确定车辆稳定性边界,明确车辆在相空间中的动力学状态具有重要意义。由于质心侧偏角在实际测量中往往存在较大的误差,所以β-β̇稳定性边界的方法精确性相对较低。本文采用的质心侧偏角-横摆角速度-垂向载荷转移系数(β-ψ̇ -LTR)相图能够在不同工况下有效表示车辆横向、横摆、侧倾方向上的状态,进而确定相应的稳定边界[12]。
由式(1)的横摆动力学方程可以得出汽车的最大稳态横摆角速度ψ̇max,ss:

式中:βf,max、βf,min为前轮所决定的质心侧偏角最大、最小值;αsl,f为前轮的最大侧偏角。
假设汽车后轮转角可忽略不计,故由汽车后轮的侧向动力学方程可以得到稳态质心侧偏角临界值:

式中:ll、lr分别为左右轮距离质心的横向距离;Fzl、Fzr分别为汽车左右侧车轮垂向力的合力;Fz为车轮垂向载荷。

将式(13)代入式(8)和式(9)可得到β与LTR的4 个函数,式(8)为具有负斜率的两条直线,式(9)为具有正斜率的两条直线。LTR的范围取为(-0.79,0.74),可根据式(8)和式(9)得到β的取值范围为(-11.6,11.3),每个LTR 值对应式(8)和式(9)得到的4 个质心侧偏角。以上β-LTR关系如图2(a)所示。
取车速25 km/h、路面附着系数0.8,前轮转角设为0,由式(7)可计算得到最大稳态横摆角速度为(-18,18)(°)/s。进而由式(8)和式(9)可以得到质心侧偏角的最大最小值为(-11.7,11.5)(°)。最终表现为质心侧偏角-横摆角速度(ψ̇ -β)相图中的稳定边界,如图2(b)所示。
结合式(7)~式(9)及式(13),可得到β-ψ̇ -LTR三维相空间中的边界,如图2(c)所示。图中蓝线为各边中点的连线。
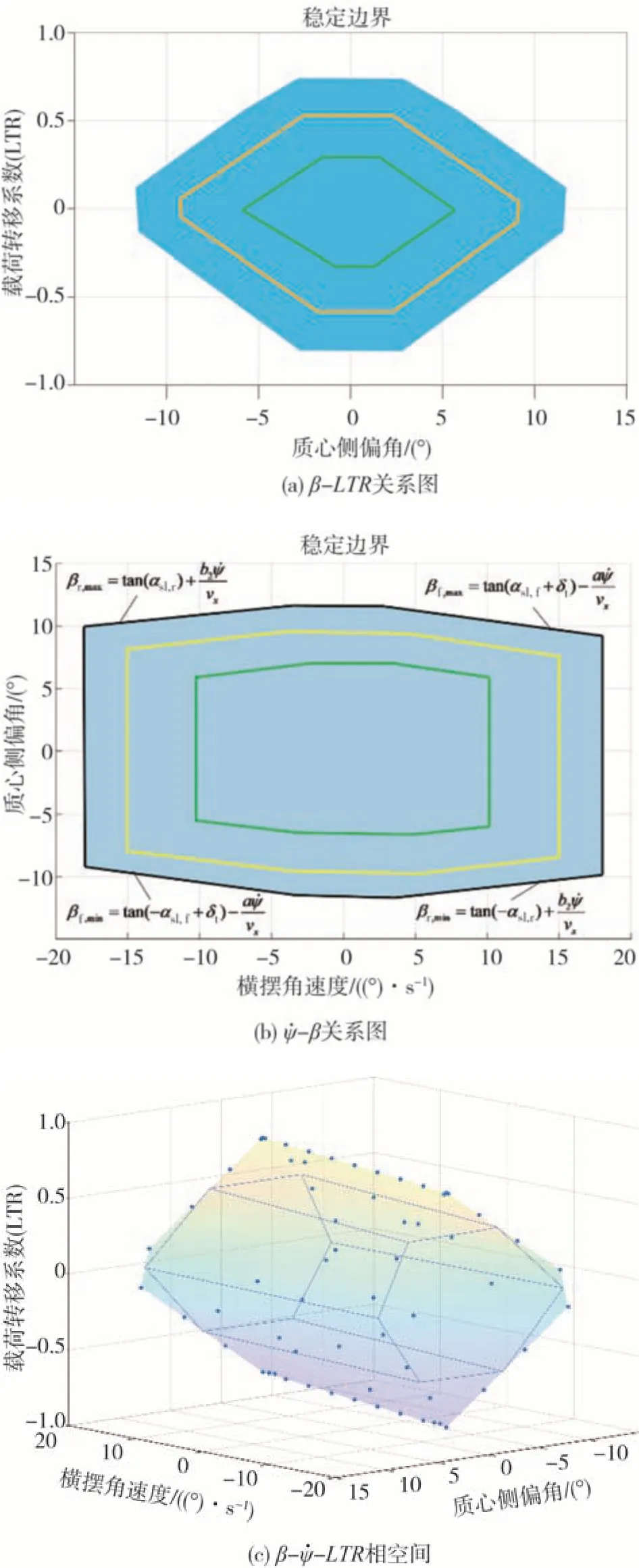
图2 β - ψ̇ - LTR稳定边界
为实现车辆的AFS/DYC 分级控制,划分稳定边界为3 个区域,分别为稳定区域(边界的0.6 倍)、预警区域(边界的0.6~0.85 倍)、危险区域(超出临界区域的部分)。分别显示为图2(a)和图2(b)中绿线以内的部分、绿线黄线之间的部分以及黄线以外的部分。
3 鲁棒H∞控制器设计
3.1 H∞控制方法设计
基于H∞的AFS/DYC 车辆稳定性控制逻辑如图3 所示。获取车辆的横摆角速度、车速、前轮转角等参数后,估计质心侧偏角和轮胎力,通过相空间动态稳定域进行稳定性判断,在稳定区域不控制、危险区域AFS控制、临界区域AFS/DYC控制。
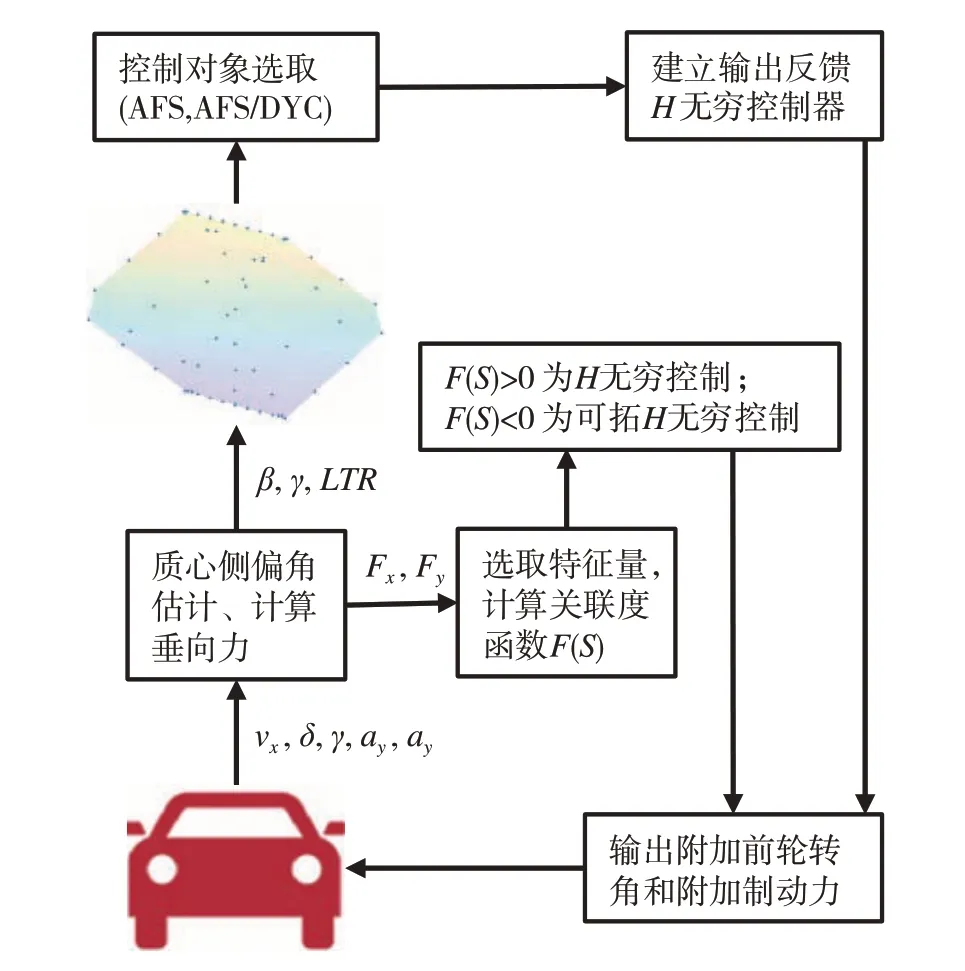
图3 控制流程图
寻找如式(3)第1式形式的输出反馈H∞控制器:
式中:x̂为nk阶控制器的状态;Ak、Bk、Ck、Dk为待定的控制器参数矩阵。将上述的控制器应用至系统,得到如下的闭环系统:

式 (14)控制器使得式(15)闭环系统渐进稳定且从ω到z的传递函数的H∞范数小于γ的充分必要条件是存在一个对称正定阵Xc使得

闭环系统中各个系数矩阵可表示为如下控制其参数矩阵K的仿射函数:
将式(17)代入式(16)中,得到如下线性矩阵不等式(Linear matrix inequality,LMI):

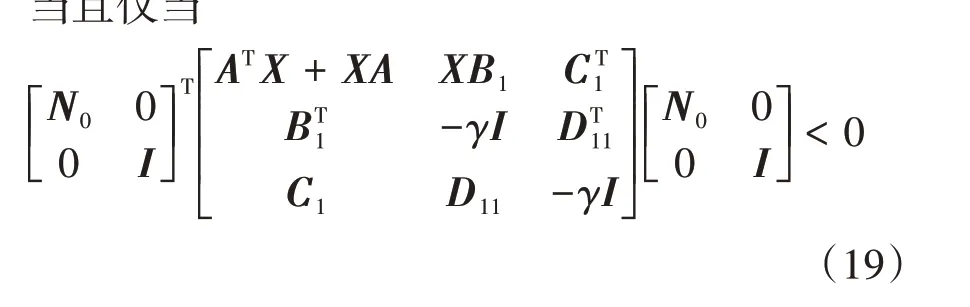

将得到的矩阵Xc代入式(16)不等式,得到只包含K的一个LMI,因此可以用标准的LMI 求解方法解出K。由投影定理可知,矩阵Xc的存在性保证了上式对矩阵K的可行性。
3.2 可拓控制器设计
为了改善AFS/DYC 控制系统的性能,基于可拓控制理论对H∞控制器的输入信号进行动态调整。可拓控制器的设计主要包括以下步骤:特征量选取、可拓集合划分、关联度函数计算和控制策略选择。
在本文设计的控制策略中,可拓控制的作用是根据车辆状态对控制量附加前轮转角和附加横摆力矩进行进一步完善,具体指的是若附着力不足,可拓控制策略会让车辆更加倾向于直线行驶,减小车辆所受横向力,从而达到改善车辆稳定性的目的,所以添加可拓控制不会影响到系统的稳定性问题。
可拓集合划分如图4 所示。Fxb、Fyb分别为地面所能提供的最大纵向力和最大横向力。
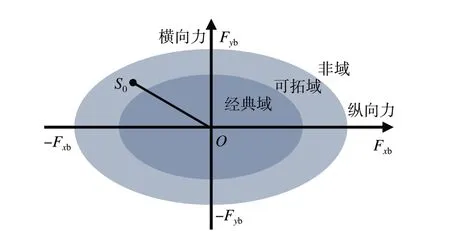
图4 可拓集合划分
F(S) >0 时为经典域,此时地面可提供充足摩擦力;-1 <F(S) <0 时为可拓域,此时地面提供的摩擦力接近阈值;F(S) <-1 时为非域,此时汽车所需的力大于轮胎的附着极限。

ka指的是经典域的范围,根据车辆的种类、常用驾驶环境甚至驾驶员驾驶习惯来确定。本文通过仿真实验发现,高于0.6 时稳定性控制效果较差,低于0.6 时稳定性控制介入过早,对于驾驶员意图影响过大,因此将此系数取为0.6。
根据式(22)计算的关联度函数值能够在对应区域决策出车辆在不同工况下的控制策略以及控制器的输出值μ。可拓H∞控制器的控制输出为
式中Fc为系数矩阵。
4 仿真实验
为了验证所设计的AFS/DYC 控制器的有效性,采用TruckSim/Simulink 联合仿真,对比分析可拓H∞控制和H∞控制对汽车稳定性的影响。受控车辆模型参数如表1所示。
在输入预定轨迹的情况下选取双移线工况、减速避障工况进行仿真。其中双移线工况车速为80 km/h,路面附着系数为0.3。减速避障工况由GB/T38186—2019 所规定的AEBS 法规制订,初始车速80 km/h,障碍车车速30 km/h,初始距离210 m,路面附着系数为0.8。
采用两种稳定性判断方法:一种为第2 节中β-ψ̇ -LTR三维相空间判断方法;另一种为传统的β-ψ̇二维相平面判断方法,再与无控制的情况进行对比分析。
4.1 附着系数0.3双移线工况
车速80 km/h 路面附着系数为0.3 的双移线工况,行车轨迹、横摆角速度、质心侧偏角、纵向车速、前轮转角数据如图5 所示。无控制、使用二维相平面、使用三维相空间判断稳定性时3 种情况下的横摆角速度、质心侧偏角变化幅值见表2。
由图5 和表2 可知:车辆在无控制的情况下7 s后处于横向失稳状态,不能按照预定轨迹行驶;但在所设计的可拓H∞控制器作用下,车辆完整地完成了双移线工况,且在β-ψ̇ -LTR相空间稳定性判断作用下,车辆摆动明显小于β-ψ̇相平面稳定性判断的情况。
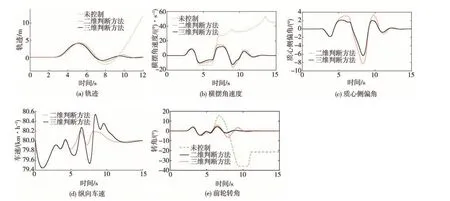
图5 车速80 km/h、附着系数0.3的双移线工况

表2 横摆角速度及质心侧偏角变化幅值(双移线工况,附着系数0.3)
在失稳状态下,纵向车速数据没有意义,故图5(d)中没有进行展示;由图5(e)可见,在无控制情况下,前轮转角甚至达到了结构上的最大值,这在80 km/h的高速下无疑是极其危险的,相对二维判断方法来说,本文给出的三维判断方法可以让前轮转角变化更加平滑,有利于车辆的稳定性。
4.2 附着系数0.8减速避障工况
减速避障工况下,车辆的轨迹、横摆角速度、质心侧偏角、LTR、纵向车速、前轮转角数据如图6 所示。无控制、使用二维相平面判断稳定性、使用三维相空间判断稳定性3 种情况下的横摆角速度、质心侧偏角变化幅值见表3。
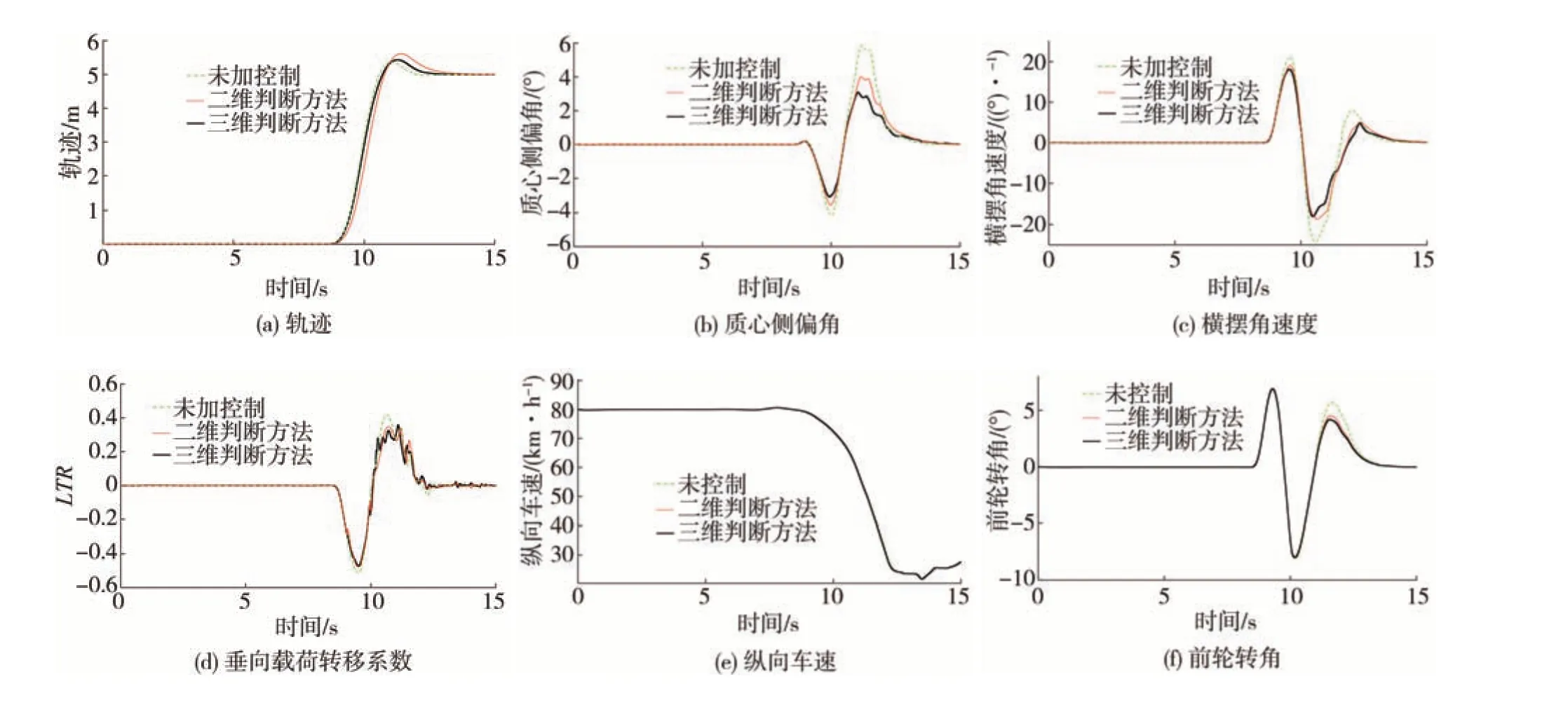
图6 减速避障工况
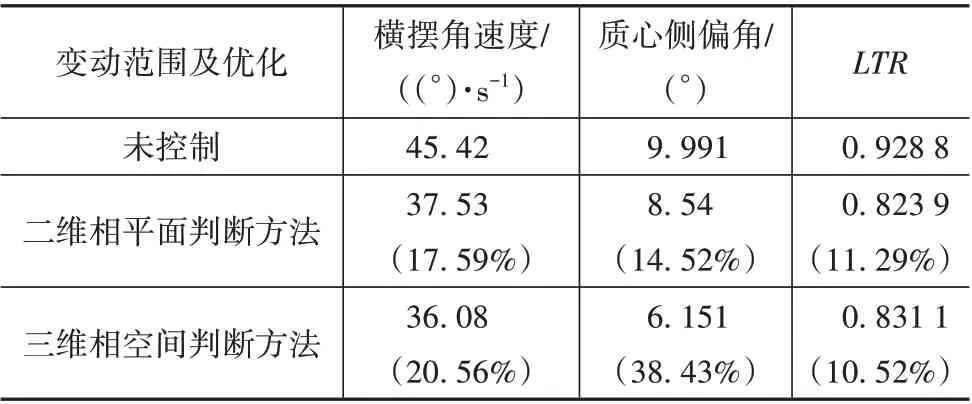
表3 横摆角速度及质心侧偏角变化幅值(减速避障工况)
由图6和表3可知:车辆行驶过程中的横摆角速度和质心侧偏角的变动范围明显减小,车辆的横向稳定极限显著提升;相对于未加控制,车辆的LTR值变动范围略微减小,侧倾稳定性得到一定改善。使用β-ψ̇ -LTR相空间稳定性判断时质心侧偏角改善幅度显著增大,横摆角速度和LTR改善幅度略小,但仍优于β-ψ̇相平面判断的表现。与4.2 节不同的是,车辆在减速避障工况下总体来说并未发生失稳情况,因此是否是加控制并没有对纵向车速、前轮转角产生很大影响,这也很好地符合本文“提升车辆的稳定极限”的思想方针。
5 硬件在环实验
实验采用三轴汽车底盘电控硬件在环综合测试平台,如图7 所示。该测试平台基于东风商用车DFL1250A12 车型,以NI PXI 实时控制器为核心,硬件系统集成了气压制动系统和驾驶模拟器。气压制动系统包括:气压泵、管路、电磁阀、轮毂、制动装置等,驾驶模拟器包括显示屏、座椅、转向盘和电控转向执行器等。该平台可基于TruckSim进行车辆建模并提供多种道路环境,TruckSim 嵌入在Labview RT系统中,为整体测试平台建立上层控制器。DYC/AFS 控制计算得到的制动压力传到制动系统实现制动操作,计算得到的转向盘转角输入到驾驶模拟器中实现转向系统的动作。
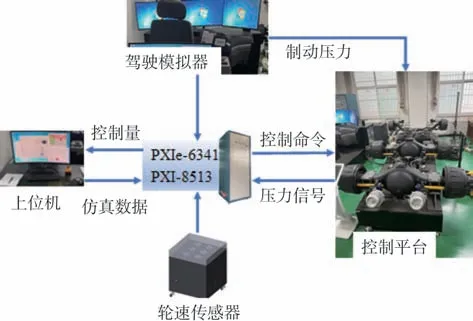
图7 三轴汽车底盘电控综合测试平台硬件关系示意图
硬件在环实验中,NI PXI RT 系统上位机的采样步长设定为0.01 s。采用具有不确定扰动的双移线工况和由国标GB/T38186—2019 规定的紧急避障工况,用于验证控制效果。
5.1 附着系数0.3双移线工况
附着系数0.3 双移线工况实验结果如图8 和表4所示。
由图8 和表4 可见:在未控制时,车辆在转向阶段横摆角速度、质心侧偏角幅值明显大于控制后;控制前后的后轮制动轮缸压力都在允许范围内,说明DYC 控制起到了应有的效果;在双移线工况末尾的直线行驶阶段,未施加控制的横摆角速度、质心侧偏角发生了较大幅度波动,通过施加控制,制动轮缸压力增大,横摆角速度、质心侧偏角的波动明显减小,从而改善了车辆的稳定性。

表4 附着系数0.3双移线工况实验结果
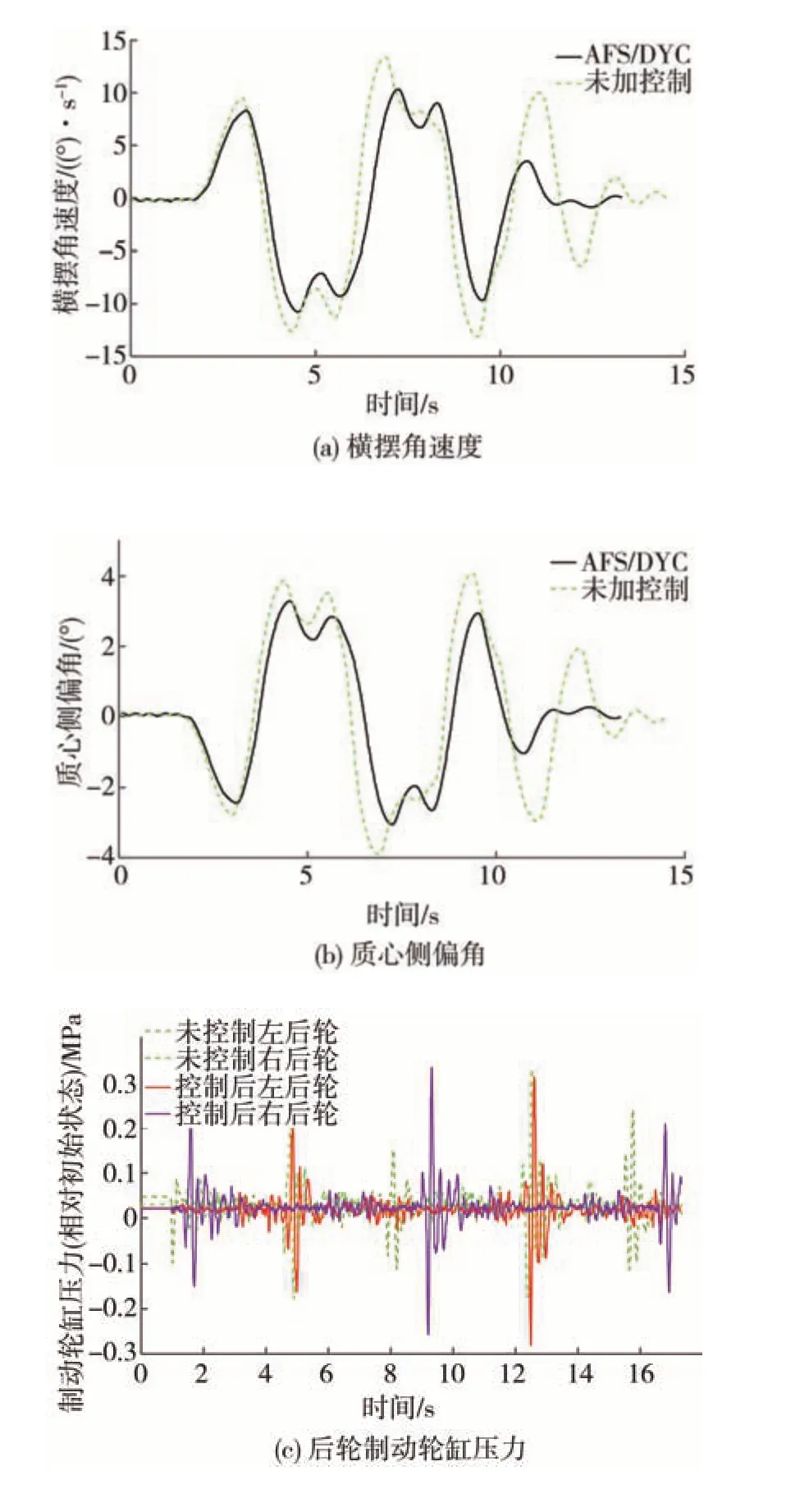
图8 车速80 km/h、附着系数0.3的双移线工况实验结果
5.3 附着系数0.8减速避障工况
附着系数为0.8 的减速避障工况实验结果如图9和表5所示。
由图9和表5可见:车辆行驶过程中并未发生失稳情况,横摆角速度和质心侧偏角的变动幅值减小,但减小幅度小于仿真;相对于未控制,控制后的制动轮缸压力分布和幅值出现了明显改变。
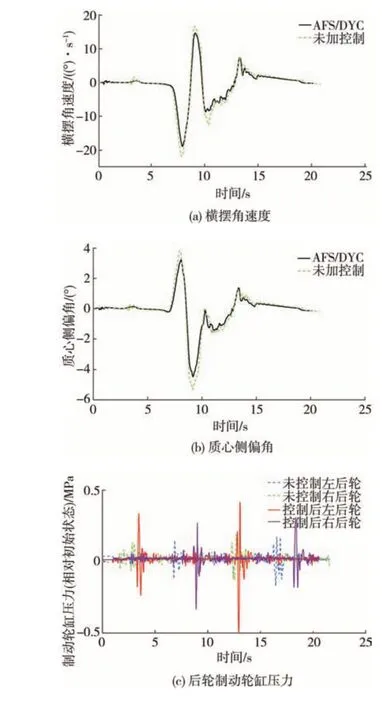
图9 减速避障工况实验结果

表5 减速避障工况实验结果
6 结论
针对重型汽车操纵稳定性提出了基于β-ψ̇ -LTR相空间的车辆横向-横摆-侧倾稳定性判断方法,并设计了基于可拓决策和鲁棒H∞的AFS/DYC分级控制算法。通过TruckSim/Simulink 联合仿真和硬件在环实验,验证了所设计控制算法的有效性。得到如下结论。
(1)在附着力充足的情况下,可拓H∞控制可以保证车辆的质心侧偏角和横摆角速度处于更加安全的范围;其中以在突发状况下或低附着路面时改善效果最佳,横摆角速度优化可达20%;质心侧偏角在仿真中优化接近40%,在硬件在环实验中优化20%,明显优于传统的β-ψ̇相平面稳定性判断方法。
(2)在轮胎接近附着极限的情况下,可拓H∞控制可以起到保证行车轨迹、稳定车辆姿态的作用。
(3)从总体上来看,可拓H∞控制主要保证车辆的质心侧偏角、横摆角速度两个指标,同时在一定程度上参考车辆的侧倾,以保证车辆的横向、横摆、侧倾稳定性,尤为适合低附着路面,并且在突发状况下有足够的响应速度和控制能力。
