A MORE ACCURATE INVESTIGATION INTO THE RELATIONSHIP OF ORIGINAL AIR VOLUME AND PRESSURE WITH CRITICA
2023-04-29ZHUSiyinZHOUShiyun
ZHU Siyin ZHOU Shiyun


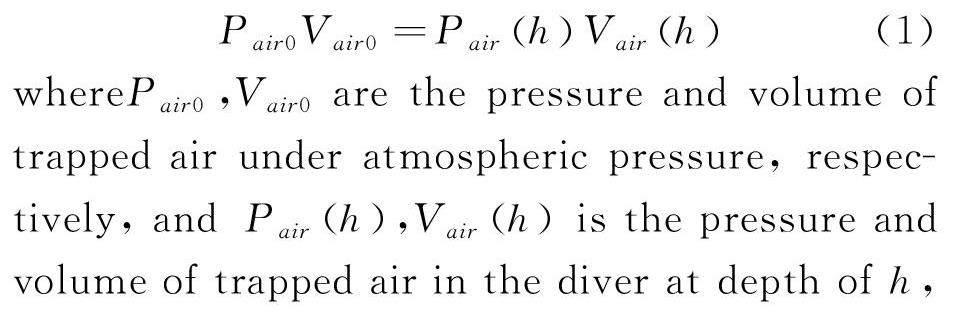
Abstract The purpose of this paper is to investigate the effect of the original air volume andair pressure on the critical depth of the Cartesian diver. Using a transparent cylindrical tube asa container and a plastic tube as the Cartesian diver, the linear relationship between the criticaldepth hc and the volume of trapped air inside the diver Vair0, as well as the linear relationshipbetween the critical depth hc and the initial pressure inside long tube Ptube, were proven. Inorder to improve the accuracy of the experiment, the independent variable of Vair0 must becarefully controlled. Therefore, we focused on the relationship between the critical depth hcand the change of trapped air volume ΔVair0, rather than the original Vair0, thereby improvingthe control accuracy from 1mL to 0.01mL by adding air to the Cartesian diver with a syringe.
Key words Cartesian diver; critical depth; improvement of experimental accuracy
關键词 浮沉子;临界深度;实验精度提高
The Cartesian diver, created as a classic scienceexperiment which proves Archimedes principleand the ideal gas law, is now widely used asa teaching aid[1]. A simple Cartesian diver consistsof a little downward bottle with its lid openand some air trapped in. And the diver flows onthe water surface in a big airtight container almostfilled with water. When we increase thepressure inside the container, such as pressingthe walls of the container, the little bottle sinksfrom the surface of the water. When the pressurechanges back to its initial value, the little bottlemay return or never return to water surface, determinedby the kinematic velocity and depth ofthe Cartesian divers movement when we changethe pressure.
Plenty of apparatuses have been designedand fabricated to demonstrate this phenomenon.To better control and measure the initial pressurein the long tube, a demonstration apparatus wasbuilt with a transparent cylindrical tube and aflange cover connected with a digital manometer[2]. Some others focused on its teaching applicationand made it interesting, like using twokinds of liquids in the large bottle[3] or making itlike a fishing game[4]. There are also articles focusedon dynamic phenomenon, like the Cheerioseffect[5] and the ‘smoke ring phenomenon withwater flowing out[6].
In addition, the most attracting phenomenonis that sometimes the Cartesian diver cant returnto the initial place even though the pressure insidethe container changed back to its initial value.At present, theoretical researches have beendone using the dynamic method[7,8]. Besides, thecalculation of its potential energy has given us abetter understanding of its returning condition[9]. It has been shown that in static equilibrium,the key criterion of divers resurfacing orsinking is whether the divers position reachesthe critical depth, which depends on the initialpressure of the container, the amount of airtrapped inside the diver and the divers ownproperties such as its volume and mass, etc.
However, there are few experimental studieson the parameters affecting the critical depth.Therefore, a set of experimental instruments wasdeveloped, with variables specially designed toaccurately probe the dependence of the criticaldepth on the volume of air trapped in diver andthe initial pressure inside the tube.
1 Models of divers
A transparent cylindrical tube is used as thecontainer and a downward test tube is used as thediver (as shown in Figure 1). There are bothwater and air inside the Cartesian diver at the watersurface. When the pressure inside the tubeincreases, the air volume inside the diver decreasesand the buoyancy declines, resulting in thesinking of the Cartesian diver. When the diversinks to a certain depth, lets discuss whether itwill return to the water surface after returningthe pressure in the tube to its initial value.
To simplify the model, we only consider adiver with solid enclosure. This means that wedo not consider the effect of its shell deformationon the air volume trapped inside. Since the movingof the diver is much slower than the changeof the air volume trapped inside the diver duringits movement, we only need to perform a staticforce analysis to determine its movement trend ata certain depth. Therefore, only gravity, buoy-ancy and surface tension should be consideredand resistance exerted by water can be neglected(as shown in Figure 2). When the Cartesian diverbalances at a certain depth, it will remain motionless.If the diver rests at a shallower place,the air volume in the diver will become larger aswell as the buoyancy, so the diver will go up.With the diver going up, the air volume will increasefurther, so the diver will continue goingup until it reaches the water surface. On the otherhand, if the diver rests at a deeper place, theair volume in the diver will become smaller aswell as the buoyancy, so the diver will go down.
Therefore, the key point is the depth atwhich the buoyancy is equal to the gravity plussurface tension, called the critical depth. If thedivers position exceeds the critical depth afterwe increase the pressure in the tube, it will notbe able to return to the water surface even if theinitial pressure is restored.
Some approximations are made to simplifythe model and calculation for the critical depth.First, air is considered as ideal gas, as our experimentswere done at room temperature and atmosphericpressure. Second, the mass of thetrapped air, which is much smaller than the massof the divers enclosure, is neglected[9].
Using the ideal gas law for trapped air in thediver, we have
2 Experimental Setup
Noticing that the critical depth hc has linearrelationship with Vair0 and Ptube, we can provetheir relationship by experiment. The overall experimentalsetup is shown in Figure 4(a), and the used diver is shown in Figure 4(c).
It is a good way to use a large syringe tocontrol the pressure inside the tube, and to showthe value of pressure with a barometer, as shownin Figure 4(d). As the piston of syringe slides inor out, the air pressure inside the long tube increasesor decreases. If the piston is held in acertain place, the air pressure will remain thesame. In this way we can control Ptube.
