小学数学教学中建构数学模型的问题与对策

□江苏省昆山市玉山镇振华实验小学 夏 菲

随着教育改革的推进，我国的教育理念、模式及方法等都在不断创新和改进。现阶段我国各阶段的数学教学中，也越来越重视学生建模意识与能力的培养与提升。因此，将全新的理念、模式及方法等与数学建模思想结合起来，对于进一步引导学生获得问题解决能力、思维能力，提升学生的数学学习兴趣，极具现实价值。本文以小学数学教学中建构数学模型为切入点，分析了影响当前小学数学教学中建模实践的影响因素，并从五个方面提出了有效对策，以期能够提升当前我国数学教学的效率与质量，推动我国教育改革的发展。

一、小学数学教学中建构数学模型存在的问题

现阶段，我国各小学在落实建模教学过程中，存在的问题主要有以下三点：其一，以课堂知识呈现为主，忽视建模思想的渗透。以小学生解决问题中存在的不足为例：小明获得了6 个苹果，还剩下3 个苹果，原来有多少个苹果？这道题考查的是加法的意义，但是单说提纲，学生就会产生迷茫，究其原因是教师并未让学生建立起明确的加法模型，学生不了解“部分+部分=总量”这一数学模型，因此，本来用6+3 来解决的问题，学生就会在迷茫中用6-3 解决。学生没有强烈的建模思想与意识，就会用错误的方式解决问题。其二，以活动形式结论为主，忽视学习过程的体验。以“圆的周长”部分知识为例，教师在教学中会先引导学生获得周长的测量方法，而在这个过程中，教师会要求学生通过某种方法或工具完成测量，这样的过程看似是让学生自主探究的过程，实际上是一种“强调式”的学习思维，学生最终知识的获得以记忆为主，并非个人通过建模推导获得。因此，数学建模趋于形式化的现象也比较突出。其三，以数学建模拟态为主，忽视与实际生活的关联。以“垂直和平行”为例，教师往往会选用单双杠等体育器具作为教学案例，就单从单双杠的存在来讲，确实是凸显生活化的事物，但学生没有在学习“垂直和平行”部分知识的过程中前往体验和获得，就无法真正将建模思想与知识的现实应用结合起来。因此，教师在建模教学中，还应该尽可能打造可实践性的生活化教学方法，以期强化学生建模意识，引导学生学会建模应用。

二、小学数学教学中建构数学模型的对策

《义务教育数学课程标准（2022 版）》中，将模型思想区分为“模型意识”与“模型观念”两个层次，将数学教学终极目标确定为“会用数学的语言表达世界”，并提出建模思想的构建环节：问题情境—建立模型—解释应用。而在整个建模环节中，建立模型环节无疑是最重要最关键的，也是整个建模的核心，因此，如何有效引导学生建模，是教师亟须研究、实践和解决的问题。

（一）引导学生自主探究，强化学生建模意识

H.Freudenthal 曾经认为，学生完成数学知识学习，唯一正确的、有效的方法就是学生进行自主再创造。换言之，学生要获得数学知识，就需要不断去进行探索和寻找，以便于获得正确的数学问题解决方法。

就以小学数学知识“以分数除以整数”部分为例，教材的要求是引导学生针对以下问题进行探寻和解决：“将一块西瓜的2/3 平均划分为3 份，每一份西瓜是这块西瓜的几分之几？”当教师提出问题后，给予学生一定的时间去思考，先探究题干与问题之间的关系，并分析数据。在此基础上，学生以小组学习的形式进行各种假设并提出以下观点：学生甲认为应让分子2 和分母3 同时除以整数3；学生乙认为应让分子2 除以整数3，分母3 则保持不变；学生丙认为应将2/3 化为小数0.67，再用0.67 除以整数3；学生丁则认为可以用分数2/3 乘以整数3 的倒数，但其中究竟哪种想法是正确的？需要学生进一步去思考和探索。因此，教师需要指导学生进行亲自验证，让学生在具体的操作中得出以下结论：其一，分母3 不变，分子2 除以整数3；其二，求出2/3 的1/3，所以用2/3×3/1；其三，将2/3 化为0.67，由0.67÷3=0.22，0.22=11/50。学生在陆续完成探究的过程中，逐渐发表自己的见解，推翻自我假设，提出新的假设，教师则在此基础上进行继续深入的引导：如果是把这块西瓜的2/3 平分为4 份、5 份，甚至更多，每份是这块西瓜的几分之几？这个过程中的假设、探究、问题解决等环节，从本质上来讲，是学生主动性思维与个性化思维的应用与提升，让学生在算理感知、算法抽象及建模时获得更多经验的积累，对于培养学生的建模意识与建模应用有积极价值。

（二）鼓励学生进行实践操作，培养学生建模习惯

实践操作对于学生而言，是数学学习中极重要的概念构建起点与基础，学生在完成实践操作过程中，不仅需要具备具体的实际操作行为，还需要观察、思考、接受、对比、交流沟通、问题解决等抽象的数学建模能力。

以小学数学知识“平行四边形的面积”部分为例，教师在组织学生进行知识学习和掌握时，首先，需要为学生提供一定的动手操作工具，即大小一致的透明方格纸张、大小一致的平行四边形、剪刀、尺子等，让学生基于现有的工具以不同的方式来计算出手里现有平行四边形的面积。学生了解了教师的要求，明确了教学目的后，会基于纸张、平行四边形等作出如下的假设：学生甲先对方格纸中的方格大小进行测量，再将平行四边形放置于透明方格纸之上，对平行四边形进行描边，然后数一数方格的数量，以此来完成平行四边形面积的计算；学生乙同样对方格纸中的方格大小进行测量，后将平行四边形进行裁剪，裁剪为一个长方形与两个全等三角形，先对长方形进行描边，数格子，计算长方形面积，在对三角形进行拼接描边，计算拼接后长方形的面积，将两个长方形面积加起来，得到平行四边形面积；学生丙观察能力和思维能力更强，直接摒除用格子纸描边数数的计算方法，将平行四边形裁剪拼接为两个长方形，用尺子测量后计算两个长方形面积之和，得到平行四边形面积；学生丁则直接将平行四边形拼接为一个完整的长方形，测量长宽，计算面积，获得平行四边形与长方形之间的关系。在这个过程中，学生通过独立思考、自主操作、小组合作讨论、交流沟通、总结反思等方法，充分、深入地挖掘出了平行四边形面积计算公式的由来及内涵，为学生平行四边形计算公式的建模提供了帮助与引导，这样的实践操作，既有效强化了学生的数学学习思维，激发了学生的思考与探求，也将实践活动的内在价值充分发挥了出来，使学生建模意识和建模应用能力得到了综合性提升。

（三）督促学生交流辨析，培养学生建模能力

任何知识的学习和获得都是充满曲折的过程，不是一帆风顺的，对于小学生而言，培养建模意识、获得建模能力、学会建模应用也是一个连续性的、连贯的、系统且充满挫折的过程，这个过程中，需要学生借助交流沟通发现个中不足，并基于思维碰撞弥补这些不足，同时，也离不开教师的有效引导。

以小学数学知识“小数乘小数”部分为例，学生需要完成以下问题的探究：有一块长2.2 米，宽1.3 米的长方形模板，尝试计算这块模板的面积。教师可以让学生以4 人一组为单位，借助同比例的教学模具完成探索，最终得出结果。而在这个过程中，苹果组的学生认为2.2 米就是22 分米，1.3 米就是13 分米，因此，这块模板的面积是22×13 ＝286 平方分米，由分米换算为米，则这块模板的面积是2.86 平方米；香蕉组的学生认为无论是小数乘法还是整数乘法，都可以通过列竖式的方式来进行计算，因此，直接列竖式22×13即可，此时得到的结果是这块模板的面积是2.86 平方米。教师不必急于对学生作出评价和引导，而是应该采取以下办法：第一步，让每一个组选一名学生作为代表进行发言，说一说本组成员的观点、假设和得出的结论；第二步，让小组成员再一次投入到交流沟通中去，在组内比一比各组解决问题的办法，选出最优或最简练的解决方法；第三步，让学生针对上述观点发表是否认同的看法。这一过程中，有的学生会觉得第一种方法繁杂一些，但结果是正确的；有的学生认为第二种方法看似简练，但是容易忽视小数点……这样交流辨析、活跃的过程，学生可以及时通过假设验证，推翻自我不切实际的假设，去伪存真，真正了解数学建模的价值。再结合教师行之有效的、适当的引导，会让学生更清晰、正确地对数学建模和数学理算进行了解和掌握，让思维碰撞、观点修正为学生的建模意识与应用能力培养提供保障，引导学生自然而然、水到渠成地获得建模思想，从而培养建模能力，提升学生的学数学学习能力。

（四）打造有效评价回顾，引导学生建模意识形成

探究的目的是解决问题，但问题是否解决，离不开后续的有效评价和回顾总结。因此，探究后的评价、反思、总结与回顾等环节，看似并非必要性环节，但在帮助学生记录经验、养成学生建模意识方面的作用也是不容忽视的。

以小学数学知识“三角形内角和”部分中的一道例题为例，如图1 所示，要求学生基于算和画发现题中规律。学生在完成题目计算过程中不难发现：三角形、四边形、五边形乃至n 边形的内角和都可以表示为180°×（n－2）这一数学建模公式。事实上，在此之前，教师都会通过或抽象的、概括的、推理的方式来引导学生来得出180°×（n－2）这一结论，但是这一结论的内涵究竟是什么？如何基于建模思想得出结论？教师并不重视，甚至于诸如“为什么n 边形切割为三角形后，三角形的个数与n 边形边数之间的差距为2”这样的问题也不曾提出，或引发学生进行思考，学生也不了解为什么一个四边形可以切割成两个三角形，一个五边形可以切割成三个三角形。这样的现实状况往往会造成学生难以理解建模思想，甚至无法培养学生的建模意识。但是，如果教师能够组织有效的反思与回顾，就会发现自身教学实践中的不足，进而引导学生参与反思，此时，如果教师再将“为什么将n 边形切割成三角形时，个数比n 边形边数少2”这个问题提出，引发学生思考探究，学生就会再一次去进行学习内容的回归，弥补不足的同时，强化自身的建模意识，进一步了解数学建模的内涵与本质，促进学生数学学科核心素养的综合提升。

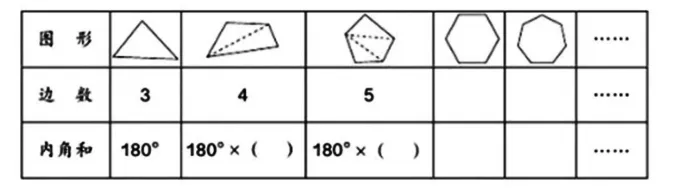
图1

（五）引入生活实例教学，鼓励学生进行建模验证

当人们脱离出学生身份，再以旁观者的角度看待这个身份时会发现，学生最大的不足之处在于，无法正视知识的学以致用。简言之，学生并不理解何为“数学来源于生活”。但是随着教育改革的发展，当前的数学教学越来越强调数学知识的情境化和生活化。因此，教师在落实学生的建模意识培养过程中，需要结合生活实例完成教学知识整合，让学生在具体的数学知识应用中去区分数学现象和数学实力，让学生明确数学结构、数学关系、数学定理、数学性质之间的统一性、相似性与辩证性。当然，教师在引导学生获得全新的数学知识后，也需要留给学生足够的独立空间，让学生自主完成数学知识验证，教师则需给予适度引导，启发学生在验证过程中发现和获得拓展性数学知识，进而自主地创造问题，解决问题，不断地强化自身建模意识，推翻假设、验证假设，得出正确的数学结论，并结合所掌握的数学规律，来解决生活中的数学问题。这一数学模型建构形式，不仅是让学生主动进行数学学习的过程，也是让学生善于发现、勇于创新的过程。

以小学数学应用题中的“植树问题”教学为例：一个圆形池塘周长为400 米，在岸边每隔4 米栽一棵白杨树，一共能栽多少棵白杨树？针对类似问题，教师就可以基于真实的户外环境来进行教学实践，带领学生前往青少年教育培训基地植树，基于基地内的树木引出教学内容和所需解决的问题，或者让学生以小组为单位，在划定的区域内植树。另外，教师还可以基于此类题型，开发其他相关的应用问题，引导学生强化建模意识。比如，让学生以竖向两排为要求进行照明灯安装；让学生在指定面积的住宅内进行地板砖铺设等。使学生基于植树问题来掌握数学知识和现实生活的关系，以便于培养学生的数学建模能力，引导学生构建起数学基础与数学知识现实应用之间的桥梁，让学生在实际操作过程中将数学知识联系于生活、应用于生活，为学生创设现实的学习情境，培养学生的问题解决能力。

三、结语

总而言之，建模意识与能力的培养，是当前我国数学教育改革发展不可或缺的重要部分，值得广大小学数学教师重视、实践与研究，而基于“引导学生自主探究，强化学生建模意识”“鼓励学生实践操作，培养学生建模习惯”“督促学生交流辨析，培养学生建模能力”“打造有效评价回顾，引导学生建模意识形成”“引入生活实例教学，鼓励学生进行建模验证”五个方面的小学数学建模教学问题优化，希望能够提高我国小学数学教学的有效性。