高考全国卷中函数图像问题的考向分析

■江苏省南京市第十三中学 杨红霞

函数图像是函数性质的直观反映,借助函数图像,可以研究许多函数问题,所以函数图像的考查一直是历年高考的重点和热点。常见的题型有:选择图像、研读图像和应用图像。下面举例说明。

一、选择图像

例1(2022届江西上饶二次模拟)函数f(x)=的大致图像为图1 中的( )。

图1

故选B。

评注:此类选择图像问题是指已知函数解析式,定性分析函数的性质,如单调性、奇偶性等,从所给选项中选择出对应的函数图像,这是函数图像问题考查的基本形式。

二、研读图像

例2(2023届安徽皖西联考)牛顿流体符合牛顿黏性定律,在一定温度和剪切速率范围内黏度值是保持恒定的,即τ=ηγ,其中τ为剪切应力,η为黏度,γ为剪切速率;而当液体的剪切应力和剪切速率存在非线性关系时,液体就称为非牛顿流体。非牛顿流体会产生很多非常有趣的现象,如当人陷入沼泽时,越挣扎将会陷得越深;也有很多广泛的应用,如某些高分子聚合物还可以做成“液体防弹衣”。图2 是测得的某几种液体的流变τ-γ曲线,则其中属于沼泽和液体防弹衣所用液体的曲线分别是( )。

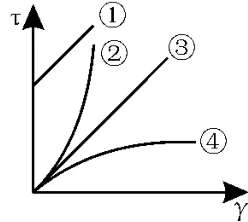
图2

A.③和① B.①和③

C.④和② D.②和④

解析:由题意得牛顿流体黏度η恒定,即在τ-γ曲线中,图像为直线,即①和③为牛顿流体,④和②为非牛顿流体。又因为属于沼泽和液体防弹衣所用液体为非牛顿流体,所以对应曲线为④和②。

故选C。

评注:研读图像要求同学们对所给函数图像进行全方位观察,在此基础上收集信息,研究性质,回答所提出的问题。这是函数图像考查的较高形式。

例3(2023 届湖南长沙一中高三模拟)已知定义在R上的奇函数f(x)的部分图像如图3 所示,f′(x)是f(x)的导函数,则下列结论中正确的是( )。

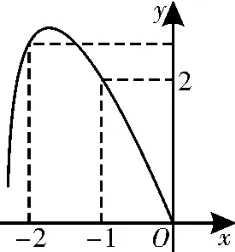
图3

A.f(2)=-1

B.f(1)·f(2)>4

C.f′(1)·f′(2)<0

D.方程f′(x)=0无解

解析:根据题意,依次分析选项:对于A,f(x)为奇函数,且f(-2)>2,则f(2)=-f(-2)<-2,A错误;对于B,f(x)为奇函数,且f(-1)=2,则f(1)=-2,则f(1)f(2)>4,B正确;对于C,由所给函数f(x)的图像,可得f′(-1)<0,f′(-2)>0,所以f′(1)·f′(2)=f′(-1)·f′(-2)<0,C 正确;对于D,由C的结论f′(-1)·f′(-2)<0,则必定存在x0∈(-2,-1),使得f′(x0)=0,即f′(x)=0一定有解,D 错误。

故选BC。

评注:此类题目一定要注意观察图像的特征,看对应函数具有什么性质,比如奇偶性、单调性、对称性、周期性等,还要看图像的最高点、最低点,是否过原点或其他特殊点,与坐标轴的交点等,根据这些特征得出结论。

三、应用图像

例4(2022届四川绵阳第二次模拟)已知函数f(x)=lnx-a(x2-x),若不等式f(x)>0有且仅有2个整数解,则实数a的取值范围为( )。

解析:由题意,f(x)>0有且仅有2个整数解,即lnx-a(x2-x)>0有两个整数解,即lnx>a(x2-x)有两个整数解。令g(x)=lnx,h(x)=a(x2-x)。当a=0 时,lnx>0,即x>1,有无数个整数解,不成立;当a<0时,如图4所示,lnx>a(x2-x)有无数个整数解,不成立;当a>0时,要保证g(x)>h(x)有两个整数解,如图5 所示,则

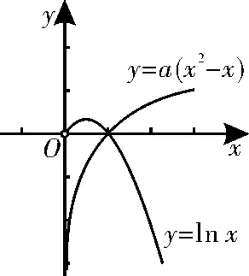
图4

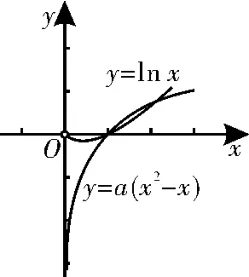
图5

故选A。

评注:应用图像是指善于借助函数的图像这个工具来分析问题、解决问题,实质上就是数形结合思想方法的应用。