随机变量及其分布单元测试卷（A 卷）答案与提示

一、选择题

6.A 提示:因为ξ～B(10,0.4),所以E(ξ)=10×0.4=4,D(ξ)=10×0.4×0.6=2.4。

8.D 提示:A1表示零件来自甲工厂,P(A1)=0.5;A2表示零件来自乙工厂,P(A2)=0.3;A3表示零件来自丙工厂,P(A3)=0.2。

B表示取得的产品为次品,P(B|A1)=0.1,P(B|A2)=0.2,P(B|A1)=0.3。

由P(B)=P(A1)P(B|A1)+P(A2)·P(B|A2)+P(A3)P(B|A3),可得:

P(B)=0.5×0.1+0.3×0.2+0.2×0.3=0.17。

10.C 提示:对于选项A,由图像可得甲地学生的数学平均成绩90 分比乙地的数学平均成绩100分低,故A 错误。

对于选项B,由图像可得甲地学生的数学成绩的离散程度比乙地的大。

对于C,解法一:

若σ2=8,则P(92≤Y≤108)≈0.682 7,P(84≤Y≤116)≈0.954 5,P(76≤Y≤124)≈0.997 3。

对于选项D,由甲地学生成绩的正态曲线的对称性可得,P(90≤X≤94)=P(86≤X≤90)＜P(82≤X≤90),D 错误。

11.C 提示:由题意得,P(A1)=0.5,P(A2)=0.4,P(A3)=0.1。

P(B|A1)=0.9,P(B|A2)=0.9,P(B|A3)=0.8,故A 正确。

P=1-P(B|A1)=1-0.9=0.1,故B正确。

由P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+P(A2)P(B|A2),可得:

P(B)=0.5×0.9+0.4×0.9+0.1×0.8=0.89,故C不正确。

又i∈N,所以i=4,即P0,P1,P2,…,P6中的最大值为P4,选D。

二、填空题

三、解答题

17.设B为取出的零件是次品,A为被挑出零件来自第一箱。

18.(1)Y=2 表示决出冠军需要进行2局比赛,即甲连赢2局或乙连赢2局。

P(Y=2)=0.6×0.6+0.4×0.4=0.52。

(2)若采用3 局2 胜制,不妨设赛满3局,用X表示3 局比赛中甲胜的局数,则X～B(3,0.6)。

甲最终获胜的概率P1=P(X=2)+0.648。

若采用5局3胜制,不妨设赛满5局,用X表示5局比赛中甲胜的局数,则X～B(5,0.6)。

下面计算甲最终获胜的概率:

因为P2＞P1,所以5 局3 胜制对甲有利。

19.(1)设“走L1路线,求最多遇到1 次红灯”为事件A,则A包括没有遇到红灯和只遇到1次红灯的情况。

故Y的分布列如表1。

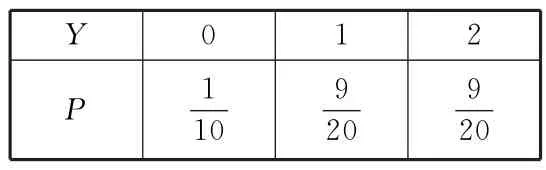
表1

因为E(Y)＜E(X),所以小明选择L2路线最好。

20.(1)由题意可得,X的可能取值为2,3,4,5。

故X的分布列如表2。

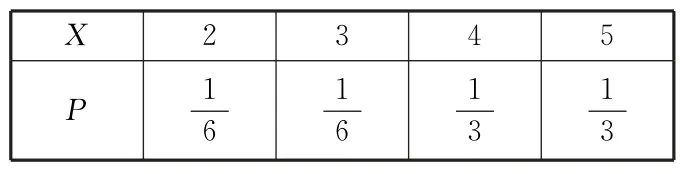
表2

21.(1)质量超过505 g 产品的频率为5×0.05+5×0.01=0.3,所以质量超过505g的产品数量为40×0.3=12(件)。

(2)质量超过505 g 的产品数量为12件,则质量未超过505g 的产品数量为28件,故X服从超几何分布。

故X的分布列如表3。

表3

故Y的分布列如表4。

表4

故随机变量X的分布列如表5。

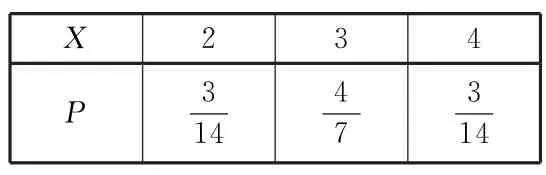
表5

故E(X)=E(Y),于是小明和小宇答对题的平均水平相当。

从正确答题的个数的方差方面分析,小宇成绩发挥比较稳定。

因此,从至少答对3 道题进入决赛的概率方面分析,小宇进入决赛的可能性大。

综上所述,选择小宇参加市级比赛会更好。