价值引领,素养导向,能力为重,知识为基——评析2022年离散型随机变量高考试题

■河南省许昌市胡银伟高中数学名师工作室 胡银伟

2023年伊始,由中国高考报告学术委员会编撰的2023年度高考蓝皮书《中国高考报告(2023)》发布。该报告围绕核心价值、关键能力、情境载体三条主线,指明新高考背景下高考命题的“价值引领、素养导向、能力为重、知识为基”总体要求。报告指出在高考评价体系指导下的高考命题,呈现出“无价值,不入题;无思维,不命题;无情境,不成题”的典型特征。下面我们结合以上三个特征对2022年高考的离散型随机变量试题进行评析。

一、无价值,不入题

2022年离散型随机变量内容的高考命题,紧扣时代主题与时代精神,加强了对学生理想信念、道德品质、奋斗精神、爱国情怀等方面的引导和考查,从而将立德树人这一核心价值融入高考试题中。

例1【2022 年新高考全国Ⅰ卷第20题】一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两类)的关系,在已患该疾病的病例中随机调查了100 例(称为病例组),同时在未患该疾病的人群中随机调查了100例(称为对照组),得到如下数据(表1)。

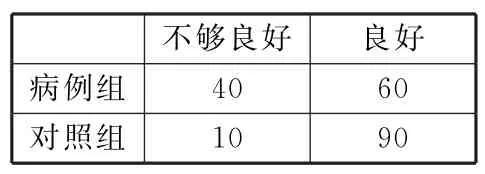
表1

(1)能否有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异?

(2)从该地的人群中任选一人,A表示事件“选到的人卫生习惯不够良好”,B表示事件“选到的人患有该疾病”的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为R。

(ii)利用该调查数据,给出P(A|B),P(A|)的估计值,并利用(i)的结果给出R的估计值。

表2

思路点拨：本题两大问三小问,三个问题层层递进,体现了提出问题、探究问题和解决问题的过程。第(1)问可由所给数据结合公式求出K2的值,将其与临界值比较大小,由此确定:患疾病群体与未患疾病群体的卫生习惯有差异。第(1)问说明卫生习惯会影响患病率,但并没有回答问题:影响程度如何?试题的第(2)问就是为回答此问题而设计的,其中第(i)问为第(ii)问作铺垫,第(i)问根据定义结合条件概率公式即可完成证明;第(ii)问,可根据(i),结合已知数据求出R的值。

解析：(1)由已知条件可得:

又P(K2≥6.635)=0.01,24＞6.635,所以有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异。

试题评析：本题创设出数学探索创新情境和生活实践情境,具有较好的创新性,能很好地体现概率统计知识与方法的应用价值。本题在提高同学们学习统计学知识的兴趣,培养其数学应用意识,提升其解决实际问题的能力等方面都有着积极的引导作用。此外,本题体现了党和国家对人民健康的深切关怀及新时代高考改革的精神,从而体现高考“立德树人、服务选才、引导教学”的核心功能。

二、无思维,不命题

2022年离散型随机变量内容的高考命题,突出了对同学们的关键能力、思维过程和思维品质的考查,从而加强对信息获取与加工、逻辑推理与论证、科学探究与思维建模、批判性思维与创新思维以及语言组织与表达等能力的考查。

例2【2022年新高考全国Ⅱ卷第19题】在某地区进行流行病学调查,随机调查了100位某种疾病患者的年龄,得到的样本数据的频率分布直方图,如图1所示。

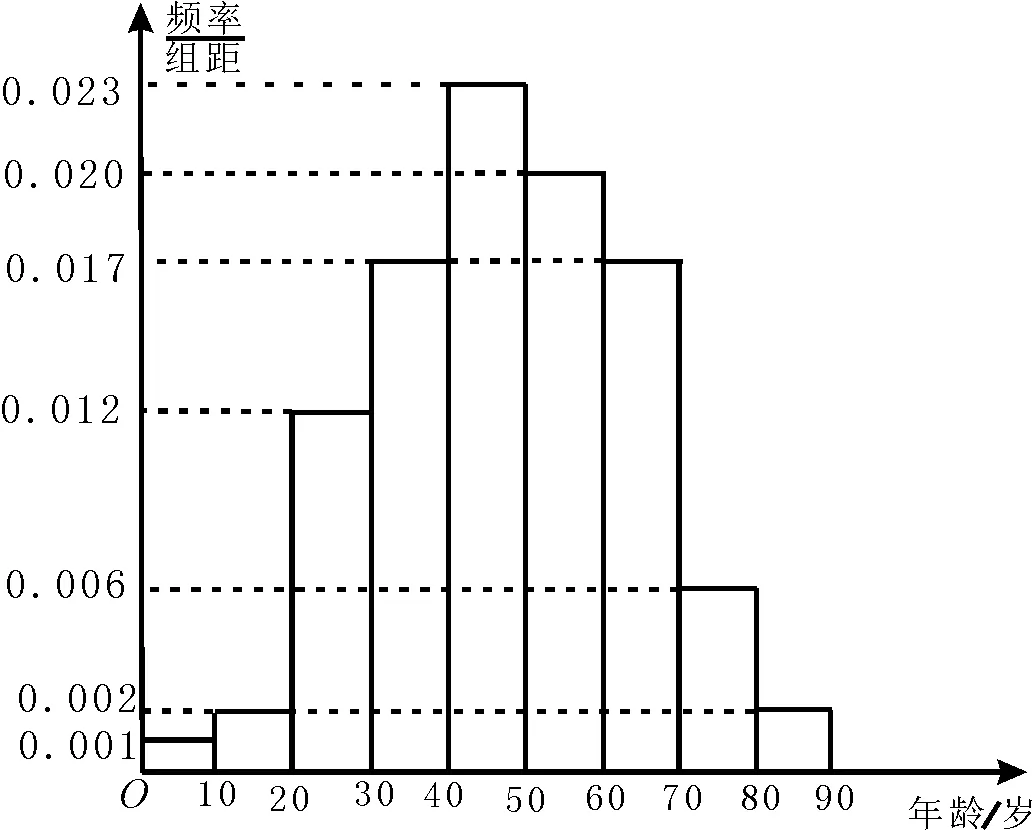
图1

(1)估计该地区这种疾病患者的平均年龄(同一组中的数据用该组区间的中点值为代表)。

(2)估计该地区一位这种疾病患者的年龄位于区间[20,70)的概率。

(3)已知该地区这种疾病的患病率为0.1%,该地区年龄位于区间[40,50)的人口占该地区总人口的16%。从该地区中任选一人,若此人的年龄位于区间[40,50),求此人患这种疾病的概率。(以样本数据中患者的年龄位于各区间的频率作为患者的年龄位于该区间的概率,精确到0.000 1。)

思路点拨：某种疾病患者的年龄分布有何规律? 这是流行病学中需要重点研究的问题。本题以此为情境创设问题,既有现实意义,又能很好地体现数学学科的应用价值。本题考查的内容涉及频率分布直方图、样本估计总体、条件概率等,很好地体现概率统计知识与方法的应用价值。本题的第(1)问可通过对频率分布直方图的解读得所求,第(2)问根据对立事件的概率公式较易解答,第(3)问可根据条件概率公式进行解答。

解析：(1)平均年龄=(5×0.001+15×0.002+25×0.012+35×0.017+45×0.023+55×0.020+65×0.017+75×0.006+85×0.002)×10=47.9(岁)。

(2)设事件A为“一人患这种疾病的年龄在区间[20,70)”。

所以P(A)=1-P()=1-(0.001+0.002+0.006+0.002)×10=1-0.11=0.89。

(3)设事件B为“任选一人年龄位于区间[40,50)”,事件C为“从该地区中任选一人患这种疾病”。

则由已知得,P(B)=16%=0.16,P(C)=0.1%=0.001,P(B|C)=0.023×10=0.23。

试题评析：本题通过创设生活实践情境来考查概率统计的基础知识,问题的解决能很好地体现概率统计知识与方法的应用价值。本题中三问都要求同学们能从频率分布直方图中读出所需的信息,利用频率分布直方图认识和估计总体的分布规律,估计总体的数字特征等。本题有效地考查了同学们的数据处理能力、应用意识和创新能力,考查了大家数学抽象、数学建模等学科素养,同时通过增加思维强度来达成选拔创新人才的目的。

三、无情境,不成题

2022年离散型随机变量内容的高考命题,紧密结合社会热点问题、经济社会发展成就、科学技术进步、生产生活实际等创设真实情境,增强试题的开放性与探究性,从而考查同学们灵活运用所学知识方法发现问题、分析问题和解决实际问题的能力。

例3【2022 年全国乙卷理科卷第10题】某棋手与甲、乙、丙三位棋手各比赛一盘,各盘比赛结果相互独立。已知该棋手与甲、乙、丙比赛获胜的概率分别为p1,p2,p3,且p3＞p2＞p1＞0。记该棋手连胜两盘的概率为p,则( )。

A.p与该棋手和甲、乙、丙的比赛次序无关

B.该棋手在第二盘与甲比赛,p最大

C.该棋手在第二盘与乙比赛,p最大

D.该棋手在第二盘与丙比赛,p最大

思路点拨：本题以同学们熟悉的棋类比赛这一生活实践情境设计概率问题,考查独立条件下多次随机事件发生的概率,是伯努利试验的推广,主要考查同学们对基本独立事件概率的掌握。解答时大家首先要分析、理解比赛规则,再考虑该棋手连胜两盘的各种可能性。该棋手连胜两盘,则第二盘为必胜盘,分别求:该棋手在第二盘与甲比赛且连胜两盘的概率p甲,该棋手在第二盘与乙比赛且连胜两盘的概率p乙,该棋手在第二盘与丙比赛且连胜两盘的概率p丙,并对三者进行比较。

解析：该棋手连胜两盘,则第二盘为必胜盘。记该棋手在第二盘与甲比赛,比赛顺序为乙甲丙、丙甲乙的概率均为,此时连胜两盘的概率为p甲。p1(p2+p3)-2p1p2p3。

记该棋手在第二盘与乙比赛,且连胜两盘的概率为p乙。

则p乙=(1-p1)p2p3+p1p2(1-p3)=p2(p1+p3)-2p1p2p3。

记该棋手在第二盘与丙比赛,且连胜两盘的概率为p丙。

则p丙=(1-p1)p3p2+p1p3(1-p2)=p3(p1+p2)-2p1p2p3。

因为p甲-p乙=p1(p2+p3)-2p1p2p3-[p2(p1+p3)-2p1p2p3]=(p1-p2)p3＜0,并且p乙-p丙=p2(p1+p3)-2p1p2p3-[p3(p1+p2)-2p1p2p3]=(p2-p3)p1＜0,所以p甲＜p乙,p乙＜p丙。

则p与该棋手与甲、乙、丙的比赛次序有关,且该棋手在第二盘与丙比赛时,p最大,故选D。

试题评析：数学源于生活,服务生活,本题以棋类比赛为载体,启发同学们在生活中发现数学问题,并用所学知识来解决问题。本题蕴含的概率思想可以追溯到经典的伯努利试验,本题基于具体问题,易于理解,充分体现了高考命题的创新性。

例4【2022年新高考全国Ⅱ卷第13题】已知随机变量X服从正态分布N(2,σ2),且P(2＜X≤2.5)=0.36,则P(X＞2.5)=____。

思路点拨：本题以正态分布为情境设计问题,正态分布是概率理论与应用中最重要的模型,在数学、物理及工程等领域都有着非常重要的应用,在概率统计学的许多方面有着重大的影响力。本题是考查正态分布随机变量的具体性质与运算,根据正态分布曲线的性质可解答。

解析：因为X～N(2,σ2),所以P(X＜2)=P(X＞2)=0.5。因此,P(X＞2.5)=P(X＞2)-P(2＜X≤2.5)=0.5-0.36=0.14。

试题评析：正态分布作为高中阶段唯一的连续型随机变量的概率分布,也是现实生活中存在最为广泛的随机变量分布。在日常生产生活中,正态分布是刻画常见不确定性的主要工具,如在校学生每人每周的运动时间就近似服从正态分布。

真题演练：

1.【2022年天津卷第13题】52张扑克牌中没有大小王,无放回地抽取两次,则两次都抽到A的概率为____;已知第一次抽到的是A,则第二次抽取A的概率为____。

解析：由题意,设第一次抽到A的事件为B,第二次抽到A的事件为C。

2.【2022 年浙江卷第5 题】现有7 张卡片,分别写上数字1,2,2,3,4,5,6。从这7张卡片中随机抽取3 张,记所抽取卡片上数字的最小值为ξ,则P(ξ=2)=____,E(ξ)=____。

3.【2022 年全国甲卷理科第19 题】甲、乙两个学校进行体育比赛,比赛共设三个项目,每个项目胜方得10分,负方得0分,没有平局。三个项目比赛结束后,总得分高的学校获得冠军。已知甲学校在三个项目中获胜的概率分别为0.5,0.4,0.8,各项目的比赛结果相互独立。

(1)求甲学校获得冠军的概率;

(2)用X表示乙学校的总得分,求X的分布列与期望。

解析：(1)设甲在三个项目中获胜的事件依次记为A,B,C,所以甲学校获得冠军的概率为P=P(ABC)+P()+P()+P()=0.5×0.4×0.8+0.5×0.4×0.8+0.5×0.6×0.8+0.5×0.4×0.2=0.16+0.16+0.24+0.04=0.6。

(2)依题可知,X的可能取值为0,10,20,30。

所以P(X=0)=0.5×0.4×0.8=0.16,P(X=10)=0.5×0.4×0.8+0.5×0.6×0.8+0.5×0.4×0.2=0.44,P(X=20)=0.5×0.6×0.8+0.5×0.4×0.2+0.5×0.6×0.2=0.34,P(X=30)=0.5×0.6×0.2=0.06。

X的分布列如表3。

表3

期望E(X)=0×0.16+10×0.44+20×0.34+30×0.06=13。

4.【2022年北京卷】在校运动会上,只有甲、乙、丙三名同学参加铅球比赛,比赛成绩达到9.50 m 以上(含9.50 m)的同学将获得优秀奖。为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙三名同学以往的比赛成绩,并整理得到如下数据(单位:m):

甲:9.80,9.70,9.55,9.54,9.48,9.42,9.40,9.35,9.30,9.25;

乙:9.78,9.56,9.51,9.36,9.32,9.23;

丙:9.85,9.65,9.20,9.16。

假设用频率估计概率,且甲、乙、丙的比赛成绩相互独立。

(1)估计甲在校运动会铅球比赛中获得优秀奖的概率;

(2)设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数,估计X的数学期望E(X);

(3)在校运动会铅球比赛中,甲、乙、丙谁获得冠军的概率估计值最大? (结论不要求证明)

解析：(1)甲以往的10 次成绩中有4 次获得优秀,由频率估计概率可得甲获得优秀的概率为0.4。

(2)乙获得优秀的概率为0.5,丙获得优秀的概率为0.5,设甲获得优秀为事件A1,乙获得优秀为事件A2,丙获得优秀为事件A3。

X的分布列如表4。

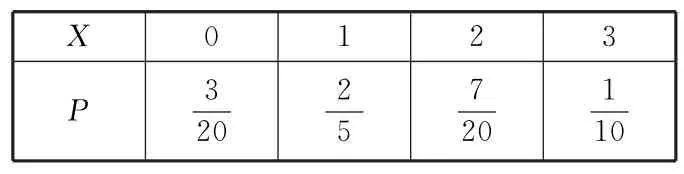
表4