大长径比固体火箭发动机一阶纵向不稳定燃烧判据①

谭智杰,李军伟,张文昊,王宁飞

(北京理工大学 宇航学院,北京 100081)

0 引言

大长径比固体火箭发动机因其推力大、装药量大、续航能力强,在军事、航天运载领域应用广泛。但这类发动机燃烧稳定性往往随工作时间变差,燃烧室内的小扰动振幅容易在工作末期发展为较显著的燃烧不稳定现象,其压力振荡频率较低且往往与燃烧室声腔固有模态低阶轴向频率相近[1-3]。对于这类不稳定燃烧问题,研究人员常常从推进剂的压力耦合响应着手,通过重新选择推进剂或修改发动机局部结构等方式加以解决[4-5]。尽管国内众多高等院校开展的大量理论和实验研究为规避发动机燃烧不稳定现象提供了参考依据[6-12],但大长径比发动机不稳定燃烧往往在项目研制的后期被发现,而此时型号研制主要设计工作基本完成,工程上用以解决不稳定燃烧的措施较少,且受到诸多约束。

本文基于燃烧不稳定线性理论,并考虑发动机结构参数作为设计变量,得到了大长径比、管型内燃药柱固体火箭发动机一阶纵向不稳定燃烧判据,为在设计阶段规避这类不稳定燃烧问题提供参考。

1 基于线性燃烧不稳定理论的固体火箭发动机设计准则

传统的燃烧不稳定线性理论通过计算固体火箭发动机内各项增益和阻尼之代数和,可以获得燃烧室内声能振幅增长率α的数值,进而判断发动机工作过程中的线性稳定性[2-3]。

对图1中的大长径比、管型内燃装药固体火箭发动机,CULICK对基于两相流的雷诺平均方程进行推导,选取燃面压强燃烧响应增益常数αPC、喷管阻尼系数αN、微粒阻尼系数αP来计算判定发动机线性稳定性常数α[13-14]。

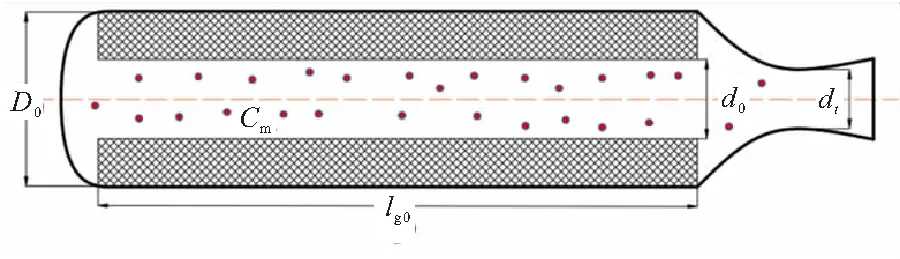
图1 大长径比固体火箭发动机示意图

对大长径比固体火箭发动机,结合声能放大机理以及基于小扰动的一维声波方程,可得轴向振型的燃面压强燃烧响应增益常数为

(1)

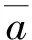
固体火箭发动机燃烧室空腔与封闭的刚性壁圆柱空腔不同,燃烧室的喷管端不是封闭的和刚性的,燃烧室中的声能会以辐射和对流的方式从喷管排出,因而喷管对燃烧室中的声能起到阻尼作用。对轴向振型(即纵向振型),喷管阻尼作用显著。根据CULICK“短喷管”理论[19],假定气流不发生分离、燃气粘性和热传导可忽略且燃气流的滞止压力与滞止温度不随时间和位置变化,可以推导求解喷管阻尼αN:

(2)

式中J为喉通比;ab为固体发动机燃烧室内实际声速并满足

ab=2flc

(3)

式中f为大长径比发动机不稳定燃烧一阶纵向振荡频率。

至于固体火箭发动机线性燃烧不稳定理论中的微粒阻尼,主要是指悬浮在燃气中惰性难溶氧化物颗粒对声能起阻尼作用。这是因为固体推进剂燃烧过程中,其中的铝粉燃烧会生成大量尺寸不一致的Al2O3微粒。工程上估算微粒阻尼的经验公式[21]:

αP≈-0.34fCm

(4)

式中Cm为燃气中微粒质量分数,可由式(5)计算[2-3]。

(5)

式中δ为固体推进剂中所含铝的质量分数。

根据固体发动机不稳定燃烧线性理论,可将固体火箭发动机视为一个声自激振荡器。声场中声扰动在传播过程中受到各种增益和阻尼的影响,会发生声振幅值的改变。在各种阻尼因素中,往往只有喷管阻尼和微粒阻尼大到与燃面增益具有同一数量级,其他阻尼通常比燃面增益小得多[15-16],本研究也仅仅考察燃面增益(压力耦合响应)、喷管阻尼以及微粒阻尼对声振荡的影响。

对增益和各项阻尼进行代数求和,得到图1所示的管型内燃装药、大长径比发动机的线性稳定条件为

αPC+αN+αP<0

(6)

进一步可得到:

(7)

对某工作过程中的固体发动机,进行式(7)的计算即可初步判断该发动机是否处在线性稳定状态,以及是否有保持线性稳定之趋势。

调整式(7)为

(8)

式(8)已经能够初步判定某固体发动机的线性稳定性,但其仍然属于工程上解决已经出现的固体发动机线性不稳定现象问题的判断方法。对于发动机设计而言,追求的目标应该是在设计方案拟定之初就能够判断发动机的线性稳定性。简单研判可知,需要设法消去式(8)中的压力振荡频率f。

将式(3)代入式(1),可得

(9)

对于管型内燃装药,燃烧室自由容积Vc可表达为

Vc=lcSc

(10)

于是可以得到

(11)

整理式(6)～式(11),可以得到

(12)

显然,式(12)适用于设计阶段的固体发动机线性稳定性判断,因为该式右侧的参量在发动机设计过程中是可由设计人员研判选取的。

不妨定义:

(13)

则大长径比固体火箭发动机一阶纵向燃烧线性稳定条件为

(14)

式(14)表明,kb能够反映固体推进剂的燃烧响应特性,并且其数值与具体的固体推进剂种类、发动机实际工作状况条件等有关系。因此,在发动机设计阶段只需结合工程经验、实验数据等初步计算某方案中固体发动机的kb值,即可通过式(14)判断该发动机的一阶纵向线性稳定性。

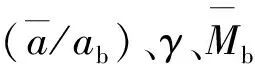
2 大长径比发动机燃烧稳定性变化趋势

式(14)给出了大长径比发动机燃烧线性稳定条件,定义一个判据变量:

(15)

显然,在发动机工作过程中,Aim的值随装药燃面退移而发生变化,也就是随发动机工作时间变化。因此,Aim能够作为判定大长径比发动机工作过程中燃烧线性稳定性的参数。由式(15)可知,在大长径比固体火箭发动机工作过程中,对其燃烧线性稳定性影响较为显著的几个参数有内孔初始直径d0、喷管喉径dt、装药长度lg0、凝相物质百分比Cm、燃烧室直径D0。这些参数与燃面增益、喷管阻尼、颗粒阻尼等影响因素的具体数值密切相关;通过合理选取并修改这些参数、再对式(15)进行计算,就能够得到发动机工作过程中Aim的大小变化,也就能得到大长径比固体火箭发动机一阶纵向线性稳定性变化趋势。具体计算方法为对假定的不同工况计算其燃烧室压强曲线,在此基础上即可获得计算式(15)所需的若干参数。对于燃烧室压强计算过程,考虑丁羟三组元复合推进剂,结合零维内弹道相关计算方法,给出计算所需的推进剂及燃气物性参数如表1所示。在实际工程应用的大长径比固体火箭发动机工作末期,其燃烧室声腔结构逐渐近似于圆柱声腔结构。因此,可以将大长径比固体火箭发动机药柱简化为管型内燃药柱。下面基于这一简化处理,给出计算大长径比发动机线性稳定性变化趋势所需的工况参数如表2所示。结合表2的工况参数对式(15)进行计算,得到药柱内孔直径对燃烧稳定性影响以及燃烧室压强曲线如图2所示。

表1 推进剂及燃气物性参数

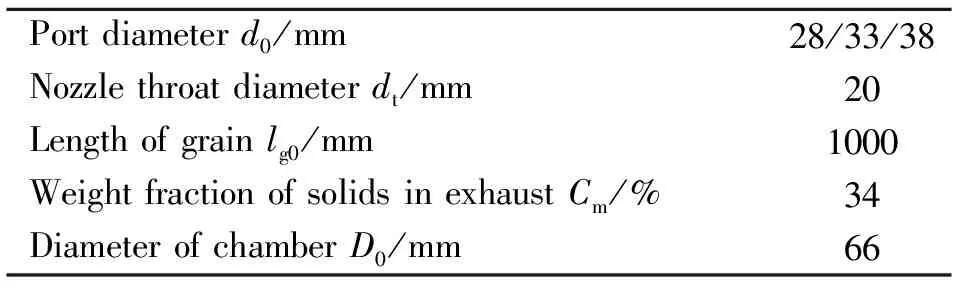
表2 线性稳定趋势计算工况参数

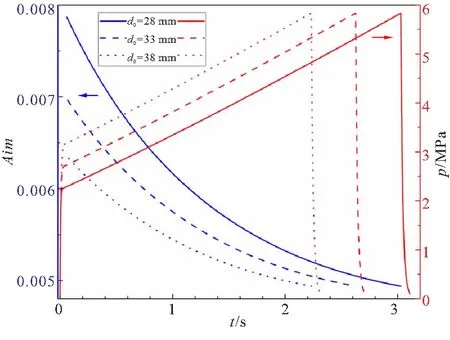
图2 药柱内孔直径对燃烧稳定性的影响

由图2可知,不同药柱内孔直径条件下,Aim的最终值均为0.004 9,也即发动机工作末期的线性稳定性基本一致,这是因为药柱内孔直径未能影响工作末期的燃面增益。

取表2中药柱内孔直径为33 mm,再取不同药柱长度分别为800、1000、1200 mm,保持表2中其他参数不变,得到的计算结果如图3所示。

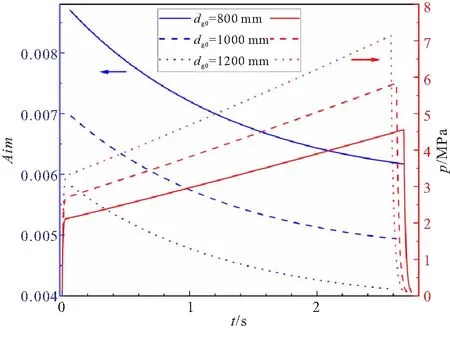
图3 药柱长度对燃烧稳定性的影响

图3表明,任意相同时刻,较大的药柱长度lg0都会带来较小的Aim,即发动机更有可能出现一阶纵向线性不稳定现象。如1.0 s时,药柱长度为1000 mm下的Aim值约为0.005 7,而800 mm和1200 mm的对应Aim值分别为0.007 2和0.004 8;这表示其他条件不变时,增加药柱长度会造成燃面面积提高,导致推进剂燃面向燃烧室内声振荡提供更多的增益,削弱了发动机的线性稳定性。

取表2中药柱内孔直径为33 mm,再取不同凝相百分比分别为为0、0.1、0.2、0.3和0.39,保持表2中其他参数不变,得到的计算结果如图4所示。

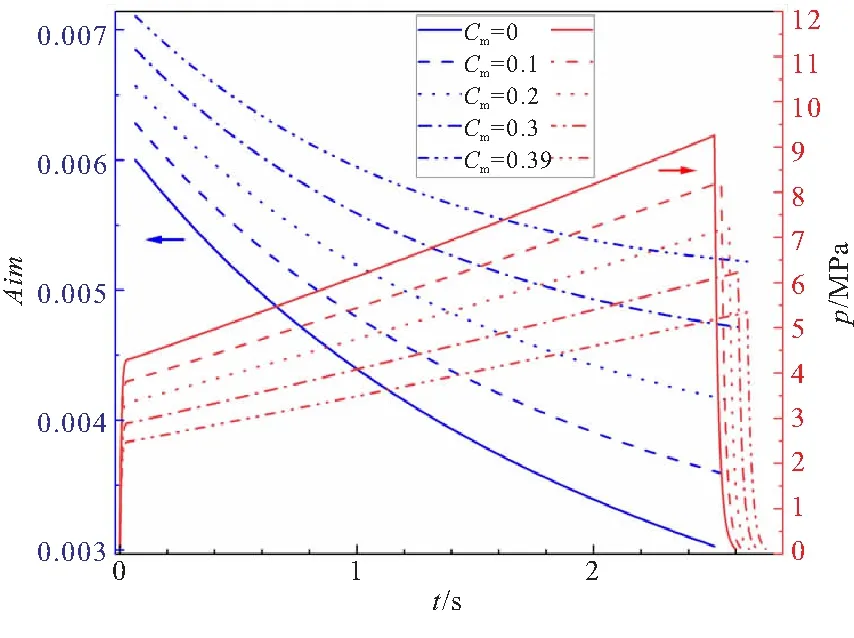
图4 凝相百分比对燃烧稳定性的影响

图4表明,随着凝相百分比的提高,Aim曲线整体向上偏移情况比较显著。当凝相百分比为0,即考虑无凝相工况条件时,Aim的最小值下探至约0.003,较容易发生不稳定燃烧;而当凝相百分比提高至0.39时,Aim的最小值为0.005 2,相比无凝相工况提高了约73.3%。可见,提高发动机的凝相百分比确实能起到增强发动机线性稳定性的作用。

取表2中药柱内孔直径为33 mm,再取不同燃烧室直径分别为61、66、71 mm,保持表2中其他参数不变,得到的计算结果如图5所示。

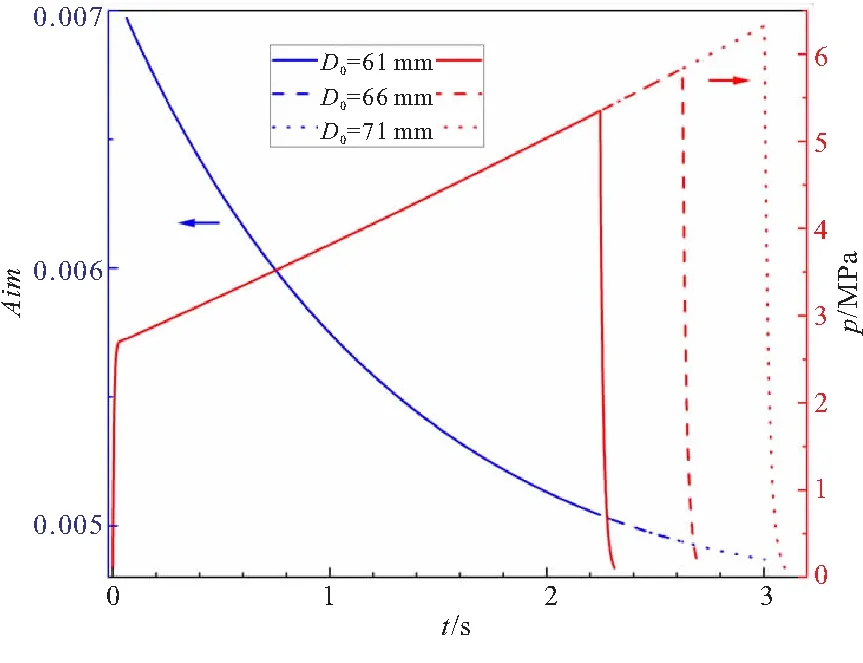
图5 燃烧室直径对燃烧稳定性的影响

图5表明,燃烧室直径D0越大,则发动机工作末期的线性稳定性也越差。这是因为燃烧室直径D0与工作末期的燃面面积关联密切,也就是说更大的燃烧室直径D0往往意味着更大的燃面与更多的声能增益。

结合以上分析可知,影响大长径比发动机稳定性的因素主要是喷管喉径dt、装药长度lg0和凝相物质百分比Cm,而装药内孔直径d0以及燃烧室直径D0的影响往往与其他因素有一定关联,不宜作为独立的影响变量。式(2)表明,喷管喉径dt越大,其所能提供的阻尼也越大,进而对燃烧室内声振荡具有更强的抑制能力;而其他条件不变的情况下,延长装药长度lg0会造成燃面面积大幅度增加,进而为可能发生的声振荡提供更多增益,极大地削弱了发动机保持自身线性稳定性的能力;至于燃气中凝相物质主要通过动力驰豫等机理提供微粒阻尼,简化所得的微粒阻尼计算式(4)表明,凝相物质百分比的提高会增大微粒阻尼的绝对值,进而达到抑制发动机声不稳定燃烧的目标。由此可见,计算式(15)得到的Aim值能够反映大长径比发动机工作过程中增益、阻尼的变化趋势,对燃烧稳定性预估具有一定参考价值。

3 工程实例验证

3.1 验证例一

图6为某大长径比发动机结构示意图,图中各长度单位均为mm。图6中所示发动机的燃烧室主要包括点火座空腔、药柱段及延长段。考虑绝热层的厚度时,燃烧室内径取70 mm,药柱段长度约为508 mm,点火座空腔长度约为50 mm,燃烧室壳体主体与延长段壳体之间为可拆卸结构,且图6中延长段长度为150 mm;该发动机存在两级收敛段,喷管喉径为13 mm。燃面由管型内燃燃面及一侧端燃燃面构成。

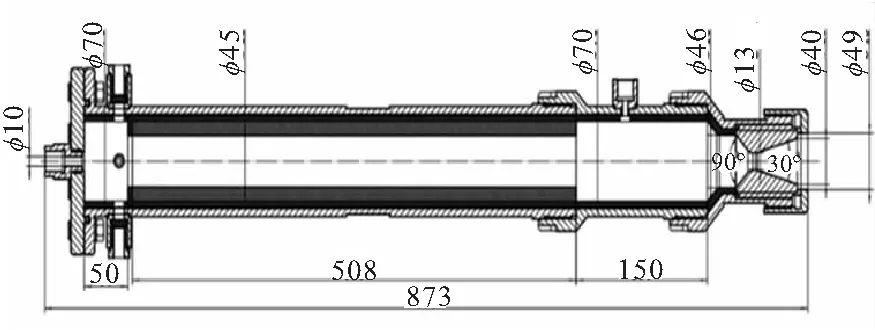
图6 某大长径比发动机结构示意图

为研究大长径比固体发动机的纵向中低频不稳定燃烧现象,本文利用图6发动机开展了一系列地面试验。图7试验中所使用推进剂药柱为丁羟三组元复合推进剂,推进剂及燃气物性参数如表3所示。

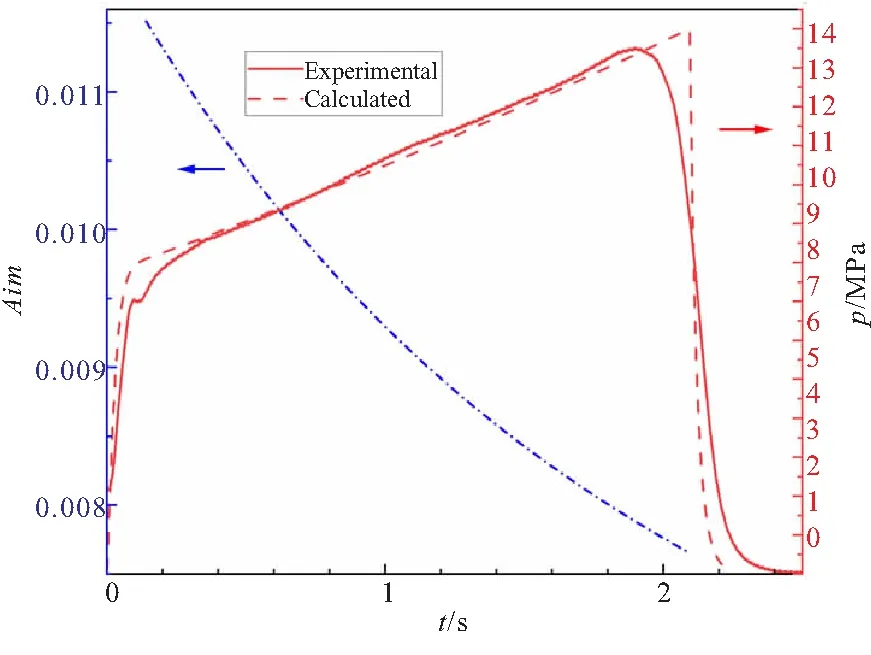
图7 燃烧室压强比对及燃烧稳定性预示

表3 推进剂及燃气物性参数

图7给出了对该次试验中发动机一阶纵向线性稳定性的计算结果,也将计算所得的燃烧室压强与实测数据进行了对比。

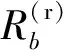
下面考察药柱长度lg0对该大长径比发动机一阶纵向线性稳定性的影响。将图6中延长段撤去,将推进剂药柱长度从原有的508 mm分别延长至708、1108、1508、1908 mm,并相应增加发动机燃烧室壳体长度,且通过调整喉部直径大小的方式来保持燃烧室压强近似不变;之后,依据前文所述方法进行计算,得到燃烧室曲线及燃烧稳定性预示结果如图8所示。图8中,在药柱长度分别为708、1108、1508 mm的条件下,Aim的最小值分别为0.004 5、0.003 6、0.003 2,表明发动机仍能够保持一阶纵向线性稳定。而当药柱长度从lg0从508 mm延长至1908 mm,此时Aim的最小值仅为0.002 9,对比708 mm工况、1108 mm工况、1508 mm工况分别下降了35.56%、19.44%和9.38%。星号标示了药柱长度1908 mm工况中发动机由一阶纵向线性稳定转变为不稳定的临界点,这一转变约发生在点火后2 s,表明此时发动机保持线性稳定的能力较弱,燃烧室内可能出现较为显著的一阶纵向压力振荡现象。

图8 燃烧室压强比对及燃烧稳定性预示-延长药柱

由图8可知,在通过调整喉径保持燃烧室压强近似不变的条件下,增大药柱长度仍能削弱发动机自身保持线性稳定的能力。

3.2 验证例二

为研究药柱结构(或燃烧室构型)与大长径比发动机轴向压力振荡之间的关系,文献[20]利用小型发动机开展了大量不稳定燃烧试验,通过对地面试验所得的压强振荡数据进行对比分析,得到了一些有助于避免不稳定燃烧的工程经验。下面结合试验结果来验证本文所提出的燃烧稳定性判据。

图9为用于研究不稳定燃烧的小型试验发动机结构图。该发动机燃烧室内径为80 mm,喷喉直径为固定值30 mm,可根据不同药柱长度来选取燃烧室壳体长度。如图9所示,这一系列不稳定燃烧试验均采用了管型内燃药柱,通过改变药柱结构参数并开展地面试验、进行数据分析,就可以研究这些因素如何影响发动机的燃烧稳定性。

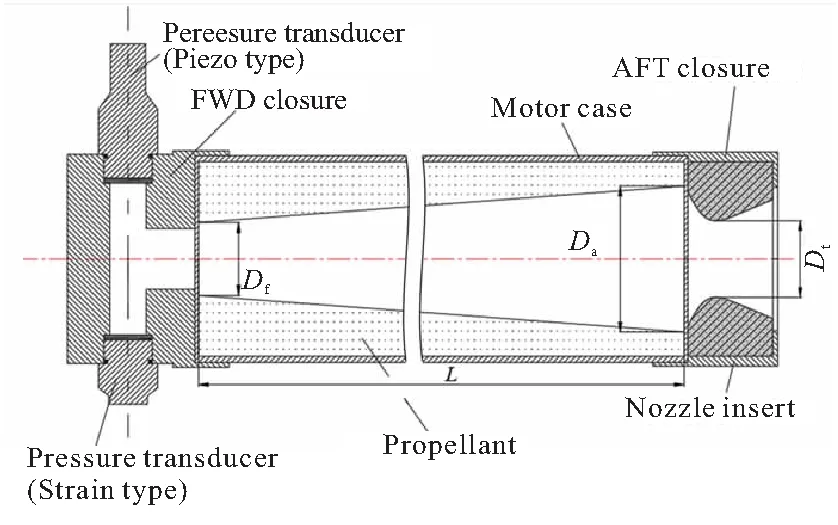
图9 小型试验发动机结构示意[20]

试验中采用的推进剂成分为23%的聚氨酯、67%的高氯酸铵及10%的铝粉[20],药柱整体采用扩孔型燃气通道并辅以小台阶局部结构。为便于分析计算,可忽略小台阶结构的影响,认为燃面为一圆台侧面。给出不同工况的药柱结构参数如表4所示。

表4 药柱结构参数[20]

根据表4所示参数及本文方法,计算得到的燃烧稳定性及燃烧室压强见图10。图10给出了结合文献中试验条件参数对式(15)的计算结果,并在图中标注了计算所得的燃烧不稳定发生时间。通过总结试验数据,研究人员得出这些试验的kb值约为0.011。地面试验数据分析表明,工况Ⅰ、Ⅱ和Ⅲ分别在点火后约1.6、0.75、0.55 s出现较明显的压力振荡现象[20];理论计算估计这三个工况的燃烧不稳定发生时间分别为1.628、0.767、0.52 s,相对误差分别约为1.75%、2.27%、5.45%,符合程度都较好,验证了本文所提出的大长径比固体火箭发动机燃烧稳定性设计判据的适用性。

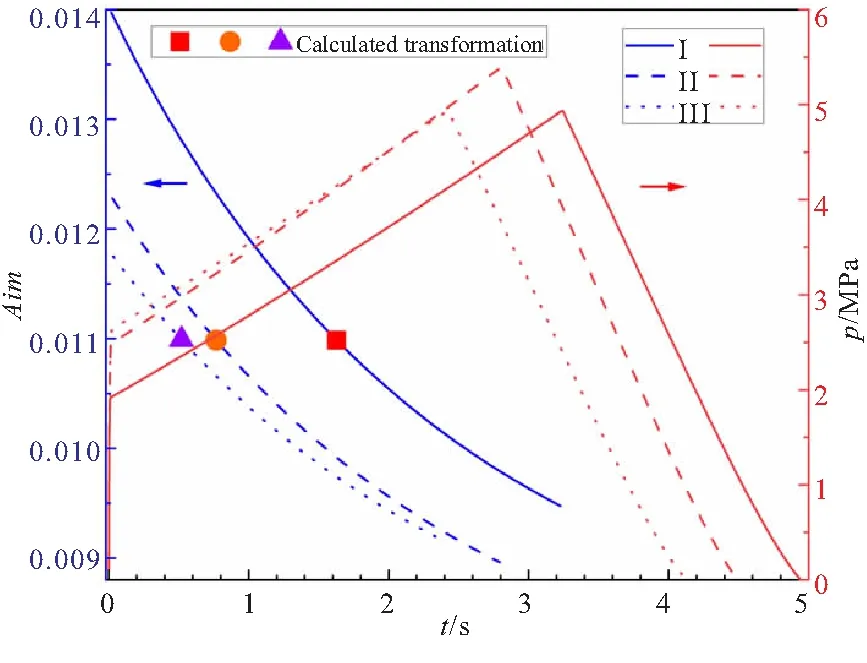
图10 计算所得Aim曲线及燃烧室压强曲线

4 结论

(1)基于固体火箭发动机燃烧不稳定线性理论,主要考虑压强耦合响应、喷管阻尼、微粒阻尼这三项影响因素,提出了可应用于大长径比、管型内燃药柱发动机设计领域的燃烧稳定性设计判据,并运用这一判据计算分析了大长径比发动机设计参数对工作过程中发动机线性稳定性变化趋势的影响。计算结果表明,一定条件下,增大药柱长度会降低发动机线性稳定性,而提高燃气中凝相物质百分比对抑制发动机不稳定燃烧具有一定效果。

(2)利用该燃烧稳定性判据研究了试验发动机中的不稳定燃烧现象,对本文验证例二中小型发动机地面试验的三例不同工况进行计算所得的压力振荡发生时间与试验数据相差不超过6%,表明该判据在大长径比固体火箭发动机燃烧稳定性预测以及大长径比固体火箭发动机设计方面具有一定的参考和应用价值。