结构边界受扰动下翼柱与环槽型固体火箭发动机燃烧室压力振荡特性研究①

陈林君,曹 军,程 书,石 钦,明 爽,郜 冶,侯凯宇

(1.中国航天科技集团有限公司四院四十一所,西安 710025;2.中国航天科技集团有限公司第四研究院,西安 710025;3.哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150000;4.上海航天技术研究院,上海 201100)

0 引言

固体火箭发动机在航空航天领域和导弹武器的发射任务中被广泛使用[1]。为了不断提高固体火箭发动机的性能,一直以来研究人员在设计和优化上付出了许多努力[2-7]。近年来,为了最大限度地提高发动机性能,高能推进剂逐渐成为主流,推进剂的装填系数和发动机的长径比不断提高,这导致固体火箭发动机不稳定燃烧现象频发。而这一类型的发动机具有一些共同特点:发动机的稳定性在整个工作过程会不断变化,往往在外部载荷或内部压强脉冲激发下会出现不稳定燃烧现象。

目前,出现不稳定燃烧的发动机主要有两种:一种是大推力运载火箭采用的固体火箭发动机[8-13];另一种是大长径比的战术固体火箭发动机[14-16]。对于大尺寸的固体火箭发动机而言,产生不稳定燃烧的主要为装药结构复杂的发动机,且多为分段式的发动机。由于装药段之间有绝热挡板,从而易引发流场中出现涡脱落现象,继而与燃烧室声场进行耦合,出现涡-声耦合导致的不稳定燃烧。而对于大长径比的固体火箭发动机不稳定燃烧的形成机理,学术界并未形成统一的定论。有的学者认为不稳定燃烧现象仅由燃烧和声场相互作用引起的[17-18]。近年来,国内大长径比的固体火箭发动机发生的不稳定燃烧现象主要特征是燃烧室内的压力振荡可以达到几百千帕,而导弹结构振动的振幅从发动机开始向全弹逐步减弱,且结构振动的频率为燃烧室声腔基频或者倍频,这一现象可以认为燃烧室内的流动同结构发生了相互耦合振动加强的现象。根据学者们的研究,结构振动的参与可以使燃烧室内的压力振荡幅值达到几百千帕[19-20]。因此,在分析不稳定燃烧中需要考虑结构振动所起到的作用。

从已有的研究成果来看,很少有学者从结构振动和燃烧室内压力振荡相结合的角度对不稳定燃烧开展研究。因此,本文结合发动机结构瞬态响应、推进剂燃速以及燃烧室流场流动,对固体火箭发动机在受结构振动激励扰动下燃烧室内压力振荡特性进行研究,目的在于从结构振动和燃烧室压力振荡相互作用的角度去理解不稳定燃烧形成的机理和过程。从而为设计人员在分析不稳定燃烧现象产生原因以及寻找抑制不稳定燃烧现象的方法时提供理论指导。这对解决我国近年来大长径比的战术导弹固体火箭发动机的不稳定燃烧频发的现象[14],加快研究进程具有重要的工程指导价值。

1 数值模型

1.1 推进剂燃速模型

根据GREATRIX等的研究[21],推进剂表面的径向加速度会对推进剂的燃速产生显著的影响,因而GREATRIX根据实验数据提出了一种用于描述推进剂燃速受加速度影响的模型。该模型的基本原理是:认为加速度提供了压缩燃烧区域的作用,特别是在高密度、低流速接近凝聚相分解层的区域,这是法向加速度能够增大推进剂燃速的主要作用机理。下面给出燃速计算模型:

(1)

式中cp为燃气比定压热容,J/(kg·K);Tf为火焰温度,K;Ts为推进剂表面温度,K;cs为推进剂比热容,J/(kg·K);ΔHs为推进剂表面热释放量,J/kg;Ti为推进剂初始温度,K;ρs为推进剂密度,kg/m3;rb为推进剂总燃速,m/s;λ为燃气热导率,W/(m·K)。

能量参考层厚度δ0和加速度质量流Ga的表达式如下:

(2)

(3)

其中,R为特定气体常数,J/(kg·K);an燃面为法向加速度,m/s2;r0为推进剂基础燃速,m/s;φd为方向角,其表达式如下:

(4)

式中al为切向加速度,m/s2;K为比例系数。

需要注意的是,本文的燃速模型中假设:当加速度的方向指向推进剂表面时,an为负值。根据实验可知[22],当加速度的方向背离推进剂燃面时,对燃速不起作用,因此最终可使推进剂燃速在径向振荡加速度作用下具有净增加值。为了求解受加速度影响的燃速,根据燃面附近的流体参数和燃面的结构振动加速度对式(1)～式(4)进行迭代求解。上述计算模型中的各参数值保持同GREATRIX等的研究中相一致[21]。

1.2 结构边界受扰动下固体火箭发动机燃烧室振荡压强计算模型

燃烧室在实际的工作过程中会由于边界受到扰动产生压力振荡现象,而结构振动激励对燃烧室内流场的边界扰动起到了重要的作用。为了计算燃烧室压力在结构激励作用下的振荡特性,需要将推进剂的燃速和结构的振动相耦合,即计算域中的质量流率入口受结构振动的影响。结构振动对推进剂的燃速影响表现为燃速受推进剂内表面结构振动加速度的作用,这一点已经在1.1节中给出了半经验计算公式。因此,在实际的计算中需要知道推进剂内表面的结构振动加速度,同时燃烧室内表面的压力波动载荷对结构振动的计算来说同样重要。为了节省计算资源,且保证计算网格具有足够的密度,本文的流体计算和瞬态动力学计算中均使用了二维轴对称模型。所以,本文提出了一套计算模型用以支持二维模型的流固耦合计算,图1所示为本文设计的计算方法的流程示意图。

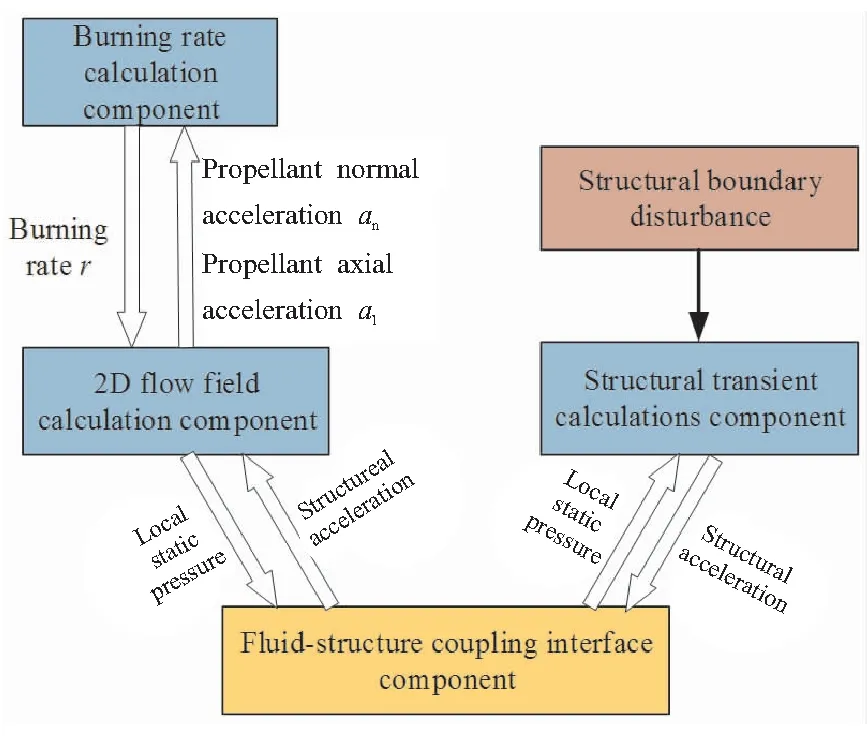
图1 计算模型流程图

本文中的结构载荷作用到发动机结构后通过瞬态动力学计算模块计算得到燃面表面的加速度,然后通过推进剂燃速计算模型得到对应的燃速,并以此计算质量流率,从而实现将过载激励引入计算中以及流场压力振荡和结构振动相耦合的过程。

为了简化计算,本文设计的流固耦合计算模型为弱耦合,即流固交界面之间的位移没有联系,只在交界面上进行加速度和压强这两组数据的相互传递。同时,本文的研究思路为状态凝固化,即取发动机在整个工作过程中特定的几个时刻的模型进行瞬态数值模拟,且在整个计算过程中计算域的网格不发生变化。除此之外,发动机的推进剂在整个过程中受压强和结构振荡而产生的变形对发动机内流场的影响可以忽略。在每个求解时间步,每个计算模块均执行一遍,流固耦合数据交换模块在每个求解时间步提取必要的信息用以流场计算和瞬态动力学模块计算时边界条件的设置。

流固耦合数据交换模块主要负责对流场计算输出的压强和结构计算输出的加速度进行线性插值,这一点对于本文非共节点的两套网格之间的数据交换来说是十分必要的。假设流体网格和结构网格在发动机轴向方向上两节点之间的间距分别为ΔxFI和ΔxSI。设流体网格的节点为i-1、i、i+1,结构网格的节点为j-1、j、j+1,如图2所示,显示了流固耦合交界面网格示意图。则根据流场计算模块得到的燃面表面的压强p可得到结构网格中节点j的压强pj计算公式如式(5)所示。同样,对于结构网格输出的加速度值也是采用和上述相类似的方法进行插值,计算公式如式(6)所示。

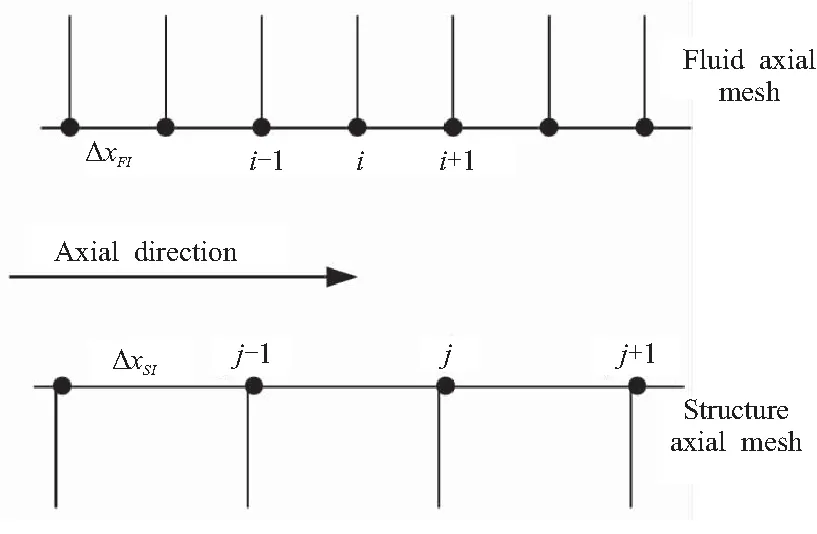
图2 流固耦合交界面网格示意图

(5)

(6)

2 数值计算与结果分析

不同厚度的推进剂(即固体火箭发动机处于不同的工作时刻)对结构振动的传递有不同的特性,所以研究不同工作时刻下发动机燃烧室受激励作用下压力振荡特性是十分必要的。本文选取了翼柱和环向开槽两种燃烧室的三个典型工作时刻的结构和流场模型进行计算,从而对翼柱型和环向开槽型装药燃烧室在结构激励作用下的压力振荡特性进行分析研究。

2.1 计算模型及边界条件

为了后文表述方便,将发动机的工作时间做无量纲化处理:

Tn=ta/td

(7)

式中Tn为无量纲工作时间;ta为发动机实际工作时刻,s;td为发动机总工作时长,s。

本文中选取了翼柱型和环向开槽型装药燃烧室三个典型无量纲工作时刻Tn=0.4、0.6、0.8的内流场和结构模型进行计算,其中内流场的几何模型和边界条件如图3所示。可以看出,从Tn=0.4时刻开始,翼柱装药的尾部翼槽特征已经消失,燃烧室尾部变为突扩结构,燃烧室几何为旋转轴对称几何,因此可以将燃烧室的三维结构简化为二维轴对称模型,而环向开槽装药燃烧室本身就是旋转轴对称几何,故同样可将三维燃烧室简化为二维进行计算。

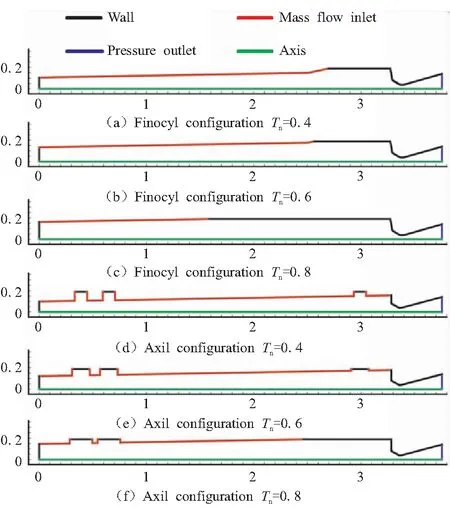
图3 燃烧室内流场几何与边界条件示意图(m)

图4为翼柱和环向开槽装药发动机的结构及部分计算边界条件二维示意图。图中绿色部分为发动机装药,发动机壳体的厚度为5 mm,为图中的灰色部分。图中红色线表示燃烧室的内压载荷加载边界,为燃烧室的内表面。在每个计算时间步输出流场计算中得到的燃烧室内表面的压力,用于瞬态结构动力学计算。对发动机头部的轴向自由度进行了约束,这一约束同其在实际的工作过程的力学边界条件相同。壳体和推进剂的材料力学参数见表1,燃烧室内流场计算中燃气的物性参数见表2。时间步长为1×10-5s,燃烧室中注入的燃气总温为3158 K。

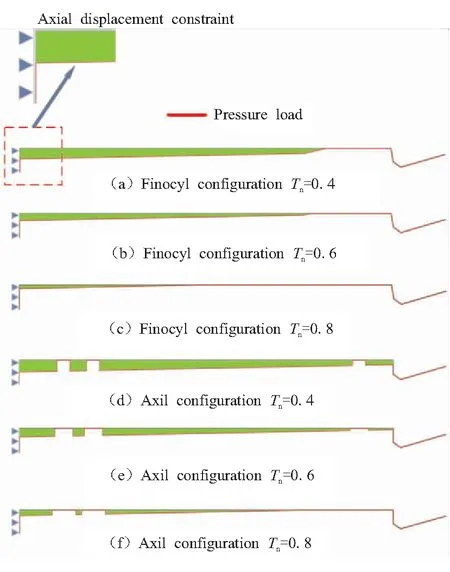
图4 翼柱和环向开槽装药发动机二维结构和边界条件

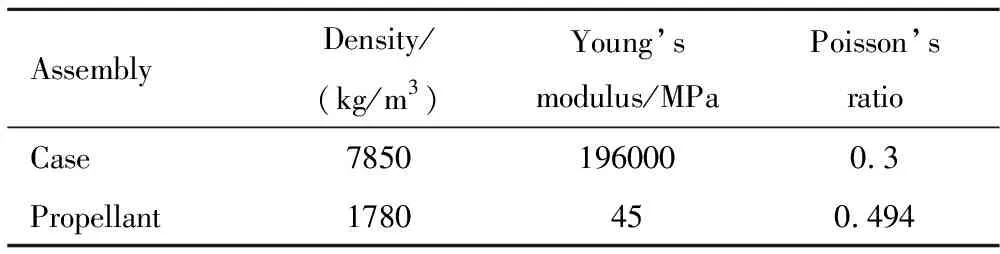
表1 不同结构组件材料属性

表2 燃气物性参数

流场计算中,壁面边界为无滑移的绝热壁面,这是因为固体推进剂的导热系数较低,加之固体火箭发动机工作时间较短,在整个工作过程中可以将燃烧室内表面视作绝热壁面。喷管出口为压力出口,只要出口处压力与燃烧室内压力满足临界条件,出口处的流动就能够达到超音速流,出口的压力并不会对燃烧室内的压力产生任何影响,故出口压力取10 kPa。燃烧室的入口为质量流率入口,单位面积上的质量注入量的计算式为

根据前文中的燃速计算模型对受推进剂表面结构振动加速度作用下的燃速进行计算,从而实现结构激励对燃烧室内压力振荡的影响,具体计算流程如图1所示。本文中流场计算使用的是k-εRNG湍流模型,结构计算中使用的是ANSYS APDL中的二维单元SOLID273,并设置单元KEYOPT(2)=9,即环向有9个节点平面。

本文中施加的结构激励为脉冲作用的加速度载荷。加速度载荷大小为80g,0.01 s后停止施加。各个时刻的流场先使用稳态求解器进行计算以快速得到稳定的流场,稳态计算的收敛判断条件为:(1)压力监测点的压力波动小于0.1%;(2)计算域中入口和出口的质量流量差值波动量小于0.1%。在得到稳态计算收敛的流场后进行瞬态计算,计算0.1 s后得到用于结构激励作用下燃烧室压力振荡特性计算的初始流场。结构计算的时间步长同流场计算中保持一致。为了监测燃烧室中的压力振荡特性,从头部到喷管入口处等距离取31个监测点,所有监测点在一条直线上,离旋转对称轴的径向距离为0.017 m。为了监测发动机的结构振动特性,在燃烧室壳体外表面上从头到尾等间距取20个监测点。最终,将各测点的数据进行FFT,得到对应的频谱数据进行分析。

2.2 流场计算部分网格敏感性验证

为了选择合适的网格尺寸进行计算,必须进行网格尺寸敏感性的验证。使用翼柱装药发动机在无量纲时间Tn=0.4的燃烧室流场模型,如图3所示。计算了三种不同尺寸的网格(表3)在经历脉冲压力后,燃烧室内压力振荡衰减数据。并将计算结果进行处理,通过对比振荡衰减压力的相位、幅值衰减特性和幅值频域特性等三方面,来验证计算网格的敏感性。

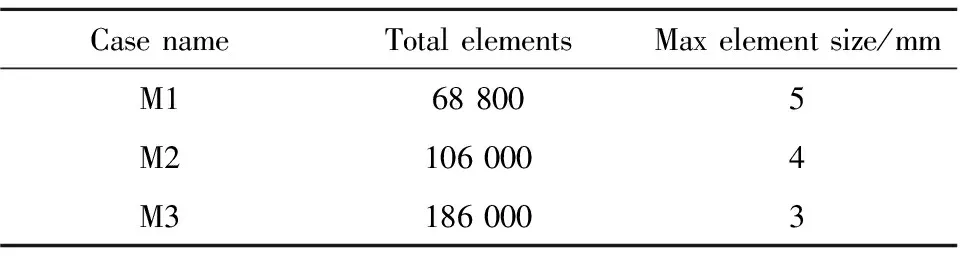
表3 网格验证工况列表

计算中使用的燃气参数如表2所示,计算域入口的质量流率为13 kg/(s·m2),总温T0=3158 K,喷管出口的边界条件为压力出口,模型的最下方为旋转轴对称边界条件,模型的其他边界均为无滑移绝热壁面边界条件,时间步长为1×10-5s。计算10 000个时间步后,对燃烧室头部位置施加压力脉冲。将燃烧室头部壁面的无滑移壁面边界条件改为压力入口,phead=20 MPa。计算50个时间步长之后,停止施加压力脉冲,重新将燃烧室头部壁面改回无滑移壁面的边界条件继续求解。

燃烧室在受到脉冲作用之后,计算中设立的两个监测点的压力振荡情况如图5所示。可以看出,三种不同尺寸的网格对压力脉冲衰减特性的反应能保证较好的一致性。三种网格对于point-1和point-2的压力振荡的相位相差180°左右,这是由这两个点的轴向位置决定的。且由于脉冲从燃烧室头部到喷管喉部的传递过程中,流体的流动会受到壁面以及流体自身的阻尼作用,在振荡幅值上会有所衰减,所以point-1的压强振荡幅值会比point-2高。三种网格反应出的上述脉冲后燃烧室流力振荡的特征均符合物理规律,但在振荡压力衰减率以及压力振幅频谱图上有所差异。

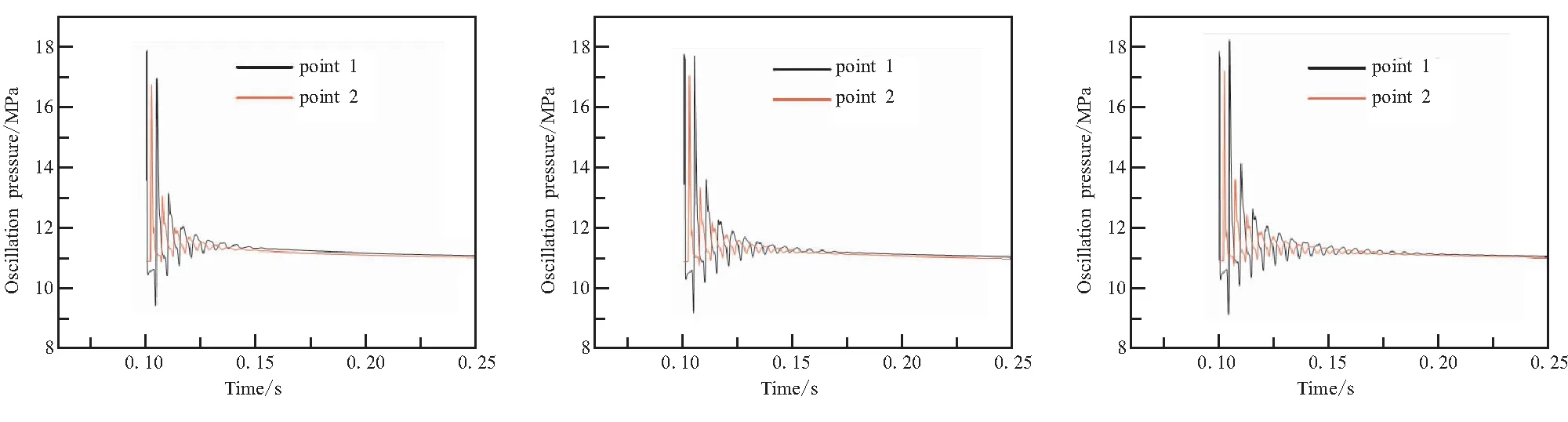
(a)M1 (b)M2 (c)M3

图6所示为三种网格point-1和point-2的压力振荡曲线的上包络线。可以看出,在脉冲施加后的压力衰减初期,两个监测点的压力振幅衰减率较大,这是由于燃烧室内的压力振荡为非线性过程,其流场中存在的突变几何结构的非线性阻尼与压力振荡幅值相关,压力振幅越大阻尼也就越大[23]。三种工况的压力振幅衰减曲线均具有较好的一致性,但在衰减的初始阶段,可以看出不同网格之间的衰减率相同,但其幅值有所差异,随着网格数量的增多,幅值有所增大,这是由于粗网格计算得到的湍流耗散率相对于实际情况会偏大,因此提高网格的密度,能够更精确地计算出压力衰减过程中的振幅振荡衰减特性。

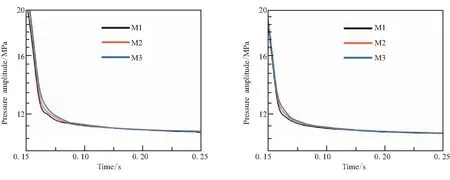
(a)point-1 (b)point-2

为了对比三种尺寸的网格在于压力振荡频域上的计算表现,对两个监测点的振荡压力做快速傅里叶变换,得到压强的均方根(RMS)振幅频谱图,如图7所示。从结果可知,三种尺寸的网格在压力振荡峰值频率上具有良好的一致性,前三阶峰值频率分别为172.5、365、586.7 Hz。这与燃烧室前三阶声频相接近,第一阶压力振荡幅值最大,且尖峰表现地最为陡峭,这表明这一阶的压力振荡能量是最集中的。可见,这三种不同尺度的网格均能在压力振荡频域上有良好表现,计算结果能很好地符合实际物理规律。

(a)point-1 (b)point-2

综合三种网格的计算结果在燃烧室受脉冲作用后在振荡衰减压力的相位、幅值衰减特性和幅值频域特性上的表现,三种尺度的网格均能得到符合物理规律的有效结果。在压力衰减规律上表现较为一致;在压力振荡幅值的计算上,M1～M3依次表现为幅值增大,但三者之间的差别不是很大。网格敏感性的验证在于探究网格数量对于计算结果的影响,由于网格数量越大,计算量也就越大,因此不断提高网格密度是不现实的。故在综合考虑计算量和计算结果精度的情况下,本文后续的计算中将使用M3工况网格的尺度用于计算,即最大网格尺寸为3 mm。

2.3 结构计算部分网格敏感性验证

为了验证网格尺寸对结构瞬态响应的影响,需要开展网格无关性验证。用于验证的模型为翼柱型装药发动机在Tn=0.4的模型,对发动机的头部进行轴向位移约束,在计算初始时刻在发动机的内表面施加阶跃压强,大小为10 MPa。本文对三种不同尺寸的网格的计算结果进行了对比。三种网格分别命名为粗网格、中等网格、细网格,具体网格尺寸如表4所示。

表4 网格无关性验证各工况参数

本验证中取发动机头部的推进剂内表面作为监测位置,选取从加载阶跃压强载荷(即计算初时时刻)开始到0.4×10-2s这一段时间内监测点位移随时间变化的数据作为对比,计算结果如图8所示。从图8中可以看出,三种网格的计算结果具有很好的重合性,这说明此时网格已经收敛。因此,考虑到计算量和结果的精确性,本文结构瞬态响应计算中的网格尺寸将和中等网格保持相一致。

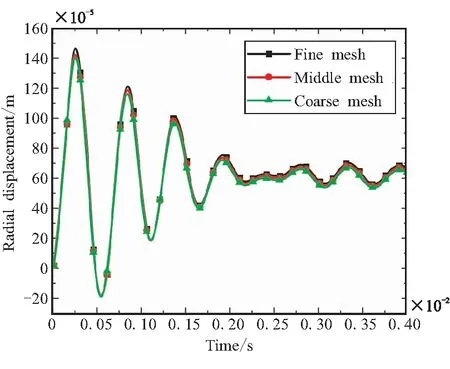
图8 发动机头部推进剂内表面径向位移

2.4 结构边界受扰动下燃烧室振荡压强计算模型验证

为了验证本文计算模型的有效性,设计了相关实验进行验证,根据固体火箭发动机的实际情况,将燃烧室简化为圆柱管腔,为模拟真实的固体火箭发动机,从外到内分别布置壳体(结构钢)、类橡胶材料(用于模拟推进剂),最终搭建出实验装置。

固体火箭发动机燃烧室实际工作过程中为高温高压的环境,对于实施本文的实验是不可行的,学术界对燃烧室声压振荡的研究都是建立在冷流的基础上,而对发动机结构振动的研究也是以未工作时的发动机为对象进行的。因此,本实验对固体火箭发动机进行了一定的简化,为实验的开展进行了一定的假设。首先,实验中假设燃烧室内的流动是静止的。其次,本实验将发动机燃烧室简化为两端封堵的圆柱管腔进行,且在一端使用扬声器进行激励,用以模拟燃烧室中自发产生的压力波动。实验装置如图9所示。选择10 mm厚度橡胶的定频声激励实验数据同计算结果进行对比验证。如图10为10 mm圆柱管腔的计算域示意图,整个计算模型为旋转轴对称。如图11所示,左侧一小块红色区域的网格为激励区,动量源项的变化频率保持和实验中扬声器激励频率一致,为102 Hz。计算中流体的材料为空气,其中密度由理想气体状态方程计算得到。除了旋转对称边界条件以外,其他边界均为无滑移绝热壁面。离散格式为二阶迎风,时间步长为1×10-5s。首先使用瞬态求解器进行流场部分的计算,直到管腔中的压强出现周期性的振荡,然后启动瞬态结构动力学计算,在每个时间步将流场中管腔内表面的压力分布输出作为结构计算下一个时间步的载荷输入,如此反复迭代计算1 s后停止计算,并对得到的数据进行FFT变化,得到振动频域上的信息,同实验值进行对比。

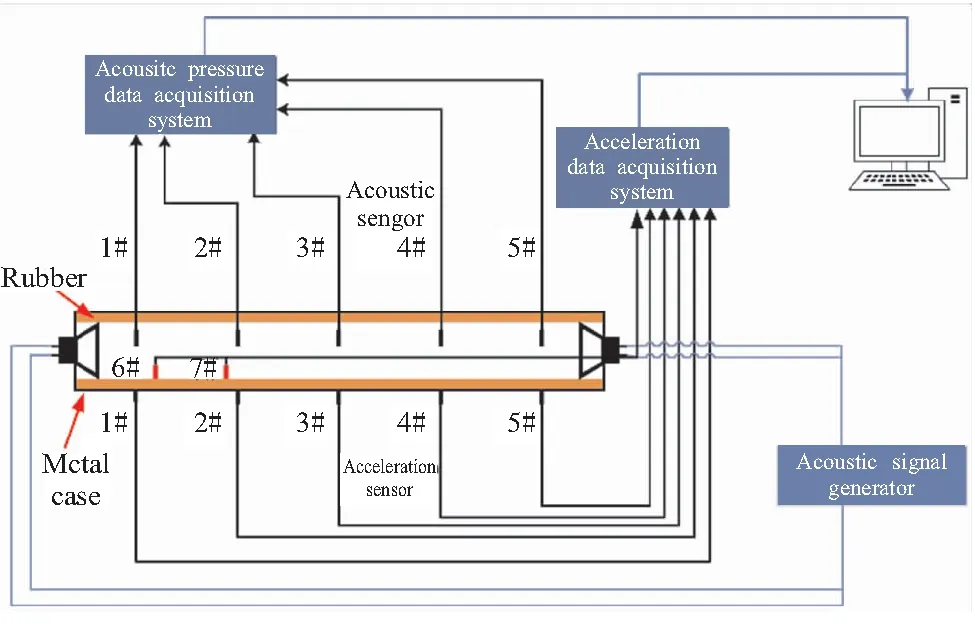
图9 实验系统图

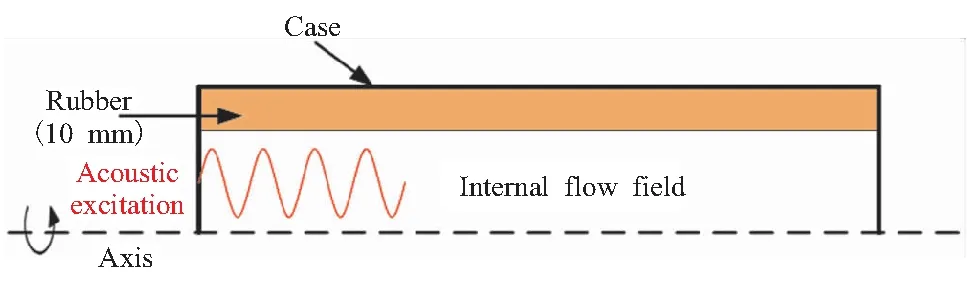
图10 验证计算模型示意图

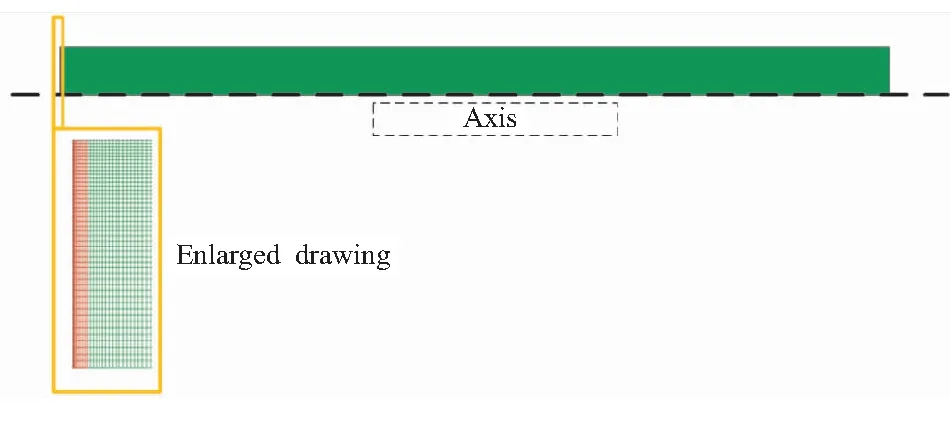
图11 圆柱管腔内流场二维旋转轴对称网格

图12为圆柱管腔外壳测点3和测点5处的实验和数值计算结果的结构振动加速度振幅频谱图。从图中可以看出,数值计算结果和实验结果在102、203、306 Hz处均有一致的峰值存在,数值计算值的振幅相对于实验值来说要高一些,同时实验中高阶频率的峰值更不明显,这可能是由于实验中存在的系统阻尼以及数值计算中并不能保证系统边界条件同实验中完全一致造成的。但从整体结果上来看,数值计算的结果同实验结果吻合性较高,这说明本文提出的用于二维旋转轴对称模型的弱流固耦合计算方法是合理且有效的。

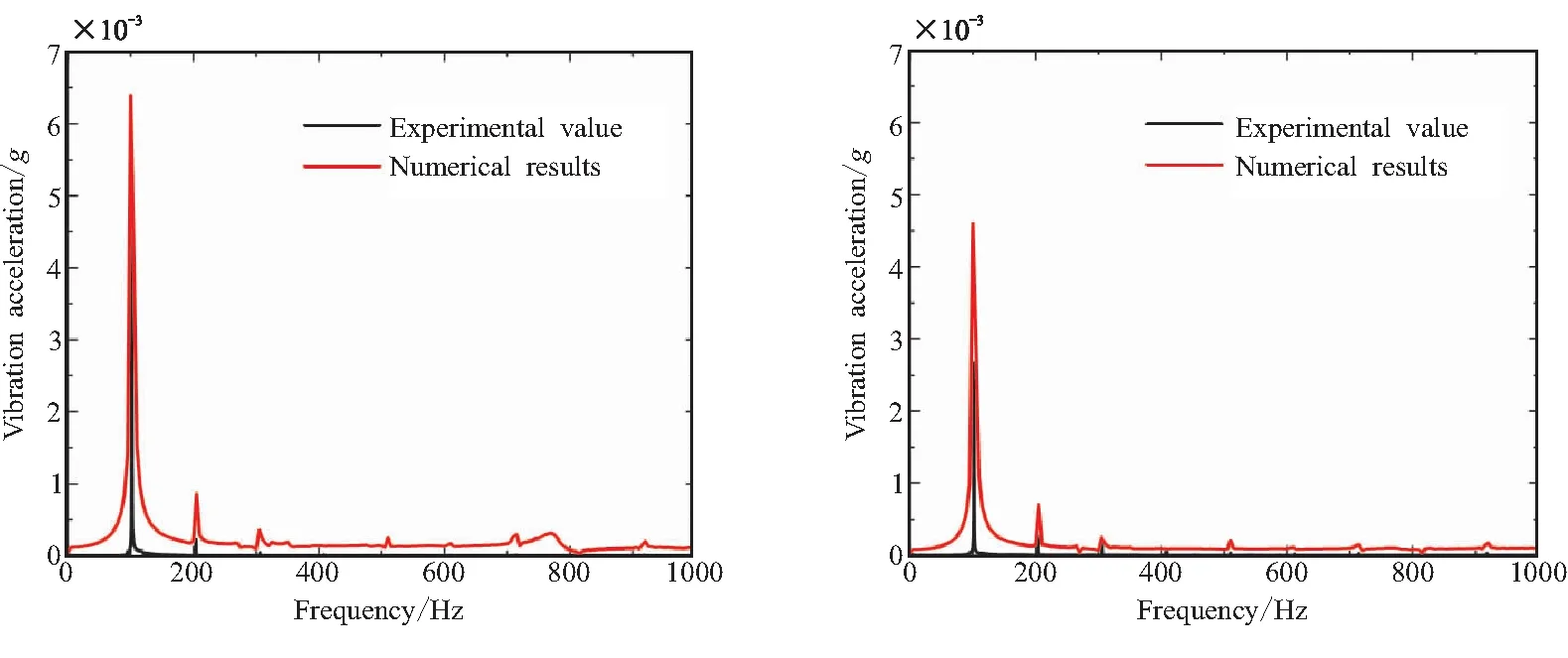
(a)point-3 (b)point-5

2.5 计算结果及讨论

为了便于对固体火箭发动机燃烧室在结构边界受扰动下的压力振荡特性开展分析,本文对翼柱和环向开槽装药的整个工作过程中的结构固有频率、声腔频率进行了计算。由于本文的研究目的之一就是燃烧室压力振荡频率在整个工作过程中是否会同结构固有频率相接近,从而导致两种振动相互加强。而燃烧室内流场计算中压力振荡的各阶频率与燃烧室声学有限元计算得到的各阶声模态频率相接近。因此,对于结构固有频率的关注重点就是在发动机燃烧室一阶、二阶声频附近的振型。对于燃烧室来说,其声腔自发振荡能量主要集中在燃烧室一阶和二阶声频,尤其是一阶声频[24]。对于结构振动来说,弯曲振型不会影响燃烧室内声腔的压力振荡,因为其改变的是轴向尺寸;而呼吸模态能够改变燃烧径向和周向的尺寸,因此对推进剂燃速起到影响,从而能够影响到燃烧室的压力波动。

综上所述,本部分主要关心在燃烧室一阶声频附近的呼吸模态,故这里给出的是发动机燃烧室不同工作时刻的呼吸模态频率和一、二阶声腔频率的变化情况。翼柱装药、环向开槽装药发动机的呼吸模态频率和燃烧室前两阶声频随工作时间的变化曲线如图13所示。

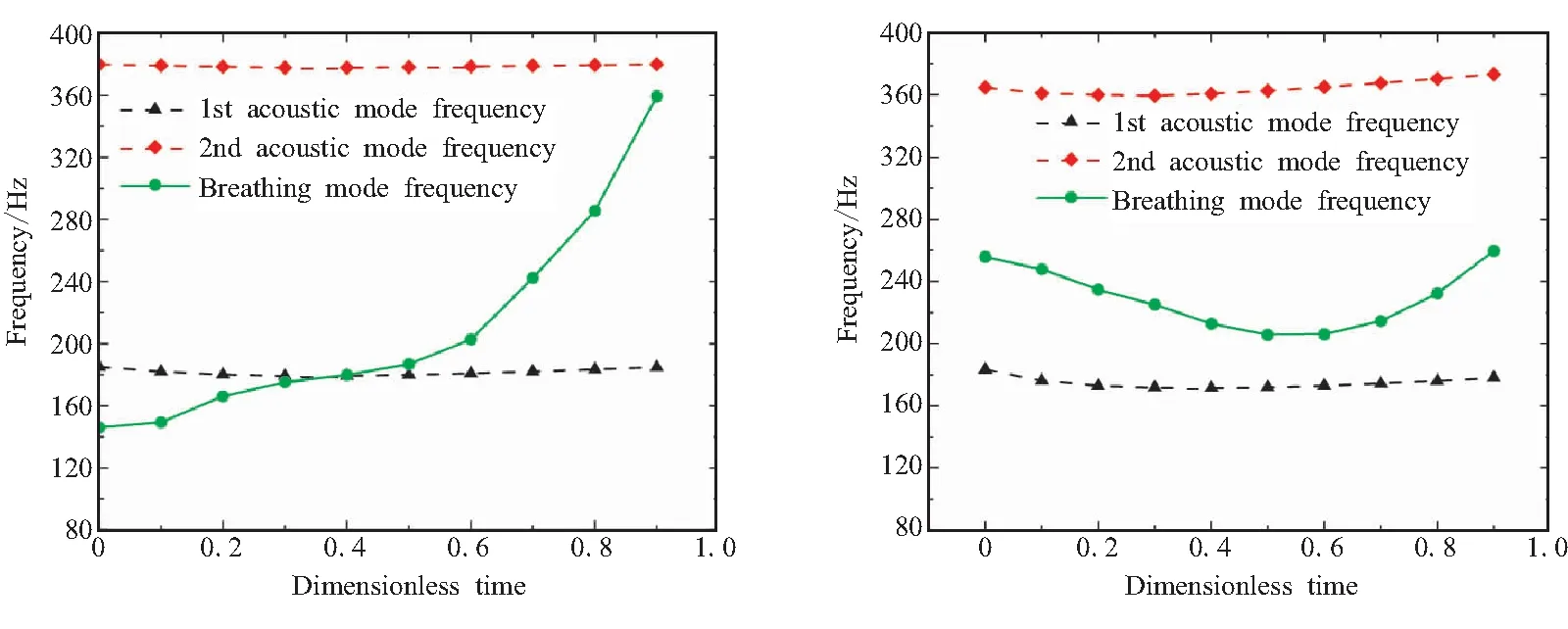
(a)Finocyl configuration motor (b)Axil configuration motor

由图13(a)可以看出,随着工作时间的增长,发动机的装药量不断减小,其呼吸模态出现频率也在不断地升高,可见发动机结构的质量对其振型频率起到了决定性作用。呼吸模态的振动频率的变化范围为工作初期的140 Hz到工作末期的320 Hz左右。在无量纲工作时刻Tn=0.4,该呼吸模态频率与一阶声模态频率相交,整个工作过程中这一振型的频率曲线穿越了一阶声频。由图13(b)可知,呼吸模态频率先减小后增大,在工作的前中期,其频率随装药质量减少而减小的现象更明显,从初始时刻的255 Hz到工作末期的259 Hz,整个工作过程中没有同发动机燃烧室的一阶和二阶声频相交。从图13中可以看出,随着工作时间的增长,呼吸模态的频率不再随发动机装药质量的减少而增大,这一点同翼柱装药发动机有着明显的差别。

翼柱装药燃烧室Tn=0.4、Tn=0.6、Tn=0.8时刻的不同轴向位置测点的压强频谱图如图14所示。从图14(a)中可以明显看出,在受结构脉冲加速度激励后,燃烧室中产生了持续的压强振荡现象,且以一阶声频下的振荡为主,频率为180.4 Hz;二阶声频下的振荡强度相对来说就要小很多,其频率为360.7 Hz。从图中压强振荡幅值随轴向位置的变化规律可以看出,燃烧室内的压强波动表现为明显的驻波特性,同燃烧室声模态振型相符合。具体表现为其一阶振型两端为波峰,中间为波节,故燃烧室两端的振幅高,中间波节处的振幅基本为0;其二阶振型中存在3个波峰,2个波节。由于燃烧室内的压强振荡会在喷管的喉部发生反射,因此对于压强振荡来说实际波动传播的长度还需要加上喷管的扩张段,这也就导致图中一阶声频下的振型的波节位置位于燃烧室中间略靠后处。同时由于燃烧室靠近喷管附近的流体流动速度比燃烧室前端要大,导致此处非定常特征更加突出,这就使得尾部的压强振幅要低于头部。此外,翼柱装药燃烧室的尾部存在突扩的空腔,这一几何结构对压强的振荡具有阻尼作用,同样降低了尾部的压强振幅。一阶振型中头部测点的压强振幅为71.7 kPa,尾部测点的压强振幅为27.5 kPa,头部测点压强振幅是尾部的261%。

由图14(b)可见,同Tn=0.4时刻的计算结果相似,Tn=0.6时刻燃烧室中一阶声模态下的振荡是最为强烈的,二阶声模态下的振荡幅度则要小得多,压强振幅在轴向位置上分布同燃烧室的声模态振型相一致。一阶声模态的压强振荡频率为182.2 Hz,二阶声模态的振荡频率为364.4 Hz。从图中可知,燃烧室的压强振幅较Tn=0.4时刻出现了降低。Tn=0.6时刻燃烧室头部压强振幅为49.4 kPa,尾部压强振幅为28.7 kPa,头部测点压强振幅是尾部的172%,头部压强的振幅强度同尾部之间的差距进一步减小。由此可见,与Tn=0.4时刻相比,主要是燃烧室头部的压强振荡强度出现了降低。根据图13的翼柱装药发动机不同工作时刻的呼吸模态频率变化规律可知,在Tn=0.4时刻其呼吸模态的频率为179.4 Hz,同燃烧室的一阶声频相接近,这就使得压强振荡同结构振动之间出现了相互耦合加强的现象,两者的振动得到了相互增强,而燃烧室尾部的压强振荡由于流速较大导致的强烈的非定常特性以及燃烧室突扩空腔的声阻尼作用使得其压强振幅并没有出现显著变化。而Tn=0.6时刻的呼吸模态频率为202.7 Hz,远离了燃烧室的一阶声模态频率,这也就使得无法出现耦合振动的现象,压强的振荡强度出现了降低,尽管Tn=0.6时刻的燃面面积大于Tn=0.4时刻,即燃烧室内单位时间注入的总扰动能量Tn=0.6时刻更高。可见,燃烧室声频同结构的呼吸模态振动频率是否相接近是决定燃烧室发生不稳定燃烧现象时压强振荡强度的重要因素。

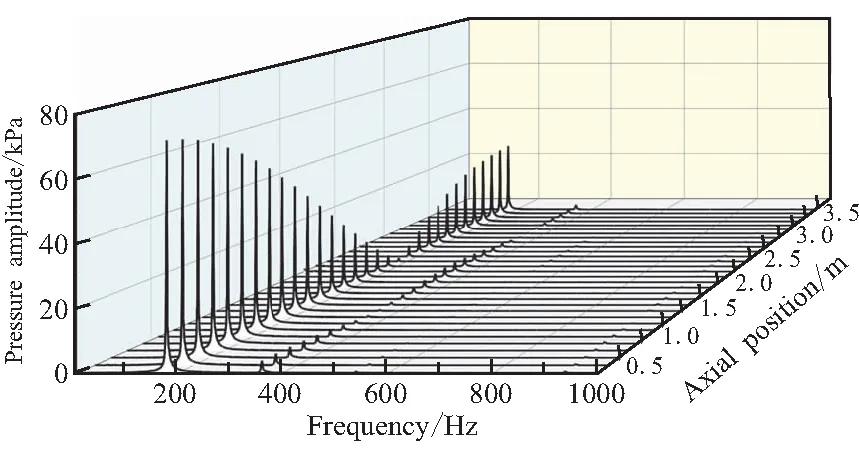
(a)Tn=0.4

由图14(c)可见,同前两个时刻的计算结果相似,燃烧室中一阶声模态下的振荡是最为强烈的,二阶声模态的振动基本已经不可见,压强振幅在轴向位置上分布同燃烧室的声模态振型相一致。此时,燃烧室一阶声模态频率为197 Hz,发动机的结构呼吸模态频率为286 Hz。Tn=0.8时刻燃烧室头部压强振幅为41 kPa,尾部压强振幅为32.9 kPa,头部测点压强振幅是尾部的128%,燃烧室头部后尾部之间压力振幅之间的差别进一步减小。尽管Tn=0.8时刻燃烧室一阶声频同结构呼吸模态频率相差相较于Tn=0.6时刻要大得多,但是压强振幅的下降程度并没有那么大。可见只要燃烧室声频同呼吸模态的频率一定距离就能够使得流场的压力振荡同结构振动相互作用引发的耦合振动加强的现象得到较大程度的缓解,从设计角度而言,只需要做有限度的结构调整就能够获得较大程度抑制效应,从而削弱燃烧室压力振荡同结构耦合振动加强的强度。

环向开槽装药燃烧室Tn=0.4、Tn=0.6、Tn=0.8时刻不同轴向位置测点的压强频谱图如图15所示。一阶声频的压力振幅最为明显,其频率为177.2 Hz,其他阶数的压力振幅在这一时刻并没有明显体现,压强振幅在轴向位置上分布同燃烧室的声模态振型相一致。

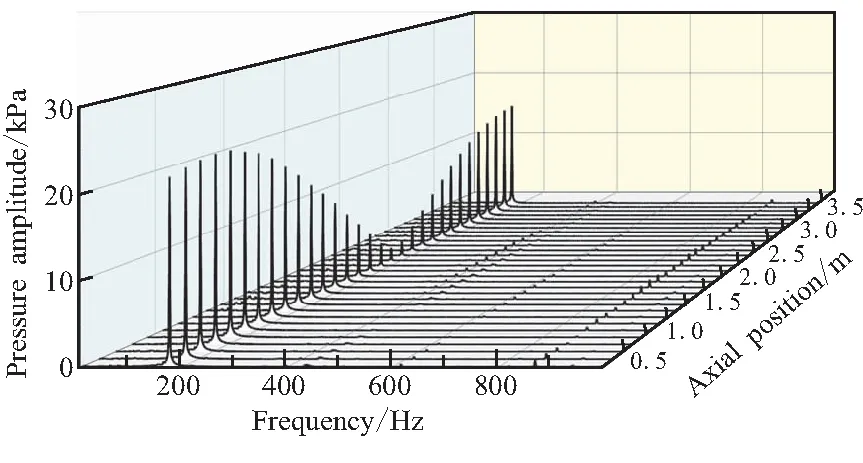
(a)Tn=0.4

由图15(a)可知,此时的发动机结构呼吸模态频率为212 Hz,同燃烧室的一阶声模态频率有较大的差距。因此,压力振荡幅值相比于Tn=0.4时刻的翼柱装药燃烧室要低得多。该时刻燃烧室头部压强振幅为21.9 kPa,尾部压强振幅为15.8 kPa,头部测点压强振幅是尾部的138.6%。

如图15(b)所示,一阶声频的压力振幅最为明显,其频率为172.2 Hz,其他阶数声频下的压力振幅在这一时刻并没有明显体现,压力振幅在轴向位置上分布同燃烧室的声模态振型相一致。

如图15(c)所示,除了一阶声频下的压力振荡,第5阶声频下的振动也表现得十分明显,这两阶压力振荡的频率分别为179.8 Hz和913.9 Hz。由此可知对于环向开槽装药燃烧室而言,在工作的后期,其部分振动能量开始向高阶声模态转移。一阶声频下的燃烧室头部压强振幅为23.3 kPa,尾部压强振幅为19.2 kPa,头部测点的压强振幅是尾部的121.4%。

为了对比两种不同装药类型的发动机在受结构脉冲加速度载荷激励作用下,燃烧室压强振荡特性,将燃烧室各时刻一阶声模态下头部和尾部测点的压强振幅进行对比,如表5所示。表中相对值为环槽型装药的压强振幅比上翼柱型装药。从表5可知,翼柱装药燃烧室的压强振幅始终要高于环向开槽型装药。尤其是头部测点的压强振幅,环向开槽装药燃烧室最低只有翼柱型的30.5%。然而,在本文计算的3个时刻,环向开槽装药燃烧室的燃面面积始终大于翼柱型,从线性声不稳定的角度看,燃面面积越大意味着燃烧室的响应增益越大,在受结构激励时能够为燃烧室的压强振荡和结构的振动提供更多的能量。由此可见,环向开槽装药发动机的稳定性要明显优于翼柱型。这主要有两个原因:第一,翼柱装药燃烧室在Tn=0.4时刻出现了呼吸模态频率同燃烧室一阶声频相接近的情况,造成了燃烧室压强振荡同结构振动之间出现了相互耦合振动加强的现象,使得两者的振动幅度得到了加强,而环向开槽型装药发动机在整个工作过程中均未出现两种振动的频率相接近的情况,从而避免了耦合振动现象的发生;第二,环向开槽型装药燃烧室的头部和尾部区域存在有环槽,这些环槽对燃烧室内的压强振荡起到了较明显的阻尼作用,从而使得翼柱装药发动机头部位置测点的压强振幅即使在呼吸模态频率同一阶声频不再那么接近的情况下仍要更大一些。而由于两种燃烧室尾部位置均存在特殊的几何结构可以对压强振荡起到阻滞作用,加之这里的流速远大于头部,流动的非定常特性更为明显。从而使得两测点的压强振幅基本相接近。由上述分析可知,对于固体火箭发动机燃烧室来说,需要避免在整个工作中结构的呼吸模态频率同燃烧室声频相接近,以及设计推进剂药型时,尽量使燃烧室的声腔中可以存在对压强振荡起阻尼作用的结构,如本文的环槽结构。同时也说明,对于这种不断有能量释放的燃烧室而言,结构对振动的吸收作用并不是主要的,即推进剂厚度对不稳定燃烧的影响并不是因为对振动的吸收能力改变而引起的,更多的是由于结构呼吸模态的变化导致与声频的接近程度产生的。

表5 燃烧室头部和尾部测点一阶声频压强振幅

3 结论

(1)本文以轴向长度相同的翼柱装药和环向开槽装药燃烧室为研究对象,使用本文构建的计算方法,研究了两种燃烧室在三个典型工作时刻受到结构脉冲加速度载荷作用下燃烧室压力振荡特性。通过对燃烧室轴向不同点的压力振幅进行分析可知,发动机结构呼吸模态频率与燃烧室的声模态频率的接近程度以及燃烧室的不同特征结构,将导致在结构激励作用下燃烧室的压强振荡特性表现出明显的差异。

(2)在结构脉冲加速度载荷的激励下,燃烧室中产生的压强振荡以一阶声频为主,发动机结构振动也表现出相似的振荡特性。可推知,当脉冲激励结束,燃烧室发生持续振荡后,激发的压力振荡带动了结构一同振动,这一点同实际中观测到的固体火箭发动机发生不稳定燃烧现象时弹体的振动特性相类似。因此,可以从避免燃烧室声频同结构呼吸模态频率相接近方向入手,抑制燃烧不稳定现象。此外,燃烧室的特殊几何结构可以对压力振荡起到明显的阻尼作用。

(3)本文中的环向开槽装药燃烧室的稳定性要明显优于翼柱装药,在受结构脉冲激励作用下产生的压力振幅要明显低于翼柱型。主要原因有两个:第一,环向开槽型装药燃烧室在整个工作过程中其呼吸模态频率一直远离燃烧室的一阶声频,而翼柱型则在Tn=0.4时刻出现了两种频率相交的情况,这就使得压强振荡和结构振动出现耦合振动,从而使振幅较大;第二,环向开槽装药的头部和尾部的环槽结构在整个工作过程中一直存在,对压力振荡起到了阻尼作用。因此,环向开槽结构替代翼柱结构,可以明显提高发动机的稳定性。