非线性燃烧不稳定振荡幅值演化特征信号辨识方法研究①
2023-04-26张翔宇金秉宁魏少娟刘佩进
甘 林,张翔宇,金秉宁*,魏少娟,刘佩进
(1.西北工业大学 燃烧、热结构与内流场重点实验室,西安 710072;2.中国航天科技集团有限公司四院四十一所,西安 710025;3.空军工程大学 装备管理与无人机工程学院,西安 710000)
0 引言
非线性燃烧不稳定问题一直是固体火箭发动机研制过程中常遇到的棘手问题之一[1-5],其典型特征是在发动机燃烧中产生非线性压强振荡现象[6-10]。通常,这种非线性压强振荡中包含一个或多个声振荡模态,且各阶模态受增益阻尼因素的影响,能量从低阶模态向高阶模态传递,激发出高阶模态,使得不稳定问题愈加严重[11-15]。然而,目前仍存在对能量传递演化机理认识不清的问题,无法对非线性燃烧不稳定的预估和抑制提供理论指导。因此,需要开展能量传递演化机理的研究,而进行这项研究的前提则是从非线性振荡数据中准确的得到各阶模态的关键参数,如振荡频率和幅值等。
对于固体火箭发动机非线性不稳定振荡数据,科研人员多采用商业软件平台进行分析,其特点是功能强大,操作简单,经过长期探索,可以形成一套数据分析流程。但在使用过程中发现,商业软件中很多模块方法和参数不明确,使得数据处理结果出现失真;此外,受主观经验判断的影响,分析结果也存在一定的误差。在处理类似信号如电力系统低频振荡信号、机械系统振动衰减信号等方面,更多的是采用时频分析方法,如经验模态分解(EMD)[16]和变分模态分解(VMD)[17-18]等,并且取得了较好的效果。综上,有必要借鉴处理类似信号的分析方法建立一种方便而准确的分析固体火箭发动机非线性燃烧不稳定振荡数据的方法,以获得非线性不稳定振荡数据的关键参数。
固体火箭发动机非线性燃烧不稳定振荡数据是典型的非线性信号。在非线性信号处理方面,典型的时频方法有经验模态分解(EMD)[19]、局部均值分解(LMD)[20]、本征时间尺度分解(ITD)[21]和变分模态分解(VMD)[22]等。其中,前三种基于递归迭代的思想,能够对信号模态进行分解。然而,EMD存在着一些问题,如缺乏严格的数学公式,易受模态混叠、端点效应、过拟合和欠采样的影响;LMD在抑制端点效应和模态混叠方面优于EMD,但其主要问题是计算复杂度高,仍容易产生模态混叠;ITD存在末端效应和时间分辨率低的问题;而VMD方法基于求解一个完全非递归变分问题的思想,具有理论上严谨的数学原理和对噪声及采样的鲁棒性等优点[23]。但VMD方法依赖于经验,需要人工预先设定模态分解个数K、二次惩罚项α和带宽τ,参数设置不当可能导致模态混叠,影响分解结果的准确性[24]。
综合考虑,本文引入了VMD[24]算法,并采用标准粒子群优化算法(SPSO 2011,以下简称SPSO)[25]对VMD算法所需的预置参数进行优化,建立了SPSO-VMD方法。将SPSO-VMD方法应用于典型特征的燃烧不稳定声振荡信号处理,准确地获得了各阶模态的频率和幅值,验证了该方法的可行性。并将其应用在了真实发动机振荡数据的处理上,准确地分离出了各阶模态。
1 SPSO-VMD方法的建立
VMD方法将原始信号X(t)分解为K(模态分解个数)个紧绕其中心频率ω的本征模态函数。在该算法中,定义本征模态函数(IMF)为一个调幅-调频信号,VMD分解过程实质上是变分问题的构造和求解过程,详见文献[24]。
SPSO算法是粒子群算法(Particle Swarm Optimization,PSO)[26]的一种改进。PSO算法作为一种群体智能优化算法,具有原理简单、易于实现和搜索速度快等优势,在PSO算法中,群体中的每个个体称为一个粒子,代表优化问题的一个潜在解。对于一个n维优化问题,每个粒子被赋予一个n维速度向量和n维位置向量。在每一次迭代也即搜索的过程中,每个粒子根据自身的搜索经验和群体中其他粒子的搜索经验动态调整各自的运动状态,从而保证每个粒子逐步向问题的最优解方向靠近[27-28]。但是,基本PSO算法存在两个缺陷:(1)不能很好地动态调整粒子的全局和局部搜索能力;(2)粒子容易陷入搜索迭代停滞[29]。RATNAWEERA等[30]为克服PSO算法的第一个缺陷,提出了线性自适应参数调整法则,即根据当前迭代次数和最大迭代次数,线性地调整参数的值;CLERC等[25]为克服基本PSO算法过早陷入迭代停滞的缺陷,提出了SPSO算法。
在SPSO算法中,首先根据每个粒子的当前位置Xi(t)、粒子的个体最优位置Pbesti(t)以及群体的全局最优位置Gbest,为每个粒子定义一个超球面;然后,在定义的超球面中,为每个粒子随机产生一个新的位置点;最后,将这个随机产生的位置视为扰动添加到粒子的速度更新公式中,所以在迭代初期,SPSO算法可从最大程度上保证每个粒子的飞行速度不为0。可以尽量保证在迭代的初期每个粒子都能以非零速度在解空间中一直搜索,从而避免算法过早陷入迭代停滞。
本文按照线性自适应参数调整法则的SPSO算法优化VMD分解,建立了SPSO-VMD方法,其思路如下:影响VMD算法的三个需要提前输入的参数为模态分解个数K、二次惩罚因子α和带宽τ。在处理的过程中,模态分解个数K是通过对振荡信号进行傅里叶变换并滤波从而确定的;二次惩罚因子α和带宽τ是通过SPSO算法来优化的。
SPSO算法优化需要一个适应度函数f(x),其定义如下:首先,对振荡信号进行傅里叶变换并滤波,得到K个模态频率及对应的K个幅值Ak;再使用VMD算法对振荡信号进行分解得到K个模态分量,对这些模态分量进行傅里叶变换,得到K个模态分量对应的K个幅值Ak,VMD(k=1,2,…,K)。各模态幅值差值ΔA计算公式为
ΔAk=|Ak-Ak,VMD|
ΔA={ΔA1,ΔA2,…,ΔAk}
(1)
将Max(ΔA)定义为SPSO算法的适应度函数f(x),也即SPSO优化VMD算法是朝着值Max(ΔA)变小的方向去优化的。
应用SPSO算法优化VMD算法流程如下:首先设定两个参数α和τ优化的具体范围,粒子在这个范围内进行全局寻优,α和τ的值由粒子的位置来表征,每个粒子每次循环将自身的位置代入VMD算法对振荡信号进行一次分解,并计算一次适应度值,通过对比新粒子的适应度值进行位置的更新,使每个粒子向着最优解方向更新位置,通过不断的迭代更新,最终找到使整个种群全局适应度最优的位置,也即所需优化参数的最佳值。
SPSO-VMD方法流程图如图1所示。
2 SPSO-VMD方法的验证
2.1 典型特征信号构建
固体火箭发动机不稳定振荡数据中包含振荡增长段、极限环段以及振荡衰减段。并且在整个振荡数据中包含多阶模态,各模态之间存在能量传递,各模态幅值变化率也随时间变化。因此,构造符合上述特征的典型的振荡信号用于校验SPSO-VMD模态分解的准确性。此时,各阶模态压强振荡幅值Rm满足的非线性微分方程[13]为
(2)
式中αm为m阶模态压强振荡的总增益系数;A为非线性系数;ωm为m阶声振模态的角频率;Emnl为表示各阶模态之间的非线性耦合作用。
按上式构造含20阶模态的仿真信号,前5阶模态的幅值以及幅值变化率如表1所示,模态数m=20。6~20阶初始幅值均为0,其幅值变化率满足αm=(m-3)×α4。在表1中,正值αm表示能量通过线性作用从燃烧场流入振荡系统中的第m阶模态,负值αm则表示能量从振荡系统中流出,高阶模态的αm的绝对值越大,表明高阶模态越难被激发以及越容易被耗散。按上式构造含20阶模态的仿真信号如图2所示。从图2可看出,上升段振荡幅值出现了明显线性向非线性转变的过程,即各阶模态的幅值并不是以线性的方式持续增长,当各阶模态能量传递达到动态平衡过程时,出现了极限环状态;下降段各阶模态的幅值变化率也是随时变化各不相同;图2(b)为整个振荡段频谱分析的前五阶结果,前三阶振荡模态的幅值占主导,所以这里仅分解前三阶模态来验证分解结果的准确性。
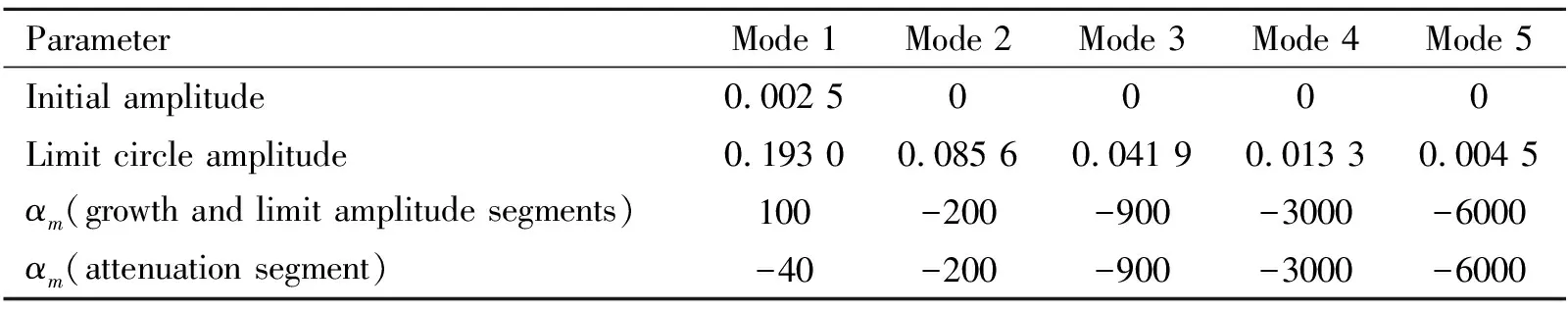
表1 前五阶模态的幅值以及幅值变化率
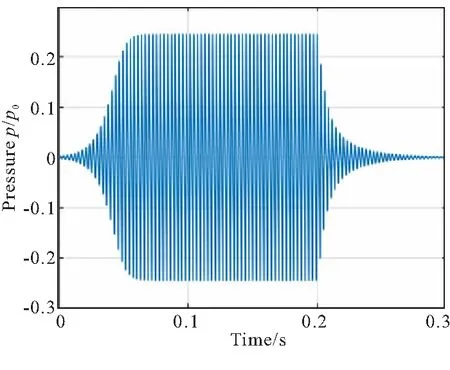
(a)Amplitude of the simulated signal
2.2 典型特征信号的SPSO-VMD方法分解
对上述信号在给定α和τ范围为(0,3000]和[0,0.2]内进行SPSO-VMD方法的分解,优化所得α和τ分别为2983.78和0.000 4。各阶模态幅值分解结果如图3(b)所示。从图3(b)可以看分解后的各阶模态幅值与图2(c)幅值轮廓线高度一致;表2展示了SPSO-VMD方法分解该特征信号的频率和幅值结果。

表2 SPSO-VMD方法分解特征信号频率、幅值结果
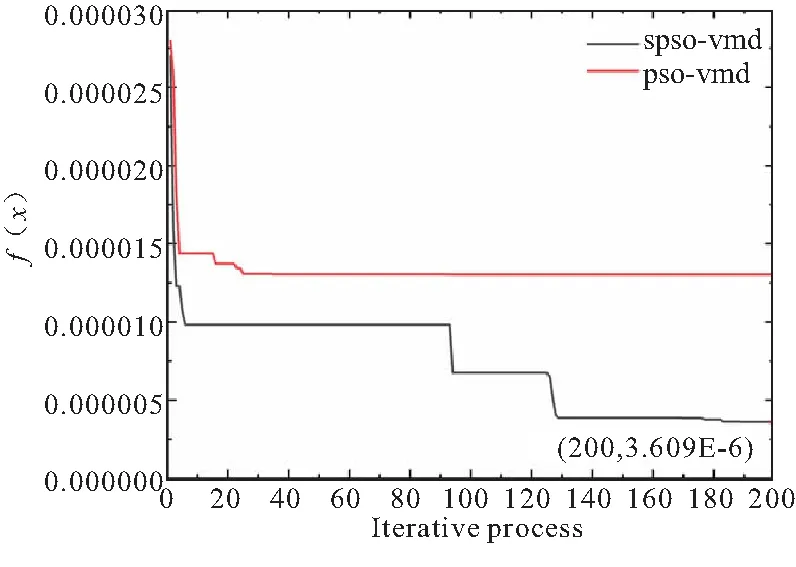
(a)Iterative process
这里三个模态的分解所得极限环幅值是通过统计的方式计算所得,其与标准极限环幅值误差均低于0.5%。从表中结果可以看出,对于非线性燃烧不稳定典型特征信号,SPSO-VMD方法能够准确的分离各个模态、辨识各阶频率和幅值。比较了以下两种方法:
(1)采用VMD算法对特征信号进行分解,分别取值α和τ为16和0.01;
(2)采用PSO算法以同样思路在同样参数范围内对特征信号进行优化VMD参数的分解,对比结果如表3和图4所示。
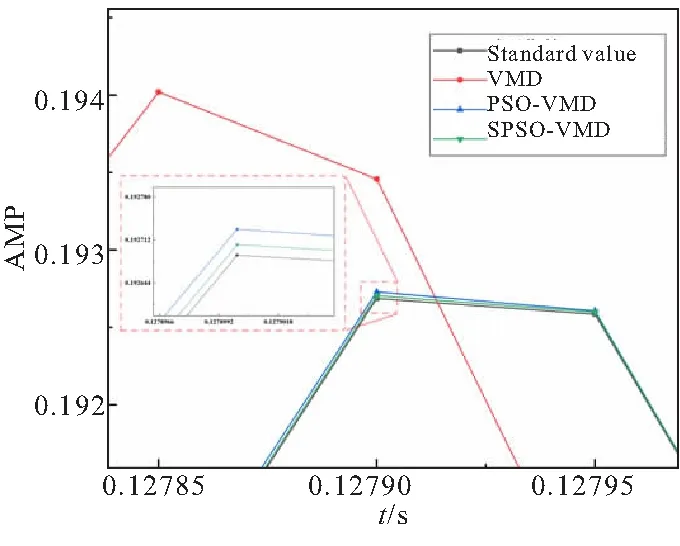
图4 Mode 1极限环段振荡某点误差示意图

表3 三种算法对比
为求出全局最小适应度函数值f(x),采用VMD法对特征信号进行分解。其中,α和τ的取值范围分别为(0,3000]和[0,0.2],α的步长为1,τ的步长为0.01,全局求解共耗时约10 h,结果如图5所示。
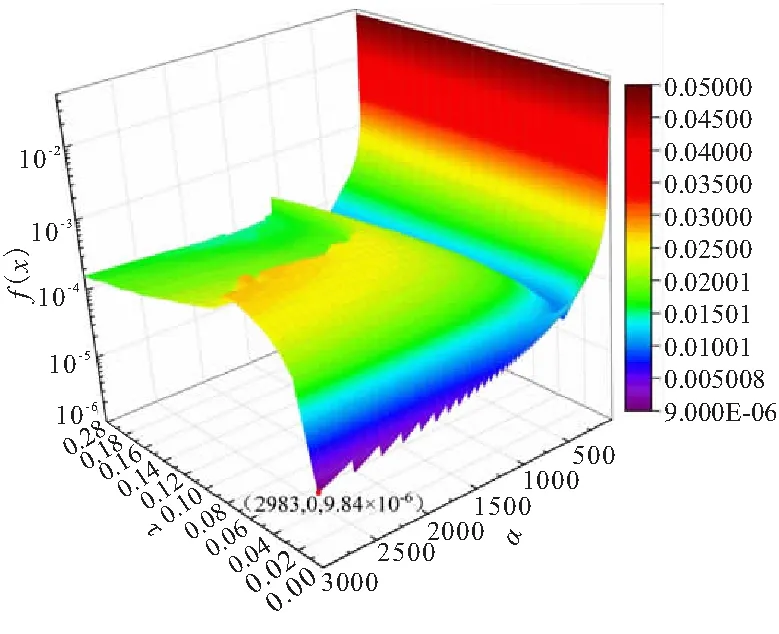
图5 f(x)的全局求解
如表3和图4所示,PSO-VMD方法和SPSO-VMD方法分解的误差远小于VMD方法。从图4中可知,SPSO-VMD方法的误差略小于PSO-VMD方法,但SPSO-VMD方法可以全局优化到与最小适应度函数值相对应的参数,且SPSO-VMD方法所需时间更短,效率更高,如图3(a)所示,在本次计算中,SPSO-VMD方法仅用3步就取得了比PSO方法更好的效果。通过两者误差的对比分析,可以认为在适应度函数为10-5数量级时,分解便已经达到了较好的效果。
3 SPSO-VMD方法的应用
某发动机在工作过程中发生了非线性燃烧不稳定,其振荡幅值数据如图6(a)所示,对其进行FFT处理。频谱结果表明,该发动机在工作过程中出现了典型的非线性燃烧不稳定现象,存在多阶模态,且前8阶模态幅值明显,通过计算分析,分解前8阶模态重构该信号的精度能达到95%,于是这里使用SPSO-VMD方法对其振荡数据进行前8阶模态分解,所用计算资源CPU型号为intel Xeon(R)Platinum 8259CL、48核,迭代在第9步时,适应度函数便达到了7.763 5×10-5,通过上一节的误差分析,可以认为该适应度值表明分解已经达到了较好的效果,对应用时约为1880 s。
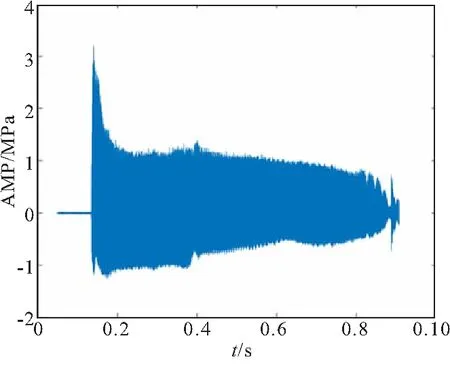
(a)Oscillation signal
8阶模态的分解结果如图7(a)~(h)所示,各分解模态的FFT结果表明,各阶模态被准确分离。
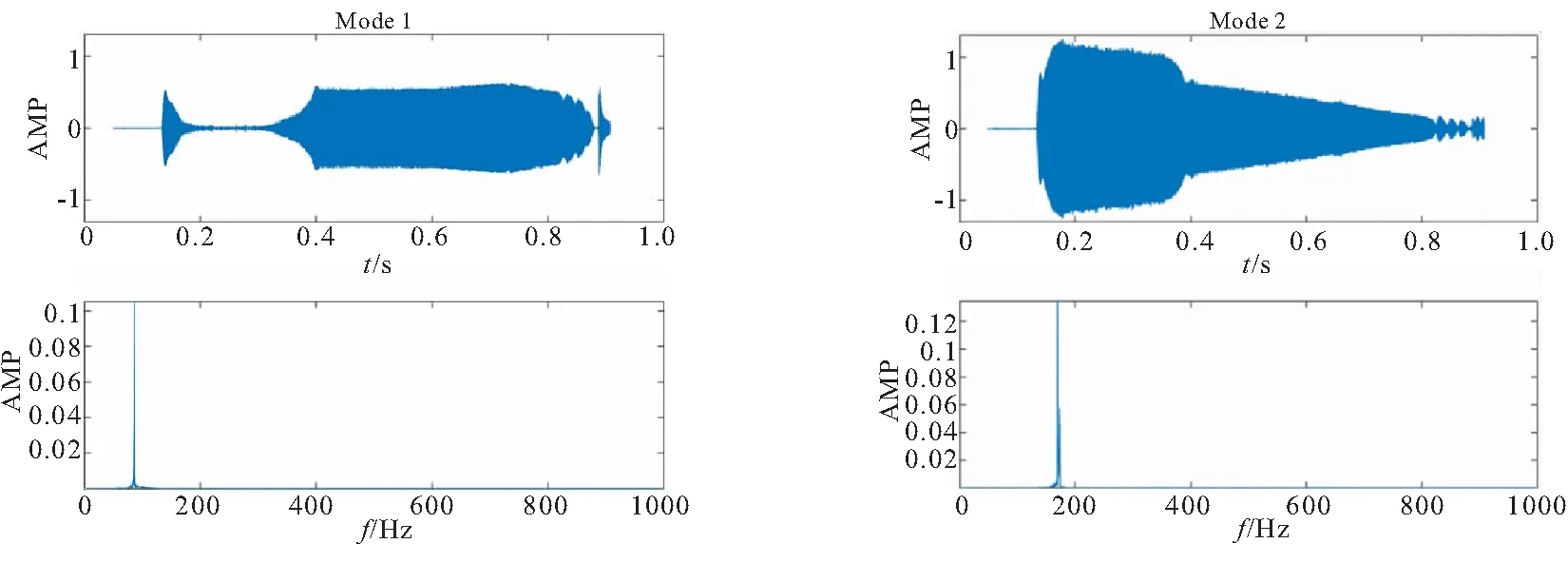
(a)Mode 1 and its FFT result (b)Mode 2 and its FFT result
针对于类似第6阶模态,频谱图上出现两个临近频率峰值的情况,这里作一定的分析:对第6阶模态进行STFT处理,所得结果如图8所示,结果表明第6阶模态在发动机发生燃烧不稳定的时间内出现了频率的变化,频谱图中两个峰值恰好对应STFT结果中振荡幅值最大的0.29 s和0.46 s两个时刻下的频率,也即这两个频率是第6阶模态不同时刻的振荡频率,它们属于一个模态。这种频率变化的现象主要是由燃烧室装药燃烧,燃面退移,导致燃烧室内声腔构型发生变化造成的。
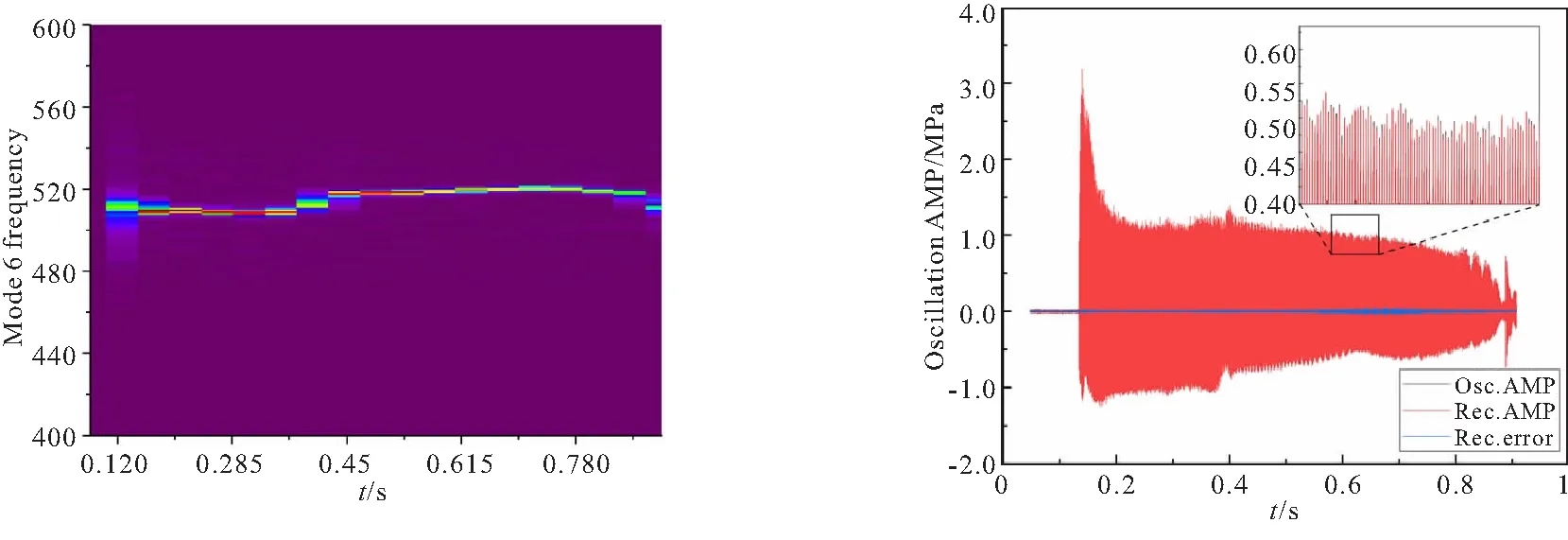
图8 第6阶模态STFT处理结果 图9 前8阶模态重构信号
这里不考虑9阶及其高阶模态,将得到的前8阶模态重新叠加,与原始的振荡幅值进行对比,如图9所示,计算前8阶模态重构振荡幅值的精度为95.2%。如图10所示,将前8阶模态绘制在同一张图中,在0.16~0.4 s时间段范围内,压强信号虽然保持极限环振荡现象,但是各阶模态的幅值却在不断变化,可看到奇数阶模态幅值衰减到了一个极小值,而偶数阶模态出现了一定的增长,仿佛出现了偶数阶增长抑制奇数阶的现象,据文献[15]所提:“非线性能量可从一阶声模态传递至所有高阶声模态,而从二阶声模态传递只能向偶数阶传递,奇数阶模态均不发生能量传递过程,且高阶声模态不能向低阶声模态传递能量。”在该发动机振荡信号中,由于某种原因,一阶模态幅值衰减到了接近0的值,传递向高阶声模态的能量极少,而二阶声模态幅值较大,不断向偶数阶模态传递着非线性能量,导致偶数阶维持一定幅值的振荡,而奇数阶高阶模态因为输入的非线性能量较少,不足以维持自身耗散的作用,导致幅值一直处在一个较低的值。这种现象恰好也提示研究人员可以从能量传递的角度对发动机非线性燃烧不稳定进行抑制,比如切断能量传输的路径或者改变能量传输的量等等,这些都有待研究。
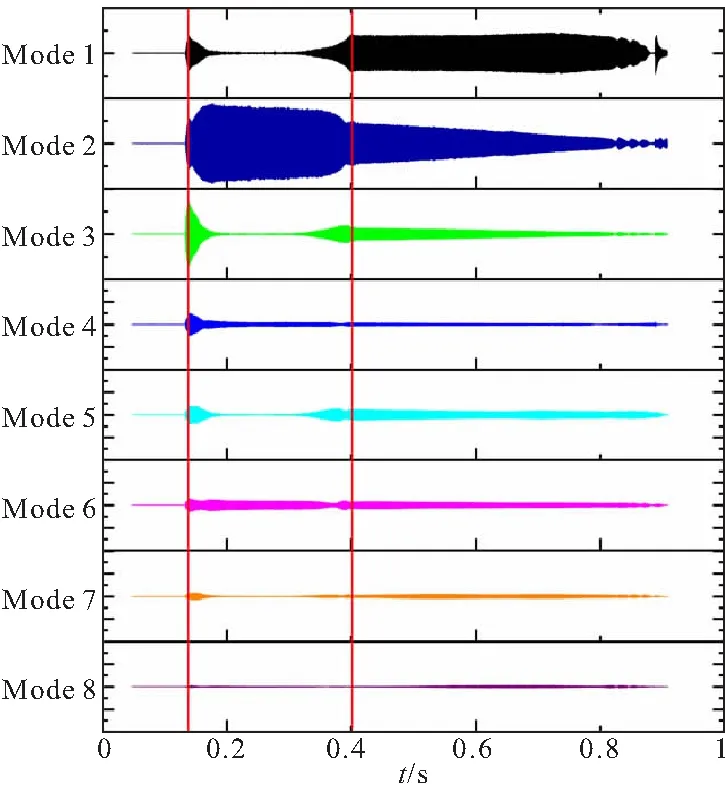
图10 前8阶模态奇偶数阶幅值演化对比
4 结论
(1)SPSO-VMD方法能够准确地分解发动机非线性燃烧不稳定典型特征信号的各阶模态,获得各模态的频率和幅值,可应用于真实发动机燃烧不稳定振荡信号的处理,可为研究非线性不稳定能量传递演化机制提供数据支撑。
(2)SPSO-VMD方法改进了PSO-VMD方法陷入局部最优解的缺陷,能够准确地找到全局最优解,分解模态误差较小,分解效率较高。
(3)SPSO-VMD方法自适应强,不依赖主观经验,集成性好,使用简单方便,可适用于工业部门对发动机燃烧不稳定问题的定位和分析。
