立体几何中的证明问题

■李富志

立体几何中的证明问题,主要就是空间位置关系的证明,这类问题包括命题真假的判断、共性(共点、共线、共面)问题,以及线线平行(垂直)、线面平行(垂直)与面面平行(垂直)问题。利用几何法来证明时,关键就是正确的空间想象与直观形象,合理的逻辑推理,综合利用相关定义、定理加以分析与证明。

一、命题真假的判断

直接利用相应的定理、定义、公理进行分析;依据题设作出简单图示,利用图示进行直观分析或说明;合理联想,将规则几何体作为模型,取其中的部分位置关系进行分析说明。

例1(多选题)中国有悠久的金石文化,印信是金石文化代表之一,印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”。半正多面体是由两种或两种以上的正多边形围成的多面体,古希腊著名数学家阿基米德研究过此类多面体的性质,故半正多面体又被称为“阿基米德多面体”。半正多面体体现了数学的对称美,如图1是一个棱数为24的半正多面体,它的所有顶点都在同一个正方体的棱上,且此正方体的棱长为1。下列关于该多面体的说法中正确的是( )。

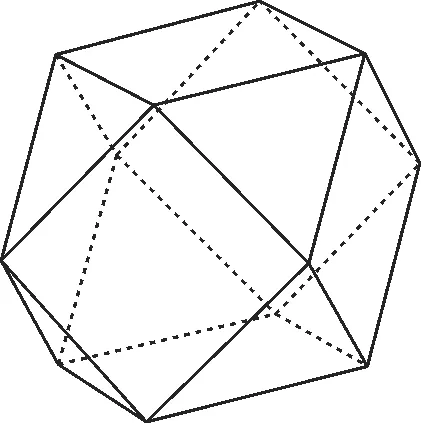
图1

A.多面体有12个顶点,14个面

B.多面体的表面积为3

C.多面体的体积为

D.多面体有外接球(即经过多面体所有顶点的球)

点评

解答这类问题,关键是利用立体几何中相关的定义、性质、定理、公理等,综合起来逐一分析,再借助空间想象与直观分析,进行合理判断。

二、共性(共点、共线、共面)问题

共性(共点、共线、共面)问题证明的关键是利用立体几何中的公理、定理与相关性质,化空间图形为平面图形进行综合分析。

例2如图2,在三棱锥A-BCD中,侧棱和底面边长均为6,H,G分别是AD,CD的中点,E,F分别是AB,BC上的点,且

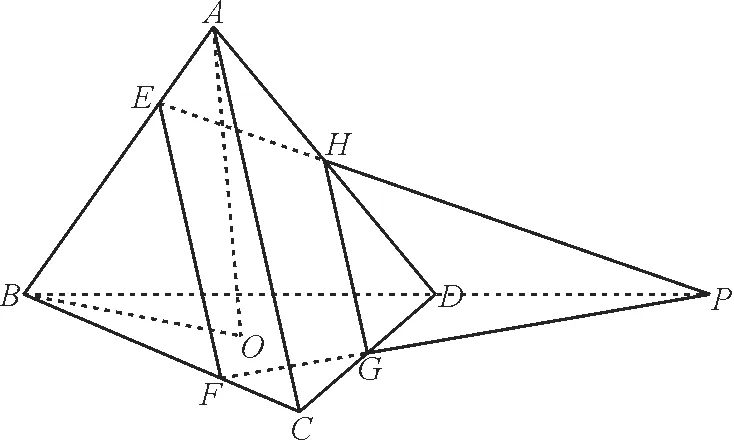
图2

(1)求证:E,F,G,H四点共面。

(2)设直线EH与FG相交于一点P,证

点评

证明空间中共性(共点、共线、共面)问题,常见的证明方法就是利用空间几何图形的结构特征,通过相关的公理、定义、性质与定理等,借助几何法的推理与论证,通过空间问题平面化进行转化与证明。

三、平行关系

平行关系证明的思路是利用空间几何体的结构特征,结合中位线定理、线面平行的性质等,构造平行四边形或寻找比例关系进行证明。

例3(2022年新高考卷)如图3,PO是三棱锥P-ABC的高,PA=PB,AB⊥AC,E为PB的中点。

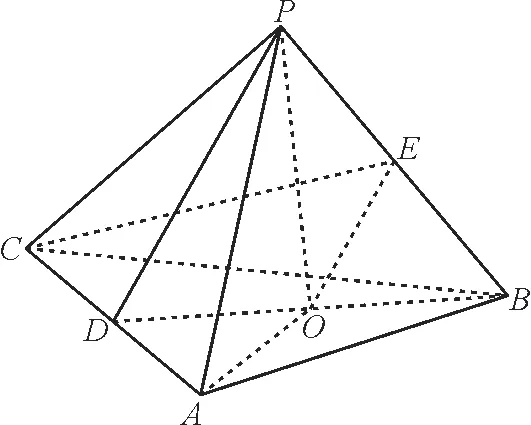
图3

求证:OE//平面PAC。

证明：依题意得OP⊥平面ABC,所以OP⊥OA,OP⊥OB,所以∠POA=∠POB=90°。因 为PA=PB,所 以△POA≌△POB,所以OA=OB。延长BO交AC于点D,连接PD。在△ABD中,因为AB⊥AC,所以O为BD的中点。

在△PBD中,O,E分别为BD,BP的中点,所以OE//PD。

而OE⊄平面PAC,PD⊂平面PAC,所以OE//平面PAC。

点评

证明线面平行时,寻找平面外的一条直线与平面内的一条直线平行,将线面平行转化为线线平行,从而进行“降维”处理。

感悟与提高

如图4,在三棱锥P-ABC中,已知△ABC是等腰直角三角形,∠ABC=90°,△PAC是直角三角形,∠PAC=90°,平面PAC⊥平面ABC。求证:平面PAB⊥平面PBC。

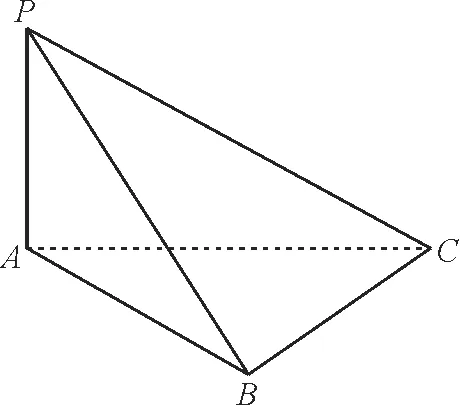
图4

提示:因为平面PAC⊥平面ABC,PA⊥AC,平面ABC∩平面PAC=AC,PA⊂平面PAC,所以PA⊥平面ABC。因为BC⊂平面ABC,所以PA⊥BC。因为AB⊥BC,AB∩PA=A,AB⊂平面PAB,PA⊂平面PAB,所以BC⊥平面PAB。又BC⊂平面PBC,所以平面PAB⊥平面PBC。