立体几何初步核心考点综合演练
2023-04-25李顺才朱亚飞欧阳亮
■李顺才 朱亚飞 欧阳亮
一、选择题
1.如图1,在△ABC中,∠ACB=90°,直线l过点A且垂直于平面ABC,动点P∈l,当点P逐渐远离点A时,则∠PCB( )。
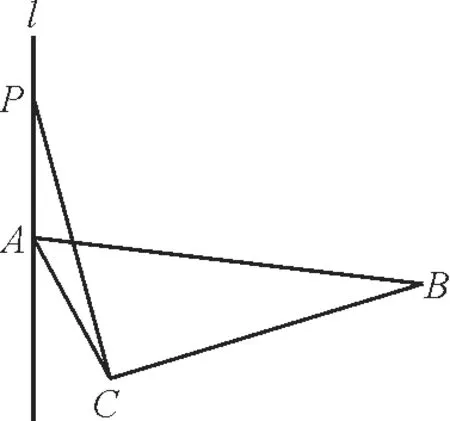
图1
A.变大 B.变小
C.不变 D.有时变大有时变小
2.球的表面积S1与它的内接正方体的表面积S2的比值是( )。

3.已知平面α,直线m,n满足m⊄α,n⊂α,则“m//n”是“m//α”的( )。
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4.在棱长为1 的正方体上,分别用过共顶点的三条棱的中点的平面截该正方体,则截去8 个三棱锥后,剩下的几何体的体积是( )。
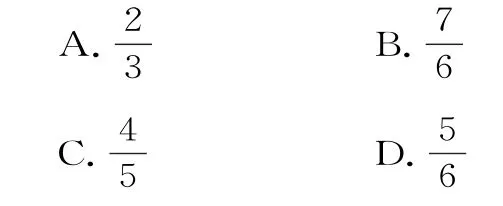
5.(多选 题)α,β是 两 个 平 面,m,n是 两条直线,下列命题正确的是( )。
A.如果m⊥n,m⊥α,n//β,那么α⊥β
B.如果m⊥α,n//α,那么m⊥n
C.如果α⊥β,m⊂α,那么m⊥β
D.如果m//n,α//β,那么m与α所成的角和n与β所成的角相等
6.(多选题)已知平面α,β,γ两两垂直,直线a,b,c满足a⊂α,b⊂β,c⊂γ,则直线a,b,c可能满足( )。
A.两两垂直 B.两两平行
C.两两相交 D.两两异面
7.(多选题)设α,β,γ为两两不重合的平面,l,m,n为两两不重合的直线,则下列命题中正确的是( )。
A.若m⊂α,n⊂α,m//β,n//β,则α//β
B.若m⊥α,n⊥β且m⊥n,则α⊥β
C.若l//α,α⊥β,则l⊥β
D.若α∩β=l,β∩γ=m,γ∩α=n,l//γ,则m//n
8.(多选题)等腰直角三角形的直角边长为1,现将该三角形绕其某一边旋转一周,则所形成的几何体的表面积不可能是( )。
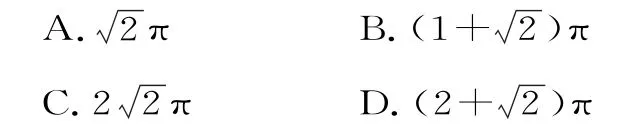
二、填空题
9.已知l,m是平面α外的两条不同直线。给出下列三个论断:①l⊥m,②m//α,③l⊥α。以其中两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题____。
10.如图2,已知矩形ABCD的边AB=a,BC=2,PA⊥平 面ABCD,PA=2,现 有以下五个数据:,④a=2,⑤a=4。
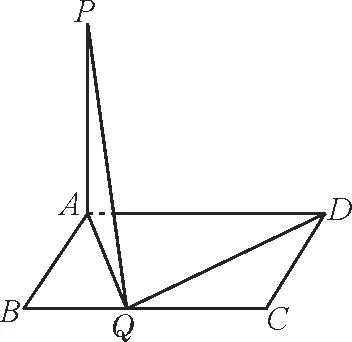
图2
当在BC边上存在点Q,使PQ⊥QD时,则a可以取____。(填上正确的数据序号即可)
11.如图3,在三棱柱ABC-A1B1C1中,点P是棱CC1上一点,记三棱柱ABC-A1B1C1与四棱锥P-ABB1A1的体积分别为V1与V2,则_____。
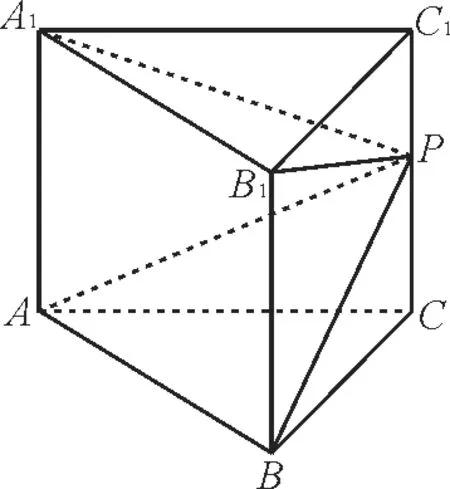
图3
12.如图4所示,等边三角形ABC的边长为4,D为BC的中点,沿AD把△ADC折叠到△ADC′处,使二面角B-AD-C′为60°,则折叠后二面角A-BC′-D的正切值为____。
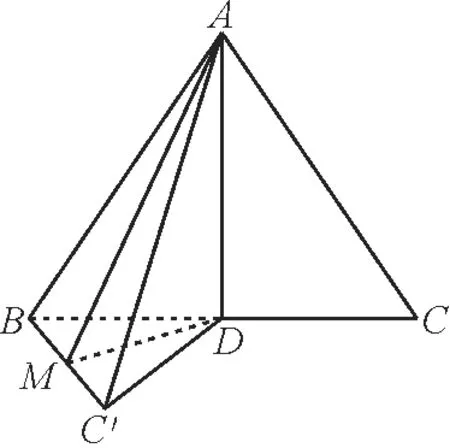
图4
13.如图5,在正方体ABCD-A1B1C1D1中,M,N分别是AB,A1B1的中点,P在AD上,若平面CMN⊥平面A1BP,则_____。
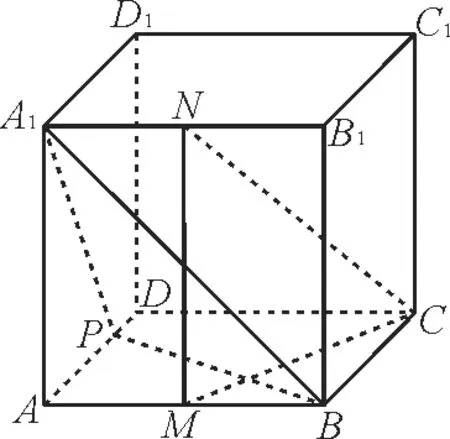
图5
14.已知过球面上三点A,B,C的截面到球心的距离等于球半径的一半,且AB=6,AC=8,BC=10,则球的半径等于____;球的表面积等于_____。
15.α,β是 两 个 不 同 的 平 面,m,n是 平 面α及β之外的两条不同直线,给出下面四个论断:①m⊥n,②α⊥β,③m⊥β,④n⊥α。以其中三个论断作为条件,余下一个论断作为结论,则你认为正确的命题有_____个,其中一个是____。
16.如图6所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,且PA= 3,AB=1,BC=2,AC= 3,则异面直线PB与CD所成的角等于____;二面角P-CD-B的大小为____。
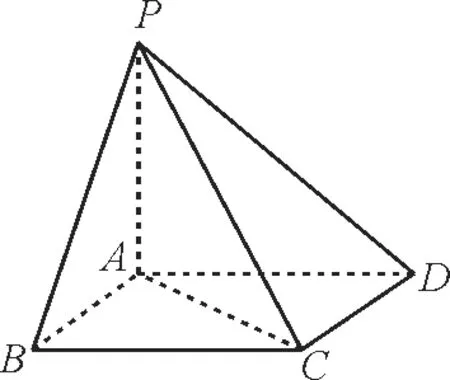
图6
三、解答题
17.如图7所示,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC//AD,∠BAD=90°,AD=3BC,O是AD上一点。

图7
(1)若CD//平面PBO,试指出点O的位置。
(2)求证:平面PAB⊥平面PCD。
18.如图8 所示,在△ABC中,CA=AB,四边形ABED是正方形,平面ABED⊥底面ABC,G,F分别是EC,BD的中点。
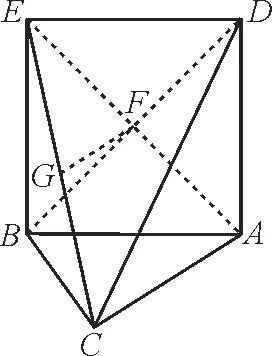
图8
(1)求证:GF//平面ABC。
(2)求证:平面DAC⊥平面EBC。
19.如图9,四棱锥P-ABCD中,底面ABCD是 边 长 为2 的 菱 形,∠BAD=,△PAD是等边三角形,F为AD的中点,PD⊥BF。
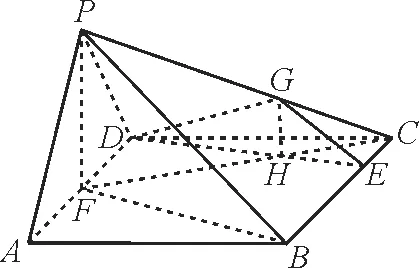
图9
(1)求证:AD⊥PB。
(2)若E在线段BC上,且EC=BC,能否在棱PC上找到一点G,使平面DEG⊥平面ABCD? 若存在,求出三棱锥D-CEG的体积;若不存在,请说明理由。
20.如图10,在四棱锥P-ABCD中,PC⊥平面ABCD,AB//CD,DC⊥AC。
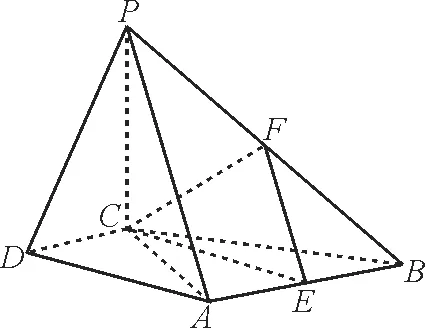
图10
(1)求证:DC⊥平面PAC。
(2)求证:平面PAB⊥平面PAC。
(3)设点E为AB的中点,在棱PB上是否存在点F,使得PA//平面CEF? 请说明理由。
21.如图11,四边形ABCD为矩形,点A,E,B,F共面,△ABE和△ABF均为等腰直角三角形,且∠BAE=∠AFB=90°。
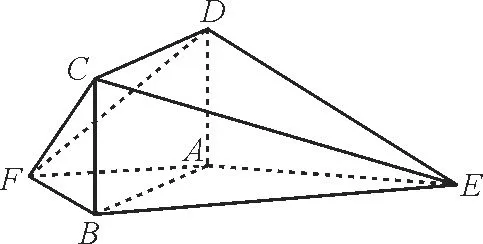
图11
(1)若平面ABCD⊥平面AEBF,证明平面BCF⊥平面ADF。
(2)在线段EC上是否存在一点G,使得BG//平面CDF? 若存在,求出此时三棱锥G-ABE与三棱锥G-ADF的体积之比。
22.如图12所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的 中 点,PA⊥底 面ABCD,PA=3。
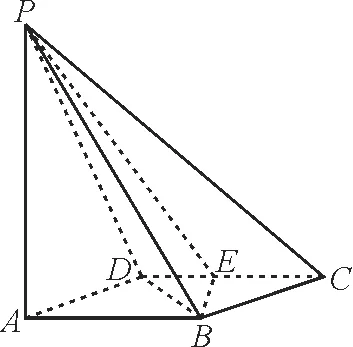
图12
(1)求证:平面PBE⊥平面PAB。
(2)求二面角A-BE-P的大小。
23.如图13,在四棱锥P-ABCD中,底面ABCD是矩形。已知AB=AD=PA=PB=2,PD=2 2。
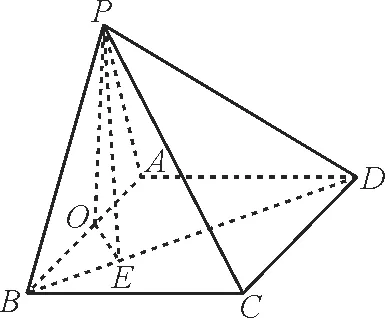
图13
(1)求点B到平面PAD的距离。
(2)取AB中点O,过点O作OE⊥BD于点E。①求证:∠PEO为二面角P-BD-A的平面角。②求∠PEO的正切值。
参考答案与提示
一、选择题
1.提示:因为直线l⊥平面ABC,所以l⊥BC。又∠ACB=90°,所以AC⊥BC,所以BC⊥平面APC,所以BC⊥PC,所以∠PCB为直角,所以∠PCB的大小与点P的位置无关。应选C。
2.提示:设球的内接正方体的棱长为a,球的半径为R,则3a2=4R2,所以。

5.提示:对于A,α,β可以平行,可以相交,也可以不垂直,A 错误。对于B,由线面平行的性质定理知存在直线l⊂α,n//l,若m⊥α,则m⊥l,所以m⊥n,B 正确。对于C,因为α⊥β,又m⊂α,所以可能m⊥β,可能m//β,也可能m与β相交,C 不正确。对于D,因为m//n,所以m与α所成的角和n与α所成的角相等。因为α//β,所以n与α所成的角和n与β所成的角相等,所以m与α所成的角和n与β所成的角相等,D 正确。应选BD。
6.提示:画出图形进行判断(图略)。a,b,c可能两两垂直;a,b,c可能两两相交;a,b,c可能两两异面。应选ACD。
7.提示:若m⊂α,n⊂α,m//β,n//β,则α与β相交或平行,A 错误。若m⊥α,n⊥β,且m⊥n,则由面面垂直的判定得α⊥β,B 正确。若l//α,α⊥β,则l与β相交、平行或l⊂β,C错误。若α∩β=l,β∩γ=m,γ∩α=n,l//γ,则由线面平行的性质定理得m//n,D 正确。应选BD。
8.提示:若绕一条直角边旋转一周,则圆锥的底面半径为1,高为1,母线长l=,这时表面积为πrl+πr2=(1+)π;若绕斜边旋转一周,旋转体为两个圆锥对底组合在一起,这时底面半径为,两个圆锥的母线长都为1,其表面积S=2πrl=π。故该几何表面积S=4πR2=。

15.提示:若①m⊥n,②α⊥β,③m⊥β成立,则n与α可能平行,可能相交,也可能n⊂α,即④n⊥α不一定成立。若①m⊥n,②α⊥β,④n⊥α成立,则m与β可能平行,可能相交,也可能m⊂β,即③m⊥β不一定成立。若①m⊥n,③m⊥β,④n⊥α成立,则②α⊥β成立。若②α⊥β,③m⊥β,④n⊥α成立,则①m⊥n成立。正确的命题有2个。若②③④为条件,则结论①成立(或若①③④为条件,则结论②成立)。
16.提示:因为底面ABCD为平行四边形,所以AB//CD,则∠PBA是异面直线PB与CD所成的角。因为PA⊥平面ABCD,所以PA⊥AB。又PA=,AB=1,所以∠PBA=60°,即异面直线PB与CD所成的角是60°。因为BC2=AB2+AC2,所以∠BAC=90°,所 以∠ACD=90°,即AC⊥CD。因为PA⊥平面ABCD,所以PA⊥CD。因为PA∩AC=A,所以CD⊥平面PAC,所以PC⊥CD,所以∠PCA是二面角P-CD-B的平面角。在直角三角形PAC中,PA=,AC=,所以∠PCA=45°,即二面角P-CD-B的大小为45°。
三、解答题
17.提示:(1)因为CD//平面PBO,CD⊂平面ABCD,且平面ABCD∩平面PBO=BO,所以BO//CD。又BC//AD,所以四边形BCDO为平行四边形,则BC=DO,而AD=3BC,所以AD=3OD,即点O是线段AD靠近点D的一个三等分点。
(2)因为侧面PAD⊥底面ABCD,平面PAD∩平 面ABCD=AD,AB⊂底 面ABCD,AB⊥AD,所 以AB⊥平 面PAD。又因为PD⊂平面PAD,所以AB⊥PD。
因为PA⊥PD,AB∩PA=A,AB,PA⊂平面PAB,所以PD⊥平面PAB。
又PD⊂平面PCD,所以平面PAB⊥平面PCD。
18.提示:(1)因为四边形ABED为正方形,所以AE∩BD=F,且F是AE的中点。因为G是EC的中点,所以GF//AC。又AC⊂平面ABC,GF⊄平面ABC,所以GF//平面ABC。
(2)因为四边形ABED为正方形,所以EB⊥AB。
因为平面ABED⊥平面ABC,平面ABED∩平 面ABC=AB,BE⊂平 面ABED,所 以BE⊥平 面ABC,所 以BE⊥AC。
易得CA2+CB2=AB2,所以AC⊥BC。因为BC∩BE=B,BC,BE⊂平面EBC,所以AC⊥平面EBC。又AC⊂平面DAC,所以平面DAC⊥平面EBC。
19.提示:(1)因为△PAD是等边三角形,所以PF⊥AD。因为底面ABCD是菱形,∠BAD=,所 以BF⊥AD。因 为PF∩BF=F,所以AD⊥平面BFP。又PB⊂平面BFP,所以AD⊥PB。
(2)能在棱PC上找到一点G,使平面DEG⊥平面ABCD。
由(1)知AD⊥BF,因为PD⊥BF,AD∩PD=D,所以BF⊥平面PAD。因为BF⊂平面ABCD,所以平面ABCD⊥平面PAD。又平面ABCD∩平面PAD=AD,且PF⊥AD,所以PF⊥平面ABCD。
连接CF交DE于点H,过H作HG//PF交PC于G,所以GH⊥平面ABCD。又GH⊂平面DEG,所以平面DEG⊥平面ABCD。

20.提示:(1)因为PC⊥平面ABCD,所以PC⊥DC。又因为DC⊥AC,AC∩PC=C,所以DC⊥平面PAC。
(2)因为AB//DC,DC⊥AC,所以AB⊥AC。因为PC⊥平面ABCD,所以PC⊥AB。因为AC∩PC=C,所以AB⊥平面PAC。又AB⊂PAB,所以平面PAB⊥平面PAC。
(3)棱PB上存在点F,使得PA//平面CEF。证明如下。
取PB中点F,连接EF,CE,CF。
因为E为AB的中点,所以EF//PA。又因为PA⊄平面CEF,EF⊂平面CEF,所以PA//平面CEF。
21.提示:(1)因为四边形ABCD为矩形,所以BC⊥AB。因为平面ABCD⊥平面AEBF,BC⊂平面ABCD,平面ABCD∩平面AEBF=AB,所以BC⊥平面AEBF。又因为AF⊂平面AEBF,所以BC⊥AF。
因为∠AFB=90°,即AF⊥BF,且BC,BF⊂平面BCF,BC∩BF=B,所以AF⊥平面BCF。
又因为AF⊂平面ADF,所以平面ADF⊥平面BCF。
(2)因为BC//AD,AD⊂平面ADF,所以BC//平面ADF。因为△ABE和△ABF均为等腰直角三角形,且∠BAE=∠AFB=90°,所以∠FAB=∠ABE=45°,所以AF//BE。因为AF⊂平面ADF,所以BE//平面ADF。又因为BC∩BE=B,所以平面BCE//平面ADF。
延长EB到点H(画法略),使得BH=AF,连接CH,HF,易证四边形ABHF是平行四边形,所以,所以四边形HFDC是平行四边形,所以CH//DF。过点B作CH的平行线,交EC于点G,即BG//CH//DF(DF⊂平面CDF),所以BG//平面CDF,即此点G为所求的点。因为BE=

22.提示:(1)由四边形ABCD是菱形,且∠BCD=60°,知△BCD是等边三角形。因为E是CD的中点,所以BE⊥CD。
因为AB//CD,所以BE⊥AB。因为PA⊥平面ABCD,BE⊂平面ABCD,所以PA⊥BE。因为PA∩AB=A,所以BE⊥平面PAB。又因为BE⊂平面PBE,所以平面PBE⊥平面PAB。
