浅淡线面平行的证明方法
2023-04-25田延兰
■田延兰
直线与平面平行是立体几何中的重要内容,也是高考的常考点。下面介绍线面平行常见的五种证明方法,供大家学习与参考。
方法一:利用几何体的性质
例1如图1,在长方体ABCD-A′B′C′D′中,下列直线与平面AD′C平行的是( )。
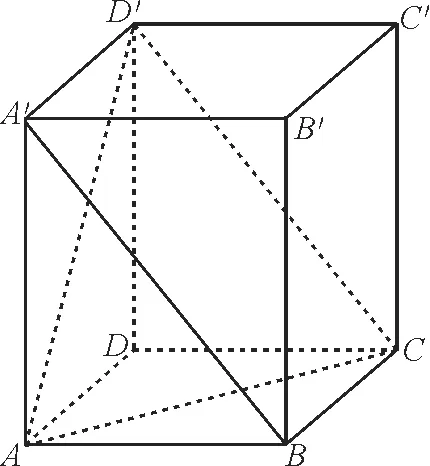
图1
A.B′C′ B.A′BC.A′B′ D.BB′
解析
因为A′B//CD′,A′B⊄平面AD′C,CD′⊂平面AD′C,所以A′B//平面AD′C。应选B。
评析:长方体相对的面(长方形)互相平行,这两个相对的长方形中对应线段平行且相等。
方法二:利用三角形的中位线
例2如图2,AB是圆O的直径,点C是圆O上异于A,B的点,P为平面ABC外一点,E,F分别是PA,PC的中点。记平面BEF与平面ABC的交线为l。
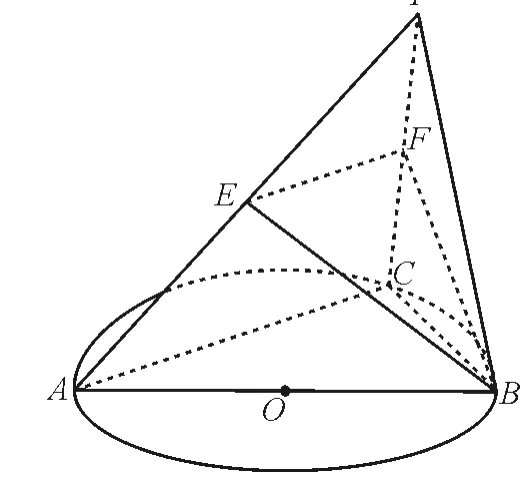
图2
求证:直线l//平面PAC。
证明:因为E,F分别是PA,PC的中点,所以EF//AC。又EF⊄平面ABC,且AC⊂平面ABC,所以EF//平面ABC。而EF⊂平面BEF,且平面BEF∩平面ABC=l,所以EF//l。因为l⊄平面PAC,EF⊂平面PAC,所以l//平面PAC。
评析:三角形的中位线平行于底边且等于底边长的一半。
方法三:构造平行四边形

例3如图3,在斜三棱柱ABC-A1B1C1中,CA=CB,D,E分别是AB,B1C的中点。PC上能否找到一点E,使得BE//平面PAD。若能,请确定点E的位置,并给出证明;若不能,请说明理由。
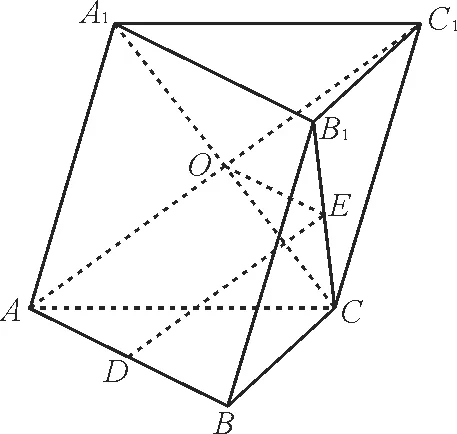
图3
解析
如图4,在PC上取点E,使,则BE//平面PAD。
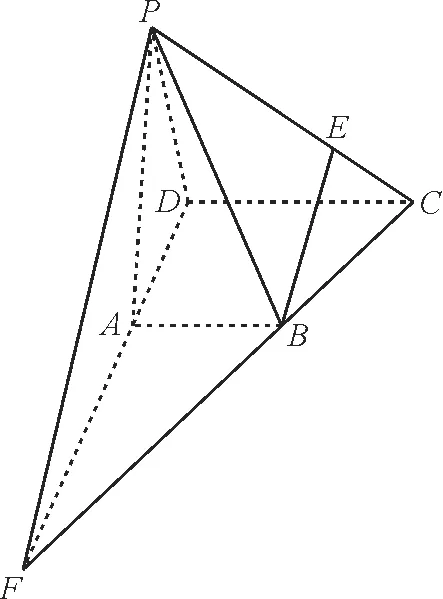
图4
证明如下。延长DA和CB交于点F。

方法五:利用平面与平面平行的性质
例5如图5,在正方体ABCD-A1B1C1D1中,侧面对角线AB1,BC1上分别有两点E,F,且B1E=C1F。求证:EF//平面ABCD。
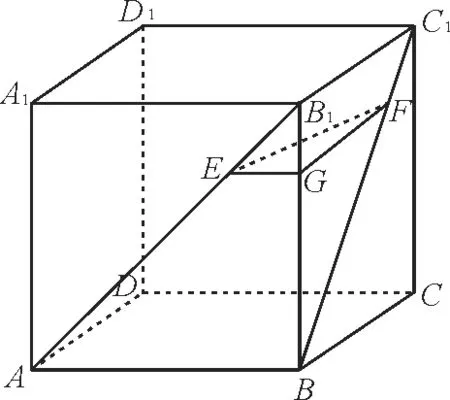
图5
证明:过E作EG//AB交BB1于点G,则
因为B1E=C1F,B1A=C1B,所以,所 以FG//B1C1//BC。易 得EG//平面ABCD,FG//平面ABCD。
因 为EG∩FG=G,EG,FG⊂平 面EFG,所以平面EFG//平面ABCD。又因为EF⊂平面EFG,所以EF//平面ABCD。
评析:线线平行,线面平行,面面平行是可以相互转化的,要特别注意线面平行关系的证明。
感悟与提高
1.如图6,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN//平面PAD,则( )。
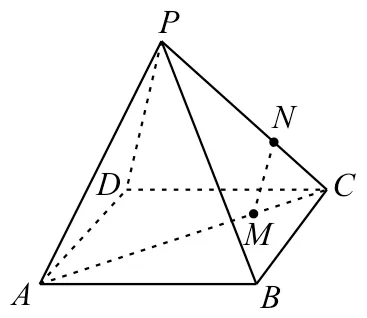
图6
A.MN//PDB.MN//PA
C.MN//ADD.以上均有可能
提示:因为MN//平面PAD,平面PAC∩平面PAD=PA,MN⊂平面PAC,所以MN//PA。应选B。
2.现有下列说法:①若直线a在平面α外,则a//α;②若直线a//b,直线b⊂α,则a//α;③若直线a//b,b⊂α,那么直线a平行于平面α内的无数条直线。
其中说法正确的个数为( )。
A.0 B.1
C.2 D.3
提示:对于①,直线a在平面α外包括两种情况,即a//α或a与α相交,所以a和α不一定平行。对于②,由直线a//b,b⊂α,只能说明a和b无公共点,但a可能在平面α内,所以a不一定平行于α。对于③,由a//b,b⊂α,可知a⊂α或a//α,这时a与平面α内的无数条直线平行。应选B。
