飞机主动侧杆的弹簧-阻尼系统力矩控制策略*

陈致君，张 诚，朱姝姝，刘 闯

(1.南京航空航天大学·南京·211106；2.中国航空工业集团公司 金城南京机电液压工程研究中心·南京·211106)

0 引 言

驾驶杆是飞机操纵系统的关键部件之一，它将飞行员与操纵系统联系在一起，主要的作用是为飞机飞行控制系统提供操纵指令。飞机操纵系统的发展历程主要有6个阶段，从机械操纵系统、助力操纵系统、全助力系统，到增稳操纵系统、控制增稳系统，再到目前应用广泛的电传操纵系统[1]。相比传统的中央驾驶杆，侧杆系统可优化座舱的显示-控制布局、改善飞机的操纵品质，且易于装配维护[2]。目前大多数飞机采用的是被动侧杆(Passive Side-Stick，PSS)，其采用弹簧加载方式，虽然结构简单、安装方便、操作稳定，但其手柄力与杆位移关系固定，无法实时调整，飞行员感受不到飞机的飞行状态[3]。

为了提高系统的操纵品质和飞行质量，主动侧杆(Active Side-Stick，ASS)成为了目前的研究热点。主动侧杆可提供力反馈功能以模拟弹簧的作用，结合飞行状态信息灵活调整杆力-位移曲线，经控制算法计算输出相应力矩，将人感与飞行状态联系起来，使飞行员获得更逼真的操纵力感觉[4-5]。

从20世纪70年代末开始，主动侧杆已在国外多种飞机上广泛应用，例如美国的F-16A/B和F-18战机、日本的T-2先进教练机、法国的幻影-2000 和阵风战斗机等[6]；除了军用飞机，美国Woodward MPC公司于 2009 年设计了应用阻抗控制的主动侧杆系统[7]，法国萨基姆公司于2014年推出了一款适用于民航飞机和直升机的新型主动侧杆原型机，2015年俄罗斯大型商用飞机 MC-21-300 上也应用了主动侧杆控制器，法国图卢兹大学和航空航天大学于 2016 年提出了基于永磁同步电机(Permanent Magnet Synchronous Machine，PMSM)的主动侧杆系统[8]。国内的主动侧杆技术研究相比国外起步较晚，目前北京航空航天大学、南京航空航天大学以及相关研究单位对主动侧杆的研究比较多，北京航空航天大学设计了一种用于飞机主动侧杆的球电机实现力反馈[9]，南京航空航天大学设计了一种采用力矩电机提供力反馈的两自由度的飞机主动侧杆系统[10]。

电动式主动侧杆杆力伺服系统以力矩电机作为力加载机构，在主动模式下，飞行员操纵手柄的动态过程需要每一个位置都能及时迅速地进行力的控制；而手柄处于稳态时，感受到的反馈力也应保持稳定，以模拟弹簧作用，因而力矩电机的转矩控制需要有较快的响应速度和较好的稳态性能。PMSM具有较高的功率密度、效率和可靠性，且随着国内外电力电子技术的发展，永磁同步力矩电机也能在大范围内实现精密的速度和位置控制[11-12]，因而采用PMSM逐渐成为主流。

本文为实现主动侧杆主动模式下的模拟弹簧的功能，将主动侧杆等效为无质量的弹簧-阻尼系统，考虑弹簧的刚度和阻尼特性得到控制参考值。对永磁同步力矩电机的电流内环采用PI控制策略，杆力误差小，动态性能好，具有良好的杆力控制性能，从而改善操纵性能，提高飞行品质。并且提出了一种主动侧杆回中定位策略，根据侧杆偏转角改变控制参考值，保证了主动侧杆自动回中的快速性和精确性。

1 主动侧杆系统结构

电动式主动侧杆在被推拉的过程中，侧杆的杆力伺服系统可根据设定的可变杆力特性曲线，给飞行员提供操纵过程中的力反馈，同时侧杆可模拟弹簧的功能，当飞行员松手后，会自动回弹到中立位。主动侧杆系统结构由三部分组成：上位机、侧杆手柄以及控制执行部分。控制执行部分主要包括控制器、电流传感器、电机驱动电路、旋转变压器和力矩电机，如图1所示。

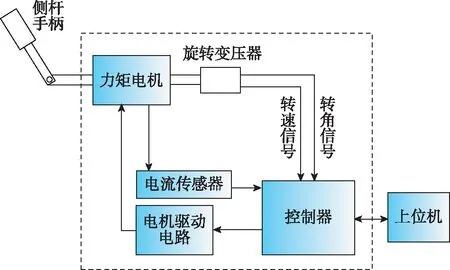
图1 主动侧杆系统结构框图Fig.1 Structure of active side-stick system

上位机使用PC机，可显示力矩电机的状态和参数，并可设定控制参数，和控制器之间进行通信。当飞行员推拉侧杆手柄运动时，控制执行部分实现杆力反馈，具体的实现过程如下：

1)旋转变压器与力矩电机的转子轴相连，侧杆带动力矩电机旋转时，旋变变压器测量电机转轴的转角和转速信号，也可根据传动机构间接得到侧杆手柄的转角信息；

2)控制器和上位机之间进行通信，接收上位机发出的指令，根据设定位移-杆力曲线得到控制参考值，接收并处理旋变变压器的转角和转速信号，电流传感器得到电机三相电流信号，通过相关的控制算法，解算出力矩电机的控制信号；

3)电机驱动电路接收控制器的电机控制信号，将其放大以驱动内部的功率电路，得到的电机三相电压信号作用于力矩电机，控制电机的输出转矩，从而实现给飞行员提供杆力反馈。

2 主动侧杆的杆力特性

主动侧杆的杆力特性曲线和侧杆的杆位移、运动状态以及飞机的飞行状态等因素有关，因此可以给飞行员提供真实的力反馈。由于本文侧重于研究力矩电机的力矩控制策略，暂不考虑飞行状态对杆力的影响，简化的杆力特性可表示为

F=Kx+Kdv+Jα

(1)

式中，F为杆力；K为侧杆的刚度系数；Kd为阻尼系数；x为侧杆转角；v为侧杆转速；α为角加速度；J为系统转动惯量。

上述三阶的杆力特性包含角加速度信息，由于实时获取角加速度的方法会增加系统成本，以及存在计算量大、精度不高等缺点，且侧杆杆力模型阶次越高越不稳定[6]，因而本文仅考虑侧杆的刚度和阻尼特性，将主动侧杆等效为一个无质量的弹簧-阻尼系统，如图2所示。

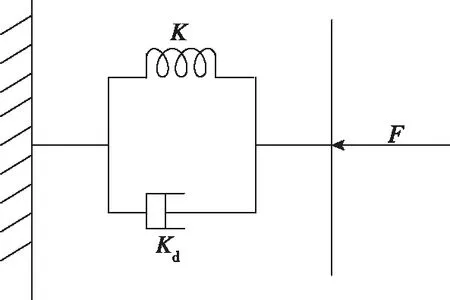
图2 弹簧-阻尼系统示意图Fig.2 Schematic diagram of spring-damping system

此时，杆力模型的表达式如下

F=Kx+Kdv

(2)

式中第一项Kx代表侧杆刚度特性，本文采用图3所示的位移-杆力特性曲线进行描述，该曲线模拟了弹簧在被拉伸压缩过程中根据不同位移反馈不同力的特性。此位移-杆力曲线为分段式线性曲线，与飞机实际受控运动相关联，图中的A点位于中立位，为主动侧杆的初始零位置，当飞行员松开侧杆手柄后，侧杆会自动回到中立位；B和C点为软止动点，当飞行员推拉侧杆超过此点位置时，感受到的反馈力会明显增大，从而给飞行员一个触觉提示，以提高操纵品质。侧杆转角和输出杆力之间的关系如式(3)所示，式中y表示杆力，x表示侧杆转角。

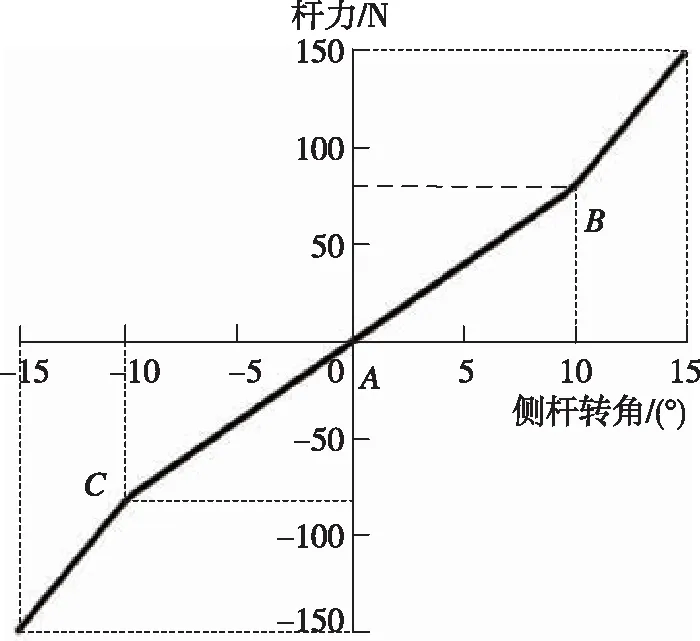
图3 位移-杆力特性曲线Fig.3 Angle-force characteristic curve

(3)

模型中第二项Kdv代表侧杆阻尼特性，阻尼是衡量物体或结构在受到外力时抵抗运动的量度，其与速度呈正比。当飞行员推拉侧杆手柄时，侧杆移动得越快，飞行员感受到的反馈力越大。当不考虑阻尼特性时，飞行员推拉侧杆到某一位置松手，侧杆回到中立位后会存在位置超调与振荡；当加入阻尼作用后，侧杆回中的过程会变得更为平缓，若阻尼系数设置得当，侧杆回中时将没有超调与振荡，可实现精确回中。

3 系统控制策略

本文针对力矩电机的电流环，采用PI控制策略，根据上述侧杆等效的弹簧-阻尼系统模型，得到电流环的控制参考量输入，从而解算出力矩电机的驱动信号，输出相应的转矩，实现主动侧杆力反馈，并加入了一种快速回中定位策略，以实现主动侧杆的快速精确回中。

3.1 PI电流环控制

基于主动侧杆的弹簧-阻尼系统模型，对力矩电机输出的转矩进行控制，通过推动主动侧杆手柄，使电机输出相应的转矩，形成杆力反馈。本文的力矩电机选用表贴式的PMSM，电机直轴电感Ld和交轴电感Lq相等，采用PI电流内环，直轴电流id=0控制，这样就可通过控制PMSM在不同转角下的交轴电流iq来控制电机电磁转矩Te的大小。PMSM的交轴电流和电磁转矩有如下关系

Te=ktiq=1.5npψriq

(4)

式中，kt为电机的转矩系数；np为电机极对数；ψr为永磁磁链。

本文采用的主动侧杆传动机构的减速比为1∶12，杆力臂为180mm，根据主动侧杆的传动结构，有侧杆杆力、侧杆转角和转速对应到电机电磁转矩、角位移和角速度，其关系表达式如下

(5)

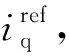
(6)

式中，Km为折合到电机端的刚度系数，和电机转角呈比例关系；Kb为折合到电机端的阻尼系数，与电机机械角速度成正比。从而可得到力矩电机电流环的交轴电流参考值。

图4 PMSM电流环控制框图Fig.4 PMSM current loop control block diagram

3.2 控制参考值的选定

根据本文采用的主动侧杆传动机构，可得力矩电机的转角-转矩特性曲线如图5所示，其表达式如下

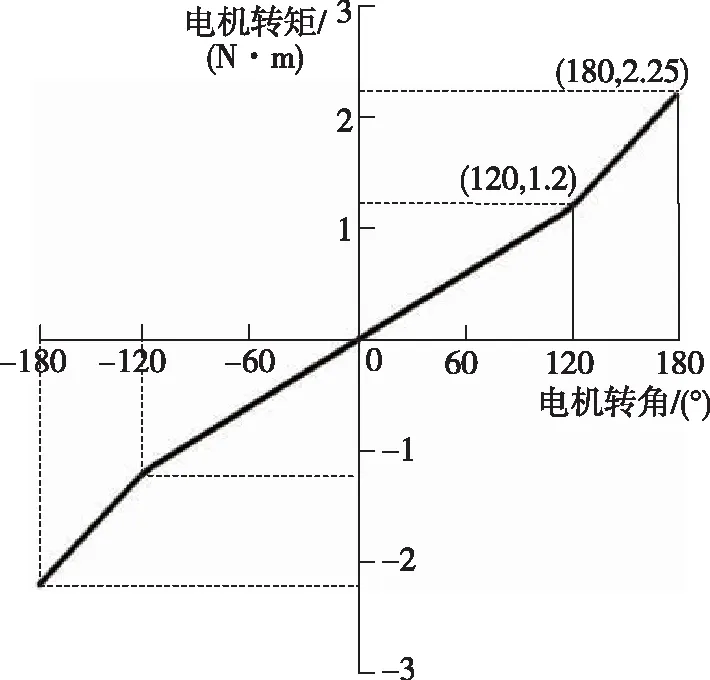
图5 电机转角-转矩特性曲线Fig.5 Motor angle-torque characteristic curve

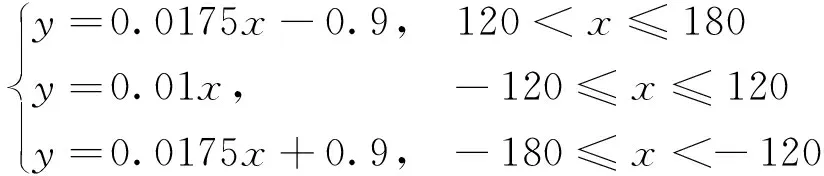
(7)

可见侧杆转角移动-15°～15°的范围对应电机转角范围为-180°～180°，侧杆杆力-150N～150N对应电机电磁转矩-2.25N·m～2.25N·m。

同时考虑到主动侧杆的运动可等效为弹簧-阻尼系统模型，因此侧杆动态运动过程具有一定的阻尼，且阻尼系数可在一定范围内调整，阻尼系数越大，阻尼作用越强。为了保证侧杆能够准确的回中，需要对阻尼系数进行分析选定。根据PMSM的机械方程有

(8)

式中，B为黏滞摩擦系数，可忽略；TL为负载转矩；Jm为折算到电机轴端的系统转动惯量，其表达式如下

(9)

式中，JL表示侧杆机械系统的转动惯量；J为电机的转动惯量。

为了使侧杆反馈力和人手推力平衡，电机的输出转矩和电机运动方向是相反的，所以将式(6)取反代入式(9)中，并进行拉氏变换，可得

Jms2θm=-Kmθm-Kbsθm-TL

(10)

将式(10)表示为电机转子机械转角θm的复变函数如下

(11)

对于本文的主动侧杆模拟平台，由动力学分析计算得到折合到电机轴端的转动惯量为Jm=6.07×10-4kg·m2；刚度系数Km根据杆力位移特性曲线折算到电机端，取0.3581；负载转矩TL取电机空载转动时的摩擦转矩，为0.25N·m。对函数进行伯德图分析，当阻尼系数取0和0.05时的伯德图分别如图6(a)和(b)所示。

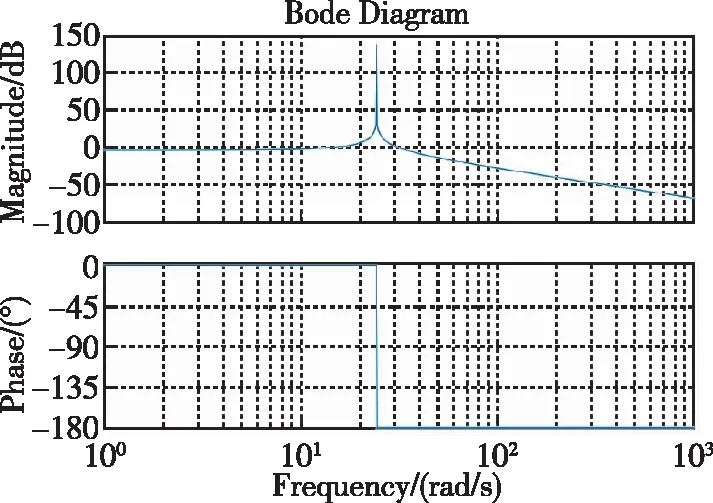
(a)阻尼系数为0时的伯德图

分析伯德图可得，当阻尼系数为0，即没有阻尼作用时，电机转角存在振荡现象，振荡频率为24.3rad/s=3.8675Hz，周期约为0.26s，而给一个合适的阻尼系数0.05后，振荡现象会被消除。

图7所示为三种阻尼系数Bm情况下侧杆从15°处自动回中的仿真图像对比，可见阻尼系数为0时，振荡周期也约为0.26s，和伯德图结果一致。而加入合适的阻尼作用后，可使侧杆回中过程变得平缓，避免主动侧杆在回中后产生位置超调和振荡，实现侧杆的自动精准回中，与理论情况相符。

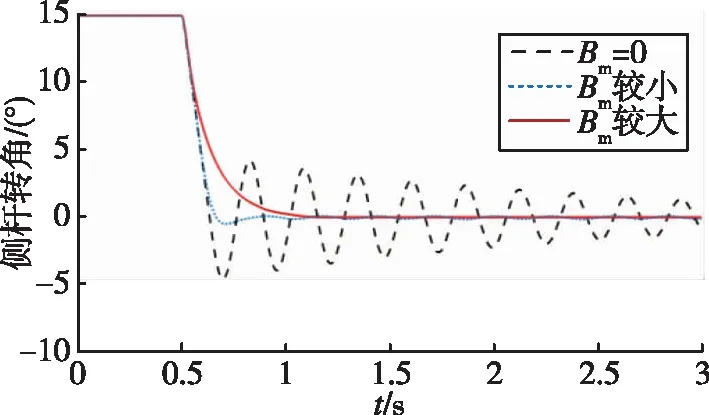
图7 不同阻尼系数下侧杆回中Fig.7 Returning to the neutral position under different damping coefficients

3.3 主动侧杆快速精确回中

在主动侧杆回中的过程中，力矩电机的转速先快速上升，当接近中立位时，转速快速下降，最终降为零。为了使主动侧杆能够快速精准回中，提出了一种回中的控制流程，当检测到飞行员松手后，根据不同的侧杆偏转角范围，改变力矩电机电流环iq参考值中的阻尼作用部分，并充分考虑回中时转速变化的特性，使回中过程的杆力变化较为平滑。回中过程中的iq参考值改为如下形式

(12)

式中，A为给定系数，用来改变阻尼作用。具体的控制流程如图8所示，其中θ1>θ2，A1<0，A2>0。

图8 快速回中控制流程图Fig.8 Flow chart of returning to the neutral position

1)侧杆开始回中时，当主动侧杆偏转角大于θ1，即偏转角在较大范围内，此时令A=A1<0，即将阻尼作用反向并乘以一个系数，这样就可以给电流环控制回路输入一个较大的iq参考值。在主动侧杆偏转角较大时，能够使力矩电机输出较大的转矩，从而加快回中的速度。且A1的绝对值越大，电机转矩越大，回中的速度越快；θ1的值越小，回中也越快；但当A1绝对值过大，或θ1的值过小会使回中产生位置超调，影响回中定位的精确性。本文侧杆转角最大行程为15°，θ1取2/3最大行程值较为合适，即10°，A1可取较大值-1.5，以使侧杆在开始回中时具有较快的回中速度。

2)当主动侧杆偏转角在θ2～θ1的较小范围内，此时令A=0，即去掉阻尼作用，减小电机的输出转矩，减缓主动侧杆回中的速度，θ2取1/3最大行程值较为合适，从而为更小角度内的精准回中作过渡。

3)当主动侧杆偏转角在0～θ2范围内，此时令A=A2>0，加入阻尼作用，进一步减小电机的输出转矩，减缓侧杆回中速度。θ2的值越小，回中越快；A2的值越小，回中也越快；但两者的值过小会产生位置超调，A2可选取一个较大值1.5，以产生一个较大的阻尼作用，保证侧杆的快速精确回中。

4 仿真实验及结果分析

4.1 仿真结果分析

为验证本文提出的主动侧杆杆力伺服控制策略的有效性，搭建了主动侧杆表贴式PMSM电流环控制仿真模型。仿真模型为离散模型，控制周期100μs，直流母线电压28V，表1所示为仿真用电机主要参数。

表1 电机主要参数

对主动侧杆手柄在-15°～15°的转角范围内进行仿真，对应电机的转角范围为-180°～180°，得到图9所示的电机转角-转矩特性曲线，图10所示为电机在0°～180°转角范围内对应的三相电流波形。可见，在电机-120°～120°的转角范围内，转矩和转角的关系基本满足y=0.01x；而在电机-180°～-120°和120°～180°的转角范围内，转矩和转角的关系基本满足y=0.0175x+0.9和y=0.0175x-0.9。这样就可以通过改变力矩电机的转角控制输出的转矩大小，从而控制反馈的杆力大小，使其符合设定的特性曲线。

图9 转角-转矩特性曲线Fig.9 Angle-torque characteristic curve

图10 0°～180°转角内三相电流波形Fig.10 Three-phase current waveform in 0°～180°

对本文的主动侧杆快速回中策略进行仿真分析，令侧杆保持在15°的转角位置，在0.5s处，侧杆在力矩电机的作用下开始回到中立位。图11所示为回中过程的转角位置响应图，其中虚线为不使用快速回中的策略，实线为使用了快速回中的策略，阻尼系数Kd都设为0.14。可见，当不采用快速回中策略时，虽然在阻尼作用下回中没有超调和振荡，但回中速度较缓慢，在约1.5s处到达中立位，耗时约1s。实线采用快速回中策略，参数设置为：θ1=10°，θ2=5°，A1=-1.5，A2=1.5，约在1.2s处到达中立位，耗时约0.7s，回中速度更快，且不存在位置超调和振荡，可实现主动侧杆的快速精确回中。

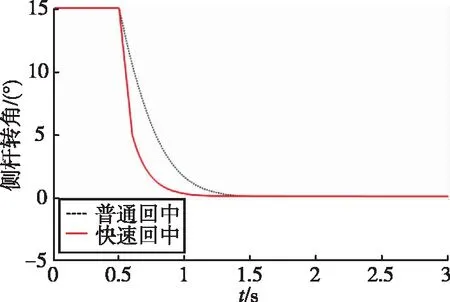
图11 快速回中对比仿真Fig.11 Contrast simulation of returning to the neutral position

4.2 实验结果分析

在一个主动侧杆模拟平台上，对本文提出的主动侧杆杆力伺服控制策略进行实验测试，并对实验结果进行分析。平台如图12所示，其中用作力矩电机的PMSM参数同仿真的电机模型参数，控制器采用快速控制原型控制器YXSPACE-SP2000，实验结果通过上位机软件获得，并使用EXCEL软件作图。

力矩电机在任意转角下都有其对应的理论转矩，并与主动侧杆的位移-杆力特性曲线相对应。对静态的侧杆转角和转矩关系进行实验测试，通过手柄转动电机到某一角度，实测转矩波形数据，8组实测转矩波动数据如表2所示。由于测试点较多，这里只给出转矩为0.5N·m和1N·m的图像，如图13所示。在0.5N·m的情况下，转矩脉动为5.589mN·m，对应的杆力波动为0.373N；在1N·m的情况下，转矩脉动为6.358mN·m，对应的杆力波动为0.424N。可见，各转角情况下的转矩符合转矩理论值，且转矩脉动都较小，对应的杆力波动也较小，从而验证了本文方法在侧杆手柄静止状态下，反馈的杆力比较精确稳定。

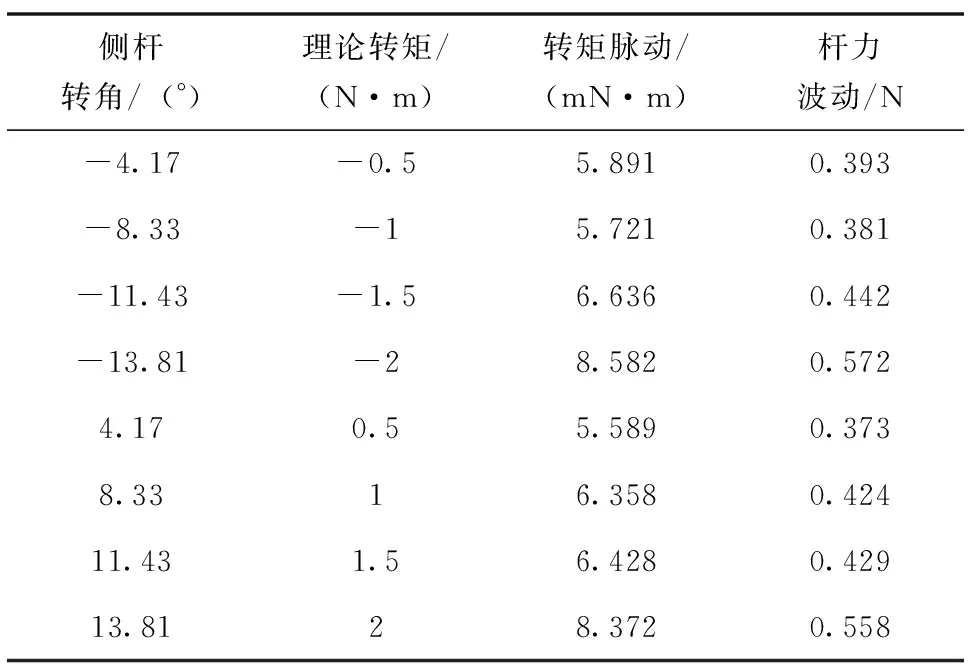
表2 多组静态转角转矩数据

通过反复推拉手柄，实测的主动侧杆位移-杆力特性曲线如图14(a)所示，其中横轴为侧杆转角，纵轴为杆力，图14(b)所示为对应的实测曲线与理论曲线的杆力误差。图15所示为侧杆正转0°～15°转角范围的动态过程中相电流与转角关系的图像，反转的图像和正转类似。可见，在侧杆手柄运动状态下，杆力的变化曲线基本符合理论的位移-杆力特性曲线，且杆力误差在±6N范围内，杆力波动较小，控制性能较好。

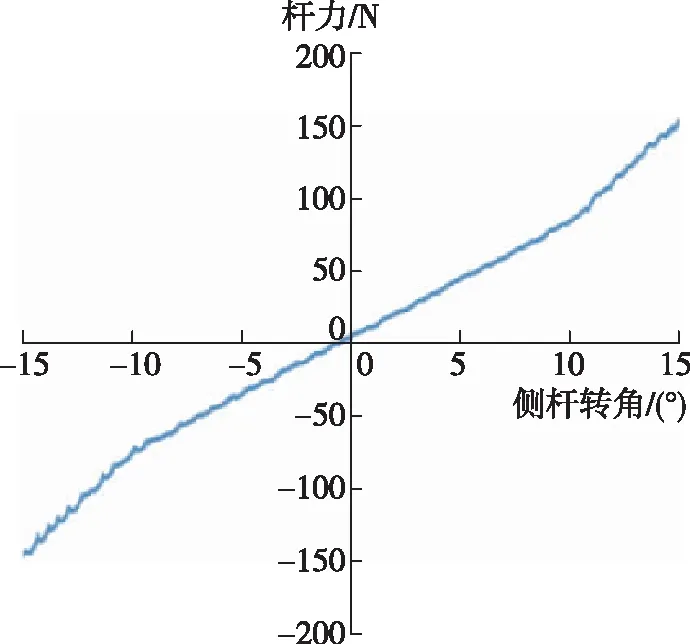
(a)动态位移-杆力特性曲线

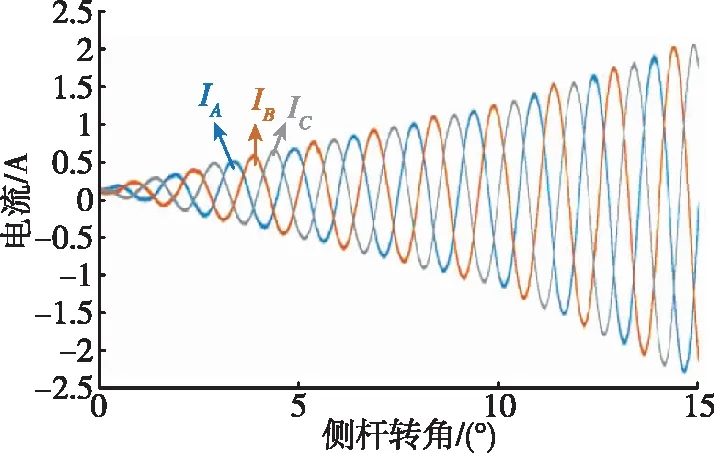
图15 相电流与侧杆转角关系波形Fig.15 Waveform of relation between phase current and stick angle

通过推拉侧杆手柄到一定角度，松手后侧杆会模拟弹簧自动回弹到中立位。将侧杆转到15°转角位置并保持，在0.5s左右处松手后，侧杆自动回中过程的实测位置波形如图16所示，其中虚线为不使用快速回中策略，实线为使用了快速回中策略，阻尼系数都设为0.15。可见，在合适的阻尼作用下，不使用快速回中策略时，侧杆在1.33s左右达到中立位，回中没有位置超调及振荡，且过程较平缓，耗时约0.83s；而采用快速回中策略时，在侧杆偏转角10°～15°范围内，系数A=A1设为-1.5，偏转角5°～10°范围内，系数A设为0，偏转角0°～5°范围内，系数A=A2设为1.7，侧杆在0.88s左右到达中立位，耗时0.38s，回中速度更快，且无超调及振荡，实现了主动侧杆的快速精确回中。

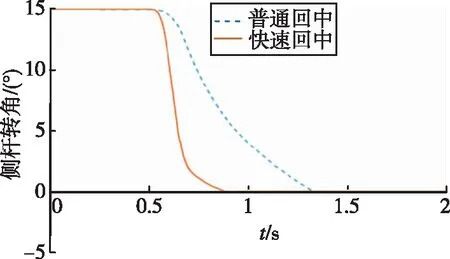
图16 侧杆快速回中对比波形Fig.16 Contrast waveform of returning to the neutral position

5 结 论

本文针对飞机主动侧杆运动控制及问题，通过模拟弹簧的特性，对主动侧杆的永磁同步力矩电机采用PI电流环控制，基于侧杆的等效弹簧-阻尼系统得到控制参考值，并采用了一种快速回中策略，在侧杆不同的偏转角范围内，改变阻尼作用。通过仿真与实验验证了此方法的有效性，结果表明此方法具有较好的转矩动静态控制性能，杆力能较好地拟合设定的位移-杆力曲线，且可实现主动侧杆的快速精确回中。