基于代理模型的卫星编队重构最短距离建模*

李 鹏，陈琪锋

(中南大学 航空航天学院·长沙·410083)

0 引 言

随着微电子技术的快速发展以及微纳小卫星技术的不断成熟，多颗小卫星组成卫星编队共同完成复杂太空探索任务已成为当今国际航天领域的一个研究热点和发展方向。卫星编队在天基合成孔径雷达、气象卫星三维立体成像和大型空间望远镜等领域有着广泛的应用前景[1-2]。

卫星编队构形重构是其区别于传统单颗卫星的重要特征和显著优势之一。构形重构是指根据不同的任务需求，使编队卫星在规定的有限时间内从初始构形转变为期望构形的机动过程，涉及轨位分配、最优路径规划、星间碰撞避免、节省燃料和燃料均衡等问题[3]。编队卫星重构机动的控制方式主要可以分为两类，一是基于冲量控制，使用双脉冲或多脉冲轨道转移策略在多种约束下实现燃料消耗最优。W.E.Wiesel[4]使用双脉冲控制完成队形重构，通过优化的方式寻找最佳的控制脉冲实施时刻。张玉锟[5]利用最优二冲量控制研究编队构形重构的底层控制问题。孟云鹤[6]提出了一种四冲量控制方法，实现了近地轨道的队形重构问题。王有亮等[7]采用遗传算法和序列二次规划结合的混合算法，研究了J2摄动下的卫星编队重构的多脉冲轨迹优化。二是基于连续推力控制，将构形重构轨迹优化问题看作一个带有状态和控制约束的最优控制问题，然后使用数值方法求解。M.Tillerson等[3]将队形重构问题简化，使用线性规划的方式优化各卫星的轨迹。G.T.Huntington等[8]使用高斯伪谱法，将卫星编队的队形重构问题转化为非线性规划问题，因其重构过程在多个轨道周期内完成，不需要考虑碰撞规避。Wu B.L.等[9]考虑了在近地轨道环境下应用勒让德伪谱法处理队形重构问题，能够处理碰撞规避及J2摄动的影响，但其计算量较大。黄海滨[10]考虑了重构过程中的碰撞避免约束，利用勒让德伪谱法将卫星重构问题转换为非线性规划问题求解。

以上的研究或者在重构过程中没有考虑碰撞避免，或者考虑了碰撞避免约束，但算法只能处理编队卫星成员数量较少(如2～3颗卫星)的情况。当卫星数量增多时，各卫星重构过程中发生碰撞的概率大大增加，此时必须考虑碰撞避免约束，需要计算编队内任意两成员星在整个重构过程中的最短距离，使其满足安全距离约束。这会带来极大的计算开销，并增加优化求解的困难。因此，有必要寻求一种能快速预测两编队卫星重构过程中最短距离的方法。

代理模型，又称为元模型或者响应面模型，可以作为解决上述问题的一种途径。所谓代理模型，是指在原模型过于复杂或者不清楚输入和输出之间的具体数学关系(黑箱函数)时，所建立的一种近似数学模型，属于机器学习领域中的回归类监督学习[11-13]。它实际上是一种“模型的模型”，无需了解设计变量与响应之间的物理意义，而是通过试验设计得到样本点的响应信息，接着利用这些信息通过插值或者拟合的方法建立数学模型，从而对未知点的响应值进行预测。代理模型经过多年的发展，已被广泛应用于机械、流体、结构和航空航天等领域。常用的代理模型技术包括多项式回归响应面(Polynomial Regression Surface，PRS)[14]、克里金(Kriging，KRG)模型[15]、径向基函数(Radial Basis Function，RBF)[16]和人工神经网络(Artificial Neural Network，ANN)[17]等。

本文以近地空间中绕参考星为中心飞行的两绕飞星为例，基于CW方程状态转移矩阵和双脉冲机动变轨方式，使2颗绕飞星在一个轨道周期内从自由绕飞状态机动到空间圆编队状态。以编队成员卫星任意的初末状态和首末脉冲施加时刻为输入，重构过程间的最短距离为输出，基于三种不同大小的训练集，分别构建了PRS、KRG、RBF、ANN代理模型，从预测精度和建模效率两方面进行对比，从而选出最佳的编队重构星间最短距离代理模型。

1 基于CW方程的重构最短距离模型

本文考虑了参考星轨道为圆轨道、绕飞星和参考星距离较近、重构时间较短且不考虑摄动的情形，因此满足使用CW方程的3个基本假设条件(圆轨道、近距离、短时间)[18]。

假设卫星初始时刻t0的状态为[r(t0)，v(t0)]T，卫星在t时刻的状态为[r(t)，v(t)]T，绕飞星相对参考星的相对运动可用CW状态转移方程来描述

(1)

根据CW方程的解析解，绕飞星以参考星为中心自由环绕飞行的初始条件为[5]

(2)

式中，x0、y0分别为初始时刻t0绕飞星相对参考星的位置矢量在参考星轨道坐标系中的径向和横向分量；n为参考星环绕地球运动的轨道角速度。

在式(2)条件下，CW方程的解析解可简化为三角函数形式

(3)

由式(3)可知，绕飞星环绕参考星的运动可分解为轨道平面内和轨道面法向的周期性运动，轨道面内的运动可由振幅b和相位角φ这2个参数决定，轨道面法向的运动则由振幅c和相位角ψ这2个参数决定。因此，可以用b、φ、c、ψ这4个参数来描述绕飞星相对参考星自由绕飞的运动状态。

绕飞星形成空间圆编队的初始条件为[5]

(4)

其中，r和θ分别表示空间圆编队的半径和相位角。

本文中编队卫星重构的过程可描述为，初始时刻伴随卫星以参考星为中心自由环绕飞行，重构开始后，通过在任意2个时刻施加速度冲量，使其在一个轨道周期后形成围绕参考星运动的空间圆编队。因此，要想得到重构过程绕飞星的运动轨迹，就需求出施加的2次冲量大小。

双脉冲变轨状态方程的冲量响应式为

(5)

式中，u=[03×1Δvi]T，Δvi表示每次机动施加的速度脉冲矢量；t1和t2分别表示施加2次脉冲的时刻。

由式(5)可知，若已知编队成员卫星的初始状态和期望状态以及2次首末脉冲的时刻，则可求出双脉冲机动重构所需的2次速度冲量为

(6)

得到2次速度冲量后，将其代入式(5)就可以求出绕飞星在整个重构过程的运动状态和轨迹。图1所示为2颗绕飞星从初始自由绕飞状态，经过2次速度冲量作用后，变轨到空间圆编队状态时，其在轨道平面和三维空间的双脉冲机动轨迹。图中圆圈表示施加速度冲量的时刻。

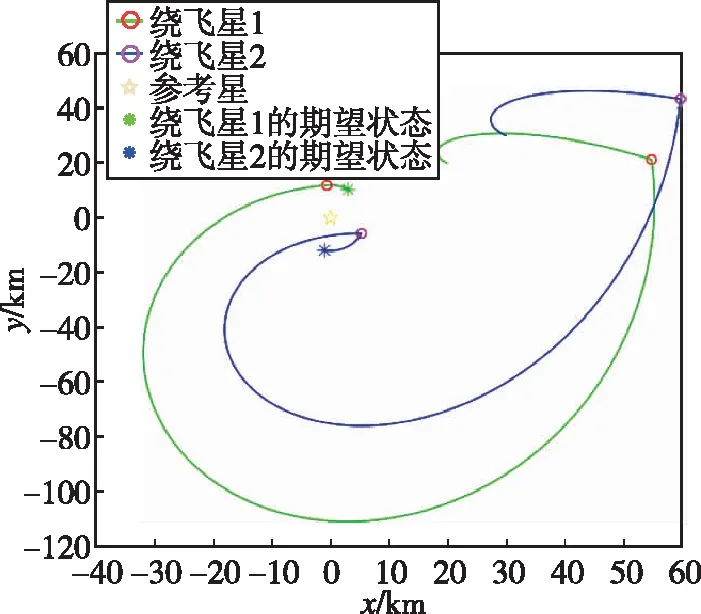
(a)轨道平面

由式(3)可知，2颗绕飞星的初始状态由b、c、φ、ψ这4个参数共同决定，期望状态由空间圆编队的半径r和相位角θ决定。两绕飞星的重构轨迹则由施加冲量时刻t11、t12、t21、t22共同决定，其中t11、t12为绕飞星1施加2次脉冲的时刻，t21、t22为绕飞星2施加2次脉冲的时刻。另外需要注意的是，本文所建立的最短距离代理模型并不针对给定初末状态的2颗编队成员卫星重构过程，而是建立在满足编队约束时任意2颗编队成员卫星重构过程之上的，即2颗成员卫星初始自由绕飞时的状态参数是任意的，期望空间圆编队中的状态参数也是完全任意的。因此，满足从自由绕飞状态重构到空间圆编队约束的任意2颗编队卫星重构过程中的最短距离dmin可表示为

(7)

式中，T表示参考星的轨道周期；下标1和2分别表示卫星编队的2颗绕飞卫星；bmin、bmax分别表示编队卫星绕飞时在轨道平面内所允许的最小和最大振幅；cmin、cmax分别表示编队卫星绕飞时在轨道面法向所允许的最小和最大振幅；rmin、rmax分别表示期望空间圆编队的最小和最大半径。

这个黑箱函数有16维输入，1维输出。在设计空间进行拉丁超立方抽样得到训练集后，经过训练即可得到重构过程最短距离的代理模型。

2 代理模型简介和模型性能指标

2.1 PRS

PRS是一种基于最小二乘法的回归分析方法，其中二次多项式响应面模型在工程和实际应用中最为常见和广泛。本文中的多项式响应面也选用二次多项式，假设输入变量与预测响应值具有如下关系[11]

(8)

式中，β为待估计的参数，可通过已知样本点信息使用最小二乘法估计得到

(9)

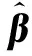
2.2 RBF

RBF是一种常用的多元散点插值预测算法。该方法通过核函数将复杂高维问题转化为简单线性问题，RBF的输入变量和预测响应具有如下关系[16]

(10)

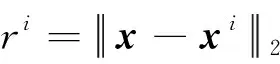
2.3 克里金法(KRG)

KRG模型是一种基于随机过程的估计方差最小的无偏估计模型，也是一种插值模型。KRG模型区别于其他模型的最大特点是，它不仅能提供未知函数预测点的响应，还能给出预估值的方差估计。KRG模型是一种插值模型，其插值结果为已知样本点函数值的线性加权。为求解加权系数，KRG模型引入统计学假设，将未知函数看成是某个高斯静态随机过程的具体实现，即未知函数在设计空间中每一点处的响应都是随机变量，服从均值为fTβ、方差均为σ2的正态分布。KRG模型的输入变量和预测响应具有如下关系[15]

(11)

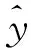
R=(R(xi,xj))ij∈Rm×m
r=[R(x1,x),R(x2,x),…,R(xm,x)]

(12)

式中，R(xi，xj)称为2个样本点的相关函数，是2个样本点欧氏距离的函数，代表不同位置处随机变量的相关性，且R的值随着距离的增加而减小，即距离为零时R=1；距离无穷大时R=0。KRG模型的性能由其基函数和相关函数共同确定。常见的基函数有常数项、一次和二次多项式。在未知函数的整体趋势未知的情况下，常数项通常被认为是一个合适的基函数选择，因此本文选用常数项作为KRG模型的基函数，此时亦称为普通KRG模型。常用的相关函数模型有高斯函数、各项同性高斯指数函数、各项异性高斯指数函数、三次样条函数和Matern函数。本文选用综合性能相对稳定的Matern函数作为KRG模型的相关函数。

2.4 ANN

ANN作为机器学习领域中最为常见的算法，由于其对非线性函数具有很强的拟合能力而得到了广泛的应用。神经网络最基本的单位是神经元，将多个神经元按照一定的规则组织在一起，就构成了最基本的ANN。最常用的神经网络为BP神经网络。BP神经网络的结构主要包括三层：输入层、隐含层和输出层[17]。有关BP神经网络的具体原理本文不再赘述，本文所采用的BP神经网络来自MATLAB中的神经网络拟合工具箱，隐含层的神经元数量设置为100。

2.5 模型性能评价指标

本文分别从模型精度和时间效率两方面来评价各代理模型的优劣。其中模型精度主要关注代理模型的全局误差准则，因此选择量纲为1的决定系数R2、相对平均误差ERA和有量纲的均方根误差ERMS[11]。R2和ERA的值均在0～1之间变化，且R2的值越高表示代理模型性能越好，其预测精度越高；相反，ERA和ERMS的值越低表示模型性能越好，其预测精度越高。

(13)

(14)

(15)

3 仿真算例

3.1 仿真条件

参考星初始时刻轨道参数：轨道高度h=622km，偏心率e=0，轨道倾角i=45°，升交点赤经Ω=30°，近地点角距ω=45°，真近点角f=60°。绕飞星的初始状态的振幅和期望状态的空间圆半径范围为：bmin=0.2km，bmax=1km，cmin=0.2km，cmax=1km，rmin=0.5km，rmax=1km。

根据式(7)，在设计空间用拉丁超立方设计方法分别抽样5000、10000、20000个样本点，组成3个不同大小的训练集，分别构建PRS、KRG、RBF、ANN代理模型。接着采用蒙特卡罗法抽样得到2000个测试点组成测试集，用于测试和验证各代理模型的精度。最后分别对比各代理模型的精度和训练集大小对代理模型性能的影响。

3.2 结果和对比

3.2.1 精度

(1)训练集大小为5000

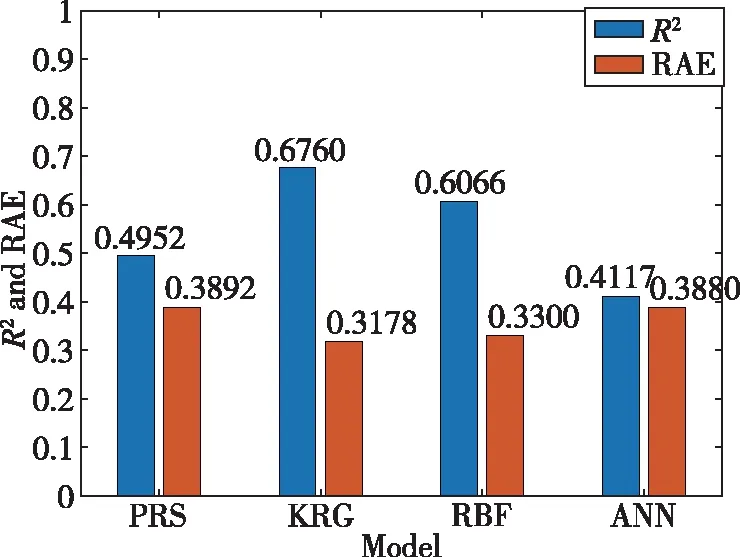
图2给出了训练集大小为5000时各代理模型的精度对比，如前所述，R2越接近1，表示模型精度越高；ERA和ERMS越小，表示模型精度越高。图2(a)显示，在训练集大小为5000时KRG模型精度最高，R2为0.6760，ERA为0.3178；RBF模型的精度稍逊于KRG模型；ANN模型的精度最差，R2仅有0.4117。原因可能是本问题的维数较高，神经网络训练得到的模型若想取得比较理想的性能，通常需要大量的训练点。此外，尽管KRG模型的精度最高，但是其模型性能仍然比较差，图2(b)显示，其ERMS为0.0968km，接近100m，难以满足实际需要。因此，需要增加训练集的样本点，以期望改善模型性能。

(2)训练集大小为10000

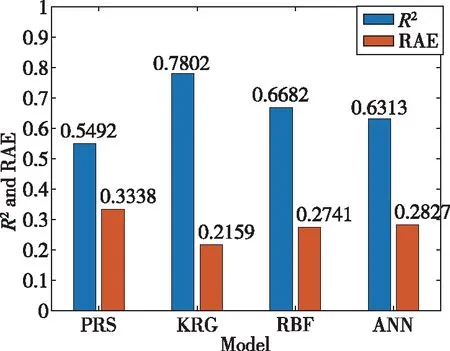
图3给出了训练集大小为10000时各代理模型的精度对比，图3(a)显示，此时KRG模型的精度仍然最高，R2为0.7802，ERA为0.2159；RBF模型的精度仍然次于KRG模型；但此时ANN的精度有所提升，R2为0.6313，ERA为0.2827，接近于RBF模型。此外，相较于训练集大小为5000时，各代理模型的精度都得到了一定程度的提升。图3(b)显示，表现最好的KRG模型的ERMS为0.0735km，比训练集大小为5000时提升了24%左右，其他模型的均方根误差也都有所下降。

(a)决定系数R2和平均相对误差ERA

(a)决定系数R2和平均相对误差ERA

(b)均方根误差ERMS图3 训练集大小为10000时各代理模型的精度Fig.3 Accuracy of each surrogate model when the training set size is 10000

(3)训练集大小为20000

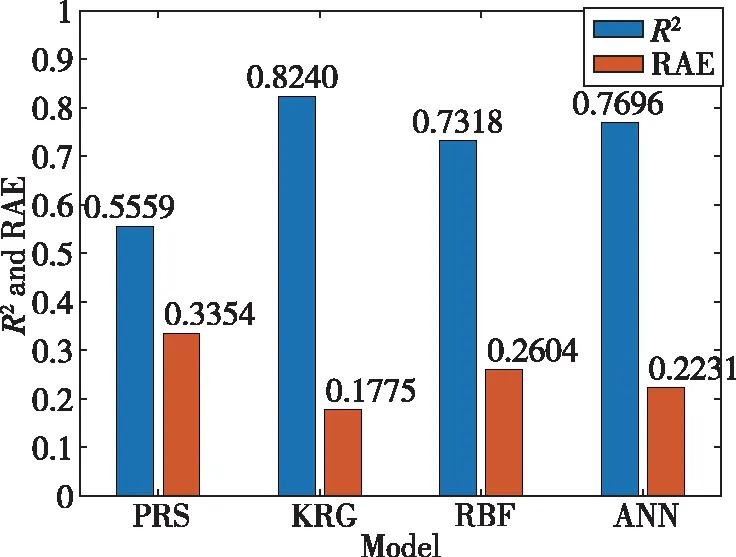
图4给出了训练集大小为20000时各代理模型的精度对比，图4显示，当训练集大小增加到20000时，PRS模型的精度并没有明显提升，其他三种模型的精度都得到了提升。其中KRG模型的精度最高，R2达到了0.8240，ERA为0.1775，降到了0.2以下，ERMS为0.0639km，比较接近60m。ANN模型的精度此时超过了RBF模型，由此可见，ANN模型对训练点的大小最为敏感，随着训练点的增加，ANN模型精度得到了较大的提升。

(a)决定系数R2和平均相对误差ERA

3.2.2 效率

代理模型的效率即为模型训练和预测未知点响应所花费的时间，时间越短，表示其效率越高。效率同时还取决于训练集的样本大小和所使用的计算平台，本文以10000个样本点的训练集和2000个测试点组成的测试集为例，统计了各代理模型训练和预测未知点消耗的时间。在一台CPU主频为2.80GHz的电脑上使用MATLAB软件进行所有的计算。表1给出了各模型训练以及预测2000个测试点所需的大概时间。

表1 训练集大小为10000时各代理模型的效率

由表1可知，PRS模型的效率是最高的，模型训练和预测的时间都少于1s。同时发现，KRG模型的训练是非常耗时的，需要花费5～6h。这主要有两方面的原因，一是因为在构建KRG代理模型时，为了获得最佳的模型精度，需要对相关函数模型中的参数(或超参数)进行优化，使得其似然函数达到最大值，本文研究的问题有16个输入变量，因此该优化问题为一个16维的优化问题；二是因为在构建KRG模型时需要求相关矩阵Rm×m的逆，m为样本点的个数，本例中为10000，因此当问题维数和样本量很大时，训练KRG模型所花费的时间较长。而对于模型的预测时间，同样发现KRG模型耗时最长，预测2000个测试点所需的时间为5～10s，这主要是因为KRG模型预测时需要计算未知点和各样本点组成的相关向量。然而需要指出的是，当时间步长为1s时，计算2000个测试点的真实输出响应耗时197s，与之相比，KRG模型预测所花费的时间仍然非常短，大大提高了计算效率。

4 结 论

本文考虑编队卫星成员数量较多时，为了生成燃料最优的无碰撞重构轨迹，需要计算任意2颗卫星重构过程的最短距离。为减少优化过程中的计算开销，本文以近地空间中绕参考星飞行的2颗卫星从初始自由绕飞状态重构机动到空间圆编队状态为例，基于CW方程和双脉冲机动变轨策略，分别构建了PRS、KRG、RBF、ANN模型，并从预测精度和建模效率两方面进行了对比。仿真结果表明，PRS模型的效率最高，但其精度较差，且随着训练集的增大，其精度并无明显提升。KRG模型的精度最高。随着训练集的增加，KRG和ANN模型的精度都得到了明显改善。KRG模型的缺点是由于问题维数较大和样本容量大导致模型训练耗时较长，且KRG模型预测未知点响应的时间同样耗时最长，但与真实模型相比，其计算耗时仍然很短，因此可以使用KRG模型作为卫星编队重构过程中星间最短距离建模的代理模型，用于后续的优化求解，以生成燃料最优的无碰撞重构规划轨迹。