运载火箭飞行振动信号盲源分离方法*

陈建宏，成 玮，陆建涛

(1. 太原卫星发射中心· 太原·030027；2.西安交通大学 机械工程学院· 西安·710049；3.南京航空航天大学 能源与动力学院· 南京·210016)

0 引 言

火箭作为太空装备的重要运载工具，一旦出现故障将造成严重的后果，轻者器箭俱毁，导致巨大的经济损失，重者甚至导致惨重人员伤亡。2011年3月4日，美国“金牛座-XL”火箭由于整流罩分离失败导致星箭俱毁，事后美国国家航空航天局(National Aeronautics and Space Administration，NASA)分析是由于火箭加速或振动造成侧轨系统不完全断开导致。2014年5月16日，携带“快车-AM4R”卫星的俄罗斯“质子-M”号运载火箭第三级发动机出现故障，导致星箭俱毁。2015年6月28日，美国“猎鹰9”火箭由于液氧罐故障发射数分钟后爆炸，执行国际空间站补给任务失败，携带的补给和设备被炸毁，造成1.1亿美元的巨额损失。据统计，运载火箭和航天器出现故障的原因超过50%来源于振动，振动问题也是火箭发动机最难解决的技术难题之一。因此，如何及时有效地提取振源信号，并对振源特征进行分析辨识，进而采取有效措施避免事故发生或减小事故损失至关重要。

火箭发动机存在振源不明、振动信号耦合、传递关系不清等问题，对火箭上采集的振动信号进行分离一直是一个难题，传统的信号分解方法，如主分量分析、奇异值分解只能得到不相关的信号，难以分离出独立的振源信息。盲源分离(Blind Source Separation，BSS)是指在源信号与信号传输先验知识很少的情况下，根据采集信号的统计特性恢复出源信号的过程。在实际中传感器采集到的往往是多个信号源成分通过不同传递路径后混叠在一起的信号，导致源信号之间频谱交叠，难以直接从混合信号中识别特征信号。独立分量分析(Independent Component Analysis，ICA)是BSS中应用最广泛的统计方法之一，是法国学者J.Herault和C.Jutten受到生物体运动时中枢神经系统能够分离不同运动信息的启发，提出的一种基于神经模拟结构的自适应算法(简称H-J算法[1])，随后又提出了ICA的概念。

国内将盲源分离用于分析机械振动信号的起步较晚，特别是针对火箭等航天航空领域振动信号的分离与识别。2004年，任海锋等[2]为了进行火箭发动机振动信号故障特征提取，运用了小波消噪技术和ICA结合的方法，对发动机热试车压强信号进行了实例分析。2005年，李舜酩[3]针对航空发动机转子故障特征分离的问题，提出了基于最小互信息的ICA方法。2008年，阳平[4]提出了结合振动信号特征信息的带参ICA方法，用于提取匹配先验知识的有用航空发动机振动信号。2009年，Ma J.C.等[5]利用ICA从航空发动机的混合振动信号中分离出源信号，并从分离信号获取特征参数，再利用隐马尔可夫进行故障判别。2010年，艾延廷等[6]针对航空发动机振动信号按照不同的激振源进行分离的问题，提出了基于最大信噪比的盲源分离方法。秦海勤等[7]为了恢复出振动信号的频域结构信息，采用了基于数学形态学滤波的源识别方法，并用于双转子航空发动机高、低压转子所激振动信号。2014年，杨凯等[8]将空间选择性去噪算法与盲源分离方法相结合，用于对航空发动机发生振动超标信号的分析，识别出发动机故障。张赟等[9]针对涡轴发动机台架试车时所测振动信号的分析问题，采用了时间延迟混合信号的欠定盲源分离方法，有效地将发动机混叠振动信号按照不同的激振源进行分离。2017年，马引刚等[10]针对液体火箭发动机故障分析与诊断问题，先利用经验模态分解(Empirical Mode Decomposition，EMD)将一维测量信号分解为具有不同尺度特征的本征模态函数，以实现对观测信号的升维，再利用ICA对各个振源信号的独立响应进行分离，以获得源信号的相关先验信息。然而，上述方法多是直接采用线性盲源分离方法进行分析，而未考虑信号在机械系统中传播产生的卷积效应。尤其是对于火箭结构而言，大尺寸薄壁壳体结构的强卷积效应不能忽略，因此，上述方法在应用到实际火箭振动信号的分析时效果不佳，难以提取到有效的振动源信号，导致振源识别困难。

针对上述问题，本文研究了一种基于卷积盲源分离的火箭振动信号自适应分解提取方法，通过构造信号的时滞模型去除卷积效应的影响，并建立火箭信号四阶统计量的代价函数，采用随机梯度法实现参数的自适应更新，迭代优化建立火箭复杂结构系统的逆滤波器结构，进而获得火箭振动源信号，并通过火箭振动数据对提出方法的有效性进行了验证。

1 运载火箭主要振源分析

火箭在飞行过程中，振动过大容易造成其携带的卫星及仪器不能正常工作、控制系统中的电路元件参数改变、紧固件松动等故障。因此，降低和控制振动噪声以改善机械系统的操作性能显得至关重要，而振动噪声源的辨识是降低和控制振动噪声的主要工作。但是火箭是一种大型复杂、激励源多样的机械系统，在很多情况下，设备之间的振动信号会互相叠加或调制。此外，各个设备运行过程及振动引起的噪声传播机理也比较复杂，造成多个激励源响应相互干扰，传递路径多样，难以建立精确模型，给火箭飞行振源的识别带来困难。火箭飞行过程主要振源如下[11]：

(1)火箭发动机稳态振动

运载火箭发动机稳定工作时，会诱发产生一种振动环境，它是由运载火箭发动机燃气产生的。这类振动通过箭体结构传递到运载火箭的各个部位，其特征也有一定的随机性。结构振动的影响不会随着运载火箭速度的增加而减少直至消失，只要发动机工作，它就一直存在。不过，通常情况下这类结构振动只对发动机附近的结构和部件产生重要影响，随着距离的增加，远处的结构和部件所受影响越来越小。例如，运载火箭的一级发动机工作时，它所产生的结构振动对运载火箭头部的卫星影响就很小。这类振动通常采用随机功率谱表示，频带范围一般为20～2000Hz。

(2)边界层脉动压力

运载火箭在大气中飞行时，其结构与大气发生相互作用，所产生的环境称为气动声环境，也称为紊流边界层脉动压力。气动噪声的形成机理比较复杂，其特征也是随机的，一般也用功率谱密度函数表述。它在运载火箭或再入航天器的外表面呈现明显的相关特性，而且周向和母线方向(飞行方向)的相关性存在较大差异。气动噪声的总均方值与结构的外形、飞行时的最大动压及马赫数有关，特别当两个部段之间的过渡肩角发生变化时，气动噪声的幅值和谱分布都将发生相应变化。当飞行马赫数超过0.85时，箭体上所产生的激波与紊流边界层脉动压力会发生相互作用，使得声压级进一步增大，甚至产生跨声速抖振载荷。气动噪声的频率范围很宽，一般上限取10kHz。

(3)跷振振动

跷振(pogo)振动在液体发动机火箭发射过程中比较突出，实质上是一种不稳定的动力学现象，由火箭结构纵向模态引起的结构振动与发动机的推力振荡相互耦合产生。结构振动使推进剂在进入燃烧室的过程中产生扰动造成推力振荡，当这种振荡与结构振动发生耦合时就诱发了跷振振动。火箭一级发动机工作时，跷振振动多发生在大型运载火箭的第一阶纵向频率附近，如5～20Hz；当二级发动机工作时，发生的频率可能超过100Hz。跷振振动的表现形式就像一种缓慢变化的极限环，在数秒至数十秒周期内，振动幅值逐渐增至最大值，然后再逐渐衰减。跷振振动的影响有时会比较严重，国外曾有跷振振动造成发动机关机的报道。

(4)储箱液体晃动力学环境

采用液体发动机的运载火箭，推进剂的质量通常占整个火箭的 90%以上；在一些大型卫星上，推进剂的质量也超过 50%。发动机工作等干扰会使得储箱内的推进剂发生晃动，而晃动所产生的载荷将体现在运载火箭或卫星的瞬态和随机振动环境中。液体晃动影响的动态频率范围一般较低，其响应幅值与推进系统的设计及所受的扰动密切相关，反过来也影响储箱本身及箭体支撑结构和连接结构的设计。

(5)火箭级间/抛罩分离冲击

火箭发射过程中，级间分离和整流罩抛罩分离一般采用火工品装置，火工品工作时将会产生高频冲击和低频瞬态环境。高频冲击对火工品附近区域的结构和设备产生较大影响，随着距离增加，这类高频冲击的影响越来越小。低频瞬态环境主要是由级间/抛罩分离过程中速度的突变引起的，这类环境在卫星设计中占据重要的地位。低频瞬态环境的特性与分离过程密切相关，但其能量谱主要集中在50Hz以下。这类低频分离环境的特点也并不完全一致，需要针对不同的分离事件逐一分析。高频冲击具有典型的瞬态特征。火工品的类型和性能有很大差异，例如，用于点解锁的爆炸螺栓、用于线解锁的柔性爆炸锁等，产生的高频冲击也有较大差异，有的集中在通过结构传递的高频冲击，有的则还包括声腔传递的部分。

2 卷积盲源分离算法

在火箭的振动信号中，传感器采集到的信号为多个振源产生的振动信号的叠加，而主要振源如涡轮泵和燃烧室等，其振动发生的机理不同，因而可认为是相对独立的，基本符合盲源分离的基本假设。在实际过程中，并不知道真实的源数目，而且火箭尺寸较大，卷积效应较为明显，因而在本研究中采用卷积盲源分离对火箭的各个信号进行估计。

2.1 卷积盲源分离模型

在具有多个振源的机械系统中，观测传感器测得的信号通常是各个振源共同作用的结果。系统的非线性比较弱时，每一条从源到观测的传递路径在时域上可以简单看作一个线性滤波器。观测信号来自于Q个源信号，通过一个线性时不变(Linear Time Invariant，LTI)多通道系统，可以表示成式(1)所示的矩阵形式

x(n)=H(n)*s(n)+n(n)

(1)

式中，x(n)为传感器测得的P维观测矢量，x(n)=[x1(n)，x2(n)，…，xP(n)]T；s(n)为Q个独立源信号，s(n)=[s1(n)，s2(n)，…，sQ(n)]T；n(n)为未知的P维噪声信号；H(n)为未知的线性混合滤波器矩阵，表示振源到传感器的传递路径。

假设H(n)为R阶的因果可逆滤波器，即因果FIR(Finite Impulse Response)滤波器。则式(1)可表示为

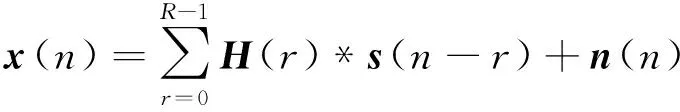
(2)

将式(2)进行z变换后，得到

x(z)=H(z)s(z)+n(z)

(3)

与瞬时混合盲源分离相似，卷积混合盲源分离的目的是仅利用观测信号x(n)与源信号分布以及统计的一些先验知识得到源信号的估计s(n)，当不考虑噪声时，即

y(n)=W(n)*x(n)

(4)

式中，W(n)为解混滤波矩阵。

对式(4)两边进行z变换，得

y(z)=W(z)x(z)

(5)

将式(3)代入式(5)，得

y(z)=W(z)[H(z)s(z)+n(z)]
=W(z)H(z)s(z)+W(z)n(z)

(6)

令

G(z)=W(z)H(z)=PΛD(z)

(7)

在无噪声的情况下(n(n)=0)，有

y(z)=G(z)s(z)
=W(z)H(z)s(z)
=PΛD(z)s(z)

(8)

其中，P是置换矩阵，导致排列顺序的不确定性；Λ=diag[a1，a2，a3，…，aQ]，是对角元素为常数的对角矩阵，导致幅度的不确定性；D(z)=diag[z-r1，z-r2，…，z-rQ]，是延时对角矩阵，导致延时的不确定性。

2.2 卷积盲分离算法基本步骤

(1)经典卷积混合模型

式(2)是对单个采样点n的经典卷积混合模型。下面考虑一种包括2N+1个采样点的块结构。

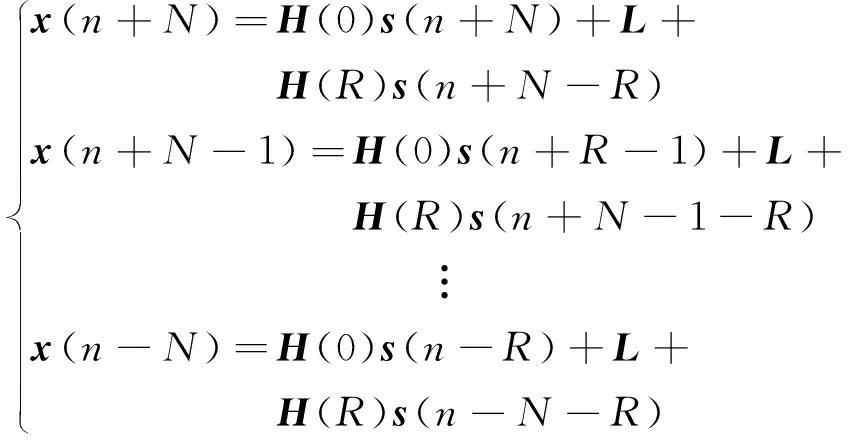
(9)

根据上述内容，就可以得到卷积混合的另一种表示形式

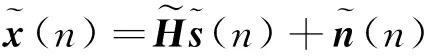
(10)

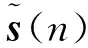
(2)利用Robust MBD抽取单个独立分量

设y(n)为需要提取的独立分量时，可以得到

(11)

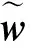
(12)

按照梯度优化方法，得到单个分量的分离矩阵更新规则如下

(13)

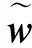
(14)

(15)

(16)

(3)各个独立分量的逐次提取

(17)

式中，Ryq是信号yq(n)的一个自相关矩阵，而ryqxp是信号yq(n)和xp(n)的互相关向量。再把yp(n)对所有混合信号的贡献cpq(n)*yp(n)从观测信号中去掉，就得到了剩下的Q-1个源的混合信号。于是就可以继续从中抽取另一个源，直到所有源信号都提取出来为止。

3 实验及结果分析

3.1 实验数据

以某液体火箭发动机飞行过程中采集数据为例进行分析。该发动机部署2个振动传感器，原始信号的采样频率为2560Hz，在1s采样时间内，2个原始观测振动信号时域波形及其频谱如图 1所示。从图1可以看出，振动信号中包含198.6Hz左右的涡轮振动、458Hz左右的燃烧频率以及一个宽频激励等三种目标信号。

图1 某液体火箭发动机振动信号及其频谱图Fig.1 Vibration signal and spectrum diagram of liquid rocket engine

3.2 基于ICA和非线性盲源分离的实验数据分析

ICA模型是最经典的盲源分离模型，其假设源之间为线性瞬时混合，以独立性最大作为优化目标实现源信号的估计。但是这是一种理想模型，在实际中较少存在，尤其是机械系统中，用ICA模型一般难以取得理想的效果。而且ICA要求传感器的数目不少于源的数目，这在某些情况下可能难以实现，而且许多时候事先并不知道源信号的数目。采用ICA对原始振动信号进行处理，得到结果为2个分离信号，其时域波形及其频谱如图 2所示。从图2可以看出，分离后信号中涡轮振动、燃烧频率和宽频激励成分仍然混合在一起，表明ICA对该信号的分离效果欠佳。

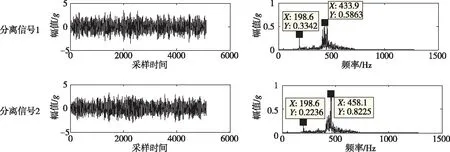
图2 ICA分离结果Fig.2 Separation results of ICA method

非线性盲源分离考虑了信号在传播过程中的非线性效应，相较于线性模型是一种更接近实际的模型。类似地，采用非线性盲源分离对原始振动信号进行处理，得到结果为2个分离信号，其时域波形及其频谱如图 3所示。可以检验分离的各个信号已具有一定的独立性，各个信号之间的相关系数较小。然而，非线性盲源分离仍然要求传感器的数目不少于源信号的数目。从其频谱可以看出，即使采用非线性盲源分离方法，仍未很好地实现源信号的分离，各个振动源信号的特征频率仍旧相互混合。

图3 非线性盲源分离结果Fig.3 Separation results of nonlinear adaptive blind source separation method

3.3 基于卷积盲源分离的实验分析

卷积盲源分离则考虑了信号在机械系统中传播时产生的卷积效应，对机械系统能够较好地近似，因而常被应用于机械信号的处理中。本文研究的卷积盲源分离方法可以通过信号的逐个抽取技术，实现欠定情况下的源信号估计，因此该方法能够在欠定情况下对机械系统源信号进行较好的估计。采用卷积盲源分离对原始振动信号进行处理，得到结果为5个分离信号，其时域波形及其频谱如图 4所示。

从图4可以明显得到198.6Hz左右的涡轮振动(对应分离信号4)、458.1Hz左右的燃烧频率(对应分离信号1)以及一些宽频激励，其中分离信号2中还可清楚发现涡轮转动的基频成分49.71Hz。从以上结果可以看出，主要信号频率分离方面，相较于ICA和非线性盲源分离方法，本文提出的卷积盲源分离方法对火箭发动机信号的分离结果更好，成功地分离出了涡轮转动主频与基频、燃烧频率和宽频激励频率。时域信号响应有效分离方面，198.6Hz的涡轮振动、458Hz的燃烧振动及宽频激励三种目标信号分离后，峰值分别达到5.004g、4.194g和0.793g，涡轮转动的基频49.71Hz分离后峰值为0.8012g，分离后时域信号能量聚焦，分离效果显著。此外，本文研究方法降低了对传感器数目的限制，能够在2个传感器信号的前提下分离出多个信号，这增加了其在实际工程中的适用性。

4 结 论

针对振动信号在火箭复杂结构中传播存在明显卷积效应的问题，本文研究了适用于火箭振动信号分离的卷积盲源分离方法。基于火箭振动源之间的独立性，优化建立火箭振动信号在火箭复杂结构传播过程中的逆系统，进而实现火箭主要振动源的有效提取。采用火箭的实测数据对研究方法的性能进行验证，结果表明，本文方法能够实现对主要振动源的有效分离。