基于深度强化学习的高超声速飞行器动态面控制方法*
2023-04-25赵琛钰朱东方
胥 彪,赵琛钰,李 爽,朱东方
(1.南京航空航天大学 航天学院·南京·211106;2.南京航空航天大学 空间光电探测与感知工业和信息化部重点实验室·南京·211106;3.上海航天控制技术研究所·上海·201109)
0 引 言
高超声速飞行器因具有机动能力强、飞行距离远、生存能力强等多重特点,在空间竞争中的重要性愈发凸显。在飞行任务需求不断提高的背景下,飞行环境日益复杂,且高超声速飞行器自身所具有的强非线性、复杂耦合效应、快速时变特性和较大的不确定性等[1],都对控制系统的设计提出了更高的要求。
目前,已有大量文献根据反步控制、自适应控制、鲁棒控制和模糊控制等多种控制理论,提出了高超声速飞行器控制方法。例如,Sun H.等[2]基于干扰观测器的反步控制方法,提出了在虚拟控制律中引入扰动估计以补偿不匹配扰动的策略,设计了不牺牲标称控制性能的自抗扰控制器。Hu X.等[3]针对高超声速飞行器的参数不确定性和未建模动态,利用模糊逻辑系统(Fuzzy Logical System,FLS)对系统进行辨识,并设计了一种具有较高效率的自适应模糊控制器。Shou Y.等[4]针对系统动力学不确定性,利用在线数据神经网络学习和扰动观测器构造了预设时间的Terminal滑模控制器,实现了系统在定义时间内收敛的效果。Bu X.等[5]针对传统预设性能控制设计中需要预先知道初始跟踪误差的限制,提出了一种性能函数以实现不需要精确初始跟踪误差的更加简洁的控制结构和更低计算负担的控制方法。反步控制凭借其固有的处理系统非线性的能力和闭环系统的自然稳定性而受到广泛关注,但是由于在设计中存在“项爆炸”的问题,使得控制器在设计时的计算十分复杂。D.Swaroop等[6]通过在非线性系统中引入一阶滤波器代替求导工作,可以克服反步设计时的计算复杂问题,并保证了系统跟踪误差的有界性。然而,在传统控制方法中,控制律通常需要设定固定的结构和参数,而一些自适应方法又需要设计复杂的自适应律,从而加深了控制器的设计难度。
随着高超声速飞行器的快速发展,对控制系统的智能化要求也不断提高,这就需要对控制系统各个关键环节进行智能化的升级改造,使得飞行器具有智能学习能力[7-9]。将深度学习的感知能力和强化学习的决策能力相结合的深度强化学习(Deep Reinforcement Learning,DRL)是一种通过感知环境变化,以深度神经网络构建智能体与环境进行交互,并以最大化奖励为目标训练智能体得到最优策略的方法。传统控制方法与先进的人工智能的关系不是简单的替代关系,而是应该探索一种结合两者优点的智能控制方法。文献[10]通过估计值函数,采用基于策略迭代的单网络积分型强化学习算法,解决了传统HJB方程难以求解的问题,设计了收敛速度更快的再入飞行器的自适应最优控制器。
由T.P. Lillicrap于2016年提出的深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)算法[11],是深度强化学习中最具代表性的算法之一。确定性策略梯度(Deterministic Policy Gradient,DPG)算法虽然可以处理连续动作空间的任务,但是无法从高维输入中学习策略[12]。而深度Q网络(Deep Q-Network,DQN)虽然可以直接进行端到端的学习,却无法处理离散动作空间的问题[13]。DDPG在DPG的基础上引入DQN算法的成功经验,实现了对高维连续动作空间强化学习问题的求解。文献[14]就利用DDPG算法,以多数据帧的状态信息作为智能体的观察状态,舵偏角和发动机推力指令作为智能体的输出动作,再经过训练后得到了具有泛化性和鲁棒性的智能飞行控制器。文献[15]将DDPG和反步法结合,在考虑执行器约束的情况下使控制律中的参数调整得到有效解决。文献[16]将自抗扰控制算法和强化学习结合,提出了高超声速飞行器巡航段的智能控制方法。文献[17]基于深度强化学习理论,设计了导弹拦截问题的制导控制一体化算法。通过强化学习算法,使得导弹可以低能耗快速稳定地拦截目标。文献[18]在速度子系统设计中采用强化学习算法,设计了基于神经网络自适应的PID参数智能调整方案。
本文设计了一种用于高超声速飞行器的姿态跟踪智能控制算法,目的是在考虑控制约束和性能最优的情况下实现姿态跟踪控制。其核心思想是建立在传统动态面控制方法基础上,使用DRL完成对控制器参数的智能优化,并且在DRL自身训练过程中达到性能最优的要求。当系统存在不确定性的情况下,智能控制算法仍能完成姿态控制。通过引入DRL算法,实现了在考虑控制量消耗和性能最优情况下的控制器参数智能优化。
1 高超声速飞行器数学模型
考虑发动机关机状态下,高超声速飞行器纵向非线性模型可以表示为如下形式[19]
(1)
式中,弹道倾角γ、攻角α和俯仰角速率ω是描述飞行器纵向姿态运动的3个状态变量;V、m和r分别代表了飞行器目前飞行速度、质量和距地心的径向距离;μ为重力常数;I为转动惯量;Δ表示系统不确定项。飞行器的升力L和俯仰力矩M表达式如下
(2)
式中,ρ为空气密度;S为参考面积;c为平均气动弦长。升力系数CL和俯仰力矩系数CM的表达式为
(3)


表1 高超声速飞行器纵向非线性模型参数表
结合实际情况,考虑升降舵偏转角的幅值约束
-30°≤δ≤30°
(4)
在设计高超声速飞行器控制律时,动态面控制方法的参数会直接影响控制效果。而传统方法中,设计参数是依靠人工经验调试的。本文采用动态面控制设计了控制器结构,将控制系数作为待定量,然后采用强化学习方法进行智能参数优化。
2 控制器设计
首先,利用动态面控制方法[6]分别设计攻角虚拟控制律、俯仰角速率虚拟控制律和升降舵偏转角控制律。然后,将问题转化到强化学习环境中,转为寻找一个最优策略函数实现跟踪性能和控制量最优。通过将强化学习算法与动态面控制方法结合,完成控制器参数智能优化。
2.1 动态面控制器设计
2.1.1 攻角虚拟控制律设计
首先,定义弹道倾角跟踪误差S1为
S1=γ-γd
(5)
令
(6)
对式(6)求导可得
(7)
(8)
其中,k1>0为控制增益。

(9)


(10)
(11)
2.1.2 俯仰角速率虚拟控制律设计
对攻角跟踪误差S2求导得
(12)
此时,设计虚拟控制律为
(13)
其中,k2>0为控制增益。

(14)
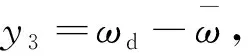

=S3+e3-k2S2
(15)
(16)
2.1.3 升降舵偏转角控制律设计
令
(17)
(18)
对俯仰角速率跟踪误差S3求导得
(19)
此时,设计最终的控制律为
(20)
其中,k3>0为控制增益;ρ3>|Δ|是阻尼项系数;ε为任意小的正实数。
(21)
对于Lyapunov函数V=V1+V2+V3,求导得

=a1S1S2+a1S1e2+S2S3+S2e3+
(22)
由式(8)和式(13)推导滤波误差的导数为
(23)
由式(23)可知,存在非负连续函数B2、B3,满足不等式
(24)
(25)
则可得
(26)
假设V(0)=p,当V≤p成立时,考虑紧集
(27)
(28)
其中,χ是足够大的正数。故此时Ω1×Ω2也是紧集。由此可知,在V≤p成立时,Bi(i=2,3)在Ω1×Ω2上有最大值,记为Mi。
由于ρ3≥|Δ|,可得
(29)
此时,对式(22)进一步处理可得


(30)
故按如下条件设计控制参数
(31)
(32)
其中,d≥0为待设计的正数,此时
(33)
然后将式(33)两边同乘以e2dt,再在[0,t]上对其积分得
(34)
故可得闭环系统状态是有界的,并且当ε充分小时,可以保证系统跟踪误差足够小。实际应用中,采用人工试错方式进行调参,在很大程度上依赖于调试人员的经验,比较繁琐。本文采用深度强化学习方法设计控制器参数的智能优化算法,实现对弹道倾角指令的跟踪。
2.2 基于深度强化学习的高超声速飞行器控制器参数优化设计
2.2.1 马尔可夫决策过程
本文的姿态控制问题符合马尔可夫性,即未来状态的概率分布仅依赖于当前状态。按照马尔可夫决策过程,在时刻t的状态值可仅依靠上一时刻t-1的状态值由式(1)得到。此时,假设遵循策略π(S),控制参数为k=π(S),可以得到下述轨迹
S0,k0,R0,S1,k1,R1,……,St,kt,Rt,……
(35)
其中,Rt为t时刻的奖励值。St和kt分别为
St=[S1t,S2t,S3t]T,kt=[k1t,k2t,k3t]T
(36)
其中,St为在t时刻的状态向量;kt为在t时刻的动作值向量。Sit和kit分别表示在t时刻Si和ki的值,i=1,2,3。问题就转化为了寻找一个最优策略π*(S),使得控制过程中的跟踪误差和控制量消耗最小。即在采取最优策略得到的式(35)的轨迹中,其奖励值总和最大。
为了衡量策略函数在给定状态时采取动作的优劣,定义回报Gt为t时刻开始往后所有奖励的衰减总和
(37)
其中,γRL为折扣因子。定义状态动作值函数Q(St,kt)为在状态St下采取动作kt会收到的回报,由式(37)可得

(38)
这样当前时刻的状态动作值函数就可以由下一时刻的状态动作值函数计算得到。
2.2.2 DDPG控制参数寻优算法
根据文献[11],构建4个神经网络,且Critic网络输出值为Q(St,kt|θ),θ为该评价网络的权值参数;Critic目标网络输出值为Q′(St,kt|θ′),θ′为该目标评价网络的权值参数;Actor当前网络输出值为π(St|φ),φ为该策略网络的权值参数;Actor目标网络输出值为π′(St|φ′),φ′为该目标策略网络的权值参数。
在训练中的探索部分,利用策略网络π(St|φ)输出原始动作值并与噪声叠加得到kt与环境交互
kt=π(St|φ)+N
(39)
其中,N为引入的OU噪声以增强对环境的探索,然后将与环境得到的样本(St,kt,Rt,St+1)存入经验回放池D中。在网络更新部分,为实现深度神经网络训练时要求的样本无关性,从经验回放池中随机取出N个样本进行训练。假设n=1,2,3,…,N,对随机取出的样本重新编号为(Sn,kn,Rn,Sn+1)。Q(Sn,kn|θ)的目标是拟合下列目标函数
yn=Rn+γRLQ′(Sn+1,π′(Sn+1|φ)|θ′)
(40)
此时,损失函数为最小化均方误差
(41)
然后,采用梯度下降方法完成对Critic网络的更新。
为了使Actor网络不断地向更优的策略拟合,则其更新方向需按照使Q(Sn,kn|θ)增大的方向进行优化。其梯度更新公式为
(42)
其余2个目标网络则在每个训练回合完成后进行软更新
θ′←τθ+(1-τ)θ′
φ′←τφ+(1-τ)φ′
(43)
其中,τ∈(0,1)为惯性参数。
整个控制结构如图1所示。

图1 高超声速飞行器智能控制框图Fig.1 Hypersonic vehicle intelligent control block diagram
综上所述,基于DDPG的高超声速飞行器智能优化算法训练过程如表2所示。

表2 基于DDPG的高超声速飞行器智能优化算法
3 仿真分析
3.1 DDPG智能体训练
选用飞行参数[19]为速度V=4590m/s,质量m=1.378×105kg,转动惯量I=9.5×106kg·m2,大气密度ρ=0.0125368kg/m3,平均气动弦长c=24.4m,参考面积S=335.2m2,地心距r=6.4×106m。式(1)中取Δ=0.01sin(0.2t)rad/s2,其余参数取ρ3=0.01,ε=0.01,μ=3.936×1014,d=0.5。低通滤波器的时间常数为τ2=0.01,τ3=0.1。选择跟踪目标为γd=10sin(0.1t)°。训练中高超声速飞行器的各变量约束如表3所示。

表3 高超声速飞行器的状态约束
Actor网络隐含层中使用三层全连接网络;Critic网络隐含层中同样使用全连接网络。Actor网络的输出层激活函数采用tanh函数g1(z),使其输出位于(-1,1)之间,以此保证控制输入约束在容许范围内,除此之外其余网络的激活函数均选择使用Relu函数g2(z)作为激活函数
(44)
训练的相关参数如表4所示。

表4 训练参数设置
奖励函数的设置是强化学习训练的关键,结合本文问题,将奖励函数R设计为如下形式
(45)
式中,ks是跟踪误差权重系数,ku是控制量权重系数;γmax、δmax分别为弹道倾角和升降舵偏转角所设定的最大值;Ra是奖励函数中引入的控制量变化率
(46)

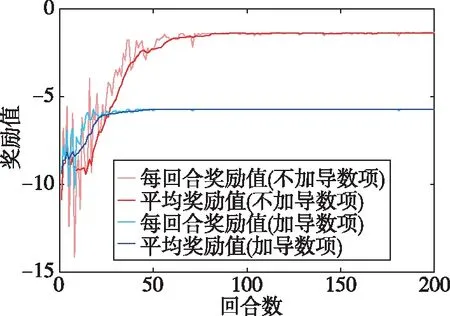
图2 奖励曲线Fig.2 Reward curve
由图2可知,在奖励函数未加导数的情况下,奖励曲线在第74回合之后奖励值到达并保持在终值的5%误差以内;而在加入奖励导数项之后,奖励曲线在第25回合就达到了上述标准,并且后者的曲线在前几个回合内的奖励值更加平稳。
3.2 姿态控制仿真结果
图3~图6所示为标称情况下的控制效果。由图可以看出,在加入导数项后,加快训练速度的同时能够保证控制效果。

图3 弹道倾角跟踪曲线Fig.3 Flight path angle tracking curve

图6 升降舵偏转角变化曲线Fig.6 Elevator curve
为了验证所设计控制器对参数不确定性的适应能力,对气动参数在标称值±50%内进行拉偏处理,执行300次蒙特卡罗仿真实验,实验结果如图7和图8所示。从图中可以看出,在系统存在不确定性的情况下,控制算法可以适应系统不确定性带来的变化,具有较好的鲁棒性。

图4 攻角变化曲线Fig.4 Attack of angle curve

图5 俯仰角加速度变化曲线Fig.5 Pitch angle curve

图7 不确定条件下弹道倾角变换曲线Fig.7 Flight path angle curve under uncertainty

图8 不确定条件下舵偏角变换曲线Fig.8 Elevator curve under uncertainty
4 结 论
本文针对高超声速飞行器姿态控制问题,设计了一种基于DRL的动态面智能优化控制算法。通过结合DRL机制的寻优思想,完成对动态面控制的参数智能寻优,代替了传统的参数调整过程与时间消耗,构建出智能控制器。经仿真结果表明,该控制器可以在考虑控制量消耗的情况下实现高性能的稳定跟踪控制,且在考虑气动参数不确定性情况下仍能保持良好的跟踪效果。
