基于时变AR 模型的MEMS 陀螺抗野值Kalman 滤波

管可可, 王怀野, 霍明磊

（北京航天飞腾装备技术有限责任公司, 北京 100094）

0 引言

稳定平台作为框架式导引头的重要组成部分,其性能直接影响导引头的制导精度［1］。 陀螺是控制稳定平台和解算视线角速度的重要器件, 弹上常用的陀螺有挠性陀螺、 光纤陀螺、 激光陀螺、 微机械陀螺（Micro Electro Mechanical System, MEMS）等, 其中的MEMS 陀螺因成本低、 体积小、 质量小以及功耗低等优点被广泛应用于低成本的小型框架式结构导引头［2］。 图1 为一款应用了MEMS陀螺的导引头内部结构。

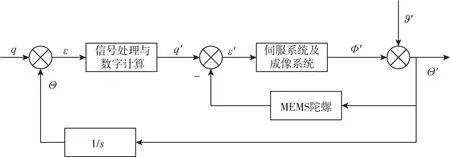
图1 导引头内部结构图Fig.1 Internal structure diagram of the seeker

图1导引头伺服控制中的MEMS 陀螺作为速率稳定内环的反馈器件, 输出数据直接影响整个导引头系统的控制品质。 在实际应用过程中采用传统PID 控制器时, 由于MEMS 陀螺输出数据噪声大, 如果不经过滤波, 微分项会使得控制量有明显的随机波动, 导致系统发散。 所以需要对导引头稳定平台的MEMS 陀螺数据进行滤波, 使其数据更加平稳, 且延迟必须要小。

针对MEMS 陀螺噪声大、 滤波后有延迟等问题, 国内外许多学者对此进行了研究。 文献［3］利用自回归滑动平均模型对MEMS 陀螺误差进行建模, 并利用Kalman 滤波对误差进行补偿, 但是建模前需要对MEMS 陀螺数据进行许多预处理。 文献［4］ 利用随机加权最小二乘算法有效抑制了MEMS 陀螺的噪声, 但是系统延时不好。 文献［5］通过对MEMS 陀螺数据建立时间序列ARMA 模型并采用多次Kalman 滤波对陀螺随机漂移进行补偿,MEMS 陀螺噪声随滤波次数增加而减少, 但是运算量会明显加大。 文献［6］利用Kalman 滤波对风速风向的MEMS 陀螺进行处理, 延时问题得到明显改善, 但是滤波效果不如加权滑动均值滤波。 文献［7］利用高阶自回归模型（Autoregressive, AR） 对陀螺随机误差进行建模, 但扩大滤波器维数可能会导致滤波不稳定甚至发散。 文献［8］也利用Kalman 滤波对随机误差进行补偿, 但是量测噪声方差和系统噪声方差均由简单统计得到, 无法跟随实际变化。

Kalman 滤波因其滤波效果好、 延迟低在工程中应用比较广泛, 但Kalman 滤波的效果与其模型的精确度成正比关系［9］, 固定的AR 模型不仅需要经过大量预处理才能得到精确模型参数, 而且对于陀螺实时输出数据的拟合度无法保证, 这无疑会降低Kalman 滤波的实时效果。 因此, 本文提出一种新的方法: 利用遗忘因子递推最小二乘实时建立AR 模型, 并将这种时变的AR 模型应用到抗野值Kalman 滤波中, 通过与抗野值Kalman 滤波对比发现延时更小, 各项噪声系数明显降低。

1 遗忘因子递推最小二乘与抗野值Kalman 滤波结合

Kalman 滤波的系统模型越精确, 滤波效果越好。 利用遗忘因子α对历史数据进行加权, 使历史数据的影响被减弱, 使新数据的权值增大, 递推最小二乘递推得到的AR 模型参数实时性更好,使模型参数能更好地反映信号的动态特征。 利用遗忘因子递推最小二乘建立的时变AR 模型可以很好地解决因为抗野值Kalman 滤波系统模型不精确而导致的滤波效果降低问题, 同时加入了抗野值的Kalman 滤波又能降低野值对滤波结果的影响,使滤波效果再次提升。

1.1 基于遗忘因子递推最小二乘的自回归AR 模型参数实时更新

AR 模型一般采用最小二乘进行参数估计, 但最小二乘不仅运算量大, 而且无法用于在线辨识,无法实时给出MEMS 数据的AR 模型参数。 递推最小二乘无矩阵运算, 能大幅减少计算量和存储量,可实现在线辨识。 随着参数的迭代, 辨识的结果也越来越精确。

式（1） ～式（5）中,α为遗忘因子, 一般取值范围为［0.95, 1］;θk、θk+1、分别为递推最小二乘第k次和第k+1 次迭代的系数解以及第k+1 个估计值;yk+1为第k+1 个观测数据;hk+1为第k+1 次更新的观测数据矩阵;Pk、Pk+1分别为第k次和第k+1 次系统协方差;Gk+1为第k+1 次迭代的增益矩阵;ek+1为方程误差。 为了在工程上减少计算量, 故采用一阶AR 模型。

1.2 自适应抗野值Kalman 滤波

MEMS 陀螺的输出信号中含有较多的野值, 如果不采取措施去除这些野值, 将对Kalman 滤波效果造成不小的影响。 所以本文采用了一种自适应抗野值的Kalman 滤波, 这种方法能在Kalman 滤波的基础上进一步对滤波增益和预测值进行修正,使滤波效果更好。

根据遗忘因子递推最小二乘得到的时变AR 模型参数θk-1, 可以得到Kalman 滤波状态方程的状态转移矩阵Φk,k-1

预测过程如下

更新过程如下

式（6） ～式（12）中,Xk,k-1为系统状态向量tk-1时刻到tk时刻的一步预测值,Pk-1与Pk为tk-1、tk时刻系统均方误差阵,Pk,k-1为tk-1时刻到tk时刻系统均方误差阵的一步预测值,Kk为tk时刻的卡Kalman 滤波增益。

式（13）、 式（14）中,εk为tk时刻系统的最优估计值与实际观测值的误差, 序列ε为 {ε1,ε2, …,εk},E（ε）为序列ε的均值,Sk为序列ε的方差。 令, 其中的为前k时刻序列ε的标准差。

2 实验结果与分析

导引头所用的滤波器对延时和滤波效果要求比较高, 利用变幅值、 变周期的正弦波对时变AR模型的抗野值Kalman 滤波进行仿真测试, 可以分析滤波器的延时、 信噪比和滤波效果, 其仿真结果如图2 所示。

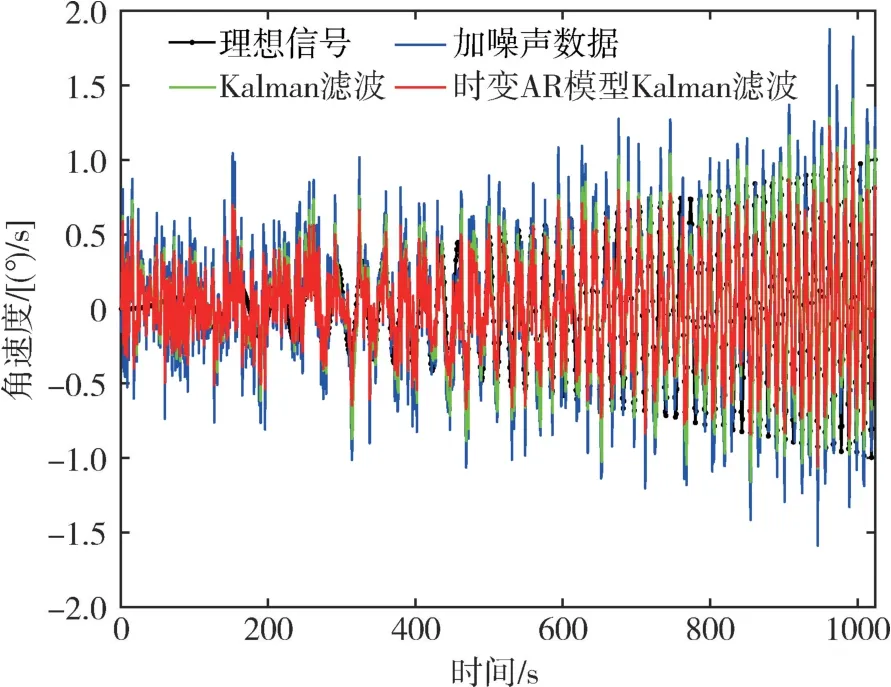
图2 仿真滤波前后对比Fig.2 Diagram of comparison before and after simulation filtering

图2 的仿真测试是在真实数据基础上加入信噪比为3dB 的零均值白噪声来模拟陀螺输出数据。Kalman 滤波虽然能滤掉大部分噪声, 但是对野值滤波效果不好, 滤波后的曲线受野值影响较大;而时变AR 模型的抗野值Kalman 滤波不仅能有效降低野值干扰, 且延迟相对Kalman 滤波更小。

对MEMS 陀螺输出的原始数据进行抗野值Kalman 滤波和时变AR 模型的抗野值Kalman 滤波,根据滤波后数据的均值方差以及Allan 方差的各项噪声系数来对比滤波效果, 图3 为滤波对比数据曲线。

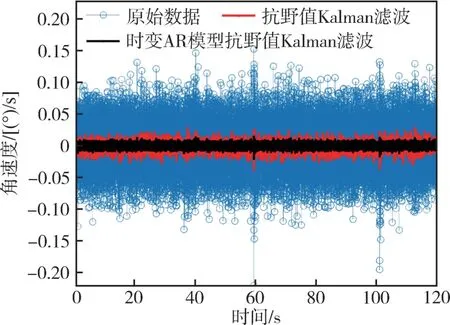
图3 MEMS 陀螺数据滤波前后对比Fig.3 Comparison of MEMS gyroscope data before and after filtering

由图3 可知, 时变AR 模型的抗野值Kalman滤波输出更稳定, 且对于野值的抗干扰性能更好。表1 为几种方法滤波前后的均值和方差对比。

表1 中, 抗野值Kalman 滤波不会降低陀螺输出均值, 而其方差降低了70.9%; 经过时变AR 模型的抗野值Kalman 滤波后, MEMS 陀螺输出均值降低了83.0%, 方差降低了83.5%。 从数据上看,时变AR 模型抗野值Kalman 滤波更具有优势。 Allan 方差对比结果如图4 和表2 所示。

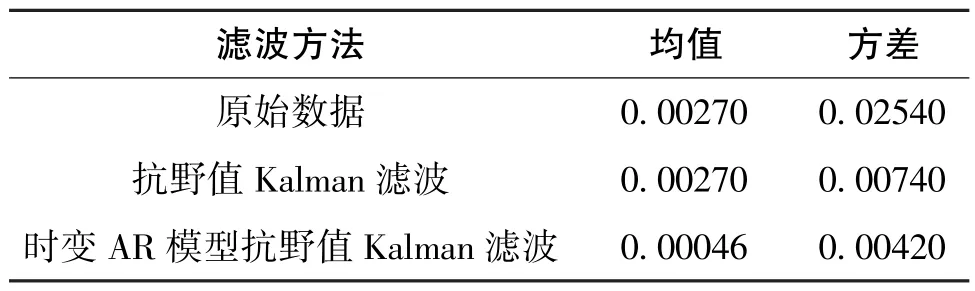
表1 滤波前后均值和方差对比Table 1 Comparison of means and variances before and after filtering

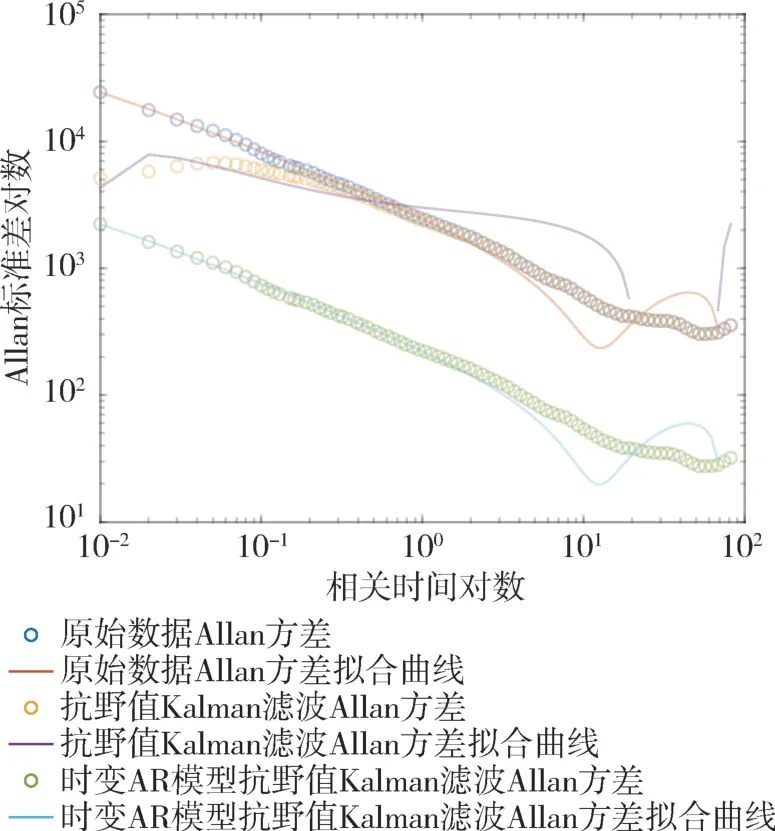
图4 Allan 方差对比结果Fig.4 Comparison results of Allan variance

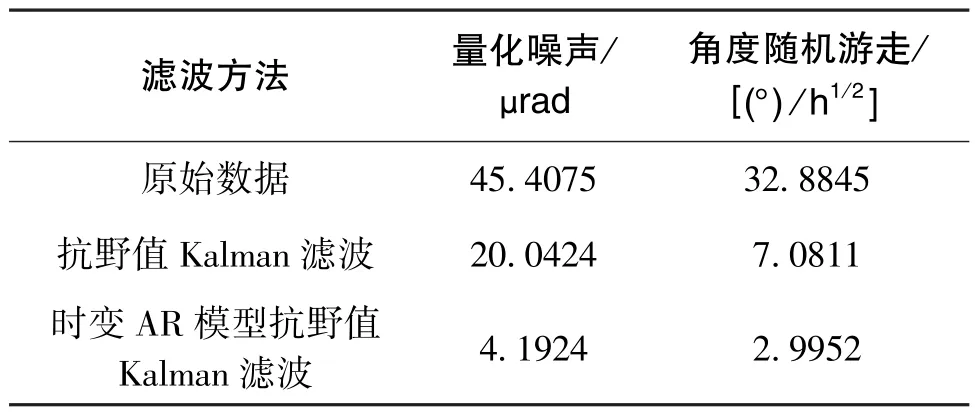
表2 滤波前后噪声项对比Table 2 Comparison of noise terms before and after filtering

表2 中, 经过抗野值Kalman 滤波之后, 原始数据的随机误差得到了改善, 降低了50%以上;而时变AR 模型的抗野值Kalman 滤波效果更为明显, 随机误差降低了90%以上。

将时变AR 模型的抗野值Kalman 滤波加入到导引头伺服控制回路进行闭环实验, 结果如图5所示。

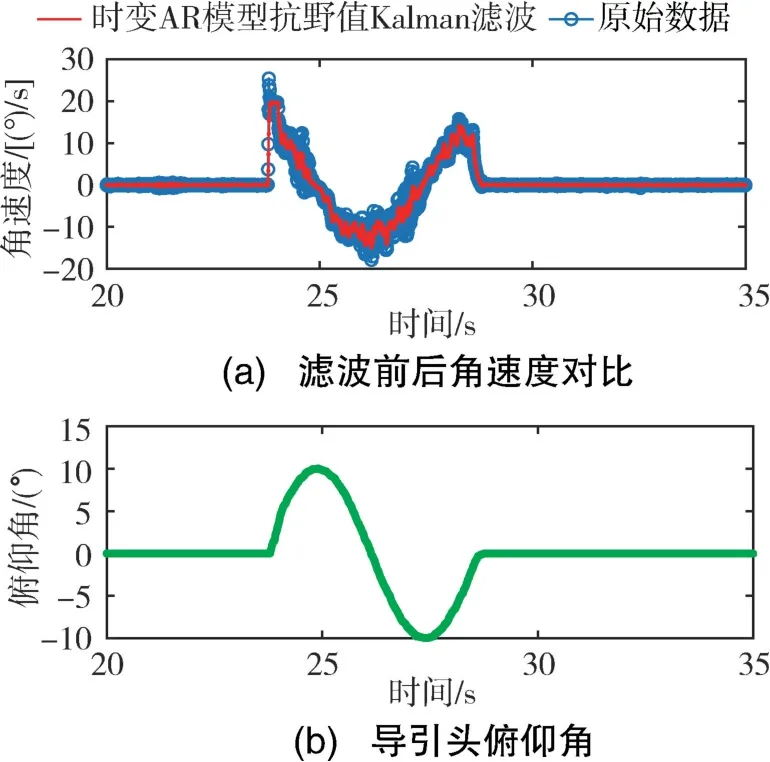
图5 导引头闭环测试Fig.5 Diagram of seeker closed-loop test

由图5 可知, 在导引头的闭环测试中, 导引头能够稳定控制框架角, 从而稳定跟踪目标, 验证了时变AR 抗野值Kalman 滤波延迟小、 能有效降低MEMS 陀螺噪声等特点。

3 结论

为了减少MEMS 陀螺输出的随机误差对导引头伺服控制回路的影响, 本文提出了基于遗忘因子递推最小二乘进行时变AR 模型建模并与抗野值Kalman 滤波相结合的方法, 不仅能减少因系统模型不精确造成的影响, 还能降低野值对导引头伺服控制的干扰。 通过实验可以得到, 经过时变AR模型抗野值Kalman 滤波, MEMS 陀螺数据的均值、方差降低了80%以上; Allan 方差的各个噪声项均比原始数据降低了90%以上, 测试结果均优于抗野值Kalman 滤波。 时变AR 模型抗野值Kalman 滤波方法在导引头伺服控制回路的闭环测试中效果良好, 具有很好的工程应用前景。