深空探测自主导航技术综述

强祺昌, 林宝军,4, 刘迎春, 林 夏

（1. 中国科学院微小卫星创新研究院, 上海 201203; 2. 中国科学院大学, 北京 100049;3. 上海微小卫星工程中心, 上海 201203; 4. 上海科技大学信息科学与技术学院, 上海 201210）

0 引言

从1958 年美国和前苏联启动探月计划开始,世界发达国家和航天技术大国已经开展了100 多次深空探测活动［1］。 进入21 世纪, 许多国家纷纷制定了深空探测计划, 如美国的“Artemis” 载人登月计划［2］、 欧洲的 “Aurora” 载人登陆火星计划［3］、 日本的“DESTINY + ” 深空技术验证计划［4］、 印度的“Shukrayaan” 金星探测计划［5］等。截止至2020 年, 我国成功完成了 “嫦娥系列”6 次无人探月任务, 实现了“绕”、“落”、 “回”三步走战略, 代表着中国探月三期工程圆满收官［6］。 2020 年7 月, 我国首个火星探测器“天问一号” 成功发射升空, 完成了对火星的绕飞、 着陆、 巡视探测任务［7］。 我国规划在2030 年前后实现载人登月, 在2033 年启动首次载人火星探测任务, 长期目标是在火星建立永久性居住点。

由于地球轨道任务的探测距离较近, 基于地面测控网的卫星导航系统可以实现较高的定位精度。 但是深空探测任务的飞行时间长、 距离远、环境复杂多变, 传统的无线电测量技术会出现通信时延长、 传输效率低、 天体遮挡等问题, 无法对深空探测器进行实时控制。 当导航或通信系统出现突发故障时, 通信时延给深空探测器的安全生存问题带来了潜在的威胁［8］。 因此, 为了满足深空探测任务的导航需求, 探测器需要具备自主执行部分或全部导航功能的能力。 自主导航技术不需要地面测控网频繁介入, 利用星载敏感器即可实时获取本体的在轨状态, 已成为深空探测领域的关键技术之一。 当探测器与地面站通信中断时,自主导航技术仍然能够进行精确的轨道确定、 轨道保持等操作, 大大提高了探测器的在轨应用潜力。

从深空探测任务的实际工程需求出发, 自主导航方法可以分为天文导航、 惯性基组合导航以及星间测量导航等三类方法。 天文导航是一种比较成熟的深空自主导航方法, 具有全自主、 抗干扰能力强等优点, 已成功应用于Deep Space-1、Deep Impact 等深空探测任务［9］。 惯性基组合导航是一种不依赖于外部信息的自主导航方法, 具备短时精度高、 不易受环境影响等优点, 常常与其他导航方法组合使用, 辅助提高导航定位精度［10］。近些年, 国内外学者对星间测量导航技术进行了大量的理论分析和仿真验证, 表明该技术可以有效减轻探测器对地面站的依赖, 并有望脱离地面测控网实现深空探测器自主导航［11］。

本文从技术原理、 研究现状和关键技术方面对天文导航、 惯性基组合导航和星间测量导航进行了介绍与分析, 最后结合深空自主导航技术发展态势对我国深空探测自主导航技术发展给出了若干建议。

1 天文导航

深空探测任务中, 根据采用不同种类的测量信息, 天文导航分为天文测角导航、 天文测速导航和天文测距导航（脉冲星导航）。 由于原理简单、易于实现, 天文测角导航常常应用于天体转移段和进近段的自主导航任务。 天文测角导航主要包括四类光学观测量:1) 视直径和质心; 2) 地平线与参考星的夹角; 3) 地表特征与参考星的夹角;4) 行星/月球掩星时间。 前两种观测量常常应用于天文测角导航系统, 如Mariner-9 号、 Voyage 号和Deep Space-1 号等深空任务。

1.1 技术原理与研究现状

（1）天文测角导航

天文测角导航利用行星和恒星等已知星历的天体之间的角度关系进行自主导航［12］。 如图1 所示, 探测器利用光学敏感器确定以地球为天顶、恒星方位为轴的两个圆锥面, 再利用太阳方向矢量确定第三个圆锥面, 根据三个曲面的交线确定自身的轨道状态［13］。 天文测角导航的优点是原理简单、 计算简便、 易于实现, 缺点是导航精度随探测器与导航星之间距离的增加而降低。

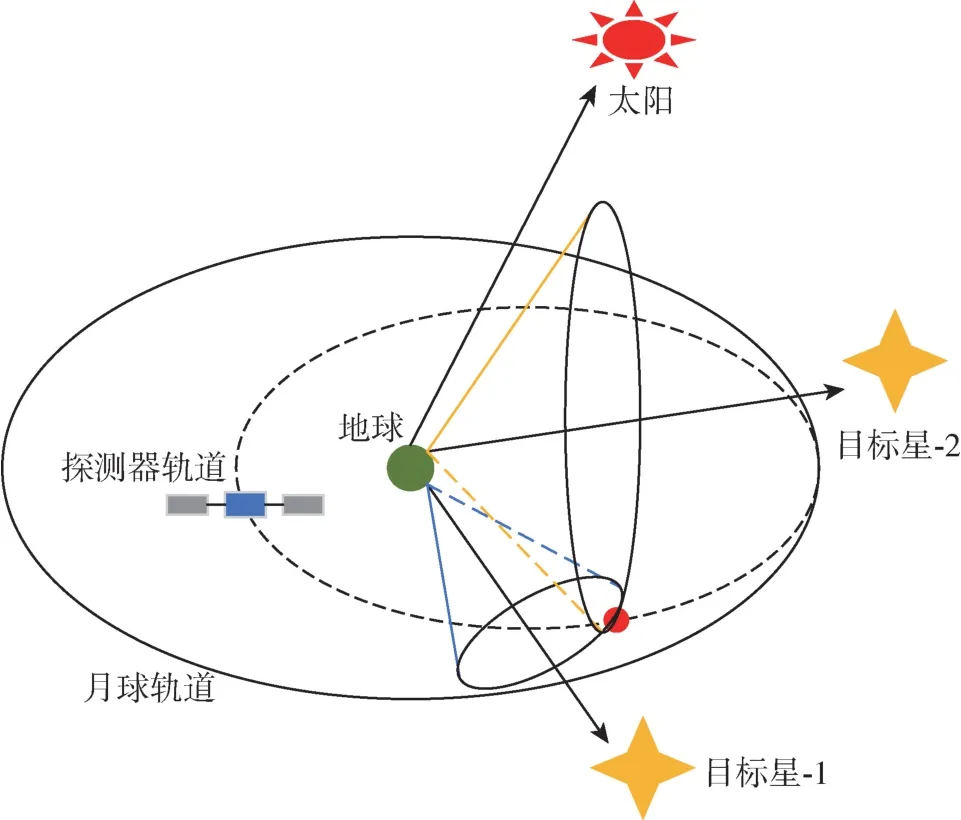
图1 天文测角导航原理Fig.1 Principles of astronomical angle measurement navigation

在国外, 1968 年美国发射的Apollo-8 飞船率先应用了这一理论, 将六分仪作为光学导航敏感器辅助校正探测器的轨道信息, 第一次验证了天文测角导航技术的可行性［14］。 1971 年, Mariner-9号探测器仅利用火卫一、 火卫二和恒星之间的光学观测量实现了火星轨道插入段的自主导航, 再次验证了天文测角导航技术的有效性［15］。 此外,美国的ViKing 号［16］、 Voyage 号［17］等深空探测器也都应用了天文测角导航技术, 但早期的天文测角自主导航任务需要将光学观测量传回地面处理,后再上传指令回深空探测器。 直至1998 年, 美国发射的Deep Space-1 号探测器第一次真正在轨验证了巡航段的光学全自主导航, 位置精度和速度精度分别达到250km 与0.5m/s, 能够满足巡航段的导航精度要求［18］。 从深空一号开始, 美国的Mars Surveyor 号［19］、 Deep Impact 号［20］等 深空探 测任 务均在轨应用了自主天文测角导航技术。 表1 总结了天文测角导航技术在国外深空探测任务中的应用情况。

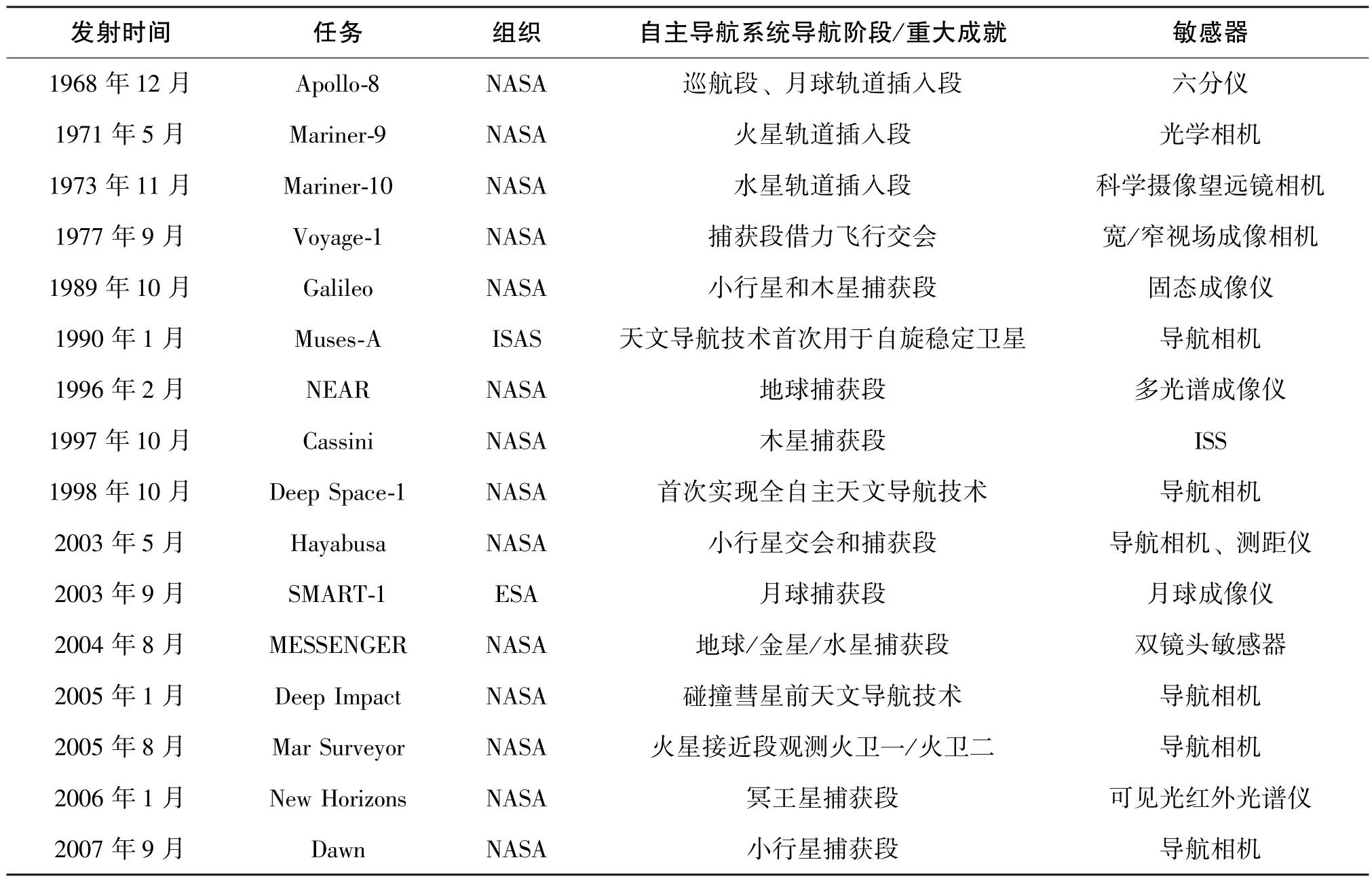
表1 国外的天文测角导航技术应用Table 1 Application of astronomical angle measurement navigation technology abroad

在国内, 2020 年我国发射的嫦娥五号［21］和天问一号［22］探测器搭载光学敏感器和惯性单元, 在转移段和接近段组合使用天文测角导航与惯性导航, 成功在轨应用了天文测角导航技术。 我国计划于2023 年发射的嫦娥六号探测器也将采用星上光学敏感器和地面甚长基线测量结合的导航方式。

（2）天文测速导航

天文测速导航的理论依据是光学多普勒效应。探测器在远离或接近目标天体的过程中, 光的频率会相应地变小或变大［23］。 如图2 所示, 根据光谱偏移量, 探测器可以解算出自身相对于目标天体的空间速度矢量［24］。 假设探测器位于相对恒星静止的位置, 代表天文光学信息恒定, 恒星光谱的波长用λ′表示。 当探测器与恒星的相对位置发生变化时, 星载光谱仪观测到波长漂移, 用Δλ表示。 基于多普勒原理, 波长漂移量与波长之比等于视向速度v与光速c之比［25］, 即

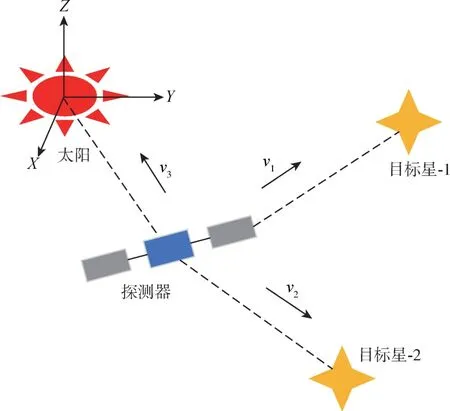
图2 天文测速导航原理Fig.2 Principles of astronomical velocity measurement navigation

在国外, 1960 年美国学者Franklin 等［26］研 究了来自恒星和行星际空间的光谱辐射特征, 首先提出了根据多普勒效应测速的想法, 并得到了预期的测量精度。 为了实现深空自主导航, 2000 年Yim 等［27］提出了天文测速/测角组合导航方法, 得出了仅根据径向速度不能估计全轨道状态的结论,需要结合径向速度观测量和相对于太阳的视线矢量实现自主导航, 通过仿真验证获得了优于3km的位置精度。 但是, 天文光谱测速导航还需突破诸多技术难点, 如建立准确的光谱源模型、 光谱频移的高精度测量以及可用谱线的遴选等技术,才能建立一套原理清晰、 可靠性高、 系统完整的技术方案。 2002 年, Henderson 等［28］基于多普勒频移测速原理成功研制了探测器轨道确定物理仿真系统, 可用于仿真验证天文测速导航系统的性能。2010 年, Greetham 等［29］提出了一种高亮度、 时间分辨光谱仪——ULTAR, 可与一系列先进的时间分辨线性和非线性振动光谱技术一起使用。 2011年, Abramov-Maximov 等［30］结合光学和无线电观测对太阳振荡运动进行了研究。

在国内, 2013 年张伟等［31］首次提出了天文光谱测速导航的想法: 在没有地面辅助的条件下,探测器利用光谱频移量获取相对目标天体的速度信息实现深空自主导航。 目前, 国内的天文测速导航技术已经取得了多方面的进展。 误差传递方面, 尤伟等［32］给出了特定条件下的定速误差均值与方差的解析表达式, 并得出天体视线方向两两正交导致的测速误差影响最小的结论。 时空基准方面, 张恒等［33］分析了时间误差在组合导航系统中位置估计和速度估计的工作原理, 基于内插外推时间匹配法则, 实现了测角/测速敏感器量测信息的同步。 组合导航方面, 尤伟等［34］提出了天地联合导航方法, 引入探测器与恒星的视向速度作为新增观测量, 使探测器位置估计精度提升了近一倍。 Liu 等［35］提出了天文光谱测速与天文测距组合导航系统, 有效增强了导航系统的鲁棒性。 性能评估方面, Chen 等［36-37］提出了测角/测速组合导航策略, 并开发了硬件在环导航仿真系统, 验证了方法的可行性和正确性。

（3）天文测距导航（脉冲星导航）

根据光速不变性, 天文测距导航系统通过比较探测器相对脉冲星的脉冲到达时间（Time of Arrival, TOA）测量值与预测值, 解算出探测器的轨道状态［38］。 如图3 所示, 探测器接收脉冲信号的时间计为t, 相位时间模型预报的脉冲到达参考点（太阳）的时间计为T, 二者之差乘以光速c即为探测器在脉冲星方向上的位置修正［39］。

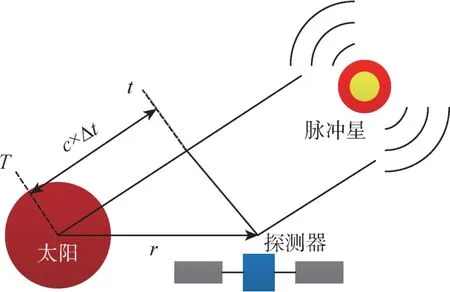
图3 天文测距导航原理Fig.3 Principles of astronomical ranging navigation

在国外, 1974 年美国喷气推进实验室的Downs博士［40］首次提出了X 射线脉冲星应用于深空自主轨道确定的想法。 1981 年, Chester 和Butman［41］进行了X 射线脉冲星导航模拟实验, 导航精度可以达到150km。 通过对比探测器采用X 射线敏感器与使用射电脉冲信号进行导航, 得出后者的导航精度更高但工程应用中无法满足其硬件需求的结论。 2005 年, Sheikh 等［42］提出了混合脉冲星的测量方法, 以确定不同轨道高度下探测器的位置和速度, 导航精度可以达到5km, 初步论证了天文测距导航方法的可行性。 根据Sheikh 博士的论文,深空探测任务中使用三颗脉冲星即可确定卫星的绝对位置, 第四颗脉冲星可用于机载时钟校准,进一步验证了天文测距导航方法的可行性和有效性［43］。

在国内, 2006 年帅平等［44］率先开展了X 射线脉冲星导航的研究工作, 并在国内已有的基础条件下初步论证了脉冲星导航的必要性和可行性。为了确保理论研究可以在工程中应用, 2016 年我国发射了脉冲星导航试验卫星（XP-NAV-1）, 主要用于验证X 射线脉冲信号的探测性能［45］。 2017 年,我国的首个空间X 射线天文望远镜发射升空, 在触发时间内成功监测到GW170817 伽马射线, 进一步验证了探测器利用脉冲星自主导航的有效性,为我国未来的脉冲星导航奠定了基础［46］。 2019 年,我国第一次开展了脉冲星导航试验, 中国科学院高能物理研究所开展了在轨X 射线脉冲星导航试验, 定位精度达到10km, 验证了X 射线脉冲星可用于自主导航任务［47］。 但由于我国缺乏专门用于脉冲星观测的望远镜以及各地观测条件的差异性,目前开展的脉冲星导航任务还不得不依赖于国外脉冲星数据库。

测角、 测速、 测距三种天文导航方法的特点归纳如表2 所示。

表2 天文自主导航方法对比Table 2 Comparison of celestial autonomous navigation methods

1.2 关键技术分析

（1）精确的轨道动力学建模

探测器在每个飞行阶段因不同的摄动影响具有不同的轨道特性, 如中心引力体非球形摄动、太阳及行星的多体引力摄动等［48］, 有必要针对各个飞行阶段建立高精度轨道动力学模型［49］。 高精度轨道动力学模型的建立需要考虑不规则行星引力场、 复杂的太阳光压、 行星高阶重力场等因素的影响, 例如采用天体的高阶重力模型代替质点重力模型、 对使用大型太阳电池阵的探测器建立太阳光压模型等操作, 以提高状态模型精度。

但是, 高精度轨道动力学模型过于复杂, 在实际工程应用中硬件系统很难满足大量的运算需求。 因此, 既满足精度要求又计算简便的动力学模型是深空自主导航系统的研究重点。

（2）高精度量测信息获取

探测器在深空中能利用的导航信息很少, 需要依赖自身搭载的各类敏感器获取有用的导航观测量。 因此, 量测信息的获取精度对深空自主导航性能有重要影响。

天文测角导航系统常常根据目标天体的视直径和质心观测量进行自主导航。 当探测器与天体之间的距离发生变化时, 天体在敏感器上的成像大小会有所不同, 需要图像处理方法能够自动识别并做出调整［50］。 图像获取与处理算法存在星点提取时间长、 内部星表存储量大等缺点, 因此快速捕获和星表压缩算法成为了重要的研究内容。目前, 常常采用星点聚类提取法对天体图像进行处理, 通过预处理和聚类操作优化天体测量信息的处理过程。

对于天文测速导航系统, 获取高分辨率、 高稳定性的光谱频移量是研究重点, 主要包括光谱预处理、 特征谱线提取和频移解算操作。 由于探测器飞行速度快、 恒星光谱信噪比低等因素影响,特征谱线提取是测量光谱频移量的关键技术。 光谱源模型精度决定了测速导航系统的状态估计性能, 影响模型精度的因素主要有目标恒星大气随机湍动、 局地爆发、 谱线热运动等［51］。

在天文测距导航系统中, 由于脉冲星信号极其微弱, 探测器通过测量光子的到达时间来估计脉冲TOA［52］。 估计脉冲TOA 的关键技术是计算观测脉冲轮廓与标准轮廓之间的时延, 目前的主流方法是利用相关函数计算二者的时间延迟, 虽然相关方法比较简单, 但是估计精度容易受信号频谱和噪声特性影响。 因此, 准确、 鲁棒性强的脉冲TOA 估计技术是脉冲星导航测量技术的重点研究内容。

为获取高精度的量测信息, 还需对以下方面进行深入研究: 1）提出新型测量原理解决微弱或复杂信号的量测问题; 2）提升导航敏感器的自主性以应对深空环境的不确定性。

（3）先进的导航滤波方法

深空探测自主导航系统属于非线性系统, 当前的导航滤波方法主要分为批处理法和递推法两类。 批处理滤波方法比较简单, 不需要了解先验信息, 已成功应用于Deep Space-1 和Deep Impact等任务。 但是对于复杂的轨道动力学模型参数估计问题, 这种方法并不适用。 递推处理滤波方法具备计算量小、 处理速度快、 实时性好等优点,已成为深空探测领域的主流导航滤波方法［53-54］。 对于高斯噪声、 非线性导航系统, 拓展卡尔曼滤波(EKF) 方法具有较好的滤波效果, 但由于引入了泰勒级数, 会出现截断误差, 导致性能不佳。 无迹卡尔曼滤波(UKF) 方法通过无迹变换计算随机变量的统计信息, 没有高阶项的截断误差, 可以获得更好的导航精度［55］。 对于非高斯噪声、 非线性导航系统, 粒子滤波方法的滤波性能更好,但会出现粒子退化现象, 消除粒子退化的关键技术是选择合适的密度函数或重采样［56］。 尽管上述滤波方法有效解决了非线性问题, 但需要准确的先验知识, 如状态估计、 测量误差等, 这些在导航系统中无法准确获得。

为提高自主导航系统的滤波性能, 还需重点研究以下内容: 1）导航系统采用先进的滤波理论,如神经网络理论、 模糊理论等; 2）提升导航滤波方法能够自适应不确定因素的能力。

2 惯性基组合导航

2.1 技术原理与研究现状

惯性导航系统（Inertial Navigation System, INS）由一组惯性器件（Inertial Measurement Unit, IMU）和计算单元组成, 在已知初始状态的条件下通过数值积分解算本体的位置、 速度和姿态信息。 INS 的特点是不依赖于外界信息, 也不向外界辐射能量,具有短时精度高、 隐蔽性好、 不易受干扰等优点,但导航精度会随着时间的推移而降低。 在深空探测中, 惯性导航是动力飞行段的主要导航方式。但由于惯性导航的精度随着时间的推移而降低,探测器仅利用惯性导航无法满足探测任务的导航需求, 需要与其他导航方法组合使用, 下面介绍三种常用的惯性组合导航方法:

（1）惯性/雷达/视觉相对测量组合

由于惯性导航具备自主、 短时精度高的特点,两个探测器为了完成精确的交会对接操作, 在彼此靠近的过程中常采用惯性导航方法。 但是, 探测器在逼近段可能存在初始导航误差, 需要其他导航方法修正惯导初始误差。 当两个探测器距离较近时, 多采用雷达、 相机等敏感器直接测量目标探测器, 利用测量结果修正惯导的加速度信息;当两个探测器距离较远时, 一般采用红外相机、激光测距仪、 激光雷达等敏感器与IMU 进行组合导航［57］。

（2）惯性/测距/测速导航组合

在天体软着陆过程中, 为了连续测量加速度和姿态角速度信息, 探测器常采用INS 作为核心导航方法, 并利用测距/测速导航方法修正惯性导航误差。 基于IMU/测距/测速的软着陆组合导航技术已成功应用于众多天体软着陆任务: 在国外, 如美国的Apollo［58］、 Surveyor 任务和苏联的Luna 系列月球软着陆任务, 还有美国的凤凰号和火星科学实验室的火星探测任务; 在国内, 2004 年我国正式开展“嫦娥系列” 月球探测工程, IMU/测距/测速组合导航在嫦娥三号、 嫦娥四号、 嫦娥五号软着陆任务中均发挥了关键作用, 高度和速度导航精度分别达到了分米和分米/秒的水平［59-60］。 2020年, 我国成功首发天问一号火星探测器, IMU/测距/测速导航方法再次成功应用于火星表面的软着陆过程, 速度精度达到了分米/秒的水平［22］。

（3）惯性/天文导航组合

在深空探测中, 探测器飞行时间长、 距离目标天体远, 很难获取高精度的天体量测信息［61］。由于惯性/天文组合导航方法具有独立性强、 隐蔽性高、 抗干扰能力强等优势, 该方法常应用于巡航段和进近段的自主导航任务, 如胜利者号、 水手号、 嫦娥五号等深空探测任务。 Ning、 Wu 和Zheng 等［62-65］均提出了惯性/天文测角组合导航方法, 利用光学敏感器测量结果修正惯导的位置误差、 速度误差和姿态误差, 并进行了硬件在环仿真试验验证。 Wang 等［10］提出了低推力行星际探测器自主导航方法, 利用脉冲星观测有效减小了惯导误差的长期影响。

2.2 惯导参数修正技术

随着积分时间的推移, 惯性导航系统的速度误差和位置误差变大, 需要利用其他测量信息来修正惯导参数。 在地月空间中, 探测器的自主程度因任务而异, 相应的惯导更新源会有所不同。如图4 所示, 基于光学测量信息, 探测器可以将自然天体、 被动表面信标或人造卫星等目标作为惯导更新源［66］。

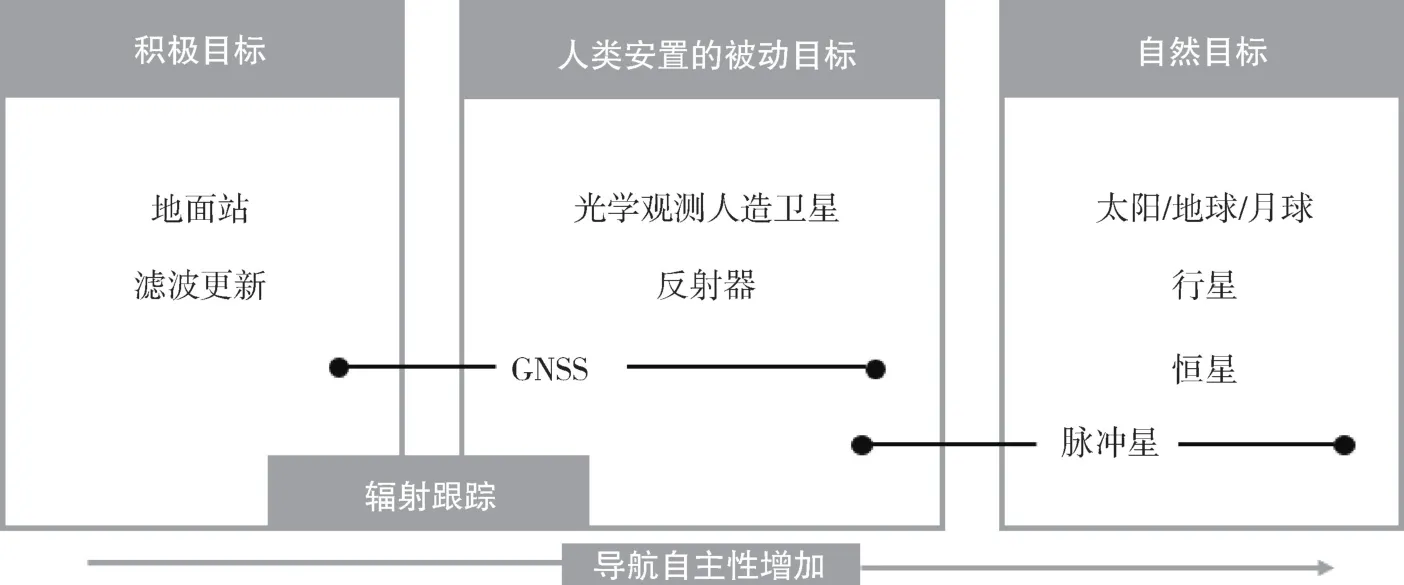
图4 地月空间惯导更新的解决方案Fig.4 Solution of the Earth-Moon space inertial navigation update

深空探测器利用自然天体作为惯导更新源有诸多优点, 如无需与地面站通信、 无需部署额外的天基资产、 有助于构建强大的导航架构等。 在地月空间中, 由于太阳、 地球或月球的运动特性已知, 最有希望成为惯导更新源。 探测器利用光学敏感器获取天体质心或亮度中心的位置信息,将测量值与自身位置信息相结合完成惯性导航参数修正。

由于近地空间人造卫星的轨道信息已知, 其作为惯导更新源能够提供更加准确的惯导修正信息［67］。 但可观测的卫星都围绕在地球附近, 深空探测器光学观测近地卫星存在几何形状变化不大的问题。 若存在垂直于地球视线的卫星加入光学观测过程, 则可以显著改善导航方案的性能。 目前, 已证明地月三角平动点附近的轨道比较稳定,可以将一颗或多颗卫星置于三角平动点轨道附近,以实现人造卫星作为惯导更新源的目标。

更复杂的方法是将地球或月球上的表面特征作为惯导更新源, Bowers 等［68］已经证明恒星、 地球或月球上已知地标之间的角度信息可用于顺月导航。 由于地球大气层遮蔽了地平线, 探测器只能观测到模糊的地平线特征, 但鉴于对地球大小、形状的了解, 可以通过表观直径来估计地球的表面特征。 基于表观直径估计方法, 探测器利用红外光波段观测二氧化碳层能够形成比可见光波段更清晰的地平线特征［69］。 与地球相比, 阳光照射的月球表面具有清晰的地平线, 可以相对容易地观测到月球表面特征或地平线位置［70］。

惯性导航作为自主导航系统的重要组成部分,根据深空探测任务的自主程度选择最优的惯导更新源和观测方法成为了研究重点。

3 星间测量导航

由于具有自主性高、 精度高、 原理简单等优点, 星间测量导航技术尤其是星间辐射跟踪导航技术将是未来深空探测领域的重要研究方向。 根据采用不同种类的测量信息, 星间测量导航方法可以分为星间辐射跟踪、 星间光学观测和量子定位方法。 目前, 采用星间测量导航技术的深空探测器比较少, 如美国的CAPSTONE、 MSL 任务。值得注意的是, 2022 年6 月美国发射的CAPSTONE 号探测器主要任务之一是测试与月球轨道器之间的星间测量联合定轨技术, 为Artemis 载人登月计划做好准备。

3.1 技术原理与研究现状

（1）星间辐射跟踪

星间跟踪观测（Satellite-satellite Tracking, SST）包括辐射距离观测和距离变化率观测, 具有原理简单、 精度高等优点, 可以为深空探测器自主导航提供技术支持［71］。 其中, 一类星间辐射跟踪方法是用于获取两个或多个探测器之间的相对轨道信息。 基于该方法的导航网络已成功用于深空探测任务, 如火星科学实验室（Mars Science Laboratory, MSL）和CAPSTONE 任务。 MSL 任务以MRO 和Odyssey 探测器作为导航信标, 通过超高频星间测量信号进行轨道确定, 辅助探测器在火星进近、进入、 下降和着陆阶段进行自主导航［72］。 CAPSTONE 任务将在月球进近段与月球轨道器进行星间联合定轨测试, 目前该探测器还在前往月球的飞行途中［73］。

LiAISON（Linked Autonomous Interplanetary Satellite Orbit Navigation）是另一类星间辐射跟踪方法,可以确定两个或多个探测器的相对和绝对轨道信息。 LiAISON 方法要求星间测量导航网络中至少有一颗卫星位于大小、 形状和方向唯一的平动点轨道（Libration Point Orbit, LPO）上, 如地月空间中的Halo 轨道或Lissajous 轨道等［74］。 在不依靠地面站的情况下, 由于LPOs 具有很强的非对称性, LiAISON 方法能够同时估计出参与探测器的相对和绝对轨道信息, 实现深空探测器自主导航。 在地月空间中, LiAISON 方法应用于地月转移段的演示,如图5 所示。

图5 LiAISON 方法应用于地月转移段Fig.5 LiAISON method applied to the Earth-Moon transition segment

在国外, 2005 年Hill 等［75］首次提出了LiAISON 概念, 为实现探测器在地月空间中的自主导航提供了一种可行方案。 2007 年, Hill 等［76］在三体不对称引力场中利用标量SST 数据同时估计探测器的轨道信息, 再次验证了使用LiAISON 方法进行轨道确定的可行性和有效性。 2008 年, Hill等［77］进行了月球导航模拟试验, 平动点轨道器与环月轨道器分别可以实现100m 和10m 的导航精度, 可以满足深空探测导航精度要求。 联合地面导航方面, 2013 年Leonard 等［11］提出了联合使用地面跟踪和LiAISON 的自主导航方法, LiAISON 方法不仅改善了探测器的自主性, 还提高了深空导航精度, 可以将地面跟踪站的数量从6 个减少到3个, 有效减轻了地面测控压力。

在国内, 建立深空导航星座方面, Xin、 Zhang和Gao 等［78-80］提出了基于LiAISON 技术构建深空导航星座的方法, 验证了用户卫星与平动点轨道星座之间进行辐射跟踪自主导航的可行性。 误差分析方 面, 2019 年Wang 等［81］评 估 了LiAISON 方 法受动态模型误差和时钟误差的影响, 特别考虑了非高斯随机噪声的影响。

（2）星间光学观测

深空探测器通过星间光学观测进行自主轨道确定也是一种星间测量导航方法。 与LiAISON 方法的原理类似, 该方法要求导航星的绝对位置已知, 利用光学观测量解算用户探测器的轨道信息［82］。 例如在地月空间中, 探测器利用光学敏感器观测一定数量的地球静止轨道（The Geostationary Orbit, GEO）卫星, 根据多颗GEO 卫星的几何形状和多种三角测量技术, 实现深空探测器自主轨道确定。

目前, 有关星间光学观测导航领域的研究还比较少。 在国外, 2009 年Christian 等［67］首次说明了GNSS 卫星是地月空间中的有效观测类型, 基于星间光学测量原理, 可以实现深空探测器光学自主导航。 2020 年, Bradley 等［83］通过光学观测月球中心、 月球地标、 人造卫星和行星, 评估了地月空间中的光学导航性能, 表明人造卫星是地月空间非常有效的观测类型, 利用中等性能的相机即可实现地月光学自主导航。 2021 年, 美国军方对外公布: 基于星间光学测量原理, Rhea 太空活动公司、 普渡大学、 军刀航天公司将联合为地月空间开发一个自主导航模块（Jervis Autonomous Module, JAM）, 配备JAM 的探测器可以在未被监测的太空区域以无线电静默方式自主运行数月。 由于具有突出的自主性和抗干扰能力, 星间光学观测导航是一种有效的深空自主导航方案。

（3）量子定位

与GPS 原理相似, 量子定位导航系统（Quantum Positioning System, QPS）用量子纠缠光取代了GPS 中的电磁波, 通过测量相互关联的两束纠缠光之间的到达时间差（Time Difference of Arrival,TDOA）解算卫星与用户的距离以及用户的空间坐标［84］。 与传统定位系统相比, 量子定位系统具有精度高、 保密性好等优点。 但是, QPS 技术的研究进展比较缓慢, 需要积累更多的理论基础和试验验证经验, 以实现导航领域的跨越式发展。

3.2 关键技术分析

（1）平动点轨道高精度建模

近地空间的导航星座具有旋转不可观测性,故仅利用SST 观测量无法估计探测器的绝对位置信息。 然而, 探测器在地月平动点轨道的运行轨迹唯一, 可以根据SST 观测量确定相对或绝对位置信息［85］。 由于平动点轨道的加速度场具有较强的不对称性, 引力场的模型精度将决定探测器的运行轨迹是否唯一［86］。

月球探测任务常采用“圆型限制性三体模型”作为基本的动力学模型。 事实上, 太阳引力和太阳光压是不可忽略的摄动源, 会影响地月系统和探测器的运动状态, 这些影响总结为以下方面:1）月球绕地球的运动不再是圆形, 轨道偏心率在1/23 ～1/15 之间周期性变化; 2）地球-月球系统的质心不再是惯性点, 而是绕太阳作椭圆运动; 3）月球绕地球运动的轨道面在惯性空间内变化, 其运动是周期性变化的章动和进动。 因此, “圆型限制性三体模型” 与平动点轨道的动力学环境存在较大差异。

目前的研究主要考虑了三个因素的影响: 月球轨道相对于黄道面的轨道倾角、 月球轨道进动和月球轨道偏心率。 针对地月三角平动点, 探测器采用四体动力学模型一定程度上改善了地月系统的模型精度, 但是没有消除月球轨道偏心率的影响。 针对地月共线平动点, 在假设月球轨道倾角为零、 太阳与月球作圆形运动的条件下, 探测器采用高精度限制性四体模型, 但无法克服白道面在惯性空间变化的问题。 Andreu 等［87］采用拟周期双圆模型找到了接近于真实力学环境的轨道初值, 但是该动力学模型的复杂度非常高, 难以在工程中应用。

因此, 建立高精度、 适合在轨计算的平动点轨道模型需要重点考虑月球轨道进动和月球轨道偏心率等因素的影响。

（2）有效的轨道保持策略

在地月空间中, LiAISON 方法利用平动点轨道的非对称性能够估计参与探测器的绝对位置信息。由于平动点轨道具有很强的不稳定性, 探测器很容易偏离标称轨道。 从给定初始状态开始, 探测器的动力学模型误差和观测噪声随着时间推移而增加, 大约1.6 天增加一倍。 因此, 探测器需要采用有效的轨道保持策略消除轨道偏离误差, 确保在标称轨道上稳定运行［88］。

目前, 深空探测器的轨道控制模式主要有两种: 瞬时喷气模式和连续小推力保持模式［89］。 在工程应用中, 由于脉冲机动技术发展成熟, 常采用瞬时喷气模式进行平动点轨道保持工作。 但是,脉冲机动工作原理决定了此模式只适用于间断的松散控制, 而无法进行持续、 高精度的轨道保持任务。 相比而言, 连续小推力保持模式具有连续提供推力、 可控性强的优点, 已成为更受青睐的轨道控制方案。 在平动点轨道保持任务中, 连续小推力保持模式通过对非线性系统进行线性化近似处理, 取得了一定的轨道保持效果, 但大幅值轨控效果不佳, 且存在控制精度低、 燃料消耗较大等问题。 为了能够直接处理非线性系统, 学者们提出了许多基于非线性模型的控制策略。 这些控制策略在一定程度上改善了轨道保持性能, 使得轨控精度更高, 燃料消耗更少。 但是, 非线性方法要求动力学模型的精度足够高, 且对系统不确定性等因素的鲁棒性较差。

因此, 为了改善平动点轨道的站位保持性能,需要克服非线性系统对精确建模的依赖, 控制系统的鲁棒性也有待加强。

4 结论与展望

综上所述, 国外已经多次成功应用天文测角导航技术, 并已经开始测试自主性更强、 精度更高的深空星间测量导航技术。 随着我国深空探测任务的快速发展, 结合月球和火星探测工程的爆发期, 需要突破深空自主导航的各项关键技术,并发展新型导航方法的在轨应用, 如星间测量导航、 天文脉冲星导航等方法, 为我国的深空探测任务提供自主导航技术支持。

为了使我国深空探测自主导航技术达到国际先进水平, 早日实现航天强国目标, 除了上文已提及的技术内容外, 还需要对以下方面进行深入研究:

（1）核推进方式下的高精度建模

2021 年, 美国DARPA 提出了核推进计划——DRACO, 以支持快速登月以及人类登陆火星任务。高比冲核推进将作为未来深空探测器的主要动力来源, 使深空探测任务所需的发射规模缩小数十倍。 核推进技术减少了深空探测器到月球、 火星等天体的飞行时间, 但是对于自主导航系统而言,高比冲核推进技术加大了建立高精度轨道动力学模型的难度。 因此, 对核推进探测器建立连续、准确的动力学模型是未来深空探测自主导航技术的重点研究方向。

（2）自主任务规划技术

现如今, 大部分探测器在执行深空探测任务之前先由地面专家规划好各种在轨活动, 然后通过上行链路传达控制指令。 这种预先规划任务的方法要求有足够的星地通信时间以及相对稳定的运行环境, 但是深空探测具有很大的不确定性且频繁进行星地交互的成本较高。 因此, 需要发展在线任务规划技术, 使探测器具备自主规划能力,以更好地应对深空中的突发状况。

（3）多导航信息源融合技术

由于深空环境复杂多变, 采用单一导航方法无法满足深空探测自主导航技术要求, 需要发展高精度、 高稳定性、 抗干扰能力强的组合导航系统。 例如, 惯性导航在实际应用中有很高的精度,但导航误差会随着时间的推移而增大, 通过其他导航系统提供准确的修正信息, 实现各种导航方法优势互补。 探测器在深空任务中会经历多个飞行阶段, 结合多种导航方法构成多信息源融合一体化导航系统, 是提高深空探测自主导航精度的有效手段之一。

（4）地面仿真技术

由于深空探测任务的代价巨大, 需要建立完善的地面仿真试验验证系统, 以验证探测器的在轨有效性、 可行性和实用性。 一方面, 要减小导航模拟器与真实导航目标源的环境参数差异, 保证地面卫星仿真技术的真实性; 另一方面, 导航系统规模逐渐扩大, 超大规模的计算需求日益增长, 有必要在半物理仿真中实现系统模型的自动分解和并行化计算。