“通性通法”是高考解题的康庄大道——以2022年高考试题为例看构造法解函数对称与周期问题

沈 涛

(陕西省宝鸡市石油中学)

2022年高考数学试卷的整体难度有所上升,从新课程标准里面以及高考改革的一些指导意见中,就能略见端倪,其中有这样的一些整体的提炼,“坚持通性通法的考查”“不回避课堂教学热点、重点知识、重点方法重点考查”“稳中有变、立足基础、突出能力、锐意求新”“多角度、多维度、多层次考查数学思维品质”“考查学生的数学素养和学习潜能”,那么,在今后的教学中,如何应对高考目前的要求,是值得我们深思的事情,我觉得还是“以不变应万变”为好,“不变”指的是数学本身的思维方法和基本的解题技能,这个是需要我们加强研究和学习,思维层次的提升和数学方法论指导的解题研究可以帮助我们更好地应对高考试题难度上升带来的困难局面.

构造法作为一种数学方法,不同于一般的逻辑方法,它属于非常规思维,其本质特征是“构造”,用构造法解题,并无一定的套路,表现出思维的试探性、不规则性和创造性.构造法解题是一种创造性思维活动,其关键是借助对问题特征的敏锐观察,展开丰富的联想,实施正确的转化.在解题中利用已知条件和数学知识,通过观察、联想,构造出满足条件的数学对象,或构造出一种新的问题形式,使问题的结论得以肯定或否定,使问题转化,有时更能使数学解题打破常规,另辟蹊径,巧妙地获得解决.构造法解题是数学核心素养的集中体现.

有相当多的数学命题是具有一般性质的数学问题的特殊体现,我们构造出这个一般性质,用来对问题进行判断或推证,是一种富有创造性的解题方法,这种解题思路关键是构造出符合题目要求的一般性规律性质.有时,我们也可以构造一个满足题目要求的特例,利用这个特例来解决问题.

以2022年高考数学新高考Ⅰ卷12题为例,解答这个题,有两种构造方法,一是构造符合题目要求的一般性质,利用性质解题;二是构造满足题目要求的特殊函数来解题.

1.根据此题目要求构造出的一些函数性质

性质1:函数y=f(x)的图象关于直线x=a对称⟺f(x)=f(2a-x)⟺f(a-x)=f(a+x).

推论:f(x+a)是偶函数⟺f(x+a)=f(-x+a)⟺y=f(x)的图象关于直线x=a对称.

性质2:函数y=f(x)的图象关于点(a,b)对称⟺f(a+x)+f(a-x)=2b⟺2b-f(x)=f(2a-x).

推论:f(x+a)是奇函数⟺f(-x+a)=-f(x+a),进而可得到y=f(x)的图象关于(a,0)中心对称.

性质3:f(x)+f(x+a)=k(k为常数),y=f(x)的周期T=2a.

证明:构造方程组,f(x)+f(x+a)=k,f(x+a)+f(x+2a)=k,两式相减可得f(x+2a)=f(x),f(x)的周期T=2a.

性质4:双对称出周期:若一个函数f(x)存在两个对称关系,则f(x)是一个周期函数.

(1)若函数f(x)的图象关于点(a,0),及点(b,0)对称,则函数f(x)是周期T=2|b-a|的周期函数.

证明:f(x)=-f(2a-x),f(x)=-f(2b-x)⟹f(2a-x)=f(2b-x)⟹T=2|b-a|.

(2)若函数f(x)的图象关于直线x=a及x=b对称,则函数f(x)是周期T=2|b-a|的周期函数.

证明:f(x)=f(2a-x),f(x)=f(2b-x)⟹f(2a-x)=f(2b-x)⟹T=2|b-a|.

(3)若函数f(x)的图象关于直线x=a对称,且关于点(b,0)对称,则函数f(x)是周期T=4|b-a|的周期函数.

证明:f(x)=f(2a-x),f(x)=-f(2b-x)⟹f(2a-x)=-f(2b-x)⟹f(x)=f(4b-4a+x).

性质5:已知函数f(x)及其导函数f′(x)的定义域为R.

(1)若f(x)的图象关于直线x=a对称⟹f′(x)的图象关于点(a,0)对称.

证明:若f(x)的图象关于直线x=a对称,则f(a+x)=f(a-x),则f′(a+x)=-f′(a-x),所以f′(x)的图象关于点(a,0)对称.

(2)若f(x)的图象关于点(a,b)对称⟹f′(x)的图象关于直线x=a对称.

证明:若f(x)的图象关于点(a,b)对称,则f(a+x)=2b-f(a-x),则f′(a+x)=f′(a-x),所以f′(x)的图象关于直线x=a对称.

推论1:若f(x)是奇函数,则导函数f′(x)是偶函数.

推论2:若f(x)是偶函数,则导函数f′(x)是奇函数.

性质6:已知函数f(x)及其导函数f′(x)的定义域为R,若函数f(x)是周期为T的周期函数,则其导函数f′(x)也是周期为T的周期函数.

证明:若f(x+T)=f(x),则f′(x+T)=f′(x).

2.构造方程组,将两个抽象函数f(x),g(x)看成二元,消元分别得到f(x),g(x)各自的代数关系

( )

A.-21 B.-22

C.-23 D.-24

【解析】方法一:构造方程组,结合性质,化同名函数,寻找同名函数间的关系

①-②得f(x)+f(-2-x)=-2 ③,

由性质2的推论知f(x)的图象关于点(-1,-1)中心对称.

所以g(2-x)=g(2+x),

两式相减可得f(x)+f(x-2)=-2 ④,

由性质3可知f(x)的周期T=4,

所以f(-x)=f(x),

所以f(x)为偶函数,

（三）建立单亲家庭学生档案并进行个案追踪。了解和掌握班级内单亲家庭子女人数，并熟悉掌握其家庭状况、单亲原因等，建立单亲家庭学生档案。学生工作者应加强对他们的学习、生活、心理、行为和家庭情况的了解、跟踪，并详加记录。同时把每个单亲家庭学生的教育责任到人，由班主任或任课教师或其他责任人负责其心理疏导、学习辅导、生活关照、行为矫正等，定期与家长联系，掌握单亲家庭学生在家中和社会上的情况。

此时也可由性质4得f(x)的周期T=4,

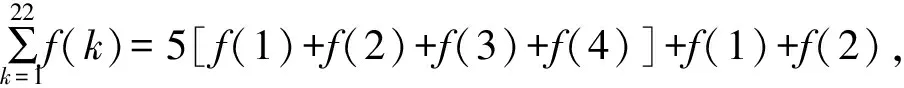
由④知f(1)+f(1-2)=-2,

f(3)=f(-1)=f(1)=-1.

由f(0)+g(2)=5,得f(0)=1.

由f(0)+f(2)=-2,

得f(2)=-3,f(4)=f(0)=1,

方法二:构造满足题目要求的特殊函数

由方法一知f(x)的图象关于点(-1,-1)中心对称,

f(-x)=f(x),f(x)的周期T=4,

可得f(1)=-1,f(2)=-3,

f(3)=-1,f(4)=1,

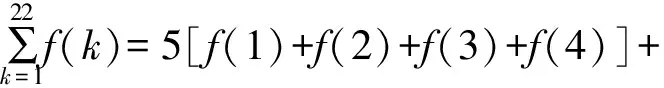
方法三:根据函数的性质求解

若y=g(x)的图象关于直线x=2对称,

则g(2-x)=g(2+x),

因为f(x)+g(2-x)=5,

所以f(-x)+g(2+x)=5,

故f(-x)=f(x),

则f(x)为偶函数.

由g(2)=4,f(0)+g(2)=5,

得f(0)=1.

由g(x)-f(x-4)=7,

得g(2-x)=f(-x-2)+7,

代入f(x)+g(2-x)=5,

得f(x)+f(-x-2)=-2,

则f(x)关于点(-1,-1)中心对称,

所以f(1)=f(-1)=-1.

由f(x)+f(-x-2)=-2,f(-x)=f(x),

得f(x)+f(x+2)=-2,

所以f(x+2)+f(x+4)=-2,

故f(x+4)=f(x),f(x)的周期为4,

所以f(4)=f(0)=1.

由f(0)+f(2)=-2,

得f(2)=-3.

又f(3)=f(-1)=f(1)=-1,

( )

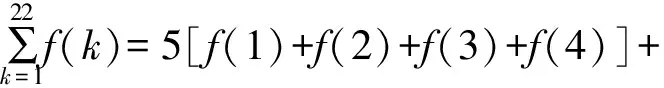
A.-3 B.-2

C.0 D.1

【解析】构造方程组,将二元变量变为一元变量,解法较为简单.

令y=1得f(x+1)+f(x-1)=f(x)·f(1),

则f(x+1)+f(x-1)=f(x),

则f(x+1)=f(x)-f(x-1),

两式相加得f(x+3)=-f(x),

故f(x)的周期为6.

令x=1,y=0得f(1)+f(1)=f(1)·f(0),

可得f(0)=2,

f(2)=f(1)-f(0)=1-2=-1,

f(3)=f(2)-f(1)=-1-1=-2,

f(4)=f(3)-f(2)=-2-(-1)=-1,

f(5)=f(4)-f(3)=-1-(-2)=1,

f(6)=f(5)-f(4)=1-(-1)=2,

3.构造满足题目条件的特例函数,利用特例函数展开研究

( )

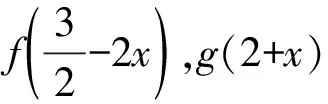
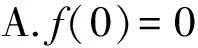
C.f(-1)=f(4) D.g(-1)=g(2)

【解析】方法一:构造满足题目要求的函数

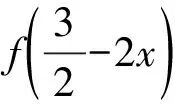
因为g(x)=f′(x),

且g(x)的图象关于直线x=2对称,

由性质5可知f(x)的图象关于点(2,b)中心对称,

据此构造函数f(x)=sinπx+b,x∈R,

则g(x)=f′(x)=πcosπx,

逐个检验选项,

可得B,C正确,故选BC.

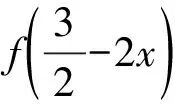
由g(2+x)为偶函数可知g(x)的图象关于直线x=2对称,

因为g(x)=f′(x),

且g(x)的图象关于直线x=2对称,

由性质5可知f(x)的图象关于点(2,b)中心对称,

综上,函数f(x)与g(x)均是周期为2的周期函数,

所以有f(0)=f(2)=b,

所以A错误;

f(-1)=f(1),f(4)=f(2),f(1)=f(2),

故f(-1)=f(4),

所以C正确;

所以B正确;

又g(1)+g(2)=0,

所以g(-1)+g(2)=0,

所以D错误,故选BC.

4.具有对称中心的函数的极值点关于对称中心对称

【例4】(2022·全国新高考Ⅰ卷·10)已知函数f(x)=x3-x+1,则

( )

A.f(x)有两个极值点

B.f(x)有三个零点

C.点(0,1)是曲线y=f(x)的对称中心

D.直线y=2x是曲线y=f(x)的切线

【解析】因为f(x)=x3-x+1,

所以f′(x)=3x2-1,

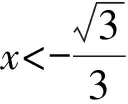
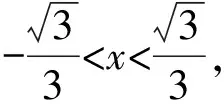
所以f(x)有两个极值点,

故A正确;

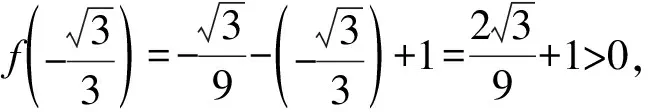
当x→-∞时,f(x)→-∞,

所以f(x)仅有一个零点,

故B错误;

又f(-x)=-x3+x+1,

则f(-x)+f(x)=2,

所以f(x)的图象关于(0,1)中心对称,

故C正确;

设切点P(x0,y0),

若y=2x是其切线,

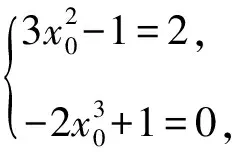
该方程组无解,

故D错误,故选AC.

5.抽象函数由奇偶性构造关系式

( )

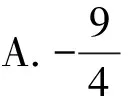
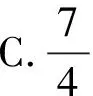
【解析】因为f(x+1)是奇函数,

由性质2得f(-x+1)=-f(x+1).

由性质2知f(x)的图象关于(1,0)对称,

又因为f(x+2)是偶函数,

所以f(x+2)=f(-x+2),

f(x)的图象关于直线x=2对称,

由性质4得函数f(x)的周期T=4|2-1|=4.

又f(1)=-f(1),

所以f(1)=0,f(0)=-f(2),f(3)=f(1),

即f(3)+f(0)=f(1)-f(2)=6,f(2)=-6,

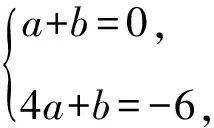
解得a=-2,b=2,

所以f(x)=-2x2+2.

又函数f(x)的周期T=4,

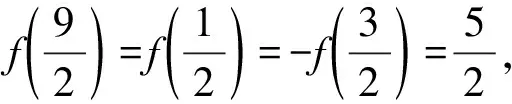
6.综述

在解决函数性质类问题的时候,我们通常可以借助一些二级结论,寻求解题的通性通法,进而达到简便计算的效果.

探寻高考试题的解题思路、通法、规律是每一个高中数学教师必做的功课,但是绝大多数师生仅仅埋头解题,陷于题海之中,往往因缺乏方法理论的学习研究而迷失正确的方向,为了改变这种状况,我们应从数学方法理论与解题的结合上入手,试图做到以数学方法理论指导解题探究,从而科学地提升解题能力,同时,通过解题研究更好地理解数学方法理论,两者相得益彰.

解数学问题时,常规的思考方法是由条件到结论的定向思考,但有些问题按照这样的思维方式来寻求解题途径确实比较困难,甚至无从着手,在这种情况下,经常要求我们改变思维方向,换一个角度思考,以找到一条绕过障碍的新途径,构造法就是这样的手段之一.我们所说的利用函数思想、方程思想解题具体体现就是构造函数、构造方程,实际上就是构造法的体现.