同构放缩联袂至 转化一步天地宽
——2022年全国卷中同构法、放缩法的应用
2023-04-15李露琦
张 怡 李露琦
(1.山东省滨州实验中学; 2.山东省滨州北海中学)
1 前言
在2022年高考数学全国卷中,有几道试题的命制格外亮眼.它们既考查了基础知识,又聚焦了数学核心素养,突出对关键能力的考查.随着越来越多的省份进入新高考模式中,广大高中一线教师有必要对高考试卷作深入的研究,明晰试题的命制背景,挖掘试题的育人价值.拓展学生的思维水平,提升师生的备考能力.本文以2022年新高考Ⅰ、Ⅱ卷,全国甲、乙理科卷的部分试题为例,展示同构法、放缩法的应用.
2 相关概念
2.1 同构法
将题目条件中的等式或不等式通过适当的整理变形,形成拥有相同结构的式子,然后利用这个结构式构造相应的函数,再利用函数的基本性质解决问题.
2.2 放缩法
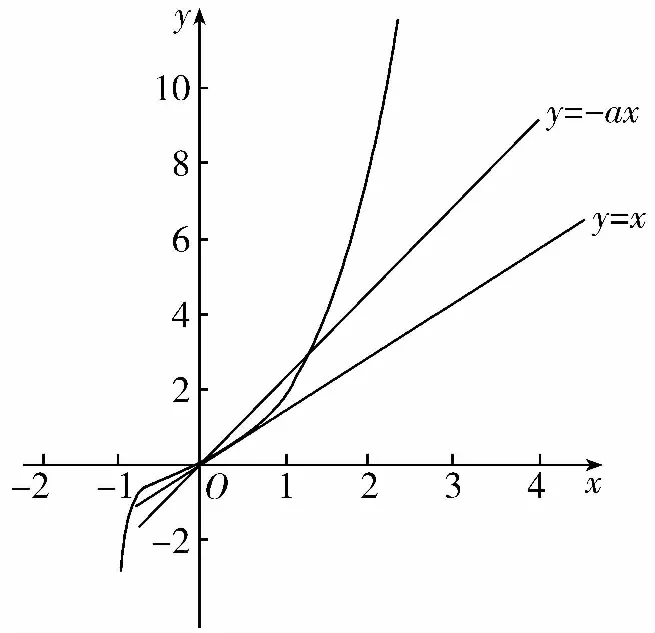
证明不等式A 在高考题目中经常出现的是将指数函数、对数函数放缩为幂函数的切线放缩法. 这样我们就得到了指数函数与对数函数的两个双边不等式: 以上关于指数函数、对数函数不等式的结论需要学生在理解关系的基础上熟记. 【思路探索】观察已知条件的结构,利用诱导公式将等式一侧的结构形式化成等式另一侧的结构形式,利用相同的结构构造对应的函数,再利用函数的单调性进行求解. 解:由题意得,f(x)的定义域是(0,+∞), 令x-lnx=t,x>0, 令t′=0,解得x=1. 所以当x∈(0,1)时,t′<0; 当x∈(1,+∞)时,t′>0, 所以t在(0,1)上单调递减, 在(1,+∞)上单调递增, 所以当x=1时,t取得最小值,且tmin=1, 即t≥1. 再令g(t)=et+t, 因为et在[1,+∞)上单调递增, t在[1,+∞)上单调递增, 则g(t)=et+t在[1,+∞)上单调递增, 所以g(t)min=g(1)=e+1, 所以f(t)min=f(1)=e+1-a≥0, 解得a≤e+1. 故a的取值范围为(-∞,e+1]. ( ) A.a C.c 【思路探索】观察题目中同时出现指数与对数的形式,因此考虑利用不等式放缩的方法,将指数、对数的形式化简至幂函数的形式,再进行比较.当放缩法无法比较大小时,作差后构造函数,转化为恒成立问题求解. 解:a,b的大小比较: 当且仅当x=0时等号成立, b,c的大小比较: 当且仅当x=1时等号成立. a,c的大小比较: a-c=0.1e0.1+ln(1-0.1), 令f(x)=xex+ln(1-x),x∈(0,0.1], 令k(x)=(1+x)(1-x)ex-1, 所以k′(x)=(1-x2-2x)ex>0, 所以k(x)>k(0)=0,所以f′(x)>0, 则f(x)在(0,0.1]上单调递增, 所以f(0.1)>f(0)=0, 所以a-c>0,即a>c. 综上,c 【例4】(2022·全国乙卷理·21节选)已知函数f(x)=ln(1+x)+axe-x.若f(x)在区间(-1,0),(0,+∞)各恰有一个零点,求a的取值范围. 【思路探索】将函数零点问题转化成两个函数的交点问题,再利用导数研究函数单调性的过程中,通过不等式放缩简化计算. 解:由题意得,f(x)=ln(1+x)+axe-x=0, 所以-ax=exln(1+x). 令g(x)=exln(1+x),x>-1, g(x)在(0,0)处的切线斜率k=g′(0)=1. 所以g(x)在(-1,0),(0,+∞)上单调递增, 当x→-1时,g(x)→-∞, 当x→+∞时,g(x)→+∞. 作出g(x)的大致图象如图所示, 当-a>1时,函数y=-ax与g(x)的图象在(-1,0),(0,+∞)上各有一个交点,即函数f(x)在(-1,0),(0,+∞)各恰有一个零点, 故a<-1. 【例5】(2022·全国新高考Ⅱ卷·22节选)已知函数f(x)=xeax-ex.当x>0,f(x)<-1,求a的取值范围. 【思路探索】待求的参数a在指数的位置上,考虑利用不等式放缩,将指数函数形式化简为一次函数形式,进而求解. 解:令g(x)=f(x)+1, 则g(x)=xeax-ex+1,x>0, 易知g(0)=0. 要证g(x)<0, 即证g(x) 即证g′(x)≤0, 即g′(x)=(1+ax)eax-ex≤0, 即eln(ax+1)+ax≤ex, 即ln(ax+1)+ax≤x. 得ln(ax+1)+ax≤(ax+1)-1+ax≤x, 所以2ax-x≤0, 即(2a-1)x≤0. (注:本解法来自滨州苍龙湖实验学校高三(3)班 任景豪) 【结语】总而言之,高中在学习函数后,需要将表面上不近相同的问题有机地衔接在一起,整合成自己的资源库,形成自己的解题特色.本文介绍的同构法源于指数恒等式alogaN=N,放缩法源于课后练习题,这些内容均是课本中基本的数学知识,学生也知晓,但他们找不到基本知识与高考题目之间的内在关系,这就需要教师发挥其主导作用,当学生的思维水平提升不上去时,教师应帮助学生建构完整的知识体系,帮助学生将这些知识整合并系统化. 同构法与放缩法在处理函数相关问题时可以大大节省计算时间,也能较好的考查学生对函数的综合应用能力.建议教师对这部分相关内容进行系统的讲解,引领学生对所掌握的数学知识和方法进行重构,通过有难度、有深度的试题激发学生的解题能力.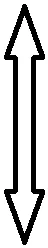




3 试题呈现
3.1 基于同构法的解答
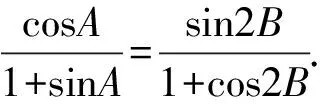

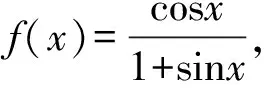
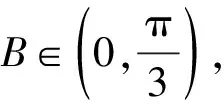






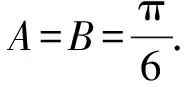

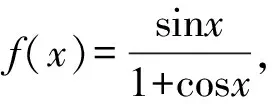
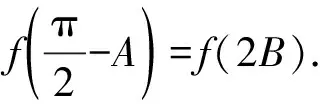

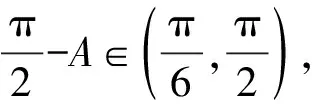



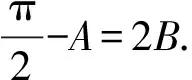


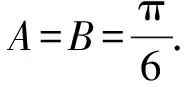
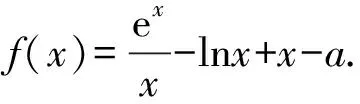


3.2 基于放缩法的解答
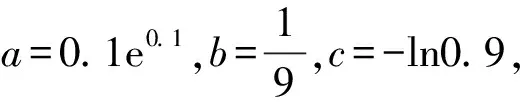



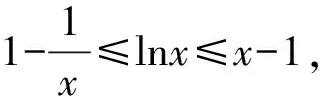






3.3 基于同构法放缩法综合应用的解答