注重变式探究 探索三新考向——以2022年八省八校联考第20题为例

王玉佩 张 超

(安徽省利辛县第一中学)

圆锥曲线中的存在与探索性问题能较全面地考查考生的数学运算和逻辑推理等数学核心素养,备受命题者的青睐.因为高中数学课堂内容多,时间紧,因此数学教师对存在性问题的变式研究比较少,所以学生们在考试中遇到这类题目的时候,往往会有无从下手的感觉.基于此本文以2022年八省八校联考(T8联考)第20题为例对圆锥曲线中存在性问题进行了变式探究,通过实例分析,了解变式探究在培养学生核心素养中的作用,分析变式探究在日常教学中的应用情况,认识变式探究对分析问题、解决问题的价值和意义,旨在提升学生的创新能力,探索三新考向.

一、实例分析变式探究

下面以2022年八省八校联考(T8联考)第20题为例,引导学生通过改变题目的条件或结论等方式对新的结论进行探究,探索试题的本质,提升考生的数学运算和逻辑推理核心素养.下面分别从存在问题中角度型、向量型、面积型、直线型等类型加以探析.

【母题】(2022·八省八校联考(T8联考)·20)

(Ⅰ)求椭圆E的方程;

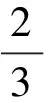
【试题分析】

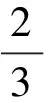
考查能力:数学运算核心素养,化归与转化、数形结合等思想.

思维引导:(1)根据椭圆的离心率及圆的几何性质求出a,b,即可求解.

(2)首先设直线方程,然后利用韦达定理求解即可.注意验证Δ>0.

【解析】

设点F1,F2关于直线l的对称点分别为M,N,由对称性易知,线段MN为圆C的一条直径,

所以|F1F2|=|MN|=2,即2c=2,即c=1,

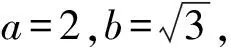
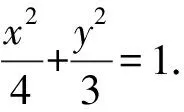
(Ⅱ)不存在.理由如下:因为原点O为线段F1F2的中点,圆心C为线段MN的中点,直线l为线段OC的垂直平分线,所以点O与C也关于直线l对称,

因为点C(2m,4m),

又直线l为线段OC的垂直平分线,

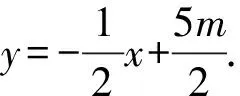
不妨设A(x1,y1),B(x2,y2),

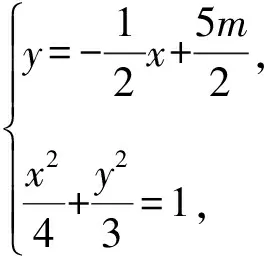
整理得4x2-10mx+25m2-12=0.

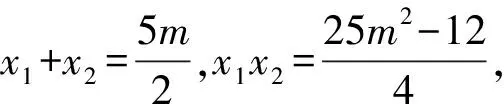
且Δ=100m2-16(25m2-12)>0,

所以kAC+kBC

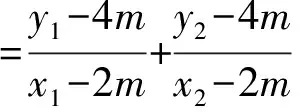
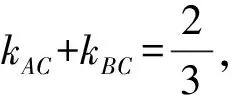
得2x1x2-m(x1+x2)-4m2=0,

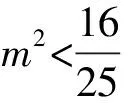
【评注】此题第(Ⅰ)问入口较难,对考生数学核心素养要求较高.通过第(Ⅰ)问也提醒我们教学中不能形成思维定势,教学中要注重提升学生的发散思维和创新力,以便应对反套路的陌生试题.

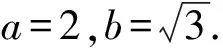
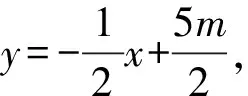
该问有部分学生容易忽略判别式Δ>0验证所计算的结果,最终容易导致误判.

【变式思路】该题第(Ⅰ)问非常灵活,符合“新课程,新教材,新高考”的新要,该试题源于教材又高于教材且能有效起到试题选拔功能.

第(Ⅱ)问则主要考查学生运算水平,解题方法相对比较单一,不能很好体现“三新”要求的既要重计算,又要重思维的选拔理念.所以笔者就想能不能设置一个问题兼顾计算、思维的训练.基于此本文从不同角度对试题进行变式探究.

【变式意义】变式后的问题力求能实现一题多解,同时兼顾计算、思维训练.从而实现试题改编后对不同层次考生都有选拔的目的,同时通过变式研究提升学生的创新能力.

基于此,下面笔者尝试从不同角度对试题进行变式研究.

【变式1】(知识变式)存在性问题之双曲线型

(Ⅰ)求双曲线E的方程;

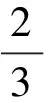
【解析】

设点F1,F2关于直线l的对称点分别为M,N,易知线段MN为圆C的一条直径,

所以|F1F2|=|MN|=4,即2c=4,即c=2.

于是a2=b2=2,

(Ⅱ)不存在.理由如下:因为原点O为线段F1F2的中点,圆心C为线段MN的中点,直线l为线段OC的垂直平分线,

所以点O与C也关于直线l对称,

因为点C(2m,4m),直线l为线段OC的垂直平分线,

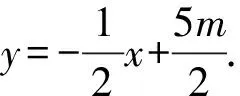
不妨设A(x1,y1),B(x2,y2),

整理得3x2+10mx-25m2-8=0,

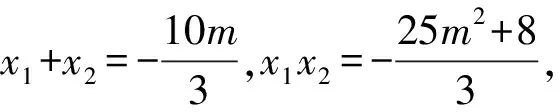
且Δ=100m2-12(-25m2-8)>0恒成立,

所以kAC+kBC

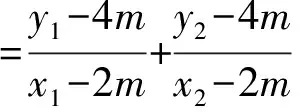
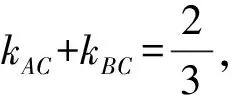
得2x1x2-m(x1+x2)-4m2=0,

即52m2=-16无解,

【评注】变式1从直线、椭圆问题变成直线、双曲线问题,两种题型不同视角切入,回归一般性,得出以上关系式中参数的常值情况,可以得到以下一般性结论.该变式关键点是培养学生一题多解,多题一解的解题能力.

【变式2】(素养变式)存在性问题之角度型

【解题思路】

即AC⊥BC,得kACkBC=-1.

【变式3】(素养变式)存在性问题之面积型

将(Ⅱ)中条件变为“设直线l与椭圆E相交于A,B两点,问:是否存在实数m,使S四边形AF2BC=2S△ABC?若存在,求出实数m的值;若不存在,说明理由.”

【解题思路】

方法1:由S四边形AF2BC=2S△ABC,得S△AF2B=S△ABC,

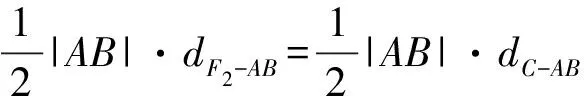
则只要dF2-AB=dC-AB即可.

又因为直线l:x+2y-5m=0,F2(1,0),

【评注】变式3的关键点:考生通过分析,由S四边形AF2BC=2S△ABC等价转化成dF2-AB=dC-AB.显然该题通过方法2直接求解难度较大.

【变式4】(知识变式)存在性问题之向量型

【解题思路】

设A(x1,y1),B(x2,y2),

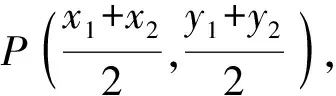
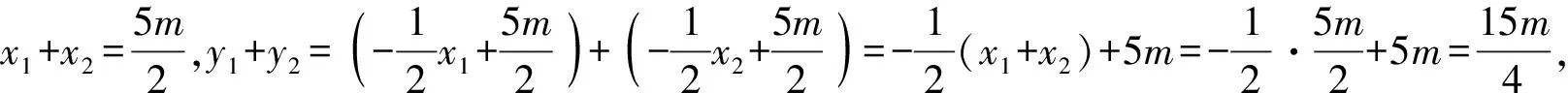
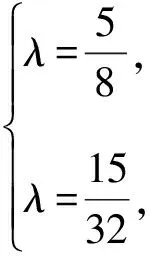
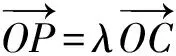
解法二:上同解法一,

易知点O,C,P共线,则只要kOC=kOP即可.

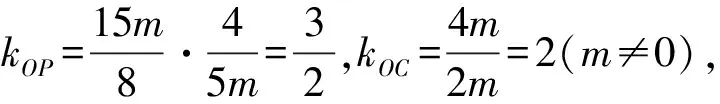
因为kOP≠kOC,

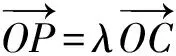
【评注】该变式把以斜率知识为背景变成以向量共线知识为背景,变式后的题目解法更灵活,解题思路更加清晰.通过此变式在教学中还能引导学生归纳求解字母参数值的存在性问题的解题策略:①假设→②推理与计算→若不出现矛盾,就说明满足条件的参数值存在;若出现了矛盾,则说明满足条件的参数值不存在.该变式关键点是利用韦达定理求中点P的坐标.

【变式5】(素养变式)存在性问题之定直线型

将(Ⅱ)中条件变为“设直线l与椭圆E相交于A,B两点,弦AB的中点为M,直线OM与椭圆E相交于F,D两点,问:是否存在直线l,使得|AM|2=|FM|·|DM|成立?若存在,求直线l的方程;若不存在,说明理由.”

【解析】

假设存在直线l,使得|AM|2=|FM|·|DM|成立,

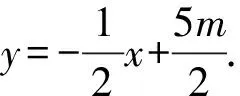
设A(x1,y1),B(x2,y2),

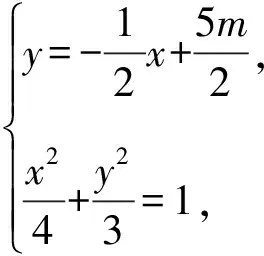
整理得4x2-10mx+25m2-12=0,

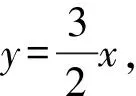
解得x2=1,

因为|AM|2=|FM|·|DM|

=(|OF|-|OM|)(|OD|+|OM|),

且|OF|=|OD|

所以|AM|2=|OF|2-|OM|2,

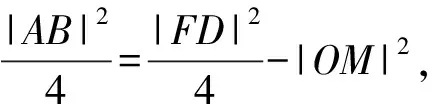
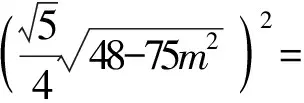
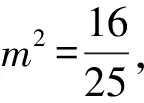
所以直线l的方程为x+2y+4=0或x+2y-4=0.

【评注】本题(Ⅱ)问的核心在于转化|FM|·|DM|中弦长的关系,

由|FM|=|OF|-|OM|,

|DM|=|OD|-|OM|,

且|OF|=|OD|,得|AM|2=|OF|2-|OM|2.

因此|AB|2=|FD|2-4|OM|2,

转化为弦长|AB|,|FD|,|OM|三者之间的数量关系,易计算.

此变式目的是提升学生数学抽象、逻辑推理、数学运算等综合素养.

二、存在性及探究性问题解题策略及三新考向思考

通过2022八省八校联考20(T8联考)试题分析及变式研究,结合实际教学,本人得到如下启示:

1.圆锥曲线中存在性问题解题策略

变式探究的意义在于“解一题,会一类,通一片”,即通过研究典型试题的背景、知识、解题方法、变形延伸等,而后从中归纳总结出相似问题的解决思路和解题策略.通过变式研究不难发现存在性问题解题可通过:四个步骤,三个注意的解题策略.

步骤1:设(设点、直线)

注意①:直线斜率存在性分析、直线形式分析.

步骤2:联(联立→消元→韦达定理)

注意②:在求范围、值时,注意判别式Δ检验结果.

步骤3:列(列(不)等式→消元)

注意③:注意列式可通过:中点型、弦长型、向量型、斜率型、目标函数型、平面几何性质型、常见结论型等.

步骤3:求(求值、取值范围、定值或定点、方程、存在性探究问题)

通过引导学生归纳解题思路,思考变式试题解题策略.提升学生“解一题,会一类,通一片”的综合素养.

2.圆锥曲线中存在性问题新高考命题动向

从近两年新高考及模考试题研究中发现,圆锥曲线中存在与探索性问题主要变化是:背景新颖化;题型多样化;信息增量化;计算、思维兼顾化;强化数学运算、逻辑推理、直观想象等数学核心素养的考查.

(1)背景新颖化

通过创设新颖的试题情境,创新试题呈现方式,考查学生们的阅读理解能力,体现思维的灵活度,考查学生们的数学抽象与逻辑推理等核心素养.

(2)题型多样化

在“三新”背景下圆锥曲线中存在性探究问题必将是新高考命题的热点,探索存在性常考题型:数量关系型、向量型、几何关系型、角度型等.同时由于导函数的介入,切线问题也常常被引入到综合性的问题中.

(3)信息增量化

圆锥曲线中存在性试题在试卷中难度有增加的趋势,其目的不仅要对圆锥曲线的基本概念、方法、技能方面进行考查,还要对思维方面进行考查.所以存在性试题的命制既要重视计算,又要兼顾思维.像2022八省八校联考(T8联考)第20题第(Ⅰ)问信息量增加、方式更为灵活.

(4)计算、思维兼顾化

圆锥曲线存在性问题需要熟练掌握圆锥曲线的基本知识和基本技能,所以我们在教学中要重视计算经验积累,同时也要将试题合理的变式,提升发散思维的能力.