例谈三角函数专题突破的聚焦点

张建明 祝 峰

(1.安徽省淮北市教育科学研究所; 2.安徽省濉溪县第二中学)

依据《普通高中数学课程标准(2017年版2020年修订)》(以下简称《课标》)命制的新高考试题,强化了考试与教学的衔接,对中学数学教学依标施教有着积极正向的引导作用.在明确《课标》对三角函数专题内容和水平要求的基础之上,结合实例,提出四个三角函数专题突破的聚焦点,分别为聚焦“四基”,查缺补漏、构建网络;聚焦知识生成过程,揭示本质、深化理解;聚焦“关键能力”,纲举目张、以简驭繁;聚焦“一般观念”,训练思维、发展素养.旨在提升“三新”背景下高考备考教学的针对性及有效性.

1 聚焦“四基”,查缺补漏、构建网络

为贯彻《深化新时代教育评价改革总体方案》要求,数学高考会不断强化“基础性”的考查,要求学生在深刻理解基本概念和基本思想方法的前提下,自主把握知识之间的内在联系,深度揭示数学问题的本质,因此高中教学要在培养学生的基础知识、基本技能和思想,以及基本活动经验上下功夫.高考备考教学不应沦为“归题型”“刷套路”模式,应借助典型的高考试题,准确定位学生基础知识、基本技能、基本思想上的薄弱点,在发现问题、提出问题、分析问题、解决问题的过程中,丰富学生的基本活动经验.在查缺补漏、构建网络的教学中,帮助学生强化知识理解的深刻性,提升方法、思想应用的自觉性、灵活性和创造性.

( )

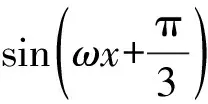
(2)是一类什么问题?三角函数图象、性质的应用问题.

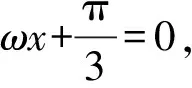
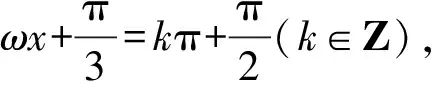
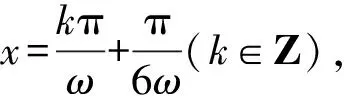
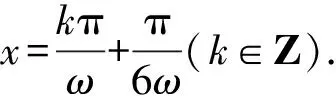
因为ω>0,f(x)在(0,π)上恰有三个极值点,

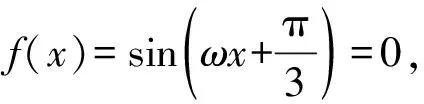
又f(x)在(0,π)上恰有两个零点,

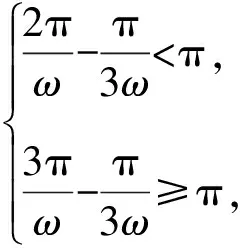
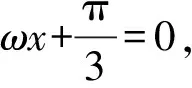
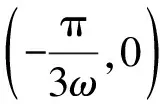
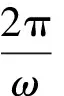
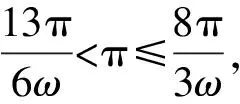
2 聚焦知识生成过程,揭示本质、深化理解

只有学生亲历知识生成过程,才能深刻理解知识发生的背景、意义和本质,若经历不够充分,那么后续学习和应用知识就会出现大麻烦,但这在数学高考备考的课堂教学中并没有引起教师的足够重视,很多教师认为知识生成过程是新授课要解决的问题,过程中没有什么题目可以让学生做,没什么可教,往往采用“一个定义,三项注意”的“告诉式”备考复习.殊不知,有些核心概念和原理,新授课时学生对其产生过程的经历就不够充分,加之当时认知水平的限制,学生对知识发生的真正原因,发生过程中蕴含的思维方法,以及知识背后数学思想的认识,不一定能一次性到位.因此在日后的能力立意、素养导向、综合性较强的实际问题应用中就会无所适从.建议教师在高考备考过程中,应结合典型高考试题求解时出现的错解,带领学生再次经历相关核心概念和原理的生成过程,进一步揭示本质,深化认识.

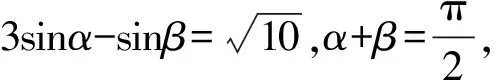
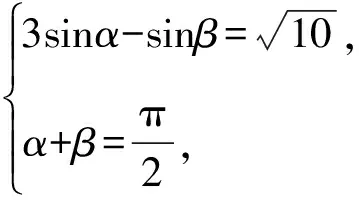
由辅助角公式得

即sin(α+φ)=1,

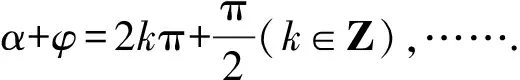
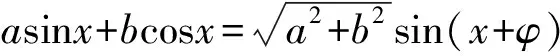
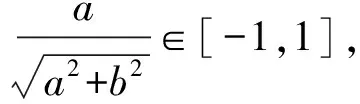
高考备考教学不同于新授课教学,教学中应帮助学生增加知识理解的深度和广度,拓宽方法和思想的联系性和灵活性.想要学生真正掌握数学知识,靠掐头去尾烧中段、大量的解题训练是做不到的,必须让学生亲历获得研究对象及应用数学知识解决问题的完整过程.

3 聚焦“关键能力”,纲举目张、以简驭繁

我们可以从多种视角看待高考试题,借助其设计出不同的高考备考教学,这与教育理念、教学目标、教学思维有着密切关系.如果仅就题论题,必将在浩如烟海的数学试题中迷失方向.如果从知识和技能视角看试题,能将无限题海转化为有限多的知识和技能,但面对能力立意、素养导向的新高考,常无法有效调动和运用所掌握的知识和技能.如果从数学思维和关键能力视角看试题,就能找到牵一发而动全身的“纲”.纲举才能目张,抓住了题目的“纲”,才能抓住解题的关键,与其盲目“刷题”、机械“套路”,不如把握试题的本质要素,从数学思维和关键能力视角剖析试题,以培养学生数学关键能力为基点,以简驭繁,这既是有效提升考试成绩的“大道”,也是利于学生素养发展的“王道”.

( )

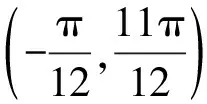
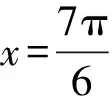
②这是一类什么问题?三角函数图象和性质应用、导数几何意义的问题.

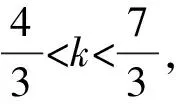
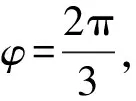
作出函数f(x)的大致图象,如图所示.

故A正确;

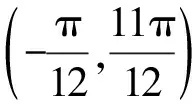
故B错误;

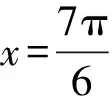
故C错误;

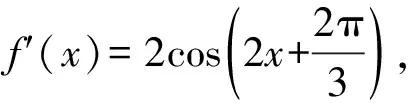
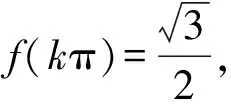
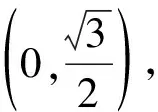
故D正确,故选D.

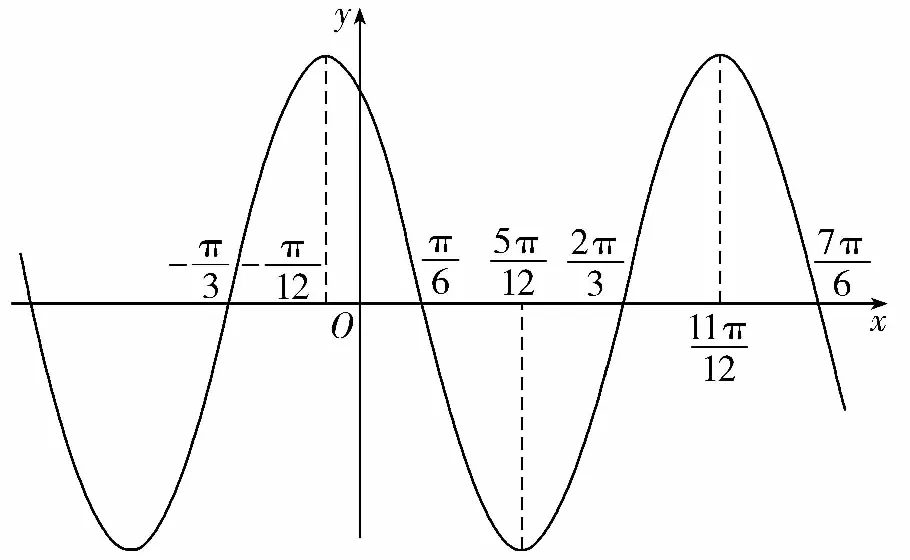
(2)数学运算能力.体现在两个方面,一是借助对称中心,获得φ的表达式,进而结合其取值范围,确定φ的值.通过推理求得函数的单调区间、图象对称轴、极值点,并检验相关选项的正确性;二是借助导数的几何意义和导数运算,获得函数图象切线,验证选项D的正确性.在问题解决过程中,对考生的运算习惯、运算规范化、条理性,以及面对复杂运算时的心态等都是很大的考验.

(3)逻辑推理能力.体现在解题思路形成时基于经验与直觉的合情推理过程,以及思路可行性、有效性在演绎推理中的检验过程.

4 聚焦“一般观念”,训练思维、发展素养

《课标》指出,高中数学教育能够帮助学生掌握现代生活和进一步学习所必须的数学知识、技能、思想和方法,提升学生的数学素养,并最终达成“三会”(会用数学的眼光观察世界、会用数学的思维思考世界、会用数学的语言表达世界)目标.“三会”是数学核心素养的灵魂,更是新高考数学命题的立意点,它体现在学科一般观念之中.学科一般观念泛指对相关知识学习和研究具有广泛、持久、深刻影响的基本数学思想方法和基本思维策略方法,在数学问题解决中具有统摄性、一般性、普适性的作用.在高考备考教学中,应通过对典型高考试题的探究,感悟试题创新的命制方式,凝练学科一般观念,助力学生在掌握“四基”,提升“四能”的基础上,有效发展学科核心素养.

【例4】(2022·全国乙卷理·17)记△ABC内角A,B,C的对边分别为a,b,c,已知sinCsin(A-B)=sinBsin(C-A).

(Ⅰ)证明:2a2=b2+c2;

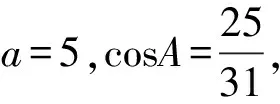
行文需要,下文仅以第Ⅰ问为例说明问题.

【分析】(1)已知什么?要证什么?已知三角形中三个角之间的关系sinCsin(A-B)=sinBsin(C-A),证明三边关系2a2=b2+c2成立.

(2)这是一类什么问题?三角形中的边角互化问题.

(3)问题解决的基本思路是什么?三角形中边角互化常依据大边对大角、正弦定理、余弦定理展开.

【证明】证法一:边角互化

因为sinCsin(A-B)=sinBsin(C-A),

所以sinCsinAcosB-sinCcosAsinB=sinBsinCcosA-sinBcosCsinA,

由正弦定理得accosB-bccosA=bccosA-abcosC,

【一般观念分析】已知角的关系探讨边的关系是问题的本质.三角形中基本的边角关系有正弦定理、余弦定理,三角形中边角关系的转化是这些定理背后的基本策略.教学中应通过实例,呈现这些定理的发生、构建和应用过程,让学生感受到“边角互化”是这些定理蕴含的学科一般观念.

证法二:化归与转化

因为sinCsin(A-B)=sinBsin(C-A),

所以由三角形内角和定理及诱导公式得

sin(A+B)sin(A-B)=sin(C+A)sin(C-A),

由两角和差的正弦公式得

sin2Acos2B-cos2Asin2B=sin2Ccos2A-cos2Csin2A.

由同角三角函数的基本关系得

sin2A(1-sin2B)-cos2Asin2B=sin2C(1-sin2A)-cos2Csin2A,

即sin2A-sin2Asin2B-cos2Asin2B=sin2C-sin2Csin2A-cos2Csin2A,

即sin2A-sin2B(sin2A+cos2A)=sin2C-sin2A(sin2C+cos2C),

整理得2sin2A=sin2B+sin2C,

由正弦定理得2a2=b2+c2.

【一般观念分析】知识方面,三角形内角和定理学生特别熟悉,但三角形问题解决过程中容易被忽视,它是三角形中三个角之间建立联系的有效途径.和差角公式、诱导公式、同角三角函数的基本关系式等三角恒等式,则是角之间关系转化的必备公式.

学科一般观念方面,由2sin2A=sin2B+sin2C,结合正弦定理得2a2=b2+c2的过程,体现了“边角互化”的学科一般观念.由sinCsin(A-B)=sinBsin(C-A),结合三角形内角和定理和诱导公式得sin(A+B)sin(A-B)=sin(C+A)sin(C-A);由sin2Acos2B-cos2Asin2B=sin2Ccos2A-cos2Csin2A,进而由同角三角函数的基本关系得sin2A(1-sin2B)-cos2Asin2B=sin2C(1-sin2A)-cos2Csin2A,再转化为sin2A-sin2Asin2B-cos2Asin2B=sin2C-sin2Csin2A-cos2Csin2A,即sin2A-sin2B(sin2A+cos2A)=sin2C-sin2A(sin2C+cos2C),最终得2sin2A=sin2B+sin2C的系列过程中,体现了代数式结构、角的名称、函数名称逐步转换统一的过程.“化归与转化”观念,是在错综复杂的问题情境中,探索思路、寻求方法、准确推理、获得结论的重要学科一般观念.高考复习备考课堂教学中,有必要让学生在具体的问题求解实践中,感悟“化归与转化”观念的强大功能.

证法三:联系观

因为sinCsin(A-B)=sinBsin(C-A),

所以由三角形内角和定理及诱导公式得

sin(A+B)sin(A-B)=sin(C+A)sin(C-A),

由积化和差公式得

即cos2B+cos2C=2cos2A,

由余弦的二倍角公式得

1-2sin2B+1-2sin2C=2(1-2sin2A),

即2sin2A=sin2B+sin2C,

由正弦定理得2a2=b2+c2.

【一般观念分析】知识技能方面,“和差化积”与“积化和差”公式常被教师们认为“无需掌握”,笔者认为它们本质上是“和差角”公式的外延部分,从对知识深度理解视角看,有必要让学生在实际问题解决过程中体会其功能.实际上,《课标》明确要求学生能够推导出两组公式,但不要求记忆,2019年版北师大教材中,单列出一节来讲述这部分内容.

学科观念方面,由和差角公式联想到积化和差公式,是公式学习的一种常用策略,即“联系观”.大量的三角恒等变换公式,关系错综,形式灵活,如何能在这些杂乱无章的事物中厘清头绪,发现规律,搞清公式之间上下的逻辑关联,用联系视角理解知识,才能把握知识的内涵、外延以及其背后蕴含的思想和方法.

证法四:分类整合观

在△ABC中,

sinCsin(A-B)=sinBsin(C-A),

且sinC≠0,sinB≠0.

①若sin(A-B)=0,则sin(C-A)=0,

则A=B且C=A,

即A=B=C,

所以a=b=c,此时2a2=b2+c2成立.

②若sin(A-B)≠0时,

则sin(C-A)≠0,

由sinCsin(A-B)=sinBsin(C-A),

由两角差的正弦公式得

由正弦定理得

整理得2bccosA=a(ccosB+bcosC),

由余弦定理的推论得

即b2+c2-a2=a2,故2a2=b2+c2成立.

综上,2a2=b2+c2成立.

【一般观念分析】三角形中的三角函数除具有一般三角函数的全部性质外,又具有特殊性,sinC≠0且sinB≠0正是基于三角形的特征获得,要适时让学生认清“特殊”和“一般”的关系.代数式sinCsin(A-B)=sinBsin(C-A)两边均有差角和单角,在“整体观”统领下,把差角结构分别转化到等式一边,涉及到sin(A-B)是否为零的问题.先分类后整合的思维方法自然出现,这种证法看似冗杂,且最后又回到正、余弦定理的应用上,但学生在实际探究中,常会出现这样的想法,教学应鼓励学生从多角度思考问题,方法的多样性能够增加学生对问题认识的深刻性,更能有效增强学生思维的灵活性.