重过程,促反思:“二元一次方程”的教学案例
2023-04-15江苏省如皋初级中学
江苏省如皋初级中学
陆智红
数学教学的过程教育是关注学生体会知识的发生过程,在探究学习的过程中积累活动经验,学会思考的方法,提升综合素质.因此,数学教学不仅要关注结果,更要兼顾过程.过程教育是激发学生学习兴趣的动力,通过过程学习才能形成全面的认识,真正让学习发生.在日常教学中普遍存在过程教育不够充分,匆匆忙忙展示结果的现象,导致学生的认识不全面,学生的知识迁移能力弱等问题.笔者在教学中也在不断思考和实践过程教育,经过不断的反思和实践,初步形成了一点自己的认识.本文以“二元一次方程”为例,与大家分享本课的教学设计,供大家讨论交流.
1 教学实录
环节1:发现和提出问题的过程——明确研究对象.
师:我们学习过一元一次方程的应用,同学们学会了在实际问题中应用一元一次方程解决问题,那么我们还能从实际的生活问题中抽象出其他的应用形式吗?大家思考并讨论下面的问题1.
问题1小明要到邮局寄信,一共需要3元8角的邮费,小明现在有一些面额是6角和8角的邮票,请问他用这两种邮票,一共需要多少张才能凑够邮资?
师:首先这个问题我们需要解决几个未知量?你能从中找到几个等量关系?
生1:需要解决面额是6角和面额是8角的邮票张数这两个未知量,其中有一个等量关系,面额为6角的邮票张数乘0.6与面额为8角的邮票张数乘0.8的和为3.8元.
师:很好,我们找到了等量关系,那么能否根据这个等量关系列出我们所熟悉的一元一次方程呢?
生2:有两个未知数,不能列出一元一次方程.
师:如果将面额为6角和面额为8角的邮票的张数分别设为x与y,那么可以列出一个什么样的方程呢?
生3:0.6x+0.8y=3.8.
师:正确.这说明我们从这个生活问题中构建了含有两个未知数的方程.事实上,这样的情景还有许多,如,根据课本的前言内容能列出方程2x+1.2y=10.8;还有方程2a=3b+20也在很多生活场景中可以使用.
师:看来一元一次方程不能应用的场景中,含有两个未知数的方程也有非常广泛的用途.那么就需要我们去研究这样的方程有什么特征?在什么样的场景下可以使用?该如何求解呢?这节课我们就要来研究这些问题(揭示问题).
环节2:认识二元一次方程的特征活动——形成二元一次方程的概念.
师:请问方程0.6x+0.8y=3.8有哪些特点?
生4:这个方程有两个特点.第一,有两个未知数;第二,含有未知数的项的次数都为1.
生5:这个方程左右两边都是整式.
师:很好!那么方程2x+1.2y=10.8是否具备这样的特点?还有方程2a=3b+20呢?
生6:它们都具备这几个特点.
师:好的,那么我们给这样的方程下一个定义——含有两个未知数,并且含有未知数的项的次数都为1的方程叫做二元一次方程.就像0.6x+0.8y=3.8,2x+1.2y=10.8,2a=3b+20这些方程一样.


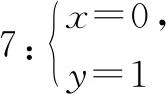
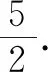
师:很好!那么一元一次方程和二元一次方程的解有什么区别呢?
生9:一元一次方程只有一个未知数,所以解也是一个数;二元一次方程含有两个未知数,所以解也是一对,而且不唯一.
师:观察得很仔细.方程的形式变了,方程的解以及个数自然也发生了变化.
环节3:探索解方程的过程——形成解二元一次方程的思想.
师:怎样解二元一次方程0.6x+0.8y=3.8?如果把x当成已知数,把该方程看作一元一次方程,可以求y这个未知数吗?
生10:可以.
师:那反过来,把y当成已知数,可以求解x这个未知数吗?
生10:当y是已知数时,这就变成了关于x的一元一次方程,所以可以求x的值.
师:很好.那么根据方程0.6x+0.8y=3.8,请尝试完成以下习题.
(1)用含有x的代数式表示y;
(2)当x分别为0,1,2,3,4,5,6时,请求出相应y的值;
(3)写出方程0.6x+0.8y=3.8的七个解.
学生思考答题.
师:哪位同学来回答第(1)问?

师:第(2)问哪位同学来接着回答?

师:好,第(3)问谁来?
师:好的,那么方程0.6x+0.8y=3.8一共有多少个解呢?
生14:有无数个解.
师:其中有几个解是符合问题1的条件?
师:这样,一开始的问题就解决了.一共需要面额为6角和8角的邮票分别为1张和4张,或者5张和1张.
在方程0.6x+0.8y=3.8中,能不能用含有y的代数式来表示x呢?应该如何求解?
生16:计算的方法和刚才是一样的.
师:那么我们回顾一下,解二元一次方程0.6x+0.8y=3.8一共有哪几个步骤?
生17:先将要求的未知数用含有另一未知数的代数式表示出来,接着由一个未知数的值求出另一个未知数相应的值,最后写出方程的解.
师:很好.那能不能归纳出一个普遍适用的解二元一次方程的步骤?
生18:一共三个步骤.第一步,表示出含有未知数的代数式;第二步,求出两个未知数相对应的值;第三步,写出方程的解.
师:总结得很好.其实解方程时采用了化归思想,也就是将二元一次方程化为一元一次方程,用三个字概括求解过程也就是解、代、写.
环节4:参与反思提升的活动——总结研究内容和方法.
(1)教师通过思维导图(如图1)的方式将本课的研究方法进行了图示和总结.
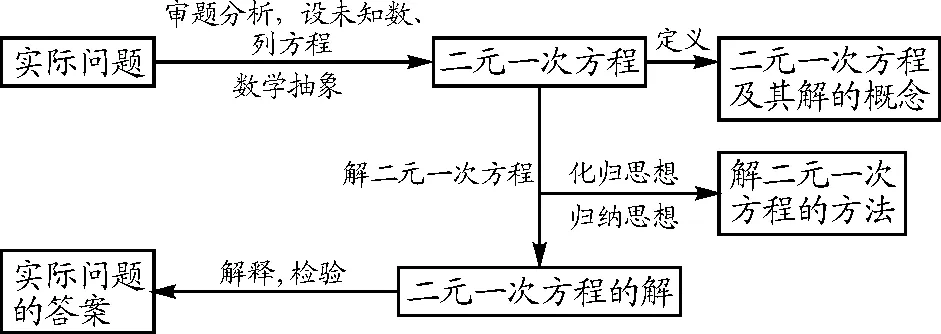
图1
(2)引导学生总结交流,认识到研究的方法和二元一次方程在实际生活中的运用,建构数学模型,积累利用方程解决问题的经验.
2 教学说明
本课中不仅带领学生认识了二元一次方程的概念,还引导学生探究了解二元一次方程的方法,在学习过程中渗透了数学的化归思想,使学生能将方程的知识应用到实际问题中,建构模型,解决具体问题.通过教师的引导和总结,学生总结出解二元一次方程的基本步骤,并反思内化,提升了认识.整个学习过程充分体现了学生的主体地位,学生在自主探究中积累了活动经验,提升了探究的能力.通过教学,实现了利用数学知识解决现实世界中的数量关系的教学目标,落实了学科的核心素养.本课将重点放在列方程和解方程的过程中,以学生的知识经验为基础,鼓励引导学生自主解决,提升了学生的学习力.
以上教学充分体现了关注过程教育的重要性,让学生充分体验知识的产生过程.同时,突出重点,突破难点,让学生感悟到二元一次方程在现实世界中的运用,体会到二元一次方程解的不唯一性,由具体到抽象,实现了认识的升华,体现了过程教育的价值.
