向思维更深处漫溯

［摘  要］ 小学数学教学是培养学生数学思维能力的过程。小学生的接受能力比较强，教师应根据教学内容精心设计各个教学环节，使教学过程环环相扣、螺旋上升，让学生的数学思维主动追随教师的引导而向更深处漫溯。

［关键词］ 周长；计算；转化；策略

在小学数学教学中，发展学生的思维能力成为课堂教学的重要目标之一。教师只有精心设计课堂教学内容，引领学生在学习过程中产生深度思考，才能有效地提升学生数学核心素养。探索“长方形和正方形周长”的计算方法是培养学生空间观念的重要内容，由于几何图形的周长知识比较抽象，对以形象思维见长的小学三年级学生来说是学习中的一大难点。笔者以苏教版三年级上册“长方形和正方形周长的计算”一课的教学为例，谈谈引领学生向思维更深处漫溯的策略，使数学课堂教学简约而生动。

一、关联旧知，启动思维

数学知识的学习过程是一个不断积累的过程，需要建立在学生已有的知识经验的基础上并逐步提升。在备课时，教师要认真研究教材内容，找到新旧知识的关联纽带，以旧知带动新知的学习，使课堂教学顺利起航。

用课件展示教材第41页例3。

师：这里呈现的是一幅篮球场的图片，请大家仔细观察并联系生活实际，说一说篮球场是一个什么形状的图形？

生1：篮球场都是长方形。

师：长方形有哪些特征呢？

生2：长方形有四条边，四个直角，长方形的对边相等。

师：再来读一读图上面的文字，这道题需要我们解决什么问题吗？

生3：这道题需要我们求出篮球场的周长，实际上就是求出这个长方形的周长。

师：我们已经学习过关于周长的知识，还记得我们是怎么测量图形的周长吗？

生4：计算出图形边线的长度，就能知道图形的周长。

师：在上一节课“认识周长”中，同学们都开动脑筋，想出了很多办法测量规则图形和不规则图形的周长。这一节课我们要学习“长方形和正方形周长的计算”，你准备用什么方法来计算这个篮球场的周长呢？

生1：用一根软尺绕着篮球场围一圈，读出软尺的最后刻度，就知道篮球场的周长了。

师：这根软尺一定要很长才行。

生2：根据周长的概念，只要把这个长方形的四条边的长度加起来就行。

生3：根据长方形对边相等的特征，先计算出两条长和两条宽，再把它们加起来就可以求出篮球场的周长了。

师：同学们的想法都很好，请大家用自己喜欢的方式求出这个篮球场的周长吧！

教师根据以前所学内容导入课题能激活学生已有的知识经验，让学生迅速勾连起与所学内容相关联的记忆，自主沟通知识之间的相互联系，这样的教学能促使学生把注意力转移到课堂上。学生激发出浓浓的学习兴趣，找到解决问题的方法，会愉快地进入新一轮的学习中来。

二、探究方法，暴露思维

数学新课标要求把课堂还给学生，要让学生成为课堂学习的主人。因此，在课堂教学中，教师要以学生为中心开展探究式教学，充分暴露学生的学习思维，将学生学习数学知识的过程一一呈现出来，从而把学生数学知识的学习过程演化成教师的数学活动的过程。

师：请大家踊跃交流计算篮球场周长的方法。

生1：篮球场的长是28米，宽是15米，我把四条边的长度依次相加：28＋15＋28＋15＝86（米），就算出了篮球场的周长。

师：你采用的计算方法是“长方形的周长＝长＋宽＋长＋宽”。（边说边板书）

生2：我的答题思路和他差不多，我是把两条长和两条宽加起来：28＋28＋15＋15＝86（米），就算出了篮球场的周长。

师：你采用的计算方法是“长方形的周长＝长＋长＋宽＋宽”。（边说边板书）

生3：因为篮球场有两条相等的长，两条相等的宽，我就先用28×2＝56（米）算出两条长，再用15×2＝30（米）算出两条宽的长度，最后把它们加起来：56＋30＝86（米），这样就算出了篮球场的周长。

师：你采用的计算方法是“长方形的周长＝长×2＋宽×2”。（边说边板书）

生4：我想，这个篮球场的对边相等，那我就先算出一条长和一条宽合起来的长度，28＋15＝43（米），再乘2就可以算出篮球场的周长，43×2＝86（米）。

师：你采用的计算方法是“长方形的周长＝（长＋宽）×2”。（边说边板书）

师：比较一下，这4种计算篮球场周长的方法，有什么异同点？

生5：这4种方法都能计算长方形一周的长度。

生6：这4种计算过程虽然不同，但结果相同。

师：你觉得这4种方法中，哪一种最简便？

生7：第4种方法计算步骤最少、最简便。

数学教学中，引导学生解决数学问题是教学的重点和难点，教师要组织学生开展探究活动。在讨论和交流中，教师要让学生对问题的分析及解决问题的思维过程充分暴露出来，不断优化问题的解决方法，让学生获得成功的喜悦感，从而树立学好数学的自信心。本案例以学生较为熟悉的篮球场为学习背景，提出计算篮球场周长的问题，引导他们交流长方形周长的计算方法，在暴露的思维中确认最佳计算方法，这样能使课堂上的数学活动具有挑战性，有利于吸引学生积极参与到学习中来。

三、探究问题，深入思維

学会了一定的方法以后，要是碰到新问题，学生就会跃跃欲试，充满挑战精神。在课堂上教师要利用学生的这一特点设置一些拓展题，让学生试着去“跳一跳，摘果子”，让学生的思维在探究的过程中逐步向纵深处发展。

师：通过刚才计算篮球场周长的活动，我们都掌握了长方形周长的计算方法。在此基础上，请大家试一试正方形的周长可以怎样计算呢？（课件展示教材第44页的“试一试”）

生1：这块手帕是正方形，求它的周长，就是求正方形的周长，我可以把四条边的长度加起来，25＋25＋25＋25＝100（厘米）。

师：你采用的计算方法是“正方形的周长＝边长＋边长＋边长＋边长”。

生2：因为手帕的每一条边的长度都相等，我还可以用乘法来计算，25×4＝100（厘米）。

师：你采用的计算方法是“正方形周长＝边长×4”。

师：这两种计算正方形周长的方法，你更喜欢哪一种呢？

生3：我喜欢第二种，因为第二种用乘法计算更加方便。

师：现在，我们学会了求长方形和正方形的周长，就有信心去解决更多的问题了。请大家观察这两幅图（图1和图2），你认为两个图形的周长是什么关系？

生1：图1的周长比图2的周长要长。

生2：不对，我计算了一下，图1的周长有4×4＝16（厘米）。再仔细数一数，图2的周长也是16厘米，它们的周长是相等的。

师：为什么会出现两种不同的答案？请大家根据刚才所学的知识进行探究。

生1：我一开始觉得图1的图形比图2大，所以就想当然地认为图1的周长要长一点。但是周长应该是计算一周边线的长度，不能根据图形大小来判断，所以我的答案是错误的。

生2：我采用数学的转化思想，把图2中右上角的小横线向上移动一格，把小竖线向右移动一格，这样就把图2的周长变成和图1一样了，所以它们的周长是相等的。

师：请你到多媒体屏幕上画一画。（学生上台操作）

师：遇到这种不规则图形时，我们就尽量把它转变为规则图形，在数学上称为“转化”。利用这种“转化”思想，能够给我们的学习带来很多方便。

数学课堂教学中的问题探究是搭建学生思维的阶梯，它是学生学习的内驱力。在以核心问题为主线，主动寻找解决问题的路径与方法的过程中，学生的体验得到内化，分析思辨能力也会随之提升。三年级学生的思维并不成熟，因而在课堂学习中难免会磕磕碰碰，有时还会走弯路，但是通过互相交流、探讨，学生的思维在不断得到修正，逐步朝着深处发展。

四、变式练习，提升思维

如果只满足于基本知识的掌握，那么学生容易滋生自我满足感，数学思维就会裹足不前。因此，教师还应该在课堂上适当地让学生完成一些变式训练，引导他们在积极的探索中提升思维能力。

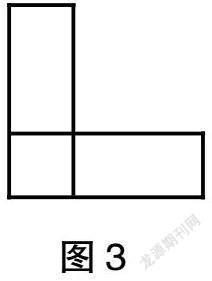
师：如图3，这是由两个长5厘米、宽2厘米的长方形重叠成的图形。你能算出这个图形的周长吗？

生1：我先算出一个长方形的周长（5＋2）×2＝14（厘米），两个长方形的周长就是14×2＝28（厘米）。

生2：这样计算不对，这两个长方形重叠以后组合成新图形，新图形的周长就不再是原有的两个长方形的周长之和了。

师：说得有道理。请大家开动脑筋，怎么计算这个新图形的周长呢？

生3：我把这个图形的周长用红线描出来，就是这样的图形（如图4），它由六条长短不一的边组成。通过观察，我发现最长的两条边还是5厘米，最短的两条边还是2厘米，第二长的两条边因为有一部分被遮住了，所以在新图形中的长度是5－2＝3（厘米），因而这个新图形的周长是5＋5＋2＋3＋3＋2＝20（厘米）。

师：把图形重新画了以后，怎么求出它的周长，我们的思路就变得非常清晰了。

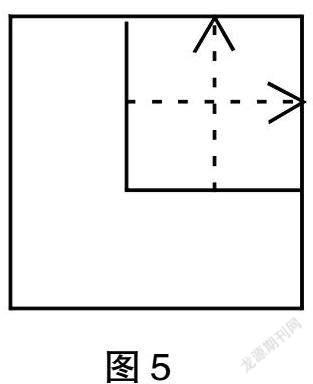
生2：我受到刚才解题的启发，把第二长的两条边分别向上、向右移动，就转化成求一个正方形的周长。如图5所示，这样就可以直接用乘法算式5×4＝20（厘米），求出这个新图形的周长。

师：你又想到了利用数学转化思想来解决问题，真不错！

训练学生的多维思维，变式练习是关键，它能促进学生主动思考，让学生发现知识之间的联系和差异，帮助学生举一反三、触类旁通、以不变应万变，从而形成自己的认知体系。上述案例中通过解决一个个具体的问题，使学生的数学思维得到了激烈的碰撞，并在不断思考、探究、分析、证实中让思维变得更加严密、灵活、深刻。

思維能力是学习数学的核心能力，培养学生的思维能力是数学教学的一项重要任务。因此教师一定要认真研究教材，以生为本，有针对性地设计练习梯度，让学生在自主探究、踊跃展示中打开学习视野，向思维更深处漫溯。

作者简介：管勤燕（1977—），本科学历，一级教师，从事小学数学教学工作。