基于V形沟槽的机翼蒙皮减阻特性仿真分析

摘要： 为减少飞机飞行阻力、提高气动效率，基于微沟槽减阻理论，对机翼蒙皮进行微沟槽设计和减阻特性分析。应用计算流体力学（Computational Fluid Dynamics，CFD）方法，对不可压缩流下的纵、横向微沟槽进行模拟。选取k-ω SST湍流模型，通过分析V形沟槽边界层区域的流动特征，探究不同尺寸V形沟槽的减阻特性与减阻机理，对横向V形沟槽的数量与位置进行优化设计。仿真结果表明，随着沟槽尺寸和迎角减小，减阻率增大，纵向沟槽最大减阻率可达9.31%，横向沟槽减阻率最大可达7.35%，优化后的沟槽减阻率提高了1.39%。

关键词： V形沟槽；机翼蒙皮；k-ωSST模型；减阻机理；仿真分析

中图分类号： V262" " " " 文献标志码： A

doi：10.3969/j.issn.2095-1248.2023.02.010

Simulation analysis of drag reduction characteristics for wing skin based on V-shaped groove

WANG Wei， HUANG Ru， ZHOU Ai， FENG He

（College of Civil Aviation， Shenyang Aerospace University， Shenyang 110136，China）

Abstract： In order to reduce the aircraft flight resistance and improve its aerodynamic efficiency， based on the micro-groove drag reduction theory， the micro-groove design and drag reduction characteristics analysis of the wing skin were conducted. The incompressible flows of longitudinal and transverse micro-groove were simulated using computational fluid dynamics （CFD） methods. The k-ω SST model was selected，and the drag reduction characteristics and mechanism on different sizes of V-shaped groove were investigated. By investigating the flow characteristics in the boundary layer， the number and position of transverse V-shaped groove were optimized. The results show that the drag reduction rate is increased with the decrease of groove size and angle of attack. The maximum drag reduction rate of longitudinal and transverse grooves are 9.31% and 7.35% respectively，and this rate of the optimized transverse groove is increased by 1.39%.

Key words： V-shaped groove；wing skin；k-ω SST model；drag reduction mechanism；simulation analysis

飞行阻力是影响民航客机燃油经济性的重要因素，增升减阻、改善飞行性能、提高燃油效率一直是民航客机设计的主要目标［1-2］。为减少飞行时的摩擦阻力，国内外学者与研究机构基于仿生学原理，研究仿生微结构在飞行器减阻作用中的应用。

目前，仿生微结构减阻的相关研究主要集中在微沟槽结构。美国NASA研究中心的Walsh［3］对三角形截面微沟槽减阻效果进行分析，最高减阻率可达8%。Bacher等［4］采用流动显示与热膜流速器对沟槽模型进行减阻研究，分析流体流线，得出沟槽结构的减阻机理。Bixier等［5］对封闭管道内的微沟槽进行减阻实验，得出来流速度、流体黏性以及微沟槽形状对减阻率的影响规律。Martin等［6］与Domel等［7］基于仿生学原理设计微沟槽，得到具有最佳减阻效果的沟槽形状、尺寸设计参数。周健等［8］对微沟槽减阻特性进行模拟分析，通过与实验结果对比，验证了模拟分析方法的正确性，解决了模拟分析方法在工程实践中的应用问题。王松岭等［9］基于大涡模拟方法，探究沟槽分布位置对机翼气动特性的影响，发现分布于机翼后段的沟槽可有效控制边界层分离，改善气动性能。陈璠等［10］与徐琰等［11］基于数值模拟方法，研究多种形状沟槽的减阻特性，解释沟槽的减阻机理，徐琰进一步给出最优V形沟槽设计方案。杜淑雅等［12］分别采用RANS、DES、LES和直接模拟方法，对三角形、梯形两种沟槽进行仿真，对比得出梯形沟槽减阻效果更优的结论。

上述研究对不同截面形状沟槽进行减阻分析，通过改变来流速度、迎角大小或沟槽尺寸等单一方式分析减阻规律。本文将横、纵向V形沟槽分别应用于机翼蒙皮，从来流速度、迎角、沟槽间距与高度、沟槽数目与位置等参数对其进行减阻特性研究。通过仿真计算得出横向与纵向V形沟槽随来流速度、迎角与沟槽尺寸的变化规律，通过分析近壁面的流场特性，得出横向、纵向沟槽的减阻机理。改变横向沟槽的数目、距前缘的距离，进一步提升横向沟槽的减阻率。

1 沟槽结构设计

由于气流的黏性作用，在流动过程中物体表面流速降低，随着与壁面间距离的增大，逐渐达到来流速度，形成附着在物体表面的薄流体层，即边界层，在流体计算中不可忽略。如图1所示，其厚度用δ表示。

正将边界层分为黏性底层、过渡层、对数率层，以无量纲距离y+值为基准

y^+=（yu_τ）/v （1）

式中：y为距壁面距离；uτ为表面剪切速度；v为运动黏度。流体在黏性底层的流动近似于层流，湍流切应力可忽略不计。随着流体与壁面距离的增大，需要考虑湍流切应力与黏性切应力两者的作用，对速率层的流体处于完全湍流状态，此时湍流切应力起主要作用［13］。

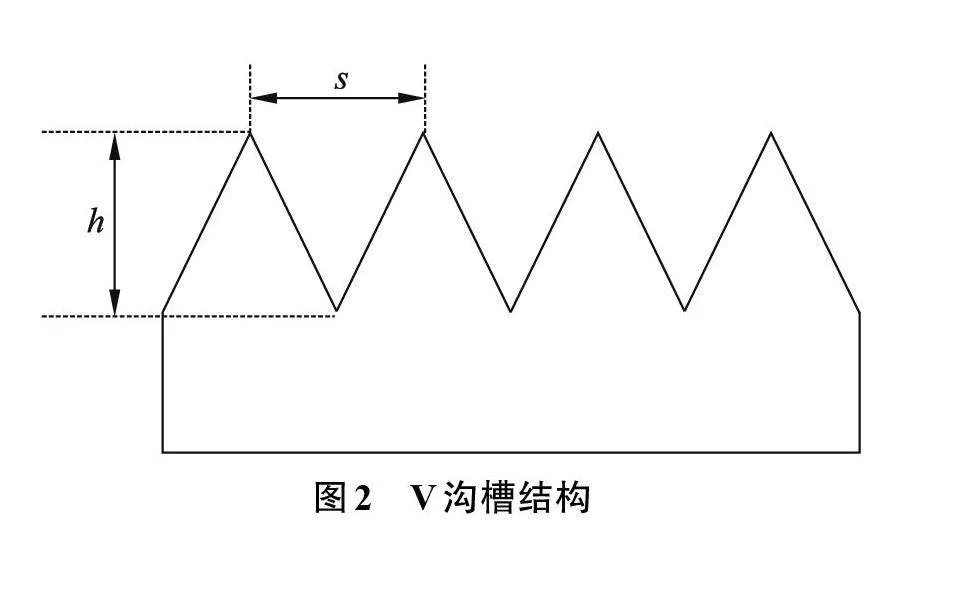
本文以V形为例，通过沟槽的高度和间距来确定沟槽尺寸，沟槽结构如图2所示。当无量纲数h+=s+时，沟槽的减阻性能最佳［14］。

计算公式

h^+=h u_τ/v （2）

s^+=s u_τ/v （3）

式中：s为沟槽间距；h为沟槽高度；u_τ=√（τ_ω/ρ）

壁面剪切应力τω满足

τ_ω=0.022 5ρU^2 （v/Uδ）^（1/4） （4）

式中：U为流体速度。

边界层厚度δ表示为

δ=0.37×Re_^（-1/5） （5）

式中：Re为雷诺数，结合式（2）～（5），最终得出沟槽无量纲高度和间距如式（6）、（7）所示

h^+=（0.17hURe^（-1/10））/v （6）

s^+=（0.17sURe^（-1/10））/v （7）

2 湍流模型

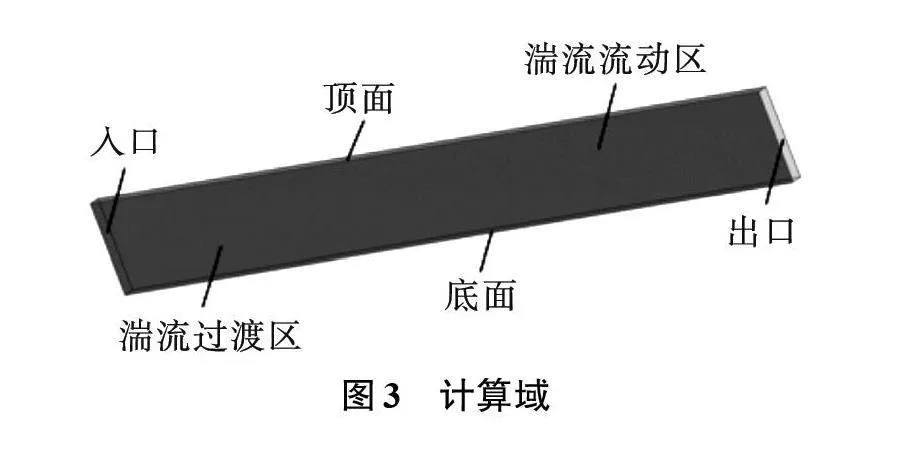
利用光滑平面雷诺数计算公式与边界层厚度公式可知，临界雷诺数为5.0×105，流体最小流速为80 m/s，计算域的长度需要大于92.5 mm，计算域的边界层厚度为3 mm。如图3所示，设置计算域长为140 mm、高20 mm、宽2 mm。

在前处理阶段选择ICEM完成网格划分工作。非结构网格可以灵活、高效地控制网格大小，完成边界层部分的网格加密工作，此步操作在最大程度上提高了计算结果的准确度。网格划分结果如图4所示。

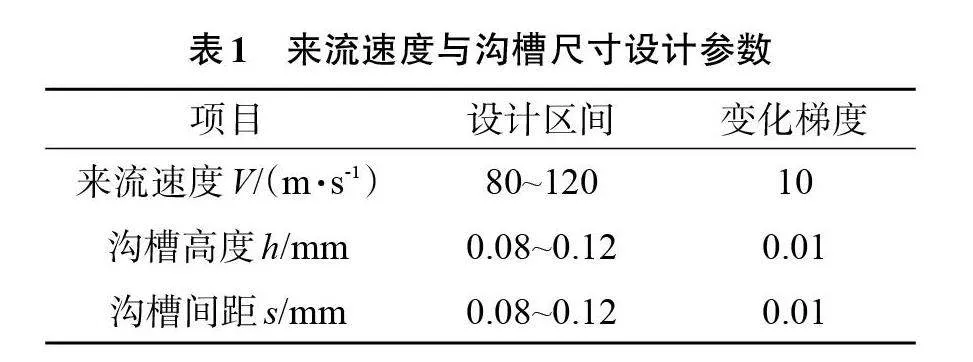
选择k-ω SST两方程湍流模型［15］进行计算，该模型融合了k-ε与k-ω两种计算模型的优点，计算过程中考虑了湍流切应力的传输，在充分模拟远壁面湍流流动的同时，更加准确地模拟出边界层附近的流体动线。计算域中的流体为密度ρ=1.225 kg/m3、动力黏度μ=1.789×105" N∙s/m2、运动黏度v=1.46×105 m2/s的不可压缩空气。设定速度入口与压力出口，来流速度从80 m/s开始，以10 m/s为一个梯度增加到120 m/s；迎角的大小从-5°开始，以5°为一个梯度增加到15°；设置湍流强度为5%、湍流黏度比为10。采用混合初始化及SIMPLE算法进行计算。

3 仿真结果与减阻机理

针对来流速度、迎角大小、沟槽的尺寸、数目、位置等影响因素对沟槽减阻率进行求解，沟槽减阻率η如式（8）所示

η=（F-F_1）/F×100% （8）

式中：F为光滑蒙皮所受阻力；F1为V型沟槽蒙皮所受阻力。减阻率越大，减阻效果越好。

设定沟槽数为10，横向V形沟槽在距离前缘80 mm处。根据表1中设计参数分别对沟槽进行仿真计算，结果如图5所示。横向沟槽减阻率随着来流速度的增加先增大后减小，在来流速度为100 m/s时出现拐点，在沟槽为h=s=0.08 mm、V=100 m/s时，减阻率达到最大值6.81%；纵向沟槽减阻率随速度的增大而减小，在h=s=0.08、V=80 m/s时，减阻率达到最大值8.75%。随着沟槽尺寸减小，沟槽减阻率增大。

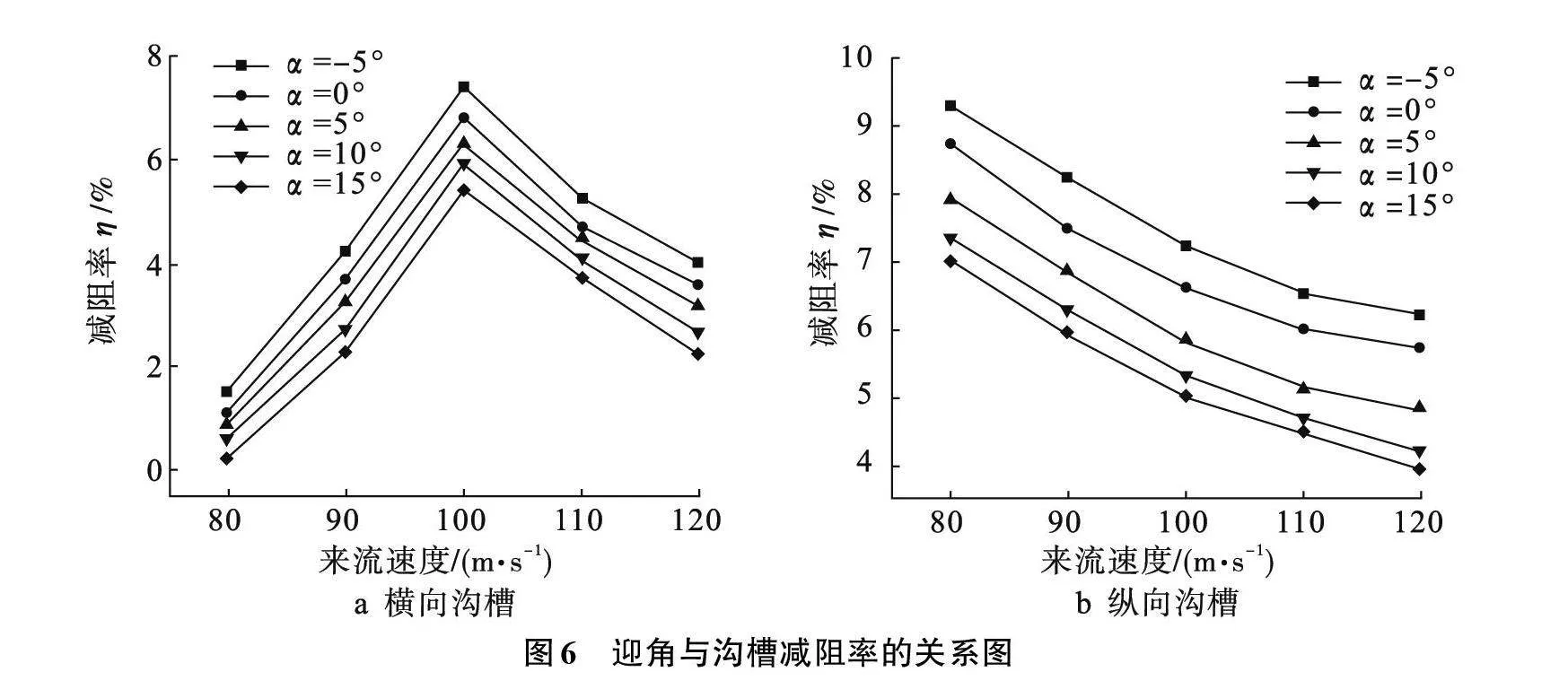
针对h=s=0.08mm沟槽，根据表2中设计的参数对不同迎角条件下的沟槽进行仿真计算，结果如图6所示。迎角为-5°时沟槽减阻率最大，随着来流速度的增加，横向沟槽减阻率的变化拐点依然存在，当来流速度V=100 m/s时达到最大即7.35%；纵向沟槽随速度的增大，减阻率减小，当来流速度V=80 m/s时，减阻率最大值为9.31%。随着机翼的迎角减小，沟槽减阻率增大。

以提高横向沟槽减阻率为目的，沟槽数目、距前缘距离为设计参数，对h=s=0.08 mm横向沟槽在迎角0°，来流速度分别为80、100、120 m/s条件下进行优化设计。沟槽数目设计参数如表3所示，仿真计算结果如图7所示。随着沟槽数目的增加，沟槽减阻率增大。当V=80 m/s时，沟槽减阻率最小；当V=100 m/s时，平均沟槽减阻率最大，最大值达到8.74%。

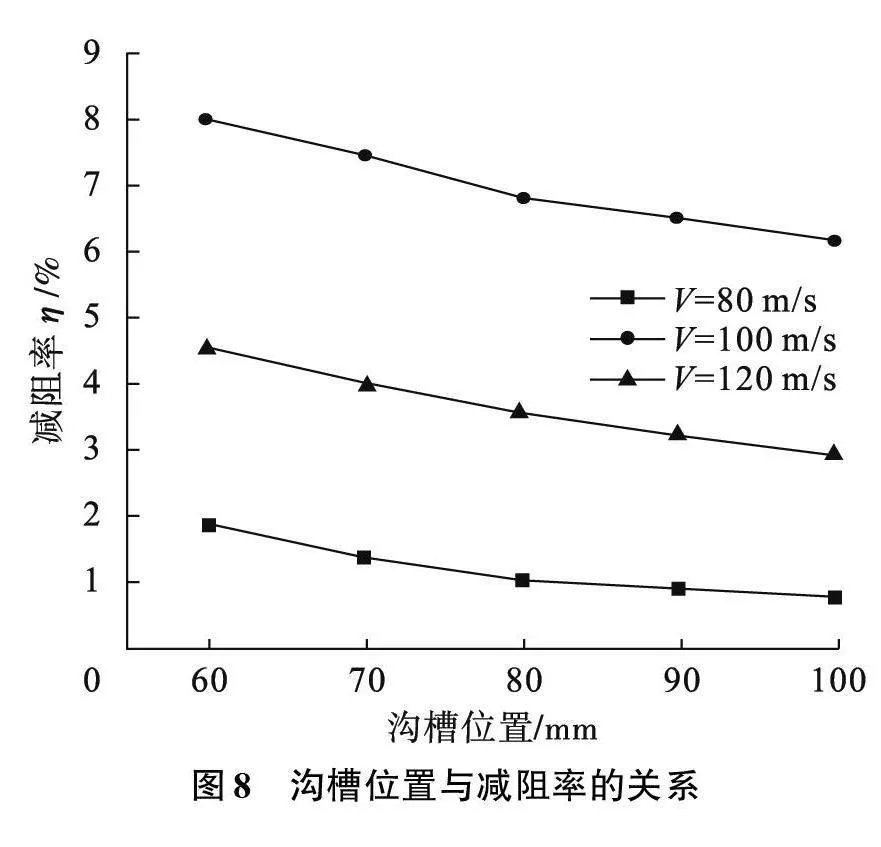
针对沟槽距离前缘位置，根据表4设计参数对横向沟槽进行仿真计算，仿真结果如图8所示。沟槽分布位置对减阻率的影响较小，随着与前缘距离的增加，减阻率整体呈下降趋势。在距前缘为60 mm、V=100 m/s时，平均减阻率最大，最大减阻率达8.01%。在V=80 m/s时，减阻率提升了0.84%，最高达1.86%。V=120 m/s时，减阻率提升了0.96%，最高达4.51%。横向沟槽分布位置越接近前缘，其减阻效果越好。

光滑蒙皮表面与横向沟槽蒙皮表面的速度云图如图9所示，横向微沟槽加大了边界层厚度，从而改变了边界层内部气流流线，进而达到改善气动性能的效果。气流流过沟槽时，一部分气流流进沟槽内部，在沟槽底部形成低速漩涡，沟槽内部的旋转气流起到了类似“滚动轴承”［16］的作用，蒙皮外表面的气流流动状态由滑动摩擦转变为滚动摩擦。

光滑蒙皮表面与纵向沟槽蒙皮表面的速度云图如图10所示。纵向微沟槽同样增大了蒙皮表面边界层厚度，黏性底层厚度增加，气流流速变化梯度减小，该区域气流流动平缓，流动特征近似于层流，可让外侧高速气流顺利流过壁面且与壁面不发生接触，减少了与壁面间的摩擦阻力。黏性底层的加厚抑制了湍流的产生，达到减阻目的。

4 结论

以V形沟槽机翼蒙皮为研究对象，在不可压缩流场中进行仿真分析，得出沟槽减阻规律与减阻机理，设计提高横向V沟槽减阻效果方案。本文所得结论如下：

（1）沟槽尺寸越小，减阻效果越好。沟槽h=s=0.08 mm时，减阻效果最佳，横向V沟槽减阻率随速度的增大先增大后减小，在V=100 m/s时达到最大6.81%，纵向V沟槽减阻率则随着速度的增大而减小，最大达8.75%。随着迎角的减小沟槽减阻率增大。α=-5°时，横向沟槽减阻率达7.35%，纵向沟槽减阻率可达9.31%。

（2）增加沟槽数目、缩短与前缘距离可提高横向沟槽减阻率。沟槽数目增加至25，沟槽减阻率增加到8.74%。沟槽距前缘距离为60 mm时，最大减阻率达8.01%。

（3）横向V沟槽近壁面气流在沟槽内形成低速漩涡，将壁面与流体之间的滑动摩擦转化成滚动摩擦，减小了气流与壁面间的摩擦阻力，达到减阻目的。纵向V沟槽使得边界层的黏性底层加厚，气流速度变化梯度减小，黏性切应力减小，气流流动更加平缓，避免了外侧高速气流与壁面间产生摩擦阻力，达到减阻目的。

参考文献（References）：

［1］ 陈耿.飞机减阻技术的现状与发展［J］.科技与创新，2019（21）：42-44．

［2］ 陈迎春，张美红，张淼，等.大型客机气动设计综述［J］.航空学报，2019，40（1）：30-46．

［3］ Walsh M J.Riblets as a viscous drag reduction technique［J］.AIAA Journal，1983，21（4）：485-486．

［4］ Bacher E，Smith C.A combined visualization⁃anemometry study of the turbulent drag reducing mechanisms of triangular micro-groove surface modifications［C］//Shear Flow Control Conference.Boulder，USA：AIAA，1985．

［5］ Bixler G D，Bhushan B.Shark skin inspired low⁃drag microstructured surfaces in closed channel flow［J］.Journal of Colloid and Interface Science，2013，393（10）：384-396．

［6］ Martin S，Bhushan B.Fluid flow analysis of a shark⁃inspired microstructure［J］.Journal of Fluid Mechanics，2014，756：5-29．

［7］ Domel A G，Saadat M，Weaver J C，et al.Shark skin⁃inspired designs that improve aerodynamic performance［J］.Journal of the Royal Society，Interface，2018，15（139）：20170828．

［8］ 周健，欧平，刘沛清，等.沟槽面湍流减阻数值评估方法［J］.航空学报，2017，38（4）：10-21.

［9］ 王松岭，张开顺，吴正人，等.基于大涡模拟方法仿生翼型气动特性数值模拟［J］.科学技术与工程，2018，18（19）：296-300.

［10］ 陈璠，徐朋飞．“仿生学” 沟槽减阻仿真分析及机理研究［J］.航空发动机，2021，47（2）：28-32.

［11］ 徐琰，张臣，汪子轩.局部近似平面V型沟槽减阻特性数值模拟研究［J］.航空制造技术，2021，64（15）：86-99.

［12］ 杜淑雅，桑为民，庞润.基于数值模拟的2种条纹沟槽减阻特性对比分析［J］.西北工业大学学报，2022，40（2）：261-270.

［13］ Robinson S K.Coherent motions in the turbulent boundary layer［J］.Annual Review of Fluid Mechanics，1991，23（1）：601-639．

［14］ 时雪梅.沟槽表面减阻特性的数值模拟研究［D］.南京：南京航空航天大学，2019．

［15］ 曾宇，汪洪波，孙明波，等.SST湍流模型改进研究综述［J/OL］.航空学报，2022，43（10）：1-32.（2022-07-26）［2022-10-17］.https：//hkxb.buaa.edu.cn/CN/10.7527/S1000-6893.2022-27411.

［16］ 谭惠丰，康敬天，卫剑征，等.三角形微沟槽飞艇蒙皮表面的流场分析［J］.哈尔滨工业大学学报，2014，46（7）：32-35.

（责任编辑：吴萍" 英文审校：杜一鸣）