基于事件列表递归比较的复杂事件匹配方法

摘要： 针对现有复杂事件匹配处理方法存在匹配代价高的问题，提出了一种在有序事件列表上选择最佳匹配顺序进行递归遍历的复杂事件匹配方法OptiSeq。将事件实例按照查询模式中不同事件类型缓存到有序事件列表中，并通过事件列表中事件实例的数量选择最优的查询匹配起点及查询匹配顺序，之后在有序列表上对不同约束分别进行递归校验，最终输出完全满足查询模式的所有复杂事件结果。该方法克服了使用自动机模型固定状态转换的弊端，也避免了使用树型模型批处理操作漏解的问题，并且合理优化了匹配顺序，进一步提高查询匹配效率。在模拟数据集和真实数据集上进行了实验测试与分析，与当前流行的SASE、Siddhi两种复杂事件处理方法进行比较。实验表明，所提出的方法能够在保证匹配正确性的同时，有效地减少匹配过程中的冗余计算，提高整体匹配效率。

关键词： 复杂事件匹配；递归比较；有序事件列表；查询过滤；属性验证

中图分类号： TP315" " " " 文献标志码： A

doi：10.3969/j.issn.2095-1248.2023.02.005

Complex event matching based on recursive comparison of event list

XIA Xiu-feng， DING Jian-li， QIU Tao， XIE Pei-liang

（College of Computer Science， Shenyang Aerospace University， Shenyang 110136，China）

Abstract： Aiming at the problem of high matching cost in the existing complex event matching processing methods， a complex event matching method OptiSeq was proposed， which selected the best matching order on the ordered event list for recursive traversal. The event instances were cached in the ordered event list according to the different event types in the query mode， and the optimal query matching starting point and query matching order were selected by judging the number of event instan ces in the event list. Then， the OptiSeq method performed recursive validation and ultimately output all complex event results that fully met the query pattern.This method overcame the drawbacks of using automata model to fix state transitions， and also avoided the problem of missing solutions in batch operations using tree models， and optimized the matching order reasonably， further improved query matching efficiency. Experiments were tested and analyzed on simulated datasets and real datasets， and compared with the current popular SASE and Siddhi complex event processing methods. The experiments show that the proposed method can effectively reduce the redundant calculations in the matching process and improve the overall matching efficiency while ensuring the correctness of matching.

Key words： complex event matching；recursive comparison；ordered event list；query filtering；attribute verification

随着信息技术产业发展的进一步深化及物联网技术、传感器网络和射频识别等技术与应用的快速发展，大规模的流式数据从各式各样的应用系统中不断产生和涌现，包括设备运行状态数据、企业信息化数据、生产参数数据等。面对这些大量的描述性物理数据，用户迫切地希望能够在这些海量数据中及时发现、挖掘一些有意义的数据，如何根据特定的匹配条件高效地获取并处理有价值的数据信息成为研究的热点，复杂事件匹配处理技术也因此应运而生。例如在股票交易信息分析［1］、道路交通规划［2］、传感器网络［3］、数控机床系统［4］和海量航天数据分析［5］等方面都有广泛的应用。

尽管目前已有一些复杂事件匹配处理方法，例如SASE［6-7］、ZStream［8］、Siddhi［9］等，但这些方法在处理简单查询模式下的事件匹配时存在一定局限性。SASE方法将查询转化为一种自动机模型，其自然表达方式是一系列状态转换。显然这种固定的状态转换形式限制了事件匹配的顺序，使事件处理的灵活性有很大的限制。一旦查询模式中存在否定事件类型与非否定事件类型之间的关联约束时，固定处理顺序的状态转换模式很难直接跨过否定事件状态去执行后续事件状态的匹配操作。ZStream是基于树型模型的方法，虽然克服了自动机的固定状态转换操作，但也存在中间结果数量多、大量重复计算、批处理操作漏解等问题。另外，目前大多数方法都没有研究最佳的查询匹配顺序，仅按照查询模式下目标序列的顺序执行复杂事件查询匹配操作。

为了既能满足现有的复杂事件匹配处理的需求，又能进一步提高复杂事件匹配的效率，本文提出了一种在有序事件列表上选择最佳匹配顺序进行递归遍历的复杂事件匹配方法。不同于现有的转换模型，该方法在有序事件列表上执行操作，即将有序事件列表作为事件流中事件实例的有序缓冲区，同时优化了查询匹配顺序，通过判别事件列表中事件实例数量，来选择对查询计划最优的查询匹配起点及更优的查询匹配顺序。

1 相关工作

复杂事件处理是从事件驱动业务出发的，将系统中产生的每一条数据记录都看成是一个事件，复杂事件执行引擎会根据事先制定好的描述规则对事件流进行相应的判断、过滤、关联等操作，然后给用户输出一系列更高层次的复合事件。其中复杂事件描述规则一般包含用户感兴趣的事件语义或专业领域中某种既定的标准和规范。也就是说，复杂事件能够在实时事件流中处理识别某个人为定义的复合事件，并向用户反馈识别的结果。近年来，随着复杂事件处理技术的广泛使用，国内外针对此问题的研究方法也被陆续提出，由Giatrakos等［10］的总结工作发现，目前现有的复杂事件处理技术大致可以概括为基于自动机模型、基于逻辑模型以及基于树的模型3类。

基于自动机模型的处理方法是当前研究工作中最多的一类技术，例如Diao等［11］提出的SASE方法以及其衍生研究SASE+方法、Demers等［12-13］提出的Cayuga方法、Siddhi方法以及应用到工业中的Flink CEP［14］方法等。此类方法均把查询模式转换在自动机模型上进行操作，将查询模式表示为一系列必须检测的状态，当且仅当状态转换为终止状态时，才产生匹配结果。自动机方法存在一定的局限性，因为自动机的自然表达方式是一系列状态转换，因此此类方法强加了由该状态转换图确定的固定评估顺序。这不仅导致复杂事件查询处理灵活性降低，也会使否定操作的处理难以在状态中简单地完成，同时也很难支持并发事件即联合查询的处理。

与自动机相比，基于逻辑的复杂事件处理系统关注点有所不同，此类方法倾向于忽略查询规则中各种选择和消费策略的存在，关注的是事件发生的时序逻辑关系。例如Dousson［15］提出的CRS方法、Artikis等［16］提出的RTEC方法等。基于逻辑的方法本质上是一组由时间限制联系在一起的事件，其发生可能取决于上下文在时间逻辑上的推理，因此除了时间限制外，这类方法很难支持包含数学运算符、属性条件约束等条件的操作。

基于树型模型的处理方法是利用树的查询计划结构来表示复杂事件查询模式，例如Yuan 等提出的ZStream方法［8］、Liu等［17］提出的E-Cube方法、喻学军等［18］提出的Esper方法，还有郑利强等［19］研究的针对正规树模式的复杂事件查询方法等。这类方法将查询模式解析并转换为树型结构的表示形式，叶缓冲区用来存储来自事件流的原始事件实例，内部节点缓冲区存储来自子树缓冲区、满足一定查询模式的中间结果组合。虽然使用树型结构模型可以解决固定状态转换不足的问题，使得复杂事件处理操作更加灵活，但事实上这类方法依旧存在着大量的重复计算，批处理操作存在漏解等弊端。

基于以上研究可以发现，无论是基于自动机还是基于树的方法来实现复杂事件处理，为保证复杂事件匹配结果的正确性和完整性，均需要存储大量的事件实例或进行大量的重复匹配，给处理器计算能力和存储器等硬件资源都带来了不小的负荷。因此本文寻求一种既能满足现有复杂事件的匹配处理需求，又能进一步提高匹配效率的复杂事件处理方法。

2 预备知识

定义1" 事件流 事件流S（s1，s2，…，sn）由一系列的基本事件实例构成。其中si∈S，为事件实例，它包含了事件的类型、属性和事件发生时的时间戳等信息。本文使用大写英文字母表示基本事件类型（如事件类型A、事件类型B），事件实例则用相应的小写字母表示 （如A的事件实例a、B的事件实例b） ，如图1所示。

定义2" 简单事件与复杂事件 事件包含简单事件和复杂事件。简单事件可以看作一个活动点的发生，它不包含事件关系；而复杂事件是简单事件通过事件关系进行组合的更深层次事件。

定义3" 复杂事件查询模式 复杂事件查询模式Q由一组定义在基本事件上的约束条件构成，用以表示客观存在的目标事件的属性特征。

Grea等［20］的研究工作中已提出多种形式的复杂事件描述语言，用于定义复杂事件查询，其中SASE提出了最具有代表性的复杂事件描述语言，本文沿用SASE的语言形式，总体结构如下：

PATTERN lt;目标序列形式gt;

WHERE lt;属性约束条件gt;

WITHIN lt;时间窗口大小gt;

RETURN lt;输出表达形式gt;

其中，目标序列形式定义了复杂事件处理结果需满足基本形式以及序列查询操作（例如顺序操作、否定操作等），属性约束条件限制了事件实例在事件属性上需要满足的约束条件，时间窗口大小约束了复杂事件结果中事件实例发生的时间间隔，输出表达形式表明了输出结果样式。本文采用的查询模式中PATTERN子句能够支持3种序列操作，用以描述不同情况下的事件序列，序列操作的具体描述如下：

（1） 顺序操作（A；B）

表示A类型的事件实例a发生之后，有B类型的事件实例b在其后发生，即其发生的时间戳满足条件a.timestamplt;b.timestamp，并且满足时间范围约束b.timestamp-a.timestamp≤tw。

（2） 否定操作（！A）

表示A事件类型的事件实例不发生。例如查询模式“A；！B；C”表示C事件类型的事件实例c跟随在A事件类型的事件实例a之后发生，即a.timestamplt;c.timestamp，且在这之间没有b的事件实例发生。

（3） 闭包操作（Ak）

表示A事件类型中的事件实例连续发生至少k次。例如，对于查询“A；Bk；C”，要求在事件实例a与c之间存在至少k个事件实例b。

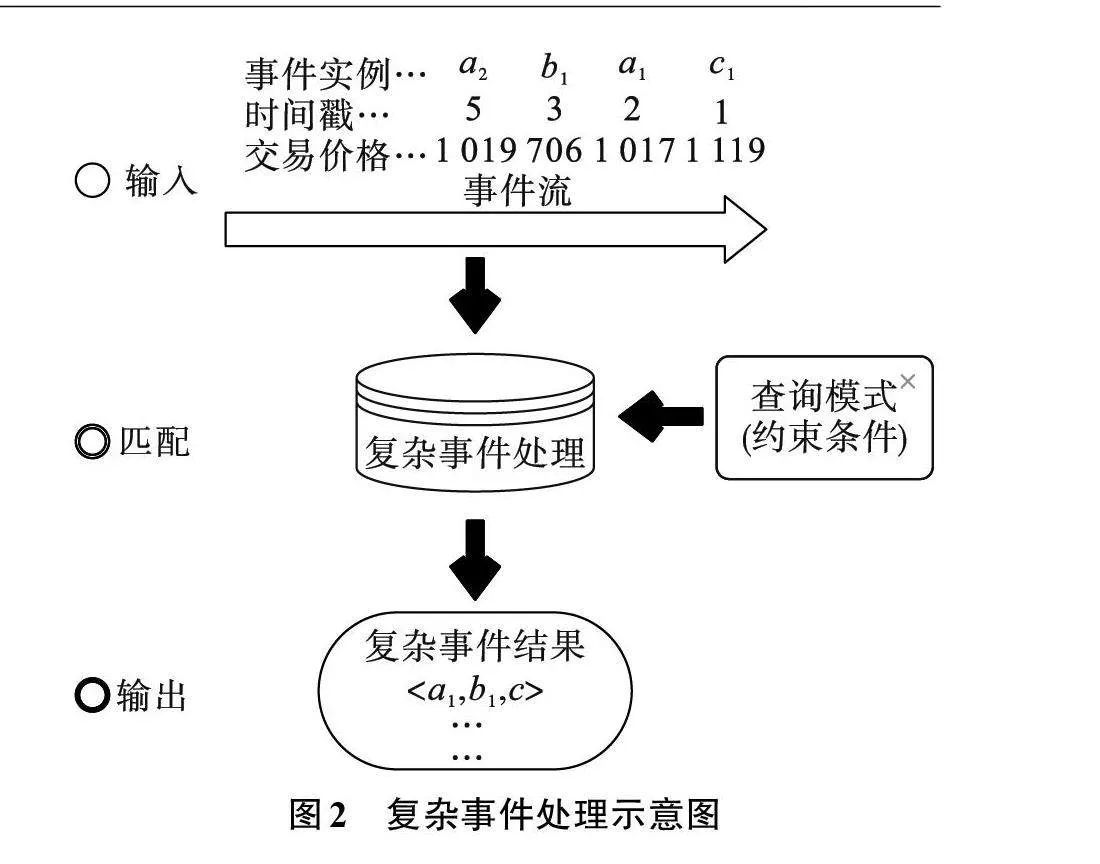
定义4" 复杂事件匹配问题 给定事件流S、复杂事件查询模式Q，复杂事件匹配处理即根据查询模式Q中给定的各类约束条件，在事件流S的基本事件实例中匹配出满足所有约束条件的全部复杂事件结果，如图2所示。

例1" 股票交易中的查询模式。用户想在众多繁杂的交易数据当中找到想要的交易记录，从而分析股票交易数据。将股票交易市场的交易数据作为事件流，给定的查询模式Q为

Q ： PATTERN A；B；C；D

WHERE a.pricegt;x

AND a.pricegt;（1+y%）×b.price

AND c.pricelt;（1-z%）×d.price

WITHIN 10 min

RETURN A，B，C，D

上述查询模式Q中，PATTERN子句表示关心的股票交易情况，其中发生的事件要满足 （A；B；C；D）的序列形式，即A、B、C、D这4种类型股票要先后有序地发生。WHERE子句定义了股票事件实例的股票交易价格属性的约束条件，即A型股票交易价格在x元以上，A种股票的交易价格大于B型股票的y个百分比涨幅后的价格，且C型股票交易价格低于D型股票在z个百分比跌幅后的价格。WITHIN子句限制了该事件发生的时间在10分钟之内。最后要求输出的复杂事件结果是以（A；B；C；D）的格式输出所有满足的复杂事件集合。

3 查询匹配计划

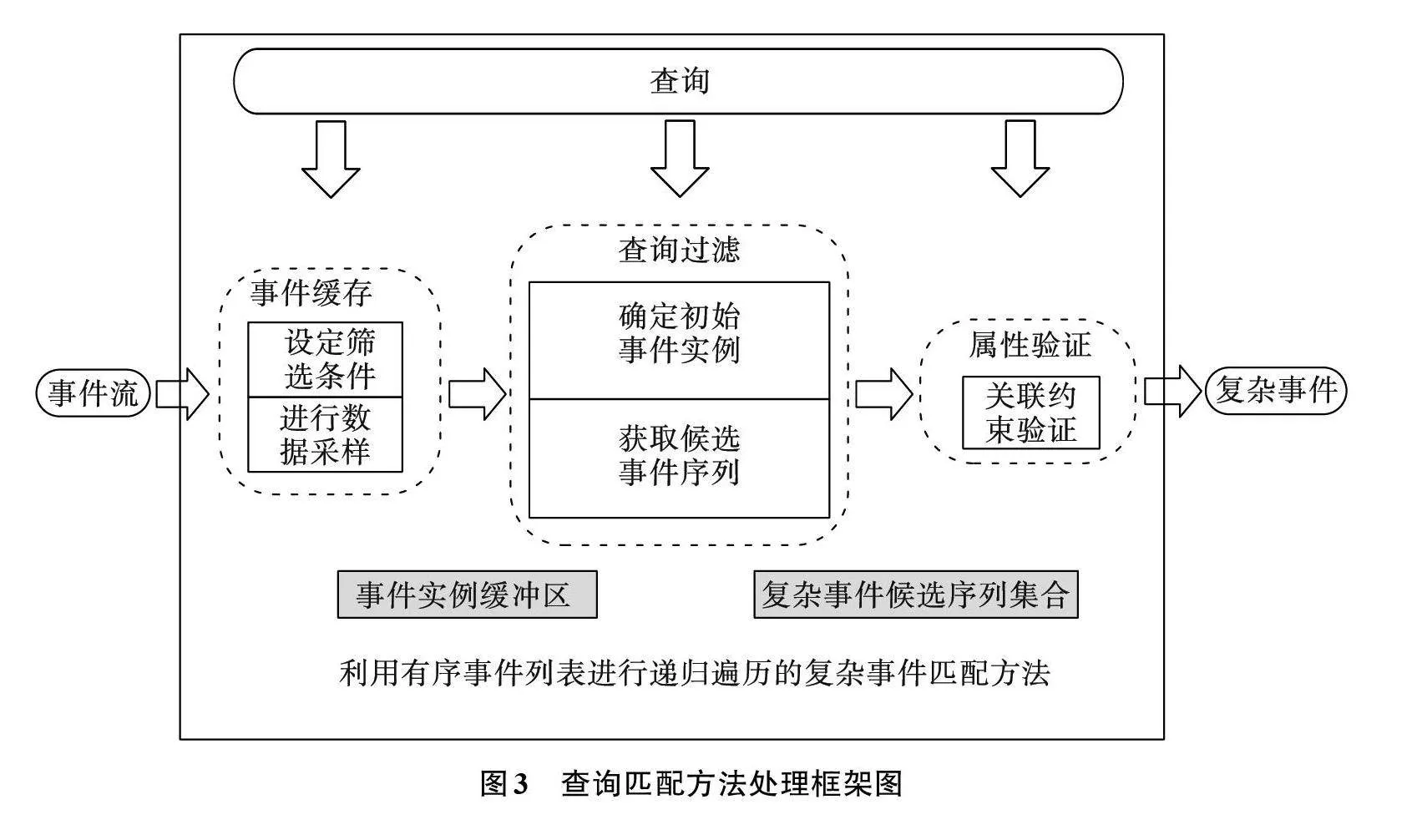
本节在有序事件列表上选择最佳匹配顺序，并通过递归遍历进行复杂事件匹配的方法，其基本思想是把事件流中的事件实例缓存到有序事件列表上，对前期部分事件流片段进行数据采样，计算各事件列表上缓存事件实例的数量，利用数量的多少作为后期选择事件匹配处理顺序的依据。再对列表上的事件实例执行查询匹配操作，其中包含确定最优的起始序列、选择合适匹配顺序并在其余事件列表中校验满足的事件实例，再组成复杂事件候选结果，最终通过进一步的属性验证得到完全正确的复杂事件匹配结果。本文所提方法的主要处理框架如图3所示。

3.1 事件缓存

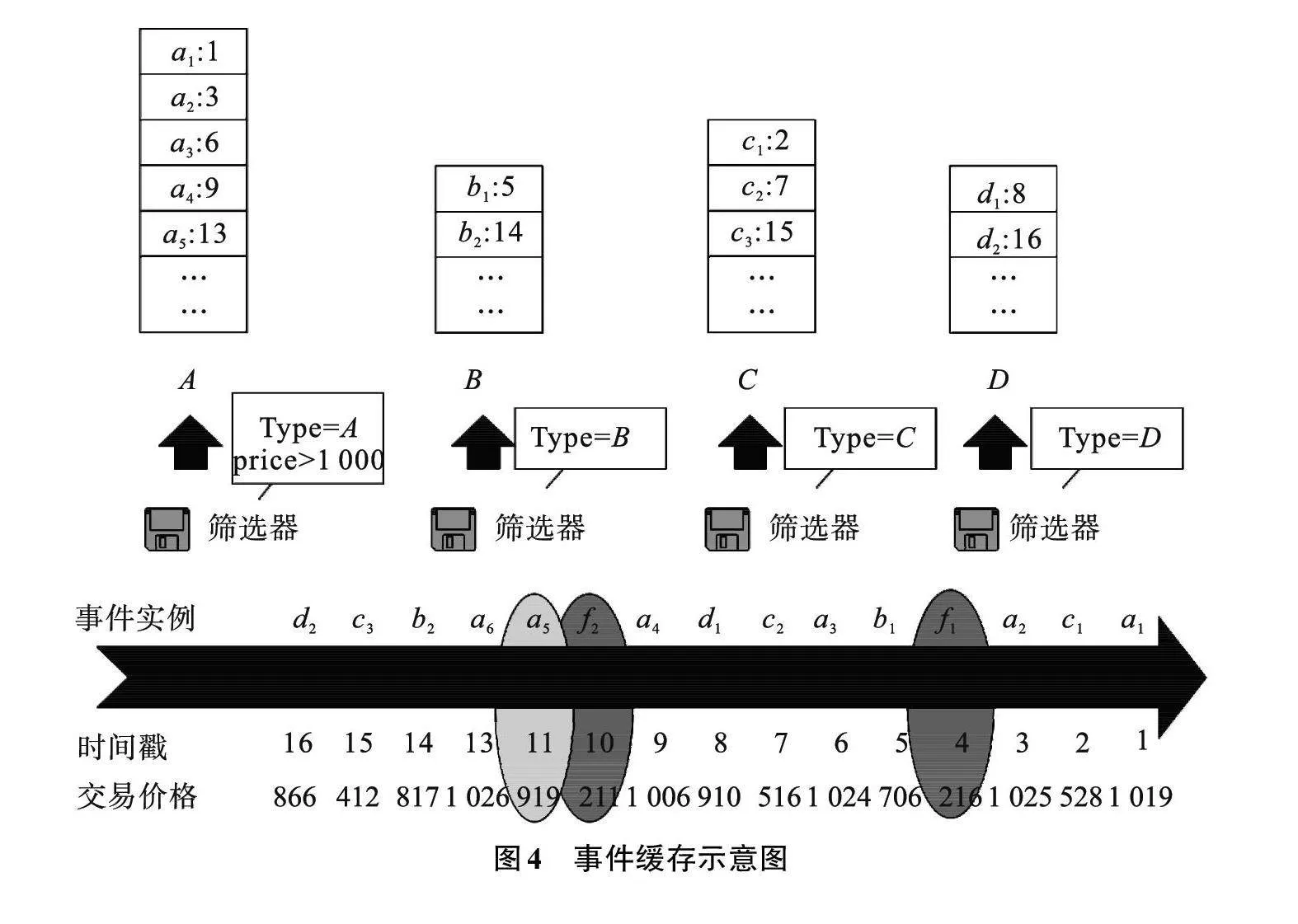
事件缓存的目的是将事件流上的事件实例按照查询模式中的目标序列形式缓存到相对应的有序列表中。给定查询模式Q，其PATTERN目标序列形式为（E1，E2，…，Eh），为目标序列中每个元素Ei对应的事件类型创建相应的缓冲筛选器，进而利用筛选器将事件流上的事件实例缓存到相应的有序缓冲区I（Ei）当中。

查询模式中的所有约束条件都应放在属性验证步骤中进行校验，然而这种方式明显会使查询匹配过程中保留大量无效的中间结果，造成时间及空间上的浪费。事实上有些约束条件可以更早地执行判断。因此，本文将WHERE子句的约束条件分为两大类，一类是事件实例属性与常量间的比较条件，本文称为常量约束；另一类是不同事件实例之间的属性比较，称为关联约束。例如，在例1当中，WHERE子句的条件a.pricegt;x，由于x为用户给定的常量值，该条件即为一个常量约束。对于条件a.pricegt;b.price，其中a与b均为事件实例，该条件即为一个关联约束。常量约束仅作用于单一的事件类型，而事件缓冲筛选器也仅作用于单一的事件类型。因此，可以考虑将常量约束的校验放到事件缓存步骤相应的缓冲筛选器中。这种方式会预先筛选掉事件流上不满足这些常量约束的事件实例，避免其进入缓冲区，减少了事件缓存与查询过滤步骤产生的中间结果，从而提高查询处理效率。

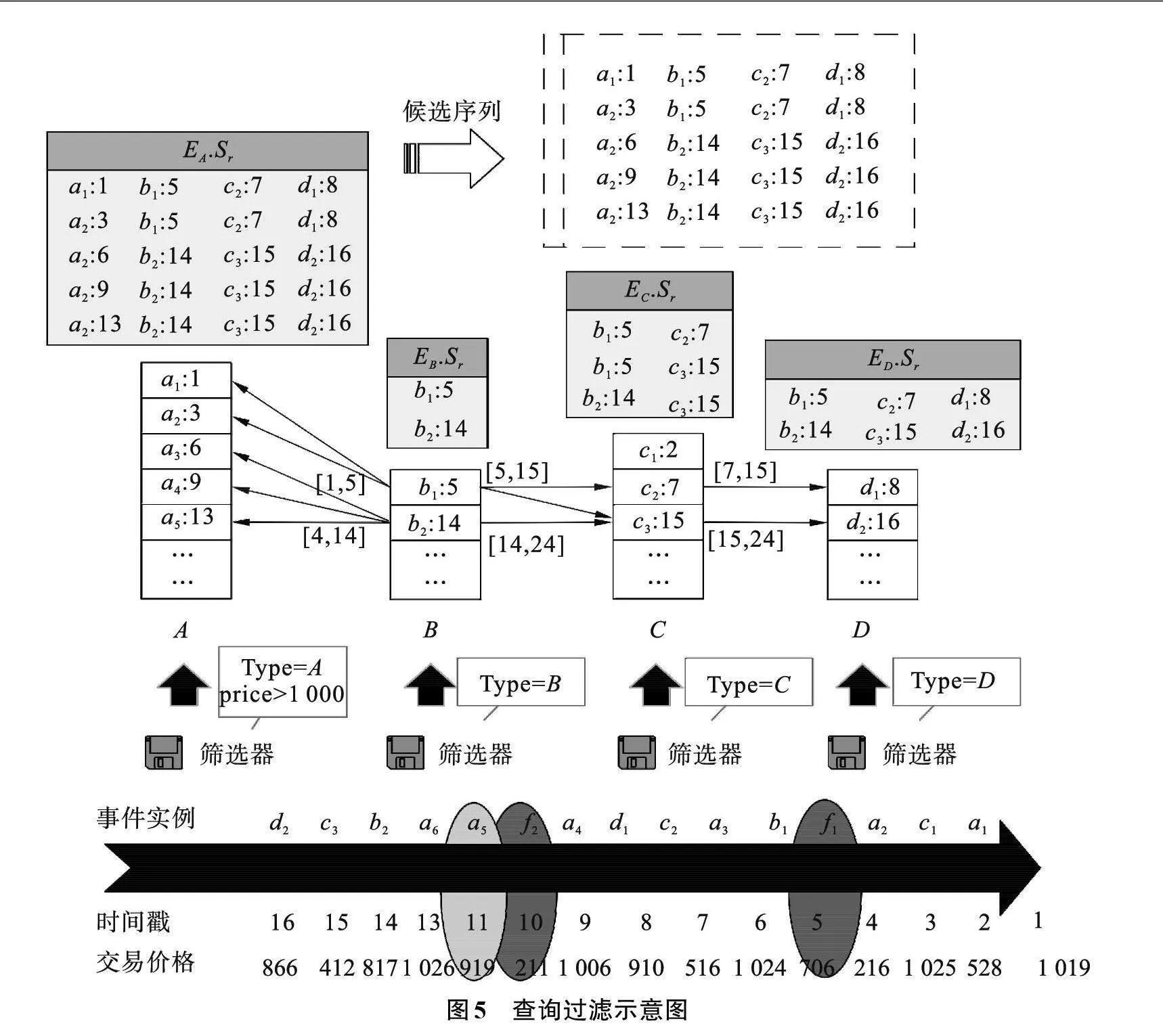
例2" 结合前文图1所示的事件流S以及例1给出的查询模式Q进行事件缓存，如图4所示。按照查询模式中目标序列形式添加筛选器，需构建4个有序事件列表，即缓冲区分别为I（A）、I（B）、I（C）与I（D）。与查询模式无关的事件类型会被过滤掉，如事件f1、 f2。同时筛选器中添加常量约束条件，不满足常量约束a.pricegt;x （设x值为1 000）的事件实例也会被过滤掉，如a5。

3.2 数据采样

数据采样的目的是确定更优的匹配处理顺序，使用更少的匹配次数获得复杂事件匹配结果。在目标序列形式（E1，E2，…，Eh）相应的有序缓冲区I（Ei）（i∈1，2，…，h）中，对前期来自事件流的部分缓存事件实例进行采样计数，计算各事件列表上缓存事件实例的数量，即有序列表的长度Numi（i∈1，2，…，h），利用各有序缓冲区上事件实例数量的多少作为后期确定最优的起始序列，选择适合匹配顺序的依据。由图4缓存得到的有序列表中的部分事件流片段可知，A事件列表中事件实例很多，而B中的事件实例数量相对较少。显而易见，将B作为查询匹配的起始列表，会产生更少的结果，从而使匹配次数减少。

3.3 查询过滤

经过事件缓存步骤之后，事件流上的事件实例被存储到相应有序缓冲区中，接下来在有序缓冲区上执行的查询过滤则是复杂事件匹配的核心操作，其作用是匹配出满足复杂事件目标序列形式约束（PATTERN子句约束）与时间窗口限制（WITHIN子句约束）的复杂事件候选序列。为了减少开销，提高匹配效率，对中间执行匹配操作的次数越少越好。因此本文采用的方法为利用采样获取各个事件类型中事件实例的多少，选取数量最少的事件列表作为初始事件实例，并通过计算初始事件列表前、后两侧其余事件列表上平均事件实例数量来选择合适的匹配顺序，再基于递归的方法从事件缓冲区中匹配出满足条件的复杂事件候选序列。

3.3.1 确定起始序列

常规的查询匹配方式是在前文给定的相关事件缓冲区中按照查询模式中PATTERN子句目标序列的顺序进行查询匹配，显然当目标序列中第一个事件类型有大量实例被缓存时，这种匹配方式会产生大量的中间查询结果，从而导致匹配次数大量增加，影响了查询匹配效率。为减少查询匹配次数，提高效率，本文选取有序事件列表上事件实例缓存数量最少的事件作为查询的初始事件。

为了确定一个最优的起始事件，选取前文采样中事件实例缓存数量最少Numk对应的事件列表Ek作为查询过滤的起始事件列表，并且在该事件对应的缓冲区I（Ek）上获取初始事件实例em，em为该事件缓冲区上的事件实例。此时，这些初始事件实例仅仅是可能存在的候选序列上的某一个事件实例。针对其余的事件序列，若要查询匹配的可能组成候选序列的事件实例，可采用基于递归的方法，从其余各个事件缓冲区中找到候选序列。对于一个初始事件实例em，当且仅当在剩余的其他类型的有序缓冲区中存在满足时间窗口范围内的事件实例，使得它们能构成的集合满足查询模式目标序列时，以em作为起始事件的事件组合就是一个复杂事件候选序列。本文设计了算法1来实现上述匹配过程。

算法1" 复杂事件候选序列匹配算法StartCEP

输入：查询Q中的目标序列Se，事件实例缓存区I，时间窗口大小tw；

输出：匹配的事件序列集合R。

（1）Ek←采样确定的含有最少事件实例的有序事件列表Se.getSimpleMinEvent（）；

（2）while （em←I（Ek）.nextEvent（）amp;em！=1） do

（3） 通过em创建新集合r；

（4） 将r 加入Ek.Sr中；

（5） MatchSubEvents（Ek，Se，R）；

（6）return R；

算法通过采样确定的含有最少事件实例Numk的有序事件列表Ek，将Ek对应的有序缓冲区I（Ek）作为查询匹配的起始事件列表（第1行），并且逐个校验该事件列表上的事件实例em （第2～5行）。对于每一个事件实例em，算法为其创建一个集合r，用于存储当前序列已确定了的事件实例（即已满足了Q中目标序列约束的事件实例，em作为序列中第一个事件实例，r创建时em已被加入其中）。然后，调用算法VerifyEvents （见3.3.2算法2）来校验在其余事件缓冲区中，是否存在时间窗口范围内的事件实例满足目标序列的约束条件。如果校验成功，则满足的事件实例将作为一个复杂事件候选序列存储到集合R中（第6行）。

3.3.2 获取候选序列

在其他事件有序缓冲区中的验证都可以归结为：在一个时间戳允许范围内，判断事件列表缓冲区上是否有对应的事件实例存在。由于构成候选序列的事件实例存在多个，每个事件实例需利用缓存区判断是否真实存在，本文提出基于递归的方法依次校验剩余的事件实例。与常规方式不同的是，该方法中起始事件不再是目标序列中的第一个事件类型，因此需要以起始事件为起点，向查询模式目标序列前、后两侧其余的事件列表进行校验。

在事件列表上校验事件实例的思路为：以确定的起始事件序列上的各个事件实例为起点，通过查询模式Q中WITHIN子句中的时间窗口大小tw计算出前面或者后面事件实例允许发生的时间戳范围［tx，ty］，然后在对应事件缓冲区中判断［tx，ty］时间戳范围内是否存在事件实例。如果构成候选序列的事件实例均存在，则找到的事件实例可以组合为一个复杂事件实例候选序列。

为了减少匹配次数，考虑以确定的起始事件列表为起点，选取优先向前校验或者优先向后校验中更好的查询匹配顺序。在本文中，通过初始事件列表前、后两侧其余事件列表上平均事件实例数量Num前和Num后的大小来作为优先向前校验或者向后校验的依据。其中Num前表示在事件序列Ek前面的E1～Ek-1个事件序列上，对事件实例采样个数求取平均值，即（Num1+…+Numk-1）/（k-1）。同样的，Num后表示在事件序列Ek后面的Ek+1～Eh个事件序列上，对事件实例采样个数求取平均值，即（Numk+1+…+Numh）/（h-k）。

本文设计了带有选择最优查询匹配顺序的基于递归的优化算法，从事件列表缓冲区中找到候选事件序列，如算法2 所示。

算法2" 候选序列匹配算法VerifyEvents

输入：事件类型Ej，查询Q中的目标序列Se，匹配的事件序列集合R；

输出：无。

（1）if Num前gt;Num后

（2） Ei←Se.getNextEk（Ej） ； //先查询校验Ek后面各个事件列表上的事件实例

（3） for each set r in Ej.Sr do

（4） ［tx，ty］←computeTimeRange（Ei，r） ； //计算后面时间戳允许的范围

（5） if Ei.op_type=序列操作 then

（6） for each event ei in I（Ei） s.t. ei.timestamp∈［tx，ty］ do

（7） 通过r创建新集合r'；

（8） 将ei 加入r' 中；

（9） 将r' 加入Ei.Sr中；

（10） else if Ei.op_type=闭包操作 then

（11） k←Ei上的闭包参数；

（12） count←0 ； S'←Ø ；

（13） for each event ei in I（Ei） s.t. ei.timestamp∈［tx，ty］ do

（14） count ++；

（15） add ei to S'；

（16） if count≥k then

（17） 通过r创建新集合r'；

（18） 将 S' 中所有事件实例加入r' 中；

（19） 将r' 加入Ei. Sr中；

（20） else if Ei.op_type=否定操作 then

（21） for each event ei in I（Ei） s.t. ei.timestamp∈［tx，ty］ do

（22） 将ei的时间戳设置成r的时间窗口的终止时间；

（23） break； //（5）～（13）行为判别各个事件列表操作类型，执行校验操作

（24） if Ei ！= Se.lastEvent（） then

（25） MatchSubEvents（Ei，Se后，R）；

（26） else

（27） Ei←Se.getPrevEk （Ej） ； //再去查询校验Ek前面各个事件列表上的事件实例

（28） for each set r in Ej.Sr do

（29） ［tx，ty］←computeTimeRange（r，Ei） ； //计算前面时间戳允许的范围

（30） 执行（5）～（13）行的校验操作；

（31） if Ei ！= Se.firstEvent（） then

（32） MatchSubEvents（Ei，Se前，R）；

（33） else

（34） for each set r in Ei.Sr do

（35） 将r中事件序列加入R中；

（36） Ei.Sr←Ø；

（37） return R；

（38） else Num前lt;Num后

（39） Ei←Se.getPrevEk （Ej） ； //先查询校验Ek前面各个事件列表上的事件实例

（40） for each set r in Ej.Sr do

（41） ［tx，ty］←computeTimeRange（r，Ei） ； //计算前面时间戳允许的范围

（42） 执行（5）～（13）行的校验操作；

（43） if Ei ！= Se.firstEvent（） then

（44） MatchSubEvents（Ei，Se前，R）；

（45） else

（46） Ei←Se.getNextEk （Ej） ； //再查询校验Ek后面各个事件列表上的事件实例

（47） for each set r in Ej.Sr do

（48） ［tx，ty］←computeTimeRange（Ei，r） ； //计算后面时间戳允许的范围

（49） 执行（5）～（13）行的校验操作；

（50） if Ei ！= Se.lastEvent（） then

（51） MatchSubEvents（Ei，Se后，R）；

（52） else

（53） for each set r in Ei.Sr do

（54） 将r中事件序列加入R中；

（55） Ei.Sr←Ø；

（56） return R；

算法2有3个输入参数，其中Ej表示目标序列上当前已校验成功的事件类型（即对应的事件实例缓冲区上具有满足约束条件的事件实例），Se为查询Q中的目标序列，R用于存储递归校验后得到的复杂事件序列结果。算法2先计算初始事件列表前侧的其余事件列表上平均事件实例数量Num前和后侧的其余事件列表上平均事件实例数量Num后的大小，选择事件实例数量小的一侧优先校验。如果Num前gt;Num后，则优先校验起始序列Ek后面的各个事件列表上的事件实例（第1～37行）。当Ek后面所有事件列表均校验完毕，即Ei为最后一个事件列表时，再对Ek前面的各事件列表进行校验，直至校验到第一个事件列表，即对所有事件列表校验完成，则当前获得的Ej.Sr中任意一个集合都表示一个满足约束的候选序列，并将其加入到R中。同理，如果Num前lt;Num后，则优先校验起始序列Ek前面的各个事件列表上的事件实例（第37～56行）。对于Ej.Sr中存储的每一个集合r （表示当前已经部分满足目标序列约束的事件实例集合），根据r中的事件实例计算出Ei类型的事件实例允许前面或者后面出现的时间戳范围［tx，ty］。

由于Ei的序列操作类型不同，在其对应的事件实例缓冲区上进行的校验操作也不同，因此算法2需分别对Ei的3种序列操作类型进行讨论：

当Ei的序列操作类型为顺序操作时，算法在Ei对应的事件缓冲区I（Ei）上找到所有满足时间戳范围［tx，ty］的事件实例ei。由于每一个加入的实例ei，都表示一种新的部分匹配上的目标序列，因此需将ei加入到r中，并创建得到新的集合r'。r'再存入Ei.Sr中，用于下轮递归调用时进行校验。

当Ei的序列操作类型为闭包操作时，需先获取闭包参数k值。然后设置一个临时变量count，对满足时间戳范围的事件实例进行计数。同理，算法2需在I（Ei）上找到满足时间戳范围的事件实例。不同于处理顺序操作，仅当实例的个数大于闭包参数值k时，才创建新的集合r'，用于表示新的部分匹配序列。

当Ei的序列操作类型为否定操作时，其处理方法不同于顺序操作与闭包操作。由于复杂事件序列不能包含否定操作下的事件实例，目标序列无法跨过否定操作的事件实例。基于该性质，复杂事件匹配过程不能包含否定操作下的事件实例。算法2利用出现在时间戳范围内实例的时间戳更新当前部分匹配集合r的终止时间，从而保证匹配得到的目标序列所在时间戳范围不包含否定的事件实例。

例3" 本例沿用例2中股票交易数据缓存到有序缓冲区的数据，由前文对事件流片段的采样可知，B中事件实例的数量较少，因此选择以B事件列表作为起始列表。同时在该采样片段中B事件列表后面的C、D列表中，事件实例数量分别为NumC=3、NumD=2，而前面A事件列表中事件实例数量NumA=5，因此优先选择向后校验会产生更少的匹配次数。以b1：5为例，其向后校验I（C）上的事件实例，计算其后允许的时间戳范围为［5，15］，因此在I（C）上可以找到c2：7和c3：15两个实例，同理递归校验在I（D）上的事件实例。当判断I（D）是向后最后一个事件列表时，则向后校验结束，需再向前校验起始列表前面的事件实例，即I（A）上可满足时间戳范围的事件实例。此时判断I（A）为向前第一个事件列表，可以确定向前校验已经完成，此时将当前存储的事件实例集合即复杂事件候选序列输出，如图5中右侧给出的5个候选序列结果。

3.4 属性验证

由于查询模式WHERE子句中的关联约束难以在事件缓存和查询过滤中做校验处理，所以在这两个步骤之后得到的复杂事件候选序列并不能保证完全符合查询模式的约束。因此，系统最后一步属性验证的目的是进一步检查查询模式中的关联约束，筛除不满足该约束的候选序列。

针对查询过滤产生的复杂事件候选序列，结果验证步骤则需要在其上添加筛选器，将筛选条件设置为查询模式中的关联约束。复杂事件候选序列通过带有关联约束的筛选器，筛选器检查其属性是否均满足设定的关联约束条件，不满足关联约束的候选序列会被筛除掉，满足的即为正确的复杂事件结果。

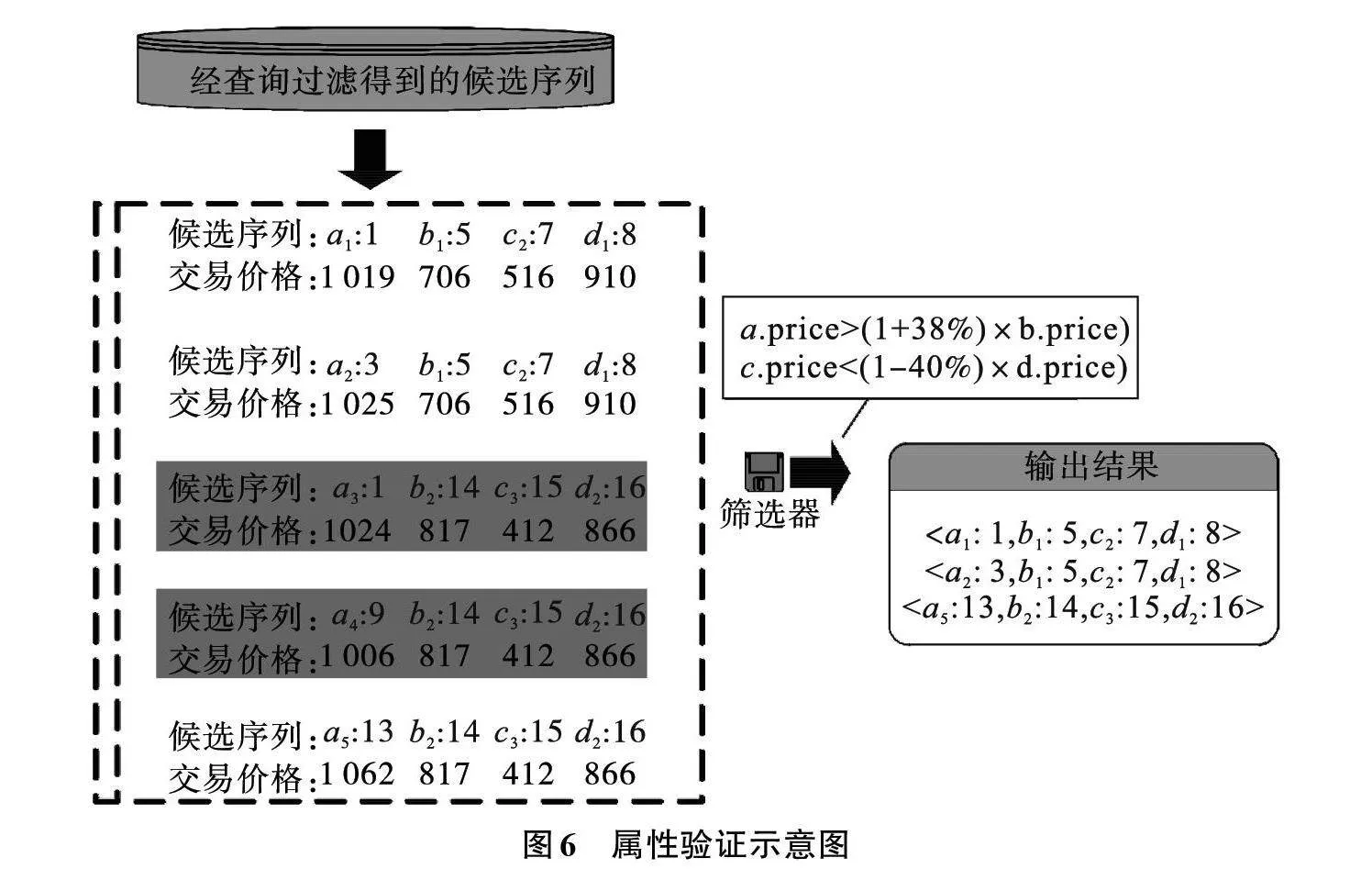
例4" 例3在经过如图4的查询过滤处理之后，得到如图5所示部分复杂事件候选序列。针对这些复杂事件候选序列添加查询Q中的关联约束作为验证条件进行进一步的属性验证，（设y值为38，z值为40）。图6中阴影部分的两个候选序列的并不满足a.pricegt;（1+38%）*b.price这一关联约束条件，所以它并不是正确的复杂事件结果，因此这两个候选序列会被过滤掉。

4 实验结果与分析

通过实验对比，对本文提出的在有序事件列表上选择最佳匹配顺序进行递归遍历的复杂事件匹配方法的有效性进行了分析和验证。采用Java实现了优化方法的编写。本节将从多个维度对实验结果进行分析说明，并通过性能对比证明其有效性。

4.1 实验设置

本文优化方法将与目前比较流行的SASE方法和Siddhi方法进行对比实验，对本文提出的在有序事件列表上选择最佳匹配顺序进行递归遍历的复杂事件匹配方法记为OptiSeq。

实验数据集采用SASE股票模拟数据事件流生成器生成的股票交易模拟数据，该数据集包含100万个股票交易数据信息，其中带有时间戳、交易价格、交易数量等属性。在实验过程中，为保证实验的可比性，在各个实验中将复杂事件查询做一致性处理，即目标序列相同，事件类型个数相同，属性约束相同，事件窗口大小相同。在本节实验中将复杂事件查询匹配结果的处理时间作为实验的性能指标进行评估。

以下所有的实验均是在实验环境配置如表1所示的服务器上进行。

4.2 实验结果与分析

为证明本文提出算法的有效性和高效性，首先对所提出的OptiSeq算法与SASE、Siddhi方法在同一查询模式下进行总体性能对比实验，其次又检验了不同影响因素，如复杂事件类型个数、时间窗口大小在各个方法间性能的比较。设置以下3个实验进行对比测试。

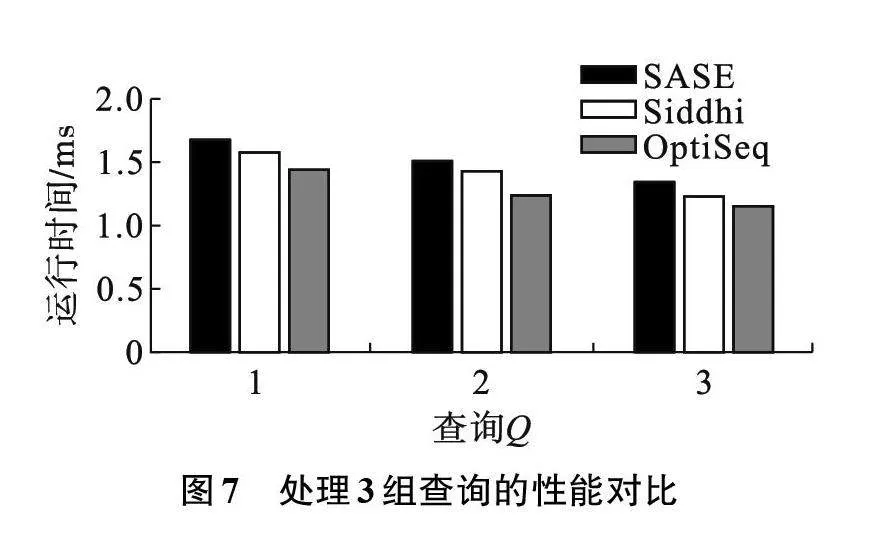
实验1：在数据集上对3种方法各测试了3组查询，保证每组查询中这些复杂事件查询的序列长度为4，同时为了排除时间窗口约束的影响，将时间窗口统一为2 min，对应的值则是该组查询的运行时间。实验结果如图7所示，其中OptiSeq算法比SASE算法的处理时间平均降低了15.46%，比Siddhi方法降低了9.41%。

实验2：评估目标序列长度对运行时间的影响。为排除其他因素的影响，在实验2中设置复杂事件查询模式均在同一时间窗口为2 min时，改变查询模式中事件类型个数，分别由3个递增到6个事件类型时的4组评估结果。将3种方法对复杂事件处理结果所用的运行时间作为评估指标，对比实验结果如图8所示，其中OptiSeq算法比SASE算法的处理时间平均降低了21.19%，比Siddhi方法降低了18.55%。并且通过图8可以发现，随着目标序列长度的增加，OptiSeq比另外两个方法的性能提升更大。

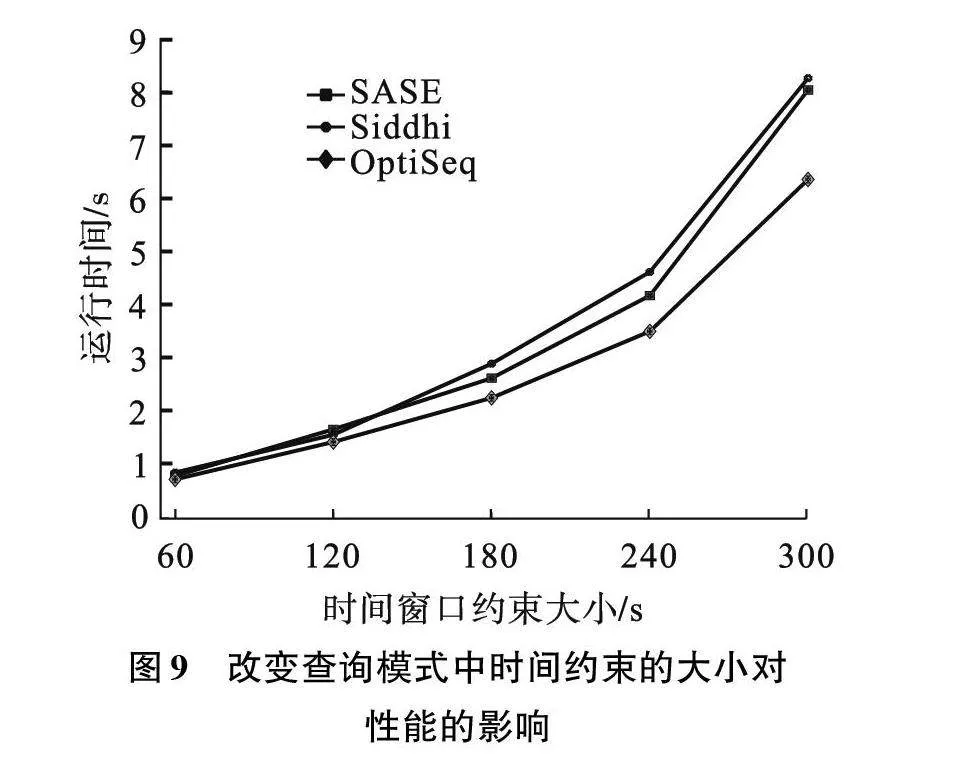
实验3：评估时间窗口约束对运行时间的影响。在实验3中设置查询中的目标序列长度为4个，即PATTERN（A；B；C；D），同时给定每组查询相同的属性约束条件，分别测试了时间窗口约束从1～5 min的5组评估结果。如图9所示，在不同的时间窗口约束下，OptiSeq的处理性能优于其余两个方法。实验对比结果中，当时间窗口为240 s时，OptiSeq的处理性能比SASE提升了16.02%，比Siddhi提升了22.93%。

5 结论

本文提出了一种新型的利用有序列表缓存事件实例的结构，通过该结构避免了临时匹配的集中式存储及使用。提出了通过比较列表中事件实例的多少来选择最优匹配顺序进行过滤查询的方法，以及候选序列匹配算法StartCEP和候选序列匹配算法VerifyEvents。通过这两个算法，能够在减少中间匹配结果和匹配次数的情况下，保证复杂事件处理匹配结果的正确性和完整性。在模拟数据集和真实数据集上对优化方法的性能进行对比实验和分析，实验结果表明，本文提出的在有序事件列表上选择最优匹配顺序进行递归遍历的复杂事件匹配方法，在处理查询模式中事件类型较多或者时间窗口约束较大的情况下，都能够有效得到复杂事件处理结果，并且在处理性能上可以更有效地避免大量重复计算，减少处理时间。

参考文献（References）：

［1］ 产院东，郭乔进，梁中岩，等.规则引擎发展综述［J］.信息化研究，2021，47（2）：1-6.

［2］ 乔雅正，程良伦，王涛，等. 地铁列车环境中多依赖复杂事件处理研究［J］. 计算机应用研究，2019，36（8）： 2355-2358，2367.

［3］ Rahmani A M，Babaei Z，Souri A.Event-driven IoT architecture for data analysis of reliable healthcare application using complex event processing［J］.Cluster Computing，2021，24（2）：1347-1360.

［4］ 王亚辉，郑联语，樊伟. 云架构下基于标准语义模型和复杂事件处理的制造车间数据采集与融合［J］. 计算机集成制造系统，2019，25（12）： 3103-3115.

［5］ 鲍军鹏，左宏良，杨科. 基于事件流的航天大数据复杂事件挖掘框架［C］//2018软件定义卫星高峰论坛摘要集.西安：西安电子科技大学出版社，2018： 74-80.

［6］ Agrawal J，Diao Y L，Gyllstrom D，et al.Efficient pattern matching over event streams［C］//Procee dings of the 2008 ACM SIGMOD International Conference on Management of Data.Vancouver，Canada：ACM，2008：147-160.

［7］ Wu E，Diao Y L，Rizvi S.High-performance complex event processing over streams［C］//Proceedings of the 2006 ACM SIGMOD International Conference on Management of Data.Chicago，USA：ACM，2006：407-418.

［8］ Mei Y，Madden S.ZStream：a cost-based query processor for adaptively detecting composite events［C］//Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data.New York，USA：ACM，2009：193-206.

［9］ Suhothayan S， Kasun G， Isaure L N， et al. Siddhi： a second look at complex event processing architectures［C］//Proceedings of the 2011 ACM SC Workshop on Gateway Computing Environments， Seattle， USA：ACM， 2011：43-50.

［10］ Giatrakos N，Alevizos E，Artkis A，et al.Complex event recognition in the big data era： a survey［J］. The VLDB Journal，2020： 29（1）： 313-352

［11］ Diao Y L，Immerman N，Gyllstrom D. Sase+：an agile language for kleene closure over event streams［J］. UMass Technical Report，2007， 7（3）： 1-13.

［12］ Demers A，Gehrke J，Hong M S，et al．Towards expressive publish/subscribe systems［M］//Lecture Notes in Computer Science．Berlin：Springer-Verlag，2006：627-644．

［13］ Demers A，Gehrke J，Panda B，et al. Cayuga： a general purpose event monitoring system［C］//Proceedings of the 2007 International Conference on Innovation Database Research.Asilomar，USA：ACM，2007： 412-422.

［14］ 赵润发，娄渊胜，叶枫，等．基于Flink的工业大数据平台研究与应用［J］．计算机工程与设计，2022，43（3）886-894.

［15］ Dousson C．Extending and unifying chronicle representation with event counters［C］//Proceedings of the 15th European Conference on Artificial Intelligence．New York，USA：ACM，2002：257-261．

［16］ Artikis A，Sergot M，Paliouras G．An event calculus for event recognition［J］．IEEE Transactions on Knowledge and Data Engineering，2015，27（4）：895-908．

［17］ Liu M，Rundensteiner E，Greenfield K，et al．E-Cube：multi-dimensional event sequence analysis using hierarchical pattern query sharing［C］//Proceedings of the 2011 ACM SIGMOD International Conference on Management of Data.New York，USA：ACM，2011：889-900．

［18］ 喻学军，肖蓓. 一种高效的复杂事件处理引擎Esper［J］. 数字技术与应用，2020，38（11）：50-52.

［19］ 郑利强，廖湖声，苏航，等.一种针对正规树模式的复杂事件查询方法［J］.计算机与数字工程， 2018，46（5）：966-971.

［20］ Grea A，Riveros C， Ugarte M.A formal framework for complex event recognition ［J］.ACM Transactions on Database Systems，2021，46（4）：1-49.

（责任编辑：刘划" 英文审校：杜文友）