超高压空气的热物性计算

摘要： 为研究高超声速风洞部件的气动特性，运用空气的亥姆霍兹能状态方程和输运物性方程组，计算超高压工况下空气的热物性参数。将计算结果与美国国家标准与技术研究院（National Institute of Standards and Technology，NIST）数据库的实验数据进行比较，得到相对误差值。结果表明，空气亥姆霍兹能状态方程和输运物性方程组计算得到的空气热物性参数与NIST标准实验数据相比误差较小，可以应用于超高压状态下的空气热物性计算。

关键词： 超高压空气；气动特性分析；空气亥姆霍兹状态方程；热力学参数；输运物性参数

中图分类号： V211.3" " " " 文献标志码： A

doi：10.3969/j.issn.2095-1248.2023.02.003

Thermal properties calculation of hyper-high pressure air

CHEN Kui-da1， XU Rang-shu1， SUN Dan1， XU Long2

（1. College of Aero Engine， Shenyang Aerospace University， Shenyang 110136，China；

2. CNPC Jichai Power Co.，Ltd.，Jinan 250300，China）

Abstract： In order to investigate the aerodynamic characteristics of hypersonic wind tunnel components， the air Helmholtz energy equation of state and transport physical property equations of air were used to calculate the thermal physical property parameters of air under hyper-high pressure conditions. The relative error values were obtained by comparing the calculated results with experimental data from the National Institute of Standards and Technology （NIST） database. The results show that the error of the air thermal property parameters obtained from the Helmholtz energy equation of state and the transport physical property equations is smaller than the NIST standard experimental data， which can be applied to the calculation of air thermal property under hyper-high pressure.

Key words： hyper-high pressure air；aerodynamic characteristic analysis；air Helmholtz energy equation of state；thermodynamic parameters；transport properties parameters

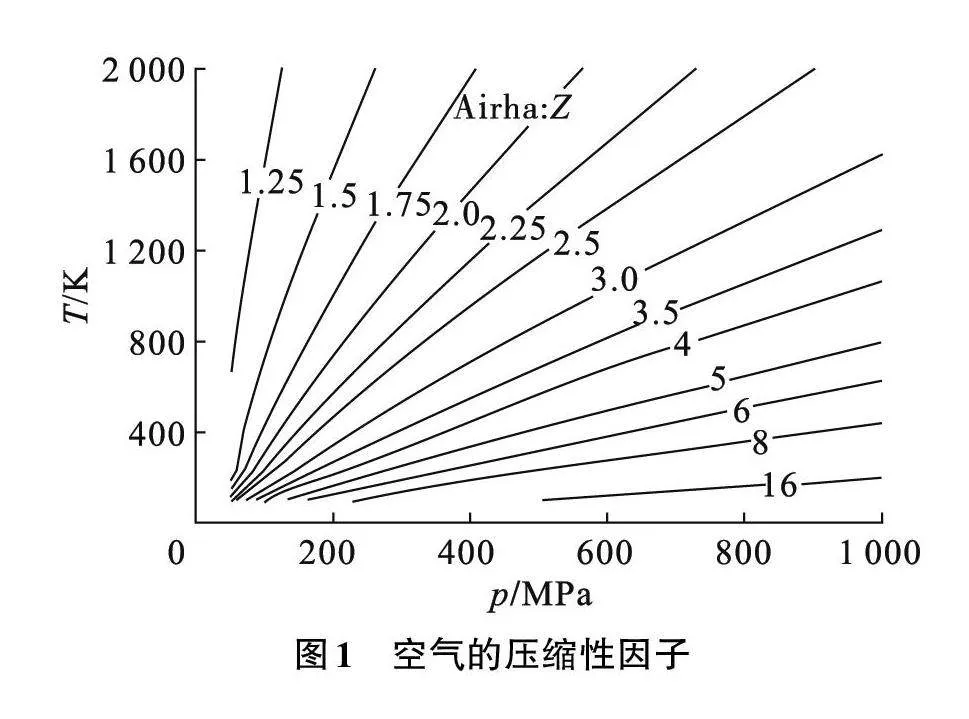
近年来，随着高超声速飞行器的兴起，对高超声速风洞的研制提出更多需求和更高的指标［1］。高超声速风洞的超高压驱动系统通过加压装置和喷管向风洞提供达到超高压状态的工作介质。由于需要模拟高超声速飞行时的气动情况和热力学条件，驱动气源往往具有很高的总温。在超高压和高温条件下，空气的热力学特性与理想状态下有较大的偏差，空气状态远远偏离理想气体方程，热力学参数也与量热完全气体偏离，具有明显的实际气体特征。在常温范围和200～300 MPa的压力下，空气的压缩性因子可以达到3～4，在更大范围温度和压力下空气的压缩性因子如图1所示。

以往气动特性分析领域的研究大多采用范德瓦尔斯方程、Redlich-Kwong方程和Span方程作为气体的状态方程［2］。其适用条件仅为常压和高压，无法满足超高压工况计算的要求。目前，超高压领域的相关研究大多关注氮气、氩气、氙气等稳定气体在超高压工况下的热力学参数计算［3-5］，在一定程度上，其研究的方法和思路也为空气的热物性研究提供参考。关于空气的研究，Cottrell等［6］提出一系列适用于密度接近固体密度和远高于临界温度气体的状态方程。但由于其理论方法和状态方程较为复杂，不便于运用，董赛鹰等［7］、芶清泉等［8］对其进行简化，提出一个比较简单实用的高温高压状态方程，用来计算高温高压气体的热力学函数与性质。由于该公式的压力适用范围受限，且实验数据主要来自氩气，同样无法应用于求解超高压状态下空气热物性。超高压状态下，随着气体和气液两相的转变，以上的气体状态方程及吉布斯能量方程关于介质相态转变的计算公式并不连续［9］，故亟需一套适用范围更广、计算精度更高的状态方程。

区别于以往将空气假设为氮、氧、氩的混合物，再根据这3种物质各自的状态方程计算纯质的物性，然后通过热力学上的混合法则，求取气体混合物性质的方法，Lemmon等［10］根据实验得到的压力、温度、密度、比热容、声速和气液平衡数据，提出标准干燥空气的热力学参数公式。该公式适用于温度从气泡点曲线上的冷凝点（59.75 K）到2 000 K，压力高达2 000 MPa的液态、气态和超临界态的空气。由于缺乏873 K和70 MPa以上空气的可靠实验数据，该研究又根据该地区的氮气数据预估空气热力学参数，以扩大公式的有效范围。除了标准干燥空气的状态方程外，Lemmon等还提出一种以亥姆霍兹能状态方程方程为基础的混合物热力学参数计算模型。该模型能够计算含氮、氩和氧的混合物的热力学性质，适用于温度从气泡点曲线上的冷凝点（59.75 K）到1 000 K，压力高达100 MPa的情况。混合物的亥姆霍兹能是理想气体能量、实际气体能量和混合物能量的总和。混合物能量由另一个广义方程给出，自变量是无量纲密度和无量纲温度。该模型适用于本研究中所有的混合物，也可用于计算各种组分的混合物的热力学性质，包括露点、泡点和临界点，契合每种已公布的最精确的纯流体状态方程。混合物模型中密度、声速、比热容的计算误差分别为0.1%、0.2%、1%。计算得到的露点和泡点压力一般精确达到1%以内。孟令军等［11］的研究表明其计算精度高于Bender状态方程，但文献［11］针对超高压工况的计算存在空缺，有待补充。

对于气体的输运物性，即动力黏度和导热系数，目前的研究主要集中于能源领域的非极性有机化合物，如Stiel-Thodos法［12］，但该经验公式并不适用于氢气、氧气和氦气等极性气体。Lemmon等［13］采用研究空气状态方程的经验方法，将空气视为伪纯流体，并使用一个简化的交叉方程来模拟热导率临界增强的行为，提出一套输运物性参数计算公式。该方程是将稀释气体和热导率临界增强的理论模型结合，引入分子间相互作用产生的剩余流体的经验方程。稀释气体的方程参考查普曼-恩斯考克理论，将该理论中的碰撞积分拟合到实验数据中。临界增强采用简化的Olchowy等［14］提出的交叉模型。剩余流体的经验方程与典型的亥姆霍兹能量状态方程中使用的参数相似。各方程的项数被保持在最低限度，使得方程可用于求解低温、高温、高压和高密度的气动参数。最终方程的推导采用研究空气状态方程时所使用的非线性拟合法。与现有的实验数据进行比较，氮气和氩气的不确定度一般在2%以内，氧气和空气的不确定度在5%以内。除了在不确定度较高的临界区域，该方程对所有液体和蒸汽状态都有效，且具备较高的精度。

本文将采用空气亥姆霍兹能状态方程和输运物性方程计算包含100～2 000 K、50～1 000 MPa范围内的空气热力学参数。每个参数选用9 216组数据，并与美国国家标准与技术研究院数据库的实验数据进行比对，用相对误差和平均相对误差来评估该气动特性方程组的适用性。

1 空气亥姆霍兹能状态方程和输运物性方程

1.1 空气亥姆霍兹能状态方程

空气亥姆霍兹能状态方程自变量为无量纲密度和无量纲温度。该方程主要由理想气体亥姆霍兹能和实际气体亥姆霍兹能的校正因子组成，其基本形式如式（1）所示

α（δ，τ）=α（ρ，τ）/RT=α^0 （δ，τ）+α^r （δ，τ） （1）

其中：

（α^0 （δ，τ）=lnδ+∑_（i=1）^5▒〖N_i τ^（i-4） 〗+N_6 τ^1.5+@N_7 lnτ+N_8 ln[1-exp（-N_11 τ） ]+@N_9 ln[1-exp（-N_12 τ） ]+@N_10 ln[2/3+exp（N_13 τ） ] ） （2）

α^r （δ，τ）=∑_（k=1）^10▒〖N_k δ^（i_k ） τ^（j_k ） 〗+∑_（k=11）^19▒〖N_k δ^（i_k ） τ^（j_k ） exp（-δ^（l_k ） ） 〗 （3）

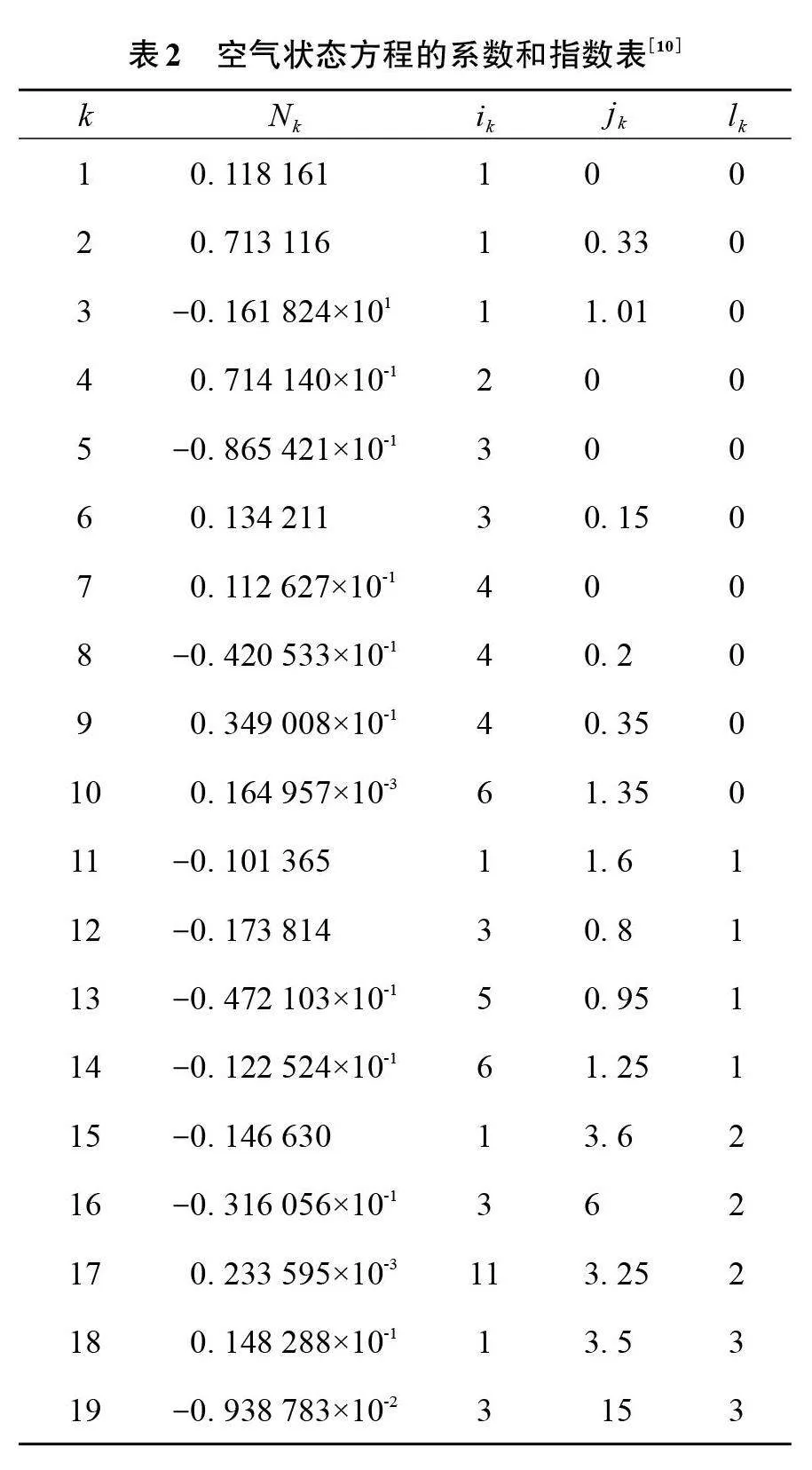
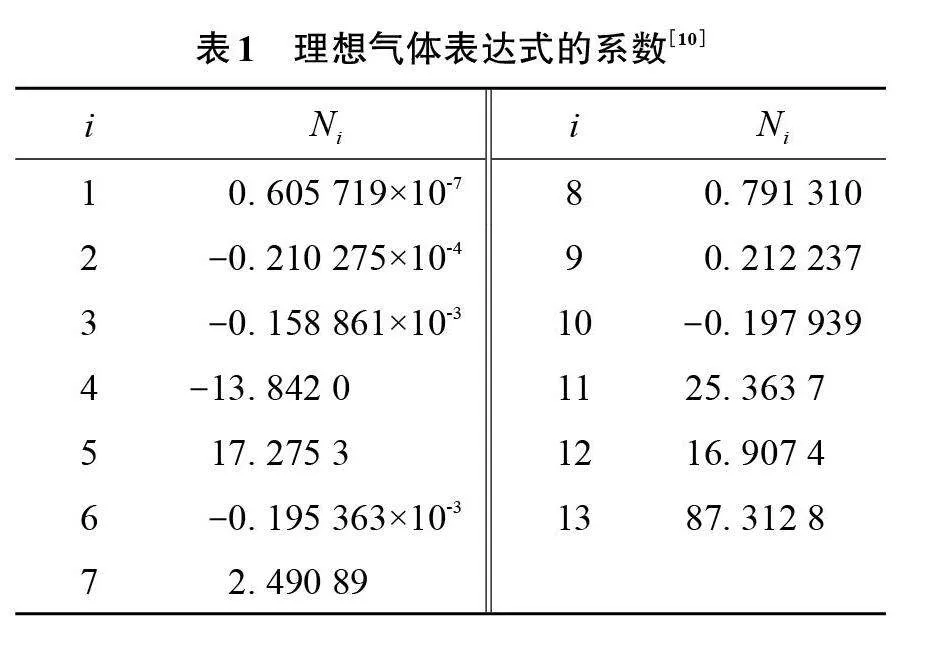
式中：α为空气亥姆霍兹能；α0为理想气体亥姆霍兹能；α^r为实际气体亥姆霍兹能的校正因子；δ=ρ/ρj为无量纲密度；τ=Tj/T为无量纲温度的倒数值；ρj和Tj为空气在最大冷凝温度表中对应的密度和温度，分别为10.447 7 mol/dm3和132.631 2 K。Ni、Nk、ik、jk的取值如表1和表2所示。

1.2 输运物性方程

输运物性方程包含动力黏度方程和导热系数方程。Lemmon等研究该方程的思路参考空气亥姆霍兹能状态方程，故该方程的形式与状态方程类似，均以无量纲密度和无量纲温度为自变量。

1.2.1 动力黏度

动力黏度公式主要由稀释气体动力黏度和剩余流体动力黏度组成，其基本形式如式（4）所示

其中

η^0 （T）=（0.026 695 8√MT）/（σ^2 Ω（T^* ） ） （5）

Ω（T^* ）=exp（∑_（i=1）^n▒〖b_i [ln（T^* ） ]^i 〗） （6）

η^r （τ，δ）=∑_（i=1）^n▒〖N_i τ^（t_i ） δ^（d_i ） exp（-γ_i δ^（l_i ） ） 〗 （7）

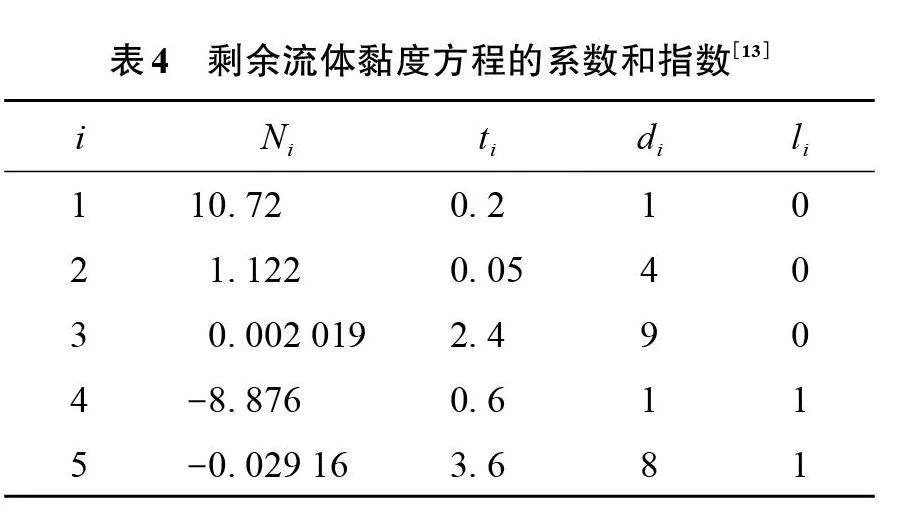
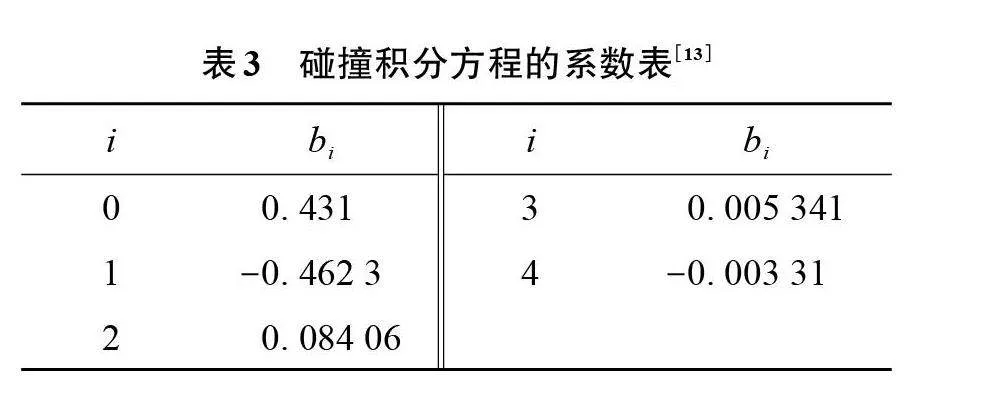
式中：η为动力黏度；η0为稀释气体的动力黏度；ηr为剩余流体的动力黏度；δ、τ定义与上述的定义相同；σ为伦纳德-琼斯尺寸参数，对于空气来说，该值取0.36 nm；Ω为碰撞积分；bi、i的取值如表3所示；T*=T/（ε/k） 为伦纳德-琼斯能量势，对于空气来说，ε/k的取值为103.3；bi的参数如表3所示。当li为0时，γi为0；li不为0时，γi为1。Ni、 ti、 di、 li的取值如表4所示。

1.2.2 导热系数

导热系数主要由稀释气体导热系数、剩余气体导热系数和临界增强导热系数组成，其基本形式如式（8）所示

λ=λ^0 （T）+λ^r （τ，δ）+λ^c （τ，δ） （8）

其中

λ^0 （T）=N_1 （（η^0 （T））/（1μPa⋅s））+N_2 τ^（t_2 ）+N_3 τ^（t_3 ） （9）

λ^r （τ，δ）=∑_（i=4）^n▒〖N_i τ^（t_i ） δ^（d_i ） exp（-γ_i δ^（l_i ） ） 〗 （10）

λ^c （τ，δ）=ρc_p （（kR_0 T）/6πξη（T，ρ） ）（〖Ω┴˜〗┴（" ）-〖Ω┴˜〗┴（" ）_0 ） （11）

式中：λ为导热系数；λ0为稀释气体的导热系数；λr为剩余气体导热系数；λc为临界增强导热系数；δ、τ、η0、γi的定义与1.1节的定义相同；Ni、ti、di、li的取值如表5所示；k为玻尔兹曼常数（1.380 658×10-23 J/K）；理论常数R0=1.01。

另外，使用Olchowy和Sengers的导热系数临界增强模型［14］计算临界区的流体性质，该模型的公式如式（12）、（14）所示

式中：理论常数v=0.63、γ=1.241 5；流体特定的参数qD=0.31、ξ0=0.11、Γ=0.055； Tref为温度高于临界温度时的参考温度，在该计算中取值为临界温度的2倍，即265.2624 K。当式（14）中方括号内的计算值为负数或0时，λc为0。

2 热物性标准数据和误差计算

本文将采用NIST发布的空气热物性数据作为计算的热力学和输运物性参数的对照标准数据。具体的物性数据将通过CoolProp软件［15］获取。该软件属于开源软件，能直接在EXCEL中通过程序指令进行操作，比REFPROP软件操作方便。

本文使用相对误差和平均相对误差来比较描述计算结果与NIST数据库的偏离情况，平均相对误差公式如式（16）所示

AARE= 1/n ∑_（j=1）^n▒|（Φ_（cald，j）-Φ_（real，j））/Φ_（real，j） | ×100% （16）

式中：Φcald，j为第j个数据的物性参数计算值；Φreal，j为NIST数据库的对应参数值；n为计算的参数个数。

3 空气热力参数计算及误差

本节将使用空气亥姆霍兹能状态方程和输运物性方程计算在100～2 000 K、50～1 000 MPa范围内的空气热力学参数，其中温度以20 K为间隔设置观测点，压力以10 MPa为间隔设置观测点，每个参数各计算9 216组数据，并分析计算结果的相对误差和平均相对误差。

3.1 密度

根据第1节介绍的空气亥姆霍兹能状态方程可以推导出空气的密度公式如式（17）所示

Z=p/ρRT=1+δ（（∂α^r）/∂δ）_τ （17）

如图2所示，以等密度线表示温度T为50～2 000 K、压力p为100～1 000 MPa时空气密度与压力和温度的分布情况。两组曲线分别为空气亥姆霍兹能状态方程计算的结果和NIST数据库的结果。当压力小于150 MPa或者温度小于400 K时，两线的重合情况最为理想，计算误差较小。随着温度和压力的升高，两线逐渐偏离，尤其在压力超过400 MPa以后，误差愈发明显。在9 216组数据中有2 990组误差值低于5%。密度的平均相对误差为5.73%。

图3中，选取100～1 000 MPa范围内的6组压力值，绘制密度相对误差与温度的关系图。6组压力的密度平均误差分别为4.79%、5.80%、6.24%、6.47%、6.55%、6.61%。密度的相对误差基本都在10%以内，且误差值随着温度的升高而下降。

3.2 焓

计算空气焓的方程由空气亥姆霍兹能状态方程推导得到，一般式如式（18）所示

h/RT=τ[（（∂α^0）/∂τ）_δ+δ（（∂α^r）/∂τ）_δ ]+δ（（∂α^r）/∂δ）_τ+1" （18）

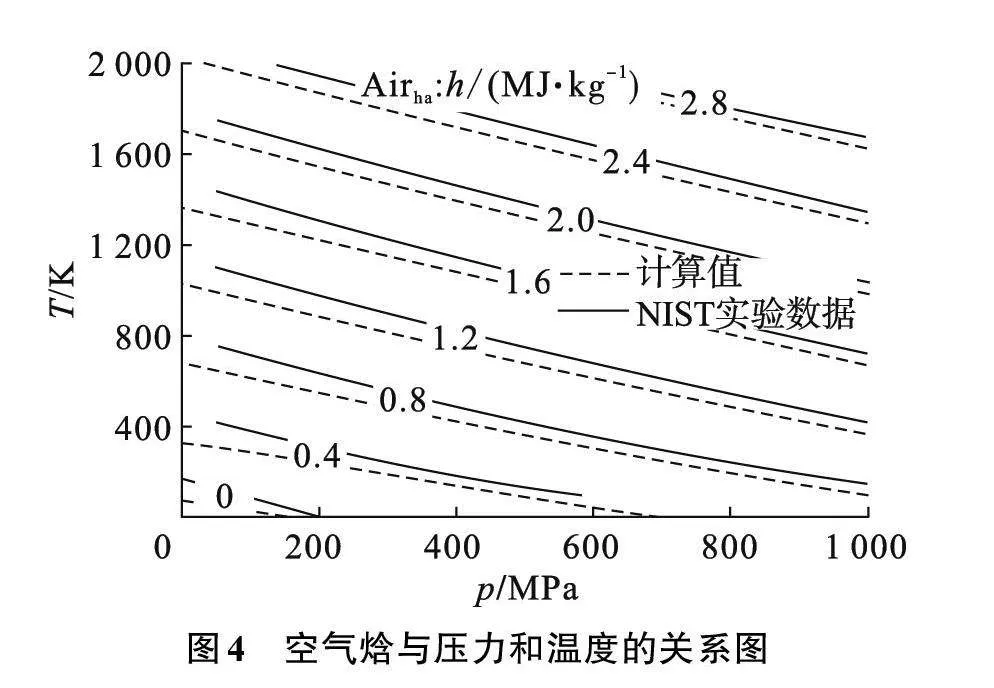
如图4所示，以等焓值线表示温度T为50～2 000 K、压力p为100～1 000 MPa时空气焓值与压力和温度的分布情况。空气亥姆霍兹能状态方程计算的结果和NIST数据库的结果有较为明显的偏差，虽然不完全重合，但处于一个相对平行的关系，说明计算值的变化规律与数据库相吻合。而且随着压力的升高，两条线有明显逼近的趋势。后续可根据实际的应用情况对计算公式进行修正处理，进一步提高精度。在9 216组工况中有4 586组误差值低于5%，精度甚至优于密度的计算值。总平均相对误差值为7.13%。

图5中，选取100～1 000 MPa范围内的6组压力值，绘制焓值相对误差与温度的关系图。6组压力的焓值平均误差分别为10.68%、7.33%、5.50%、4.33%、3.88%、3.51%，在低温附近误差较大。当温度达到400 K时，误差降到20%。在温度超过1 000 K后，相对误差值降到10%以内。由于超高压工况往往伴随着高温，所以此次研究的关注点主要集中于高温高压领域。

3.3 熵

计算空气熵的方程由空气亥姆霍兹能状态方程推导得到，一般式如式（19）所示

s/R=τ[（（∂α^0）/∂δ）_δ+（（∂α^r）/∂τ）_δ ]-α^0-α^r （19）

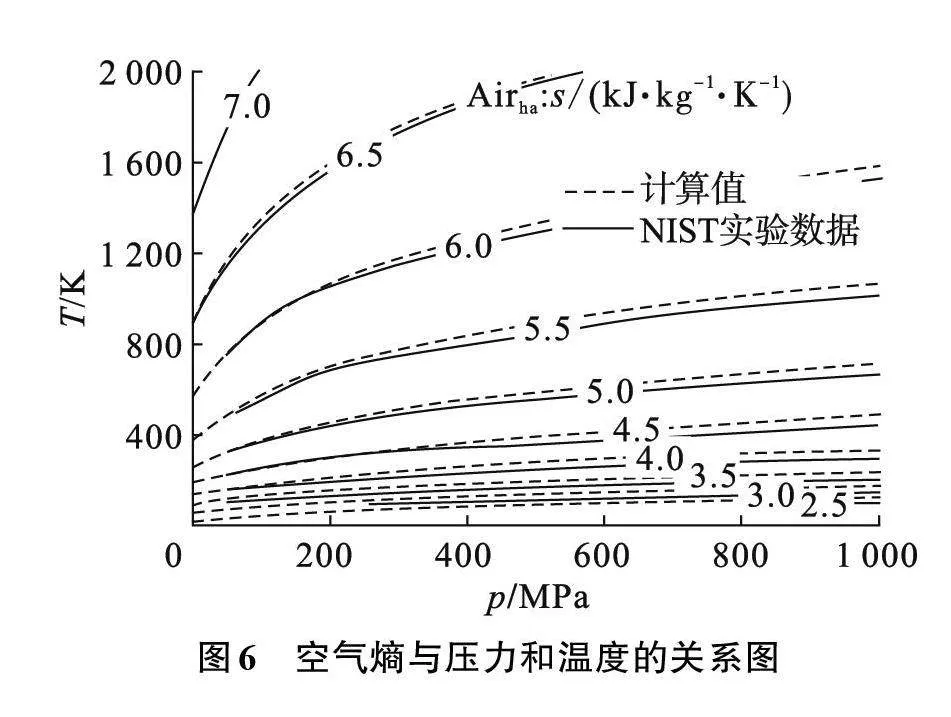
如图6所示，以等熵值线表示温度T为50～2 000 K、压力p为100～1 000 MPa时空气熵值与压力和温度的分布情况。空气亥姆霍兹能状态方程计算的结果和NIST数据库的结果具有较好的重合性，在熵值取6.5及以上时，两线几乎完全重合。在压力低于400 MPa的范围内，两线的重合情况也较为理想。随着压力的升高，误差值有逐渐变大的趋势。在9 216组工况中有8 711组误差值低于5%，总平均相对误差为1.39%。

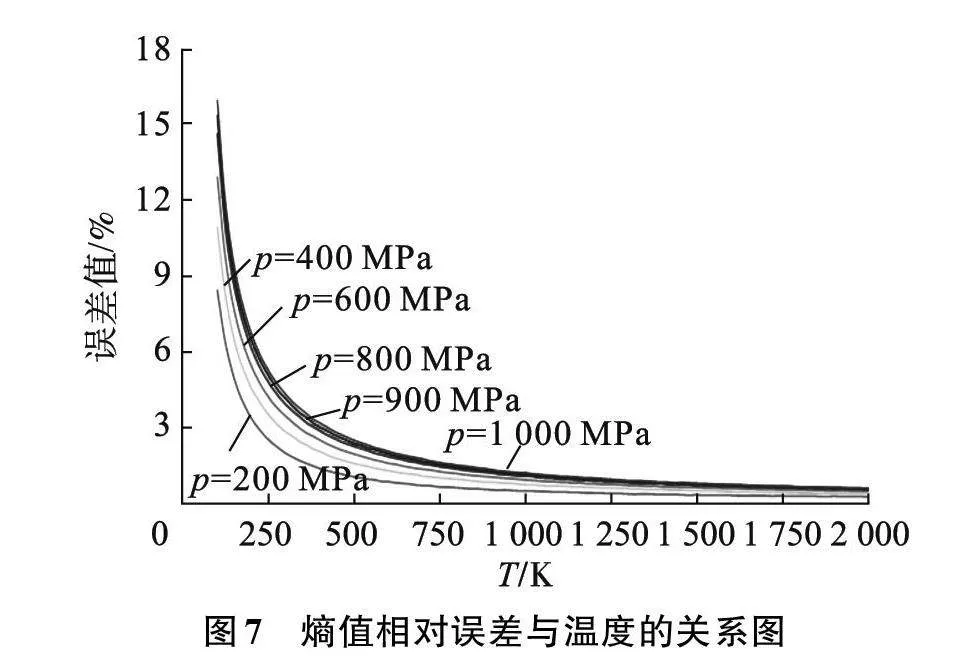
图7中，选取100～1 000 MPa范围内的6组压力值，绘制熵值相对误差与温度的关系图。6组压力的熵值的平均误差分别为 0.87%、1.28%、1.58%、1.81%、1.92%、2.01%。从图7中可以看出，温度较低时相对误差值较大，但最大值仅为15.87%；随着温度升高到200 K，误差值已全部下降到8%以内；且在达到600 K以后，误差均低于2%；熵值的平均相对误差值为1.39%，其计算精度仅次于动力黏度。

3.4 动力黏度

如图8所示，以等动力黏度曲线表示温度T为50～2 000 K、压力p为100～1 000 MPa时，空气焓值与压力和温度的分布情况。动力黏度计算值与对比值曲线并不完全重合，仅在温度和压力较低的区域范围吻合。但实际的相对误差几乎都低于1%。造成这种情况的主要原因在于动力黏度的数值较小，因此在数值计算时，进行106倍放大，使得差值也被同步放大。从曲线的变化趋势可以看出，计算值曲线和对比值曲线的变化情况基本一致。在9 216组工况中有8 841组误差值低于5%，总平均相对误差为0.64%。

图9中，选取100～1 000 MPa范围内的6组压力值，绘制动力黏度相对误差与温度的关系图。6组压力的动力黏度平均误差分别为0.74%、0.69%、0.62%、0.57%、0.54%、0.52%。从曲线的变化规律可以看到，仅在低温区域，相对误差值超过10%。当温度达到200 K时，所有误差值均低于5%，且后续所有的误差值基本控制在0%左右，具有热力学参数计算中最高的精度。整组数据的平均相对误差为0.64%，为5个参数中的最低值。

3.5 导热系数

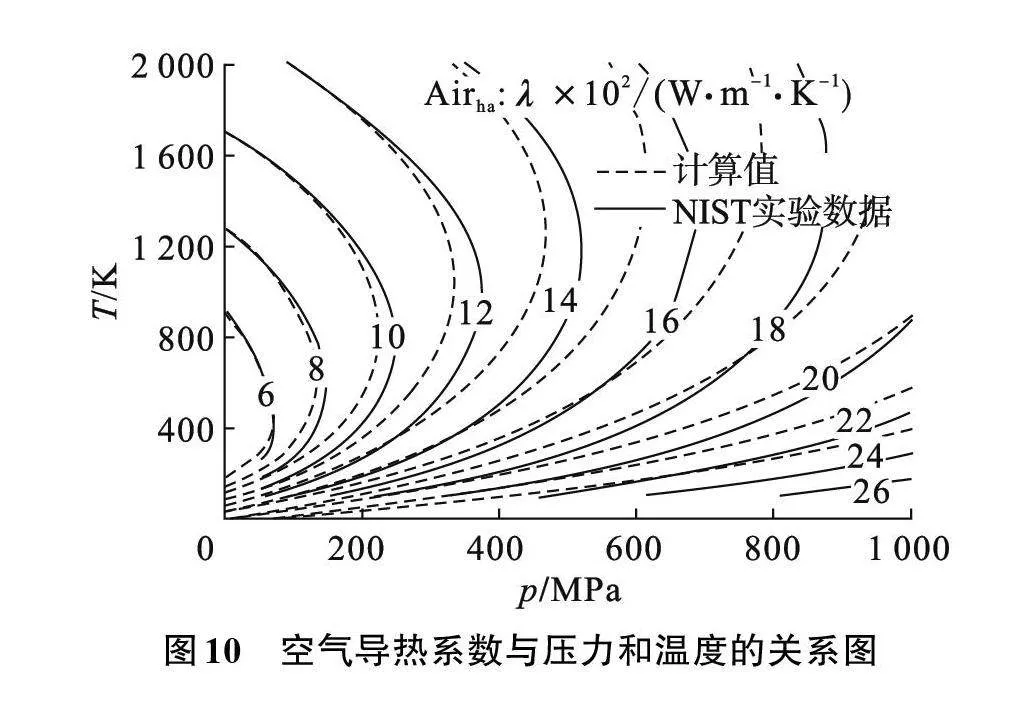
如图10所示，以等导热系数曲线表示温度T为50～2 000 K、压力p为100～1 000 MPa时，空气导热系数与压力和温度的分布情况。压力低于200 MPa时，两条曲线的重合情况较为理想；随着压力的升高，偏移量逐渐增加，且情况同动力黏度类似。对计算结果进行100倍放大，导致误差也被放大。在9 216组工况中有3 783组误差值低于5%，总平均相对误差为6.91%。

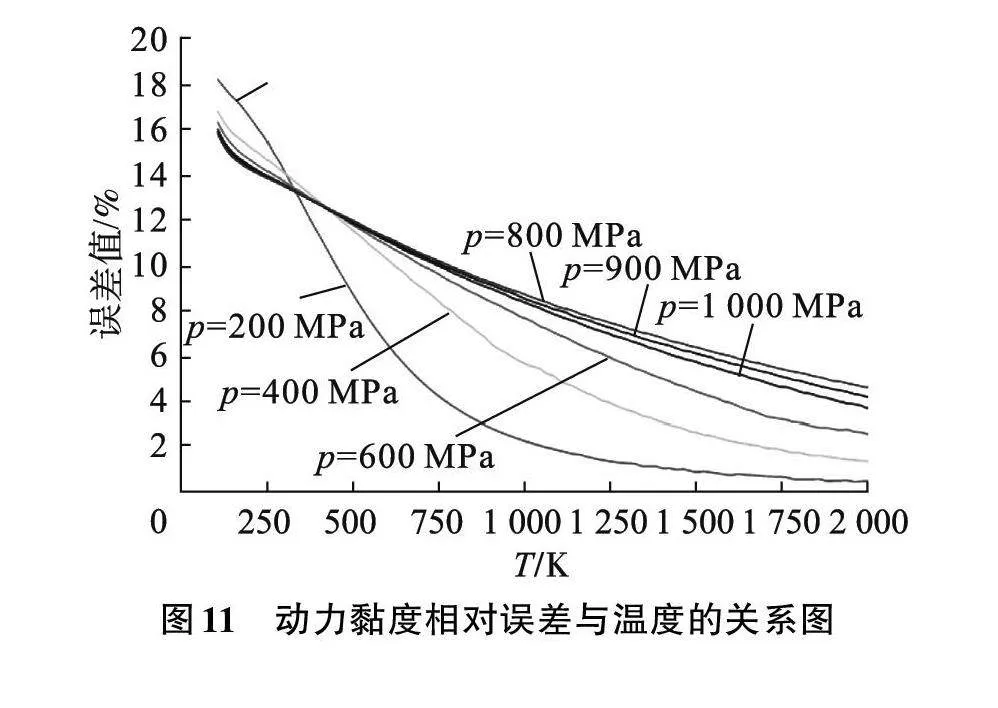
图11中，选取100～1 000 MPa范围内的6组压力值，绘制动力黏度相对误差与温度的关系图。6组压力的动力黏度平均误差分别为4.72%、6.75%、7.90%、8.59%、8.81%、8.98%。从这6组数据可以验证之前得到的结论，即随着压力的升高，误差值在增加。但从图11中可以看出，当温度超过800K后，相对误差值均低于10%，符合高温高压范围的研究目标。

4 结论

本文运用空气亥姆霍兹能状态方程和输运物性方程组，对50～1 000 MPa压力范围和100～2 000 K温度范围内的9 216组参数进行计算。在EXCEL中调用CoolProp软件获得NIST实验测得的超高压空气物性数据，对计算结果进行计算比较，求得各组工况的误差。

从计算结果可以看出，计算曲线与数据库标准曲线吻合度较为理想，且变化趋势类似。5个热力学参数的相对误差较小，平均相对误差分别为5.73%、7.13%、1.39%、0.64%、6.91%。相对误差值均随温度升高而降低，尤其是在高温超高压的条件下，计算的结果与标准数据几乎对应，满足超高压工况的研究要求。故可以采用空气亥姆霍兹状态方程与空气输运物性参数方程作为超高压气体研究的计算模型。

参考文献（References）：

［1］ 唐志共，许晓斌，杨彦广，等.高超声速风洞气动力试验技术进展［J］.航空学报，2015，36（1）：86-97.

［2］ 齐超，刘拓，易满满.基于亥姆霍兹自由能的实际气体状态方程［J］.化工装备技术， 2022， 43（4）： 21-25.

［3］ Jacobsen R T，Stewart R B，Jahangiri M.Thermodynamic properties of nitrogen from the freezing line to 2 000 K at pressures to 1 000 MPa［J］. Journal of Physical amp; Chemical Reference Data，1986，15（2）：735-909.

［4］ Younglove B A.Thermophysical properties of fluids.i. argon，ethylene，parahydrogen，nitrogen，nitrogen trifluoride，and oxygen［J］.Journal of Physical amp; Chemical Reference Data，1982，11（1）：1-11.

［5］ Sifner O，Klomfar J.Thermodynamic properties of xenon from the triple point to 800 K with pressures up to 350 MPa［J］.Journal of Physical amp; Chemical Reference Data， 1994，23（1）：63-152.

［6］ Cottrell T，Paterson S.An equation of state applicable to gases at densities near that of the solid and temperature far above the critical［J］.Proceedings of the Royal Society A，1952，213（1）：214.

［7］ 董赛鹰，芶清泉，李萍，等.高温高压气体的状态方程与热力学性质［J］.原子与分子物理学报，2005（1）：101-104.

［8］ 芶清泉，董赛鹰，李萍，等.高密度氩气的原子间相互作用与状态方程［J］.原子与分子物理学报，2004（3）：466-470.

［9］ 张平，李洪烈，李灿，等.基于亥姆霍兹能量方程的天然气密度计算方法［J］.化工自动化及仪表，2021，48（1）：49-52.

［10］ Lemmon E W，Jacobsen R T，Penoncello S G，et al.Thermodynamic properties of air and mixtures of nitrogen， argon， and oxygen from 60 to 2 000 K at pressures to 2 000 MPa［J］.Journal of Physical amp; Chemical Reference Data，2000， 29（3）：331-385.

［11］ 孟令军，陈国邦，黄忠杰，等.空气亥姆霍兹能方程p-ρ-T性质考察［J］.低温工程，2008（1）：7-13.

［12］ Stiel-Thodos I F.Viscosities of gases and gas mixture［M］.Moscow：Fizmat Press，1959.

［13］ Lemmon E W，Jacobsen R T.Viscosity and thermal conductivity equations for nitrogen，oxygen，argon，and air［J］.International Journal of Thermophysics，2004，25（1）：21-69.

［14］ Olchowy G A，Sengers J V.A simplified representation for the thermal conductivity of fluids in the critical region［J］.International Journal of Thermophysics，1989，10（2）：10.

［15］ Bell I H，Wronski J，Quoilin S.Pure and pseudo-pure fluid thermophysical property evaluation and the open-source thermophysical property library coolProp［J］.American Chemical Society，2014，53（6）：2498-2508.

（责任编辑：吴萍" 英文审校：张微）