如何命制一份高中数学期末考试试卷

摘  要：高中数学期末考试属于学业水平考试，要按照学业质量标准和内容要求命制试卷. 在命制试卷时，要设计合理的试卷结构，制定命题双向多维细目表，根据考查目标命制试题，制定合适的评分标准. 在命制试题时，要坚持导向性、科学性、整体性、适度性和创新性的命题原则，具体可以采用知识点整合、教材例题和习题变式、试题类比、构造逆命题、经典试题特殊化和一般化等命题方法.

关键词：高中数学；期末考试；试卷设计；命题原则；命题方法

高中数学期末考试旨在评价学生经过一个学期的数学学习后在核心知识、思想方法和关键能力三个维度的学业质量水平. 高中数学期末考试属于学业水平测试，《普通高中数学课程标准（2017年版2020年修订）》指出：数学学业质量水平是高中毕业的数学学业水平考试的命题依据. 因此，笔者围绕高中数学期末考试的试卷设计、命题原则和命题方法，谈一些思考与实践.

一、高中数学期末考试的试卷设计

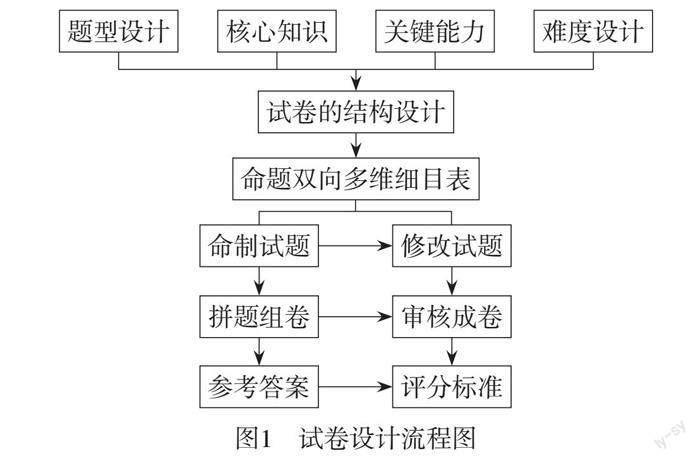
高中数学期末考试试卷，要遵照学业质量水平一的要求，围绕核心知识、关键能力进行试卷结构设计，经历制定命题双向多维细目表，命题组卷、修改试题、审核成卷等过程，其设计流程如图1所示.

[题型设计][核心知识][关键能力][难度设计][试卷的结构设计] [命题双向多维细目表] [命制试题][修改试题][拼题组卷][审核成卷] [参考答案][评分标准] [图1试卷设计流程图]

1. 高中数学期末考试的试卷结构

试卷结构包括知识结构、题型结构、能力结构和难度结构四个方面. 基于高中数学课程内容和新高考数学试卷结构，确定高中数学期末考试的试卷结构如下.

知识结构：由学期教学内容确定，涉及函数、几何与代数、概率与统计、数学建模活动与数学探究活动等主题.

题型结构：包含单选题（第1 ～ 8题，共计40分）、多选题（第9 ～ 12题，共计20分）、填空题（第13 ～ 16题，共计20分）、解答题（第17 ～ 22题，共计70分）四种题型，卷面总分为150分.

能力结构：结合具体试题考查学生的抽象概括、推理论证、运算求解、直观想象、数据分析和数学建模能力.

难度结构：试题难度分为容易题、中等题和难题3个层次. 高中数学期末考试试卷的难度宜控制在0.65左右，容易题占60%，中等题占30%，难题占10%. 容易题标准为[p>0.70]（[p]为难度），中等题标准为[0.35≤][p≤ 0.70]，难题标准为[p<0.35].

2. 高中数学期末考试的命题双向多维细目表

高中数学期末考试试题的命制可以从问题情境、核心知识、核心知识评价要求、思想方法和关键能力等維度设计双向多维细目表，如表1所示.

说明：（1）问题情境分为现实情境、数学情境和科学情境，问题分为简单问题（A）、较复杂问题（B）和复杂问题（C）三个层次. 例如，“数学A”指数学情境中的简单问题.

（2）核心知识的评价分为了解、理解、掌握和运用四个认知层次，且高一级的层次要求包含低一级的层次要求.

（3）思想方法主要包括转化与化归、函数与方程、数形结合、分类与整合、特殊与一般、概率与统计等.

（4）关键能力主要指抽象概括、推理论证、运算求解、直观想象、数据分析、数学建模等.

3. 高中数学期末考试的评分标准

（1）制定评分说明.

在高中数学期末考试中，选择题电脑阅卷，评分客观；填空题答案明确、具体，评分公正. 而解答题的评分与评卷人有关，因此要基于以下要点制定解答题的评分说明.

① 参考答案和评分标准给出了一种或几种解法供参考，如果学生的解法和参考答案不同，可以根据试题主要考查的知识点和能力水平对照评分标准给予相应的分数.

② 对于解答题中的计算题，当学生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的得分，但所给分数不得超过该部分正确解答应得分数的一半；如果后续部分的解答出现较严重的错误，就不再给分.

③ 解答右端所注分数，表示学生正确做到这一步应得的累加分数.

（2）制定评分标准.

高中数学期末考试题的评分标准要依据考查目标和认知水平确定. 具体可以根据SOLO分类评价中的“单一结构水平、多元结构水平、关联水平、扩展抽象水平”制定数学解答题的评分标准（详见例11）.

二、高中数学期末考试的命题原则

1. 导向性原则

高中数学期末考试题应该依据学业质量标准和课程内容进行命制，注重对学生数学核心素养的考查，处理好数学核心素养与知识技能之间的关系，要充分考虑试题对教学的导向作用.

例1  已知函数[fx=3sinxcosx-cos2x].

（1）求函数[fx]的最小正周期；

（2）当[x∈-π6， π2]时，讨论[fx]的单调性并求其值域.

【评析】此题为海南省2021—2022学年第一学期期末学业水平考试高一数学第20题，源于人教A版《普通高中教科书·数学》（以下统称“人教A版教材”）必修第一册第206页例5和第227页例9. 以三角函数知识的运用为问题情境，以三角函数性质的探讨为设问角度，考查三角函数和三角变换的核心知识，考查函数与方程和转化与化归等思想，以及运算求解和直观想象等能力. 此题仅改变了人教A版教材例题中的函数表达式，围绕主干知识进行命制，设问方式常规，注重对通性通法的考查，突出试题的基础性和综合性，符合数学学业质量水平一的要求，具有较好的教学导向.

2. 科学性原则

高中数学期末考试题的命制应该强调科学性，避免试题中出现政治性、科学性错误，同时要注意表述简洁、明确，规范使用数学语言，不引起歧义. 试题所给条件要足以推出结论，且不出现冗余条件.

例2  已知函数[fx]的定义域为[R]，且[fx+1+][fx-1=2，] [fx+2]为偶函数，若[f0=2，] 则[k=1115fk]等于（    ）.

（A） 116 （B） 115

（C） 114 （D） 113

【评析】此题为广东省广州市2023届高三调研测试（数学）第7题，以抽象函数为问题情境，以求和为设问角度，考查函数的周期性，考查转化与化归和数形结合思想，以及逻辑推理、直观想象和数学抽象素养. 此题表述规范，关键在于基于[fx+1+fx-1=2]发现函数[fx]的周期性，即[fx]是周期函数，且周期为4. 从解题过程来看，由[f0=2]及函数的周期性就可得答案C，因此此题中的条件“[fx+2]为偶函数”冗余，应该删掉.

3. 整体性原则

高中数学期末考试题的命制要整体把握试题的评价功能，关注核心知识、思想方法和关键能力的评价要求，突出问题本质，注重知识联系，合理设计问题，以提高试题的区分度.

例3  已知函数[fx=cos2x+acosx，] 当[a=2]时，[fx]的最小值为      ；若函数[fx]的最大值为[2]，则[a]的值为       .（第一空2分，第二空3分.）

【评析】此题为福建省漳州市2021—2022学年第一学期期末考试高一数学第16题，以三角函数为问题情境，以函数的最值为设问角度，将余弦函数、三角变换、二次函数等核心知识进行整合，考查函数与方程、化归与转化和分类讨论思想，以及运算求解和直观想象等能力. 此题遵循整体性的命题原则，第一空基于基础性要求设问，第二空基于综合性要求进行逆向设问，这种并列式的设问方式有利于提高试题的区分度，有效评价学生的学业质量水平.

4. 适度性原则

高中数学期末考试题要能有效评价学生的学业质量水平. 因此，高中数学期末考试题的命制要注重难度适中，以保证学业水平考试的信度和效度，使试题具有良好的区分度和一定的覆盖面.

例4  如图2，在平面直角坐标系中，角[α，β]的始边均为[x]轴正半轴，终边分别与圆[O]交于[A，B]两点，若[α∈7π12，π，β=π12]，且点[A]的坐标为[A-2，m].

（1）若[tan2α=-43]，求实数[m]的值；

（2）若[tan∠AOB=-34]，求[cos2α]的值.

【评析】此题为湖北省黄冈市2020—2021学年第一学期期末考试高一数学第19题，以角的终边与圆相交为问题情境，以求值为设问角度，考查三角函数的定义和三角变换等核心知识，考查函数与方程和转化与化归思想，以及运算求解能力. 此题难度适中，注重基础性和综合性，符合数学学业质量水平一的要求.

5. 创新性原则

高中数学期末考试要编制适量的创新性试题. 创新性主要体现在问题情境、设问角度和解法建构上，能有效评价学生的知识迁移能力和创新意识.

例5  已知函数[fx=xex]，其中[e]是自然对数的底数.

（1）求函数[fx]的最小值；

（2）设函数[gx=fx-xlnx-kx]，当[k≤ 2]时，证明：[gx>0].

【评析】此题为广东省广州市“六区”2021—2022学年第二学期期末考试高二数学第22题，源于人教A版教材选择性必修第二册第104页第18题. 此题改变了原题中的函数结构，以导数应用为问题情境，以求函数的最小值和证明不等式为设问角度，考查导数的核心知识，考查函数与方程和转化与化归思想，以及推理论证、数学建模、运算求解、直观想象等能力，能有效评价学生的创新意识，体现了创新性的命题原则.

三、高中数学期末考试的命题方法

高中数学期末考试题的命制应该考虑问题情境、设问角度和考查目标三个要素，常用的命题方法有如下六种.

1. 整合多个核心知识点

例6 （多选题）已知[x，y∈R]，且[0

（A）[sinx

（C）[2x-y<1] （D）[xx+1

【评析】此题为江苏省南京市2021—2022学年第一学期期末考试高一数学第9题，其采用知识点整合的命题方法，以比较大小为问题情境，以不等关系为设问角度，综合考查正弦函数、幂函数、指数函数等核心知识，以及函数思想和推理论证能力，体现了基础性的考查要求.

2. 改变教材例题和习题的条件或结论

例7  如圖3，在四棱锥[B-ACDE]中，[DE]∥[AC]，[AC][⊥]平面[BCD]，[AC=2DE=4]，[BC=2]，[DC=1]，[∠BCD=60°]，[F]为[AC]的中点.

（1）证明：[DF]∥平面[ABE]；

（2）过点[D]作平行于平面[ABE]的截面，画出该截面，说明理由，并求夹在该截面与平面[ABE]之间的几何体的体积.

【评析】此题为广东省广州市“六区”2021—2022学年第二学期期末考试高一数学第21题，是人教A版教材必修第二册第138页例3的变式题. 此题将原题中的六面体改为四棱锥，同时增设了位置关系和度量关系条件，改变了设问角度，以基本空间图形为问题情境，以位置关系的证明和几何体体积计算为设问角度，考查直线与平面平行（垂直）、棱锥体积公式等核心知识，考查转化与化归思想，以及推理论证、运算求解和直观想象等能力，体现了综合性的考查要求.

3. 类比高考题或模拟题

例8  已知双曲线[C]：[x2a2-y2b2=1 a>0，b>0]的右焦点为[Fc，0]，离心率为[2]，直线[x=a2c]与[C]的一条渐近线交于点[P]，且[PF=3].

（1）求双曲线[C]的标准方程；

（2）设[Q]为双曲线[C]右支上的一个动点，在[x]轴的负半轴上是否存在定点[M]，使得[∠QFM=2∠QMF？]若存在，求出点[M]的坐标；若不存在，试说明理由.

【评析】此题为江苏省徐州市2021—2022学年第一学期高二数学第22题，类比2021年1月“八省市”高考数学模拟演练第21题的结构命制，改变了部分条件和设问方式. 以双曲线为问题情境，以求双曲线标准方程和对双曲线几何性质的探究为设问角度，考查双曲线的核心知识，考查方程思想、数形结合思想和分类讨论思想，以及推理论证、运算求解和直观想象等能力，体现综合性和创新性的考查要求.

4. 交换命题的条件和结论

例9  已知椭圆[C]：[x2a2+y2b2=1] [a>b>0]的离心率为[32]，F1，F2分别为椭圆C的左、右焦点，M为椭圆C上一点，[△MF1F2]的周长为[4+23].

（1）求椭圆C的方程；

（2）P为圆[x2+y2=5]上任意一點，过点P作椭圆C的两条切线，切点分别为[A，B]，判断[PA · PB]是否为定值？若是，求出定值；若不是，说明理由.

【评析】此题为2021年广东省广州市普通高中毕业班调研测试数学试卷第21题. 以椭圆为问题情境，以求轨迹方程和定值为设问角度，考查椭圆的定义与性质、直线与椭圆的位置关系等核心知识，考查转化与化归和数形结合思想，以及运算求解能力. 此题第（2）小题源于经典的轨迹问题：椭圆[b2x2+a2y2=a2b2] [a>b>0]两条互相垂直切线的交点的轨迹方程是[x2+y2=a2+b2]（椭圆的蒙日圆），从构造逆命题的视角设计问题.

5. 经典试题特殊化

例10  在等差数列[an]中，已知[a3+a4=12]，则数列[an]的前[6]项之和为（    ）.

（A）[12] （B）[32]

（C）[36] （D）[72]

【评析】此题为广东省广州市“六区”2021—2022学年第一学期期末考试高二数学第3题，将经典试题“在等差数列[an]中，若[p，q，s，t∈N?]，且[p+q=][s+t]，则[ap+aq=as+at]”特殊化，以等数差列为问题情境，以数列求和为设问角度，考查等差数列的核心知识，考查转化与化归思想，以及运算求解能力，体现基础性的考查要求.

6. 经典试题一般化

例11  已知直线[l]与椭圆[C]：[x2a2+y2b2=1 a>b>0]交于[A，B]两点，且经过椭圆[C]的右焦点[F].

（1）若[l]与[x]轴垂直，且点[A]的坐标为[1， 22]，求[C]的方程；

（2）若[O]为坐标原点，在[x]轴上是否存在异于点[F]的点[M]，使得[∠OMA=∠OMB]？若存在，求点[M]的坐标；若不存在，说明理由.

解：（1）当直线[l]与[x]轴垂直时，依题意知椭圆[C]的右焦点为[F1，0]，

所以[a2-b2=1]. …1分

将点[A]的坐标代入，得[1a2+12b2=1]. …2分

所以[a2=2，b2=1].…3分

所以椭圆[C]的方程为[x22+y2=1].…4分

（2）设椭圆[C]的右焦点坐标为[Fc，0].

假设存在点[Mm，0][m≠ c]，使得[∠OMA=∠OMB]成立.

当直线[l]与[x]轴垂直时，存在无数个点[Mm，0][m≠c]，使得[∠OMA=∠OMB].…5分

当直线[l]与[x]轴不垂直时，设直线[l]的方程为[y=kx-c].

若[k=0]，则[A，B]为椭圆左、右顶点，故存在点[Mm，0][m>a]，使得[∠OMA=∠OMB].…6分

若[k ≠ 0]，将[y = kx - c]代入[x2a2 + y2b2 = 1]，得[a2k2+b2x2-2ca2k2x+a2c2k2-b2=0].…7分

设[Ax1，y1，Bx2，y2]，

则[x1+x2=2ca2k2a2k2+b2]，[x1x2=a2c2k2-b2a2k2+b2]. …8分

因为[∠OMA=∠OMB]，

所以直线[AM，BM]的斜率之和为0，

即[kAM+kBM=y1x1-m+y2x2-m=y1x2-m+y2x1-mx1-mx2-m=0.]

… 9分

所以[y1x2-m+y2x1-m=0]，

即[kx1-cx2-m+kx2-cx1-m=0].

因为[k≠ 0]，

所以[2x1x2-m+cx1+x2+2mc=0]，

即[2a2c2k2-b2a2k2+b2-2ca2k2m+ca2k2+b2+2mca2k2+b2a2k2+b2=0].

…10分

所以[2a2c2k2-b2-2ca2k2m+c+2mca2k2+b2=0.]

解得[m=a2c].…11分

故存在点[Ma2c，0]，使得[∠OMA=∠OMB].

…12分

【评析】此题为广州市黄埔区2022—2023学年第一学期期末高三数学第22题，是对2018年高考数学全国Ⅰ卷理科第19题的一般化. 以椭圆为问题情境，以求椭圆方程与判定对称轴是否平分“焦点弦张角”为设问角度，考查椭圆的标准方程、直线与椭圆的位置关系等核心知识，考查转化与化归和数形结合思想，以及抽象概括、推理论证和运算求解等能力，体现综合性和创新性的考查要求.

四、结束语

高中数学期末试卷的命制是高中数学教师应该具备的基本素养. 试题命制方法多样，一般要经历选题、改题和编题的过程，是一项十分艰辛的工作. 如何依据数学学业水平考试要求命制一份高质量的高中数学期末试卷，是值得深入探讨的问题.

参考文献：

［1］中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）［M］. 北京：人民教育出版社，2020.

［2］任子朝. 中学生数学学业测试研究［M］. 北京：教育科学出版社，2001.

［3］教育部考试中心. 高考数学测量理论与实践［M］. 北京：高等教育出版社，2004.

［4］曾辛金，肖凌戆. 基于SOLO评价理论的数学解答题评分标准研究：以一道函数与导数解答题为例［J］. 中国数学教育（高中版），2019（7 / 8）：10-13.