考虑驾驶员心生理参数的桥隧过渡段安全间距研究

乔建刚,王 傑,谢一丹,陈彦欣

(1.河北工业大学 土木与交通学院, 天津 300401;2.河北省高速公路延崇筹建处, 河北 张家口 075000)

目前我国高速公路的建设已由平原转向山区,山区高速公路由于地形复杂、桥隧比例大,加之桥隧路段易诱使交通事故的发生[1],导致高速公路运营存在较大风险。目前国内外学者对桥隧路段进行了研究,主要有:Ma等[2]分析了不同断面位置、交通流量与交通事故发生率的相关性。倪娜等[3]从光环境、速度等角度探讨了桥隧密集路段的交通流特性。王建民[4]提出了桥梁安全状态的划分标准以及评价方法。乔建刚等[5]基于可拓学理论对多个评价指标进行了量化分析,建立了桥梁安全评价模型。Han等[6]对超重型卡车在桥梁行车的负荷进行了研究及安全评估。潘国兵等[7]依据“调节滞后”等理论,分析了隧道亮度变化率与瞳孔直径的关系。Li等[8]分析了交通流特性与隧道亮度的关系,对隧道照明进行了动态控制。康良国等[9]研究了员工心理安全感的安全信息认知的偏好特征。Foy等[10]从驾驶员的生理反应角度分析了道路环境变化对心理负荷的影响。Kircher等[11]和Han等[12]分析了驾驶员在隧道段上视觉特性变化与道路线形、光环境的变化规律。Miller等[13]采用驾驶员心率、心博间期标准差基础指标、车速和制动探讨了隧道行车驾驶员压力与驾驶绩效的关系。吴艳霞等[14]研究了车辆速度一致性、驾驶员心生理反应与穿城镇道路行车安全的影响规律。李立治等[15]针对驾驶风格进行了分类和识别。综上,国内外学者主要围绕桥梁、隧道安全评估、驾驶员视觉特性、心生理反应[16]进行了对单一路段的行车安全分析,从驾驶行为角度对桥隧过渡段的研究较少,开展基于驾驶行为的桥隧过渡段的安全间距研究具有重要意义。

1 基于小波变换的心电信号降噪

驾驶员交通行为随着道路线形与环境的变化而变化,驾驶员的心率会产生随机变化,其心率随着环境的变化产生随机信号。小波变换(wavelet transform,WT)可在时域和频域中同时进行多种分辨率的信号分析,并适用于处理瞬态信号,广泛用于多种学科研究中,小波变换降噪基本原理可用图1表示。

图1 小波变换降噪原理示意图

小波函数ψ(t)须满足:

(1)

(2)

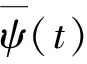
(3)

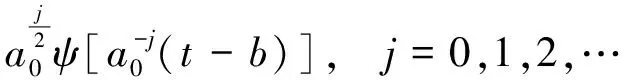
(4)

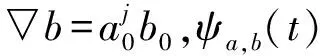
(5)

令a0=2,b0=1,

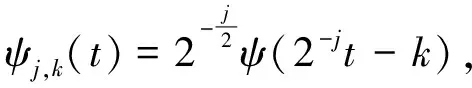
j=0,1,2,…;k∈Z

(6)

x(t)的离散小波变换为:

(7)

选择软阈值法对该心率进行去噪处理,选择db4小波进行分解,得到降噪信号如图2所示。

图2 心率增长率降噪信号曲线

对比图2可以看出,通过小波阈值进行滤波处理以后,大大降低了原始信号的噪声,使降噪后信号的波峰明显,心率信号的周期性表现明显。

2 试验方案及数据采集

2.1 试验时间、地点

选取延崇高速、太行山高速公路等作为数据采集的试验段,实验时间选择正常工作日9∶00—17∶00,车辆处于自由流行驶状态,实验天气选择晴天。

2.2 试验仪器

该高速公路交通流中主要以小型车为主,因此实验车辆选择为车况正常的小型车;心生理信号采集仪采用康飞KF2型仪器采集驾驶员的心率等数据;V-Box数据采集器和非接触式五轮仪采集道路线形参数、速度数据;隧道内外的光照强度用GM1020照度计采集。

2.3 试验对象

根据统计学最小样本量的计算选择20名驾驶员,年龄区间为[23,40](均值为28.1,标准差σ为4.3);驾龄区间为[3,10](均值为5.9,标准差σ为2.8) 并且熟悉试验道路,试验前对平静状态下的心率进行检测。

整理试验过程中距离、车速及对应的驾驶员心率增长率,部分数据见表1。

表1 桥隧段速度、心率增长率和照度统计(部分)

3 桥隧路段行车安全性分析

目前道路行车安全评价常见的指标有速度差和驾驶员心率增长率,当不同路段速度差大于20 km/h以上时,路段安全性低[17];心率增长率大于紧张阈值27%,驾驶员将因紧张导致驾驶操作失误增多[18-19]。因此,通过桥隧路段的环境照度变化和车辆速度变化与驾驶员心生理变化的关系对路段的行车安全性进行分析。

3.1 隧道口心率与照度的关系

由于照度是一个绝对值,并不能反映人的明暗适应规律,因此为更好地分析驾驶员对环境照度的适应情况,采用照度变化率作为评价指标:

(8)

其中:Er为照度变化率(%);Et、Et-1分别为t点与t-1点的照度值(lux)。

通过计算得到的照度变化率分析其与距离和心率增长率的关系,如图3所示。

照度变化率在隧道洞前50～200 m区域内基本不变,在洞外20 m至洞内20 m区域逐渐增大。当照度变化率增大至54%时,心率增长率为27%,此时心率增长率与照度变化率的关系模型为:

(9)

其中:y1为心率增长率(%);Er为照度变化率(%)。式(9)的相关系数R=0.882 02,通过F检验。

图3 照度变化率、心率增长率变化情况

3.2 桥隧路段速度特性分析

驾驶员在桥隧路段行车时,由于道路线形的变化、伸缩缝、道路路面结构的变化容易引起速度的改变,进而导致驾驶员的心率发生变化。桥隧相邻路段断面布置见图4。

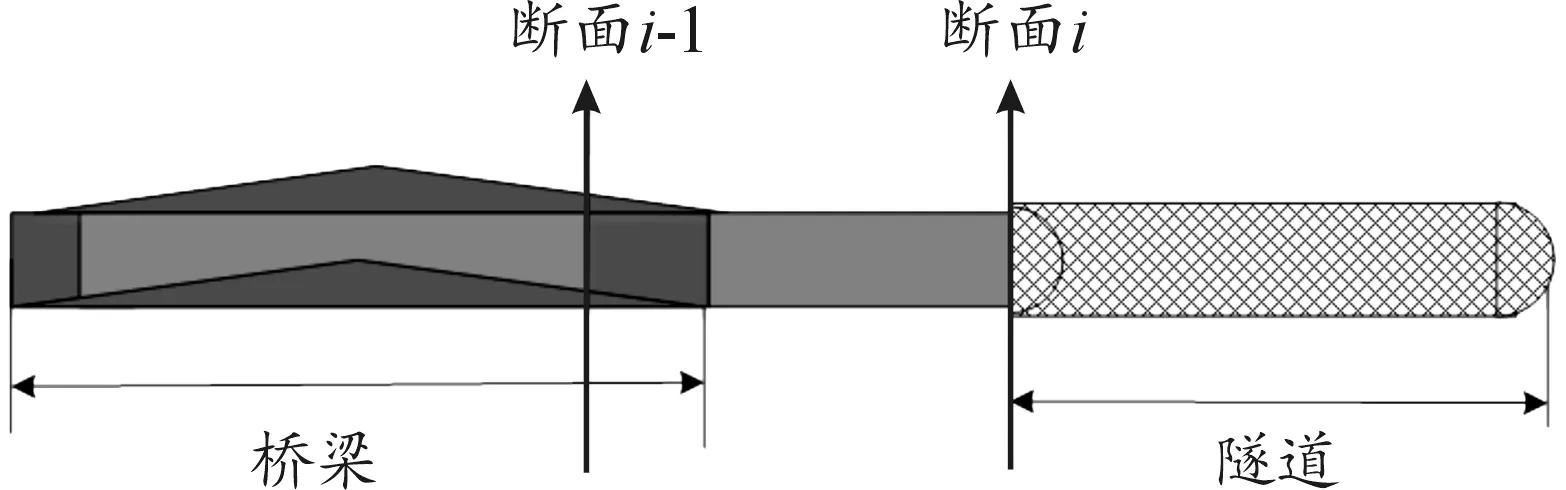
图4 相邻路段断面示意图

3.2.1桥隧路段速度一致性分析

以相邻路段的车辆运行速度差作为评价指标[17],对道路协调性进行评价,差值越小,协调性越好,速度差的计算公式如下:

Δv85=v85i-v85(i-1)

(10)

其中:|Δv85|表示相邻路段的85%位车速差;v85i和v85(i-1)分别为断面i与断面i的前一断面的85%位车速。

通过采集的速度数据分析驾驶员桥隧路段的驾驶行为的变化,如图5、6所示。

图5 速度与距离的关系图(桥梁路段)

在桥梁路段行车速度整体呈现W型变化趋势,在桥梁出入口过渡段速度呈现V型变化。在桥梁前100～200 m范围内行驶时,驾驶员的速度在90～95 km/h范围内波动,速度差值小于5 km/h;驶入桥梁的过程中,在距离桥梁前20～100 m范围内,速度逐渐降低,速度差在5～15 km/h之间,随着进入桥梁,速度逐渐增加,然后趋于稳定。同样,驶出桥梁的过程中,速度呈现先减小后增大的变化趋势,在桥梁出口前58 m开始减速,在出口后12 m降为最小,在减速过程中由87.3 km/h降为76.5 km/h;出桥梁后77 m,速度趋于稳定。

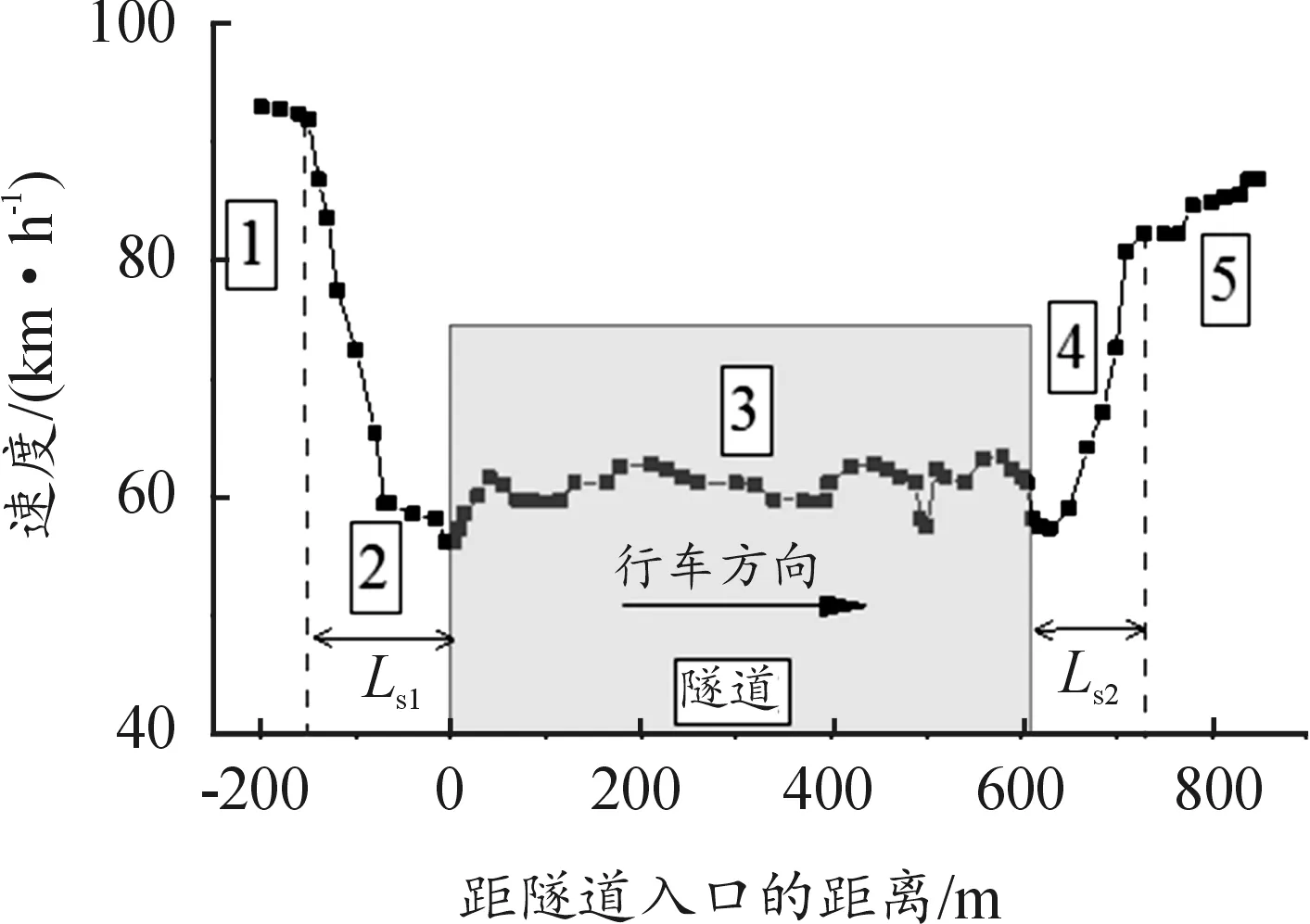
图6 速度与距离的关系图(隧道路段)

在隧道路段速度整体呈现U型变化趋势,在隧道出入口过渡段速度呈现L型变化趋势。在隧道前150～200 m范围内行驶时,驾驶员的速度基本维持在92 km/h,在隧道前150 m,驾驶员的行车速度急剧下降,降幅超过20 km/h;在隧道内 2 m速度降为最低,为56.2 km/h。随着进入隧道,行车速度有小幅度的增加,增至62.4 km/h;驶出隧道的过程中,在距离隧道出口前52 m,速度逐渐降低至57.4 km/h,驶出隧道后98 m,速度趋于稳定,由59.6 km/h恢复至86.8 km/h,速度差值大于20 km/h。

由图5和图6实车试验的数据,计算桥梁段、隧道段的车速如表2所示。在桥梁段上的平均车速为82.6 km/h,在隧道段上的平均车速为60.8 km/h,从桥梁驶入隧道车辆速度逐渐减小。在桥梁段速度差最大为7.8 km/h,在隧道路段速度差最大为26.3 km/h,速度差越大则车辆纵向冲突增多,容易导致交通事故[20]。从速度来看,这些路段明显存在安全隐患。

表2 速度特性对比 (km·h-1)

3.2.2桥隧路段心生理特性分析

速度的变化以及环境照度的变化都会导致驾驶员的心生理产生变化。驾驶员在桥隧路段的心率增长率与距离的变化规律,如图7和图8所示。

图7 心率增长率与距离的关系图(桥梁路段)

在桥梁前60～200 m范围内,驾驶员心率增长率都保持在27%以下,说明驾驶员处于舒适状态,在桥梁前90 m,驾驶员心率增长率开始逐渐增大,在进入桥梁后0～10 m,驾驶员心率增长率增大至30.8%;在驶出桥梁前40 m,驾驶员心率增长率逐渐增大,在出口达到最大值为30.4%,超过舒适阈值,在距离出口72 m后,心率增长率降为27%以下,说明驾驶员开始恢复舒适状态。

如图8所示,在隧道入口前70 m,驾驶员心率增长率低于27%,在隧道前98 m,心率增长率达到最小值,为23.2%。随后,驾驶员心率增长率开始增大,直至洞内8 m,增大至35.95%;随着隧道纵深的增加,心率增长率在25%～28%范围内呈现不同幅度的波动;在隧道出口前98 m,心率增长率开始增大,在出口达到峰值,为31.76%,驶出隧道后88 m,心率增长率趋于稳定。

图8 心率增长率与距离的关系图(隧道路段)

在驶入、驶出桥梁以及驶入、驶出隧道的过程中,驾驶员心率增长率都是呈现先增大后降低的趋势。在桥梁起终点、隧道出入口的心率增长率出现波峰,心率增长率达到最大,在出入口附近心率增长率高于27%,驾驶员处于紧张状态,所以,从心率增长率来看,在这些路段同样存在安全隐患。

通过散点图分析桥隧过渡段上驾驶员心率增长率与速度的关系,如图9所示,由于驾驶员行车存在加减速的过程,不同速度驾驶员的心率增长率变化不同。驾驶员在驶出桥梁后速度会有所增加,心率增长率会随着速度的增大而增大(图中绿色散点);当驾驶员注意到隧道后,速度逐渐降低,心率增长率有小幅度降低;驾驶员越来越接近隧道入口时,速度虽然减小,但由于驾驶员驶入隧道,受到 “黑洞效应”影响,心率增长率开始增加(如图中黑色散点)。因此为反映桥隧过渡段区段整体驾驶员心生理参数的变化情况,建立相关数学模型,公式如下:

y2=-3.158 62V+0.021 89V2+137.960 42

(11)

式(11)的相关系数R=0.748 78,通过F检验。

图9 心率增长率与速度的关系曲线

4 桥隧过渡段最小安全间距设置

根据心率增长率变化规律,将在桥梁前驾驶员心率增长率增加过程车辆所行驶的距离取为L′q1,在桥梁后心率增长率降低过程车辆所行驶的距离取为L′q2,作为驾驶员适应行车环境的最小安全距离。在隧道前心率增长率增加过程车辆所行驶的距离取为L′s1,在隧道后心率增长率降低过程车辆所行驶的距离取为L′s2,作为驾驶员适应行车环境的最小安全距离。

结合速度、心率增长率的变化趋势,确定桥隧路段不同连接形式下的安全间距。下面对2种不同连接形式分别讨论。

1) 隧-桥-隧路段

在隧道-桥梁-隧道相连接时,如图10所示,桥隧过渡段的间距公式如下:

(12)

(13)

(14)

其中:t为驾驶员的反应时间,取2.5 s;a为加速度,取2 m/s2;v1为桥梁前初始行车速度;v3为在桥梁上行驶的速度;v5为驶出桥梁恢复后的速度;v6为驶入隧道前的初始速度;v8为在隧道行车的速度;v10为驶出隧道恢复后的速度;y1、y3、y5、y6、y8、y10分别为v1、v3、v5、v6、v8、v10对应的心率增长率。

隧-桥-隧相连接时,基于速度、心率的隧道出口、桥梁入口安全距离取最大值,桥梁入口与隧道出口的间距之和作为过渡段间距L1;基于速度、心率的桥梁出口、隧道入口安全距离取最大值,桥梁出口与隧道入口的间距之和作为过渡段间距L2。

2) 桥-隧-桥路段

在桥梁-隧道-桥梁相连接时,如图11所示。桥隧过渡段的间距公式如下:

(15)

其中:t为驾驶员的反应时间,取2.5s;Ls1、Ls2、Lq1、Lq2、L′s1、L′s2、L′q1、L′q2的计算公式如式(13)、(14)所示。

桥-隧-桥相连接时,基于速度、心率的桥梁出口、隧道入口安全距离取最大值,桥梁出口与隧道入口的间距之和作为过渡段间距L3。基于速度、心率的隧道出口、桥梁入口安全距离取最大值,桥梁入口与隧道出口的间距之和作为过渡段间距L4。

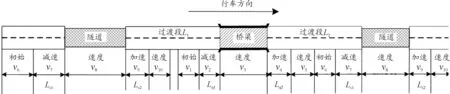
图10 隧-桥-隧路段示意图

图11 桥-隧-桥路段示意图

规范[21]对过渡段进行了规定,将规范值与公式计算结果对比,如表3所示。

表3 过渡段长度规范值

通过式(12)—(14)计算得到设计速度100 km/h时,L1、L4的最小值为123.32 m,L2、L3的最小值为141.04 m,大于规范值结果,说明更安全。综合考虑过渡段的安全距离,建议L1、L2、L3、L4的值取整,最小为145 m。

5 结论

在桥梁路段,驾驶员心率增长率随着速度的增加而增大;当驾驶员注意到隧道后,速度逐渐降低,心率增长率有小幅度降低;在驾驶员接近隧道入口时,驾驶员心率增长率随着速度的减小开始增加。

综合考虑了速度与心率增长率变化规律,提出桥隧不同连接形式的过渡段的安全间距的计算方法,确定了过渡段的最小安全间距值。