三相LCC无线充电系统变频软开关能效优化研究
2023-04-11周成虎黄明明库永恒刘宏伟陈素霞
周成虎,黄明明,库永恒,刘宏伟,张 洋,陈素霞
(1.河南工程学院 电气信息工程学院, 郑州 451191;2.国网河南省电力公司驻马店供电公司, 河南 驻马店 463000;3.河南工程学院 计算机学院, 郑州 451191)

国内外学者针对使用LCC补偿电路的单相感应电能传输系统的研究比较多,其轻载同样比重载的效率低。文献[5-7]中记载的LCC感应电能传输系统的轻载效率普遍低于重载效率10%以上。对于数千瓦甚至更高功率的电路,不能满足于效率大于90%的表面现象,需要重点关注数百瓦特以上的功率究竟损耗在哪些元器件上。电动汽车感应无线充电时负载容量大且变化范围宽[8],如果轻载时逆变器开关管硬开关关断,将使开关管急剧发热并可能导致器件损坏。因此,要重点讨论在轻载边界处开关管通断是否处于软开关状态。
采用LCC补偿电路的单相感应电能传输系统,通过补偿网络参数配置和工作频率设置可以实现恒压或恒流特性,且易于实现零电压开关,可降低开关损耗[9-12]。国玉刚等[11]对LCC-S型无线电能传输系统进行优化配置,给出了多种工作模式,采用变频控制方法提高系统效率,使轻载效率提高到86.1%以上。此外,该文献阐述了在有些工作模式下补偿元件电压是输入电压的数十倍,因此在传输特性优化过程中需要关注补偿元件的谐振电压和谐振电流。吴理豪等[13]和孙淑彬等[14]发现,变频控制较为复杂,且频率变化范围需满足相关标准,移相控制可能带来硬开关、直流电压纹波大等问题。对于大功率充电电路,在开关管的过渡过程中出现短暂的硬开关状态会降低开关管的使用寿命,严重时会导致开关管损坏。
基于LCC衍生补偿电路的单相逆变器结构采用最优负载追踪的控制方法[15-17],在避免轻载效率过低方面取得了丰硕成果。但当这些结构应用于大功率和宽负载范围的电动汽车无线充电电路时,其轻载效率仍难以达到理想程度。
上述研究成果表明,采用变频虽然可以提高LCC补偿电路的感应电能传输系统的轻载效率,但是要实现暂态过程、轻载状态均始终处于软开关状态且达到理想的效率,尚需进一步努力。为了进一步提高传输效率和传输功率,在文献[1-2]的基础上,本文基于LCC补偿的三相感应电能传输系统的变频定占空比控制策略,归纳得到软开关频带优化与阻抗匹配方法。推导出复合谐振网络阻抗及其谐振频率、原边线圈及其补偿电路的固有阻抗及其谐振频率、副边线圈及其补偿电路的固有阻抗及其谐振频率的计算式;总结3种谐振频率和开关频率之间的配合原则,以此优化开关管的软开关频率范围,依据该关系并结合仿真确定元件参数;使用变频方法匹配阻抗,在负载变化时调节传输功率并提高效率。电路分析和仿真结果验证了该电路在开关频率范围内和变频过程中均具有强鲁棒性的自然软开关切换能力。
1 LCC补偿的三相感应电能传输系统与频率匹配分析
设计的LCC补偿的三相感应电能传输系统如图1所示。该拓扑结构由电感L1、三相方波逆变器、磁耦合机构与LCC补偿电路和整流电路构成。三相逆变器将直流电转化为高频交流电,由磁耦合机构与LCC补偿电路传输到副边电路。
1.1 复合谐振网络阻抗的计算方法
图1副边所示的三相倍压整流电路具有电流源性质,可等效成3个独立电流源的叠加。在电流is31、is32和is33正半周时分别流经二极管D1、D2、D3,共同流经电容C4;负半周时分别流经二极管D4、D5、D6,共同流经电容C5。电流is31、is32、is33的平均值分别用Is31、Is32、Is33表示,则IDC=(Is31+Is32+Is33)/2,当开关管S1~S6的占空比相同时,IDC=3Is31/2。

(1)
因为三相电路元件选用相同的参数,图1所示的三相磁耦合机构与补偿电路结构完全对称,电容Cp31=Cp32=Cp33,Cs31=Cs32=Cs33,C1=C2=C3,可将磁耦合机构以后的电路等效为三相三角形负载Z31、Z32和Z33,且Z31=Z32=Z33,等效电路如图2所示。
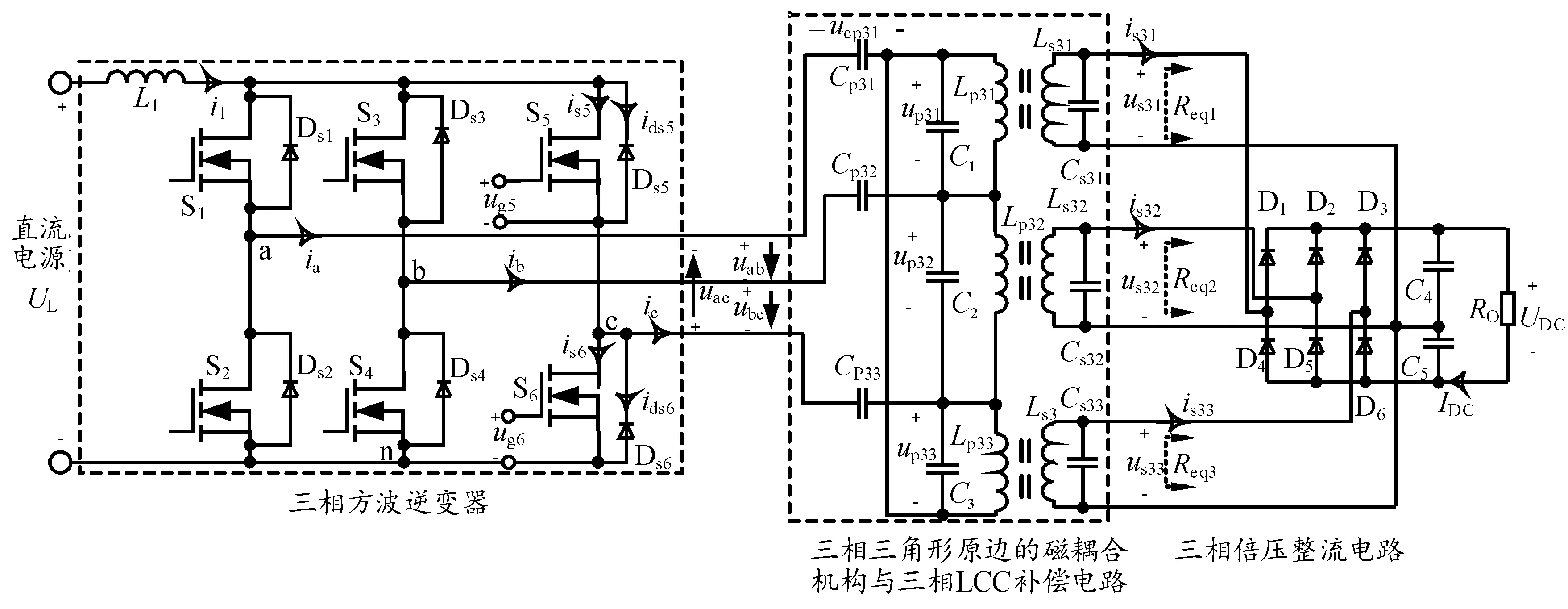
图1 LCC补偿的三相感应电能传输系统电路图
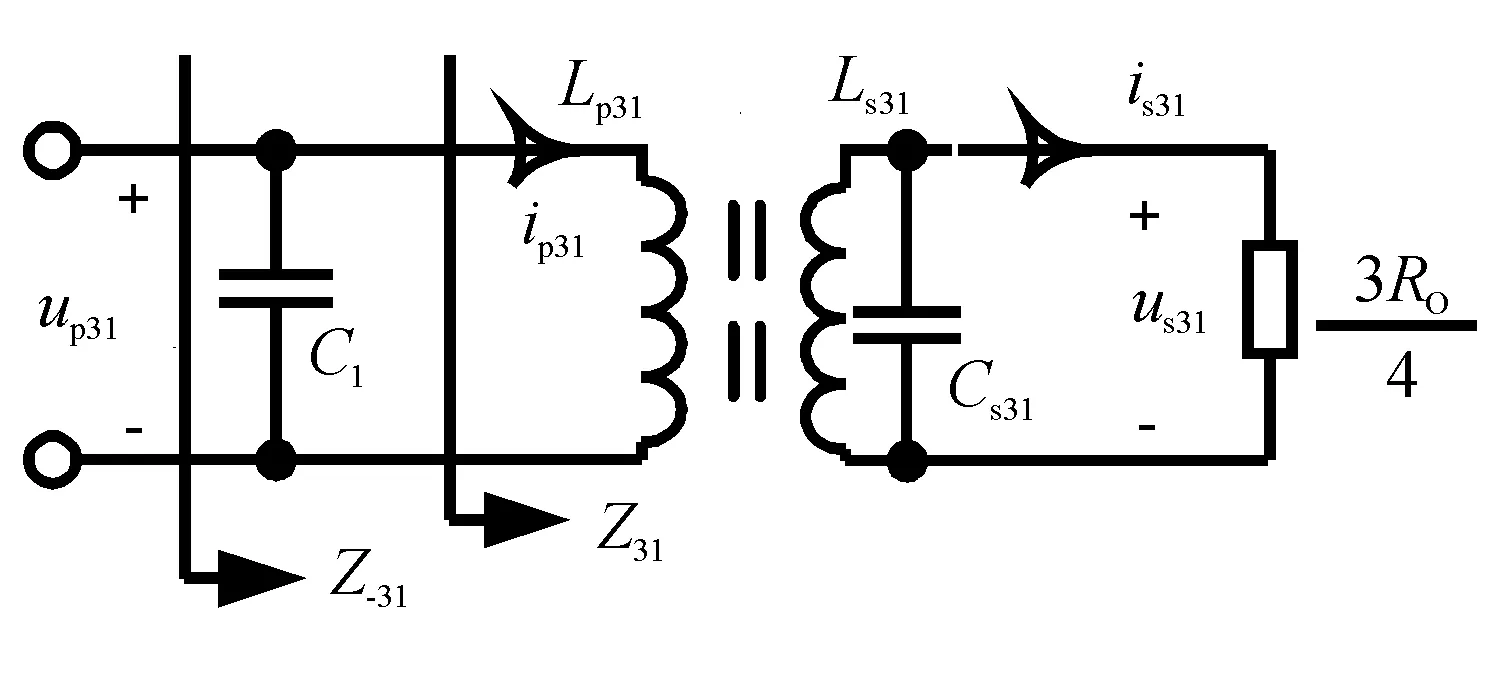
图2 磁耦合机构与补偿电路的等效电路
根据图2和表达式(1),得到副边回路阻抗Zr31(jωT)为:
Zr31(jωT)=
(2)
其中:rs31为电感Ls31的内阻,ωT为开关频率。根据图2和表达式(2),得到阻抗Z31(jωT)为:
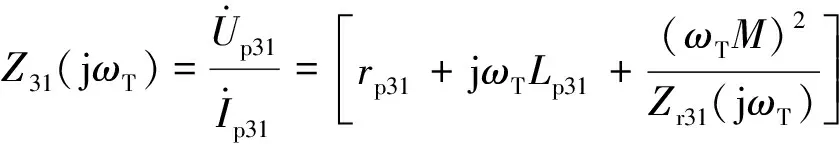
(3)

图2所示的等效三角形均衡负载Z31(jωT)、Z32(jωT)和Z33(jωT)分别与C1、C2、C3并联,得到三角形阻抗ZΔ31(jωT)、ZΔ32(jωT)、ZΔ33(jωT)。其中三角形阻抗ZΔ31(jωT)的表达式为:
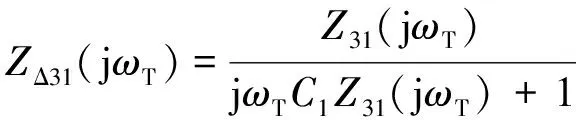
(4)
将其分别转化为星形负载Z11(jωT)、Z12(jωT)和Z13(jωT),其中:
(5)
图2所示的三相逆变电路三角形均衡负载转化为星形负载后,星形负载中心点可以看作是输出的零线,三相逆变器可以等效为3个独立半桥的拓扑结构。其中,等效的A相半桥电路如图3所示。
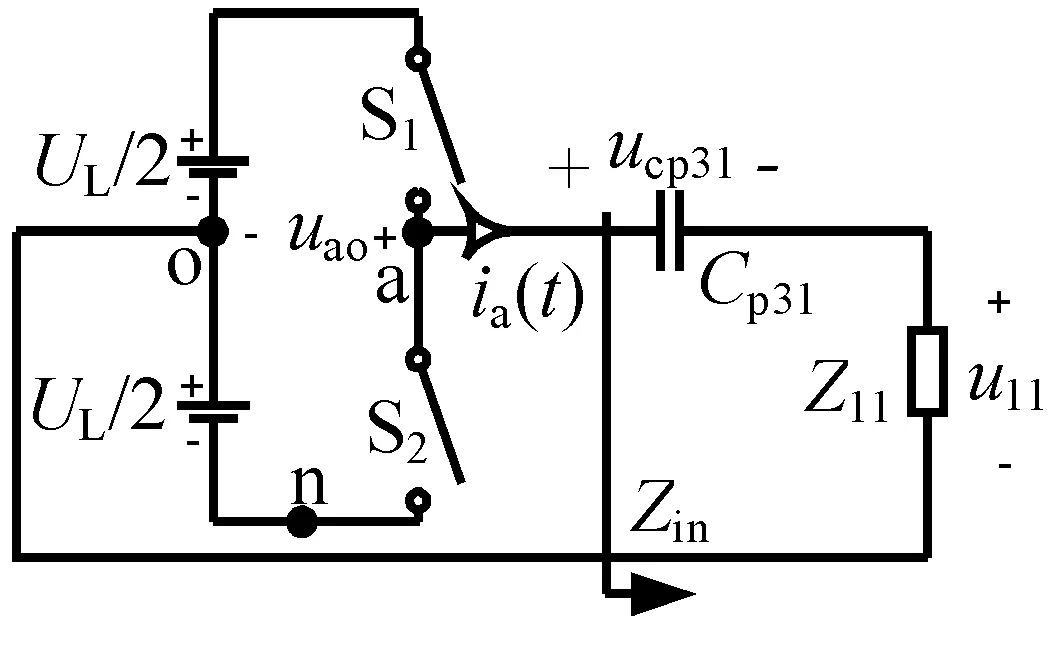
图3 等效的A相半桥电路
从输入电压uao到输出电压u11的传递函数为:
(6)
根据表达式(1)—(6),可以得到包含原副边磁耦合机构与补偿电路的复合谐振网络阻抗Zin的表达式为:
(7)
1.2 3种谐振频率的计算方法
由于三相逆变器、原边谐振电路和副边谐振电路前后级联,系统具有3种谐振频率:复合谐振网络频率fT、原边线圈及其补偿电路的固有谐振频率fp和副边线圈及其补偿电路的固有谐振频率fs。列出3种谐振频率的计算方法如下:
1) 求解复合谐振网络阻抗Zin对应的复合谐振网络频率fT。首先对阻抗Zin求虚部Im(Zin)可得:
(8)
令虚部Im(Zin)=0 Ω,可推导出复合谐振网络频率fT的表达式。因该表达式过长,此处略去。
2) 求解原边线圈及其补偿电路的固有谐振频率fp。在不考虑电磁耦合的情况下,可将原边谐振电路看作是带通滤波器,原边固有阻抗Zp为:
(9)
从式(9)推导得到原边固有阻抗Zp的虚部Im(Zp):
(10)
使用Maple软件,令Im(Zp)为0,可推导出原边固有谐振频率fp的解fp1和fp2:
(11)
3) 求解副边线圈及其补偿电路的固有谐振频率fs。在不考虑电磁耦合的情况下,可将副边谐振电路看作低通滤波器,副边线圈及其补偿电路的阻抗Zs的表达式为:
(12)
令Zs的虚部为0,得到副边线圈及其补偿电路的固有谐振频率fs的解:
(13)
1.3 软开关频带优化与阻抗匹配方法
因为副边谐振电路被看作是低通滤波器[19],所以应满足条件:
fvmax≤fs≤ 2·fvmin
(14)
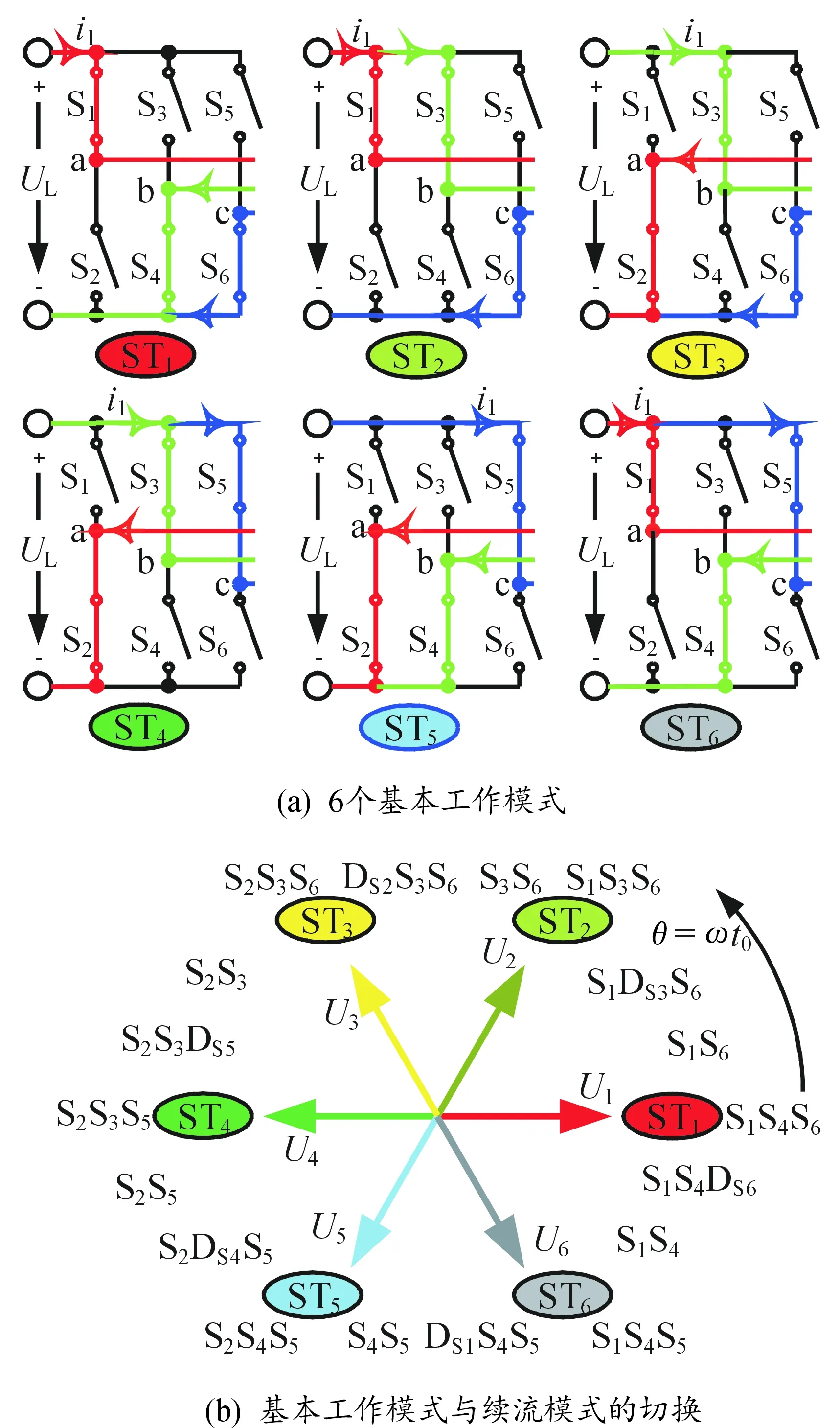
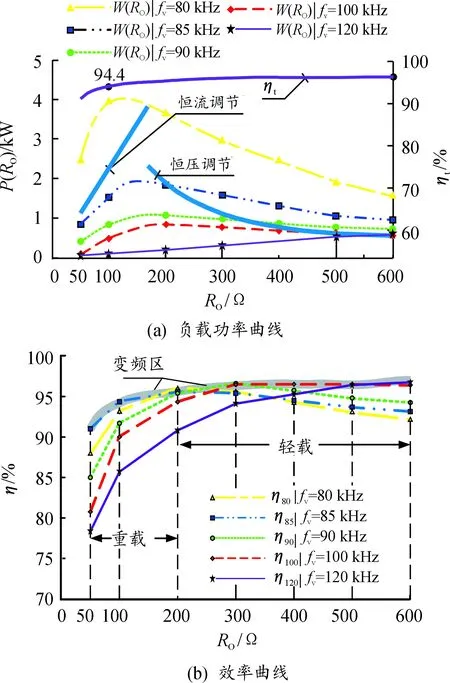
其中:fvmin和fvmax分别表示最小和最大开关频率。因为原边谐振电路可看作是带通滤波器[19],频率fp具有2个正实根fp1和fp2,设fp1 fp1≤fvmax≤fs≤ 2·fvimn (15) 如果将逆变器的开关管等效为理想开关,当fv=fT时,系统可以获得最大传输功率。由于实际的开关管存在开通上升时间和关断下降时间,当fv接近fT时,开关管脱离软开关状态,开关过程中瞬时功率达到数千瓦特以上。设定开关管的开关频率fv在80~100 kHz调节,则fv应高于复合谐振网络频率fT,以使阻抗Zin呈弱感性[20-21]。依据上述分析,结合电路仿真[22-24],当fT≤ 0.95fv时,开关管能保持软开关状态。据此设定并留出余量,可得fT与fv满足关系式: fT≤0.92·fvmin (16) 已知fvmin=80 kHz,依据关系式(16)可计算得:fT≤73.1 kHz。依据关系式(14)—(16)设定副边固有谐振频率fs≈1.5·fvmin,选择的副边参数元件如表1所示。将表1的元件参数代入表达式(13),计算出fs=121.7 kHz。由于原边和副边谐振电路可看作是滤波器,因此电路的通频带介于fp1和fs之间。 要使fT的频率范围满足关系式(15)、(16)的要求,必须选择合适的元件参数。具体做法是先令阻抗Zin的虚部Im(Zin)=0 Ω,得到频率fT的表达式。选取元件参数代入该表达式,当负载电阻RO从40 Ω增大到1 kΩ时,使复合谐振网络频率fT的主谐振频率fT1的频率范围从73.1 kHz降低到71 kHz;分别计算出复合谐振网络频率fT的次谐振频率fT2,计算结果如表2所示,此处忽略另外4个复数谐振频率。在电路中起到主要作用的是主谐振频率fT1,次谐振频率fT2在2个滤波器的范围之外,因此在本文中忽略fT2的影响,将复合谐振网络频率fT等同于主谐振频率fT1,即fT=fT1。使用上述方法选择的原边元件参数如表1所示。将表1的参数代入表达式(11),计算出原边固有谐振频率fp分别为fp1=71.8 kHz;fp2=183.8 kHz。 表1 副边元件参数 表2 不同负载电阻对应的频率fT的谐振频率 将原边谐振电路看作是带通滤波器,将副边谐振电路看作是低通滤波器。复合谐振网络频率fT既要略低于开关频率fv,又要在滤波器的通频带之内,才能获得较大的传输功率。4种频率的特性示意图如图4所示。此外,从上述分析可知,复合谐振网络频率fT的主谐振频率主要取决于原边固有谐振频率fp1。副边固有谐振频率fs主要影响滤波效果。如果开关频率fv上下限不能落入频率fp或频率fs的通频带内,将直接影响滤波效果。 图4 4种频率的特性示意图 采用Pspice仿真得到频率fT与负载功率P(RO)的对应关系如图5所示,负载功率P(RO)采用对数坐标。从图5可知,在fv≈85 kHz附近,当开关频率fv降低,负载功率P(RO)上升,这是控制系统设计的基本原则和理论依据。若复合谐振网络频率fT与开关频率fv配合偏差过大,则会造成传输功率过小或脱离软开关状态等后果。 在分析工作模式的基础上,阐述逆变器开关管工作在自然软开关状态且具有较强鲁棒性的原理。 图5 频率fT与负载功率P(RO)的对应关系曲线 三相PWM逆变器的工作模式如图6所示。图6(a)为6种基本工作模式ST1~ST6,每种基本工作模式均有2个上桥臂或2个下桥臂同时导通,相位角θ沿顺时针方向变化如图6(b)所示。 图6 三相PWM逆变器的工作模式示意图 将电压ua、ub、uc用合成矢量表示,基本工作模式ST1~ST6对应6个空间矢量U1~U6。其中,空间矢量U1、U2的计算表达式为: (17) (18) 按照上述方法依次可求出空间矢量U1~U6的值。 以工作模式ST1向工作模式ST2切换为例,分析软开关的工作原理。在工作模式ST1,上桥臂开关管S1导通,下桥臂开关管S4和S6同时导通,如图7(a)所示。此状态电源电流i1流过开关管S1、电容Cp31,然后分两路,一路经阻抗ZΔ31、电容Cp32、开关管S4回流到电源负极;另一路经阻抗ZΔ33、电容Cp33、开关管S6回流到电源负极。两路并联电压相等,开关管S4和S6的压降均接近0 V。此过程中电容Cp31电压左正右负、电容Cp32、Cp33的电压右正左负。 图7 工作模式ST1向ST2切换的过程示意图 工作模式ST1向ST2切换要经过两个过程: 1) 第一过渡过程如图7(b)所示。在此过程中开关管S4截止,S4漏极和源极两端电压略有上升即导致两路电压不再相等,因此开关管S4的电流迅速归零并在零电流状态关断。电流i1经开关管S1、电容Cp31、阻抗ZΔ33、电容Cp33和开关管S6构成供电回路。 2) 第二过渡过程如图7(c)所示。在此过程中电容Cp31电压左正右负、电容Cp32的电压右正左负,在开关管S1、电容Cp31、阻抗ZΔ31、电容Cp32和二极管Ds3构成的续流回路中,二极管Ds3导通续流,使即将开通的开关管S3处于零电压软开关开通状态。另外,此过程还包括电流i1经开关管S1、电容Cp31、阻抗ZΔ33、电容Cp33和开关管S6构成的供电回路。因为电容Cp31在续流回路中处于放电状态,在供电回路中处于充电状态,所以二极管Ds3导通续流时间长。只要二极管Ds3导通续流,则开关管S3的开通电压始终保持在0 V,因此开关管S3在软开关状态下闭合具有强鲁棒性。为进一步分析实现自然软开关状态的工作原理,对图1所示的电路进行全系统仿真。设置输入电压UL=220 V,负载RO=100 Ω,仿真结果如图8所示。 图8 仿真结果 在t0~t1阶段,开关管S1、S4、S5导通,工作模式为ST6。 在每个开关管S1~S6关断过程中,电流ia、ib、ic的波形迅速降至0 A。在每个开关管S1~S6导通过程中,与其反并联的二极管导通续流,使开关管处于零电压软开关开通状态。当频率满足式(15)时,开关管具备自然软开关条件。 仿真结果证明,当所有开关管S1~S6的占空比均为40%~42%,开关管的开关频率fv在80~120 kHz调节,且负载电阻RO在50~600 Ω条件下,开关管工作在软开关状态,鲁棒性最强。为简化分析,设定所有开关管S1~S6的占空比均为41%。值得注意的是,变频控制既不需要复杂的控制方法,也不需要增加额外的谐振电路或控制电路。 根据图1搭建的实验电路如图9所示。使用表1的元器件参数,开关管S1~S6的频率fv=80~120 kHz,型号为C2M0025120D;电源输入直流电压UL=220 V;L1=10 μH。 图9 实验电路实物 当选用负载箱电阻RO=100 Ω,开关频率fv=84 kHz,实验波形如图10所示。电路在每次基本工作模式切换过程中,电流ia、ib、ic在第一个过渡阶段瞬间下降到0 A,具备开关管零电流关断的典型特征。 图10 实验波形 从图10可知,在工作模式为ST6向ST1切换的第一个过渡阶段,电流ic下降到0 A,在电流ic为0 A的过程中完成开关管S5的关断过程。因为电流is5=0 A,开关管S5断开时的瞬时功率p5=ucn·is5=0 W,所以开关管S5是软关断。 在工作模式为ST6向ST1切换的第二个过渡阶段,二极管Ds6续流,其电流ids6具有足够长的时间,能保证开关管S6在零电压软开关状态开通。 因为三相逆变器的横向换流具备软开关的鲁棒性,纵向换流具有足够的死区时间且换流瞬间电源电流i1始终具有导通通道,所以相比常用的单相逆变器换流具有明显的优越性。 电动汽车电池充电过程包括恒流和恒压充电阶段。恒流充电阶段负载较重,恒压充电阶段负载较轻。 变频控制的负载功率曲线如图11(a)所示。负载功率W(RO)随着开关频率fv的增加而下降,当开关频率fv固定,随着负载RO电阻值的增大(由重载到轻载),负载功率先升后降。 变频控制的效率曲线如图11(b)所示。效率曲线峰值随着开关频率和负载电阻的变化而变化。通过对比开关频率fv分别等于80、85、90、100、120 kHz的效率曲线可知,在直流电源UL恒定的条件下,每种频率的传输效率峰值对应不同的负载电阻。当负载电阻RO在170 Ω以下,开关频率fv等于85 kHz时,系统的传输效率比较高;当负载电阻RO在200 Ω左右,开关频率fv等于80 kHz时,系统的传输效率较比较高;当负载电阻RO在300 Ω左右,开关频率fv等于90 kHz时,系统的传输效率比较高;当负载电阻RO在400 Ω左右,开关频率fv等于100 kHz时,系统的传输效率比较高;当负载电阻RO在500 Ω以上,开关频率fv等于120 kHz时,系统的传输效率比较高。当直流电源UL改变,每种频率的传输效率峰值对应负载电阻值也会相应变化。 图11 变频控制的负载功率和效率曲线 根据上述分析,重载阶段开关频率为80~85 kHz时效率较高,用降频增大传输功率的方法实现恒流调节;轻载阶段轻载阶段开关频率为90~120 kHz时效率较高,用升频方法实现恒压调节。根据负载功率的需求选择合适的开关频率,使负载效率维持在较高的水平。 设定负载电阻50 Ω≤RO≤200 Ω为重载阶段,负载电流IDC=4.77 A,随着RO电阻值的增大,负载功率增大,开关频率fv从85 kHz向80 kHz调节,传输功率从1.14 kW上升到3.87 kW。当重载阶段负载RO=100 Ω,fv=84 kHz,从直流电源UL到负载RO的传输效率为94.4%。 设定负载电阻200 Ω 图1给出的电路系统中采用直流电源供电,供电系统是交流电源,通常使用功率因数校正电路将交流电转化成直流电。因为三相逆变器工作范围大,所以工程应用采取2种方法相结合调节传输功率和效率:第1种方法是论文给出的方法;第2种方法是在功率因数校正环节调整传输电压UL。在减小频率范围的条件下,恰当的调节电压UL可以改变负载和效率的对应曲线,进一步提高重载或轻载的传输效率。限于篇幅,第2种方法不展开论述。 开关频率对应的电压特性如图12所示。图12(a)和(b)示出原边电容电压ucp31和原边线圈电压up31的峰值Ucp31、Up31,其波形为准正弦波;图12(c)示出副边线圈电压us1的峰值Us31,其波形为交流梯形波;图12(d)示出负载直流电压UDC。从图12可知,轻载阶段提高开关频率可以使原边谐振元件的电压峰值Ucp31、Up31显著下降,同时用于传输有功功率的副边线圈电压峰值Us31和负载直流电压UDC在轻载阶段(负载电阻200 Ω 与文献[11]中LCC型单相无线电能传输系统相比,在相同传输功率条件下,三相系统谐振元件的电压应力下降到单相无线电能传输系统的1/3以下。降低谐振元件的电压应力的另一个显著优点是可以降低谐振元件的额定耐压值,有利于提高功率密度。 图12 开关频率对应的实验电压特性曲线 1) 归纳得到软开关频带优化与阻抗匹配方法。将原边谐振电路看作是带通滤波器,将副边谐振电路看作是低通滤波器。将复合谐振网络的主谐振频率设置为略低于开关频率且在滤波器通频带的合理位置,以获得较高的效率和较大的传输功率。 2) 采用LCC补偿电路和三相逆变器配合,在换相过程中能同时产生供电通道和续流通道,供电通道为续流通道提供较长时期的续流能量。这种续流方式是逆变器开关管在开关频率和负载范围内自动实现零电流关断和零电压导通的关键因素。 3) 利用感应耦合传输系统的选频特性选择合适的传输功率,优化传输效率。重载阶段用降频方法增大传输功率,轻载阶段用升频方法降低传输功率和原边谐振环流,不需要额外的谐振电路或复杂的控制方法。相比文献[2]中的参数设计方法,轻载效率提升约3%~5%,进一步简化了电路结构。


2 工作模式与软开关切换原理分析
2.1 基本工作模式分析
2.2 强鲁棒性的自然软开关切换工作原理
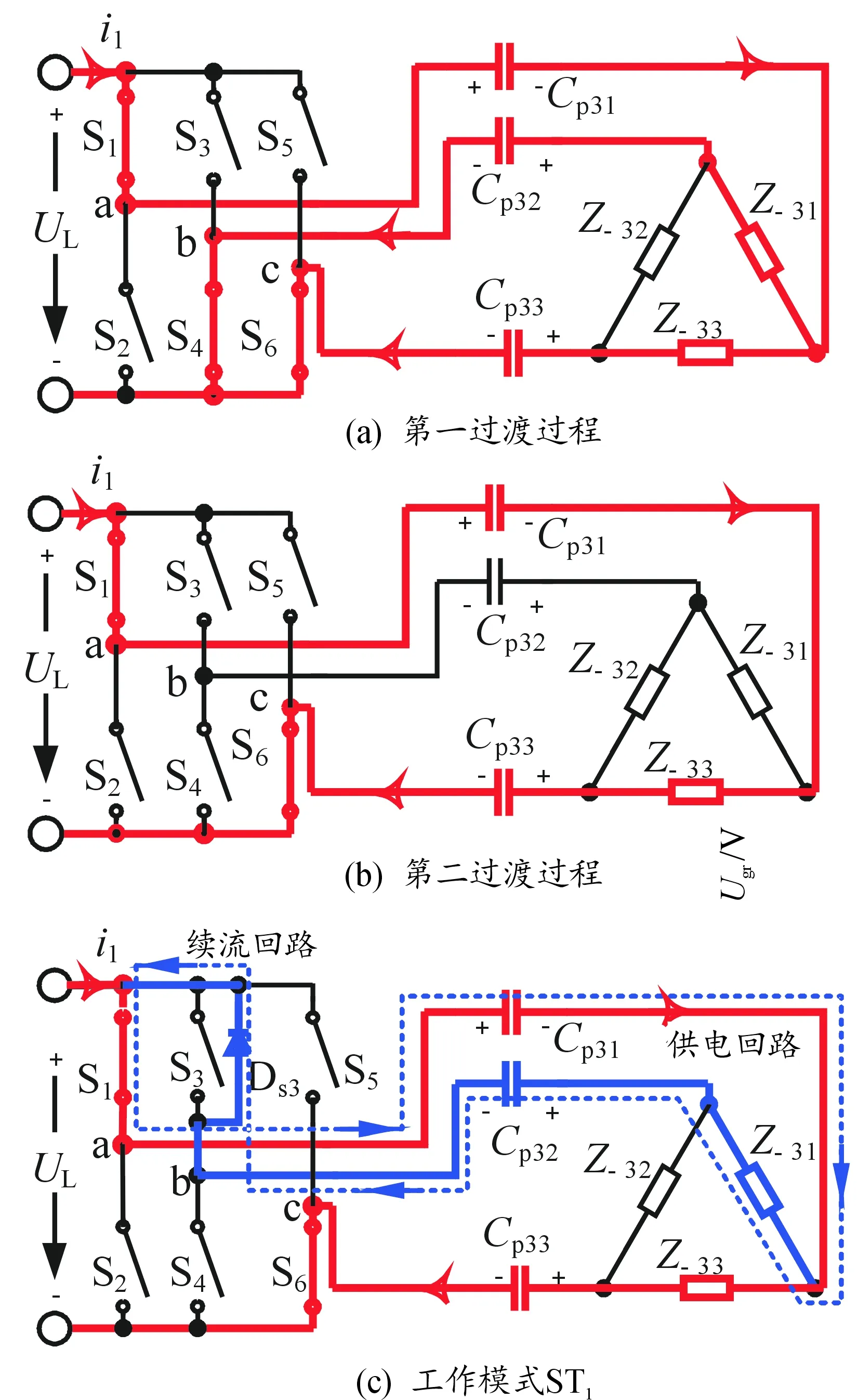
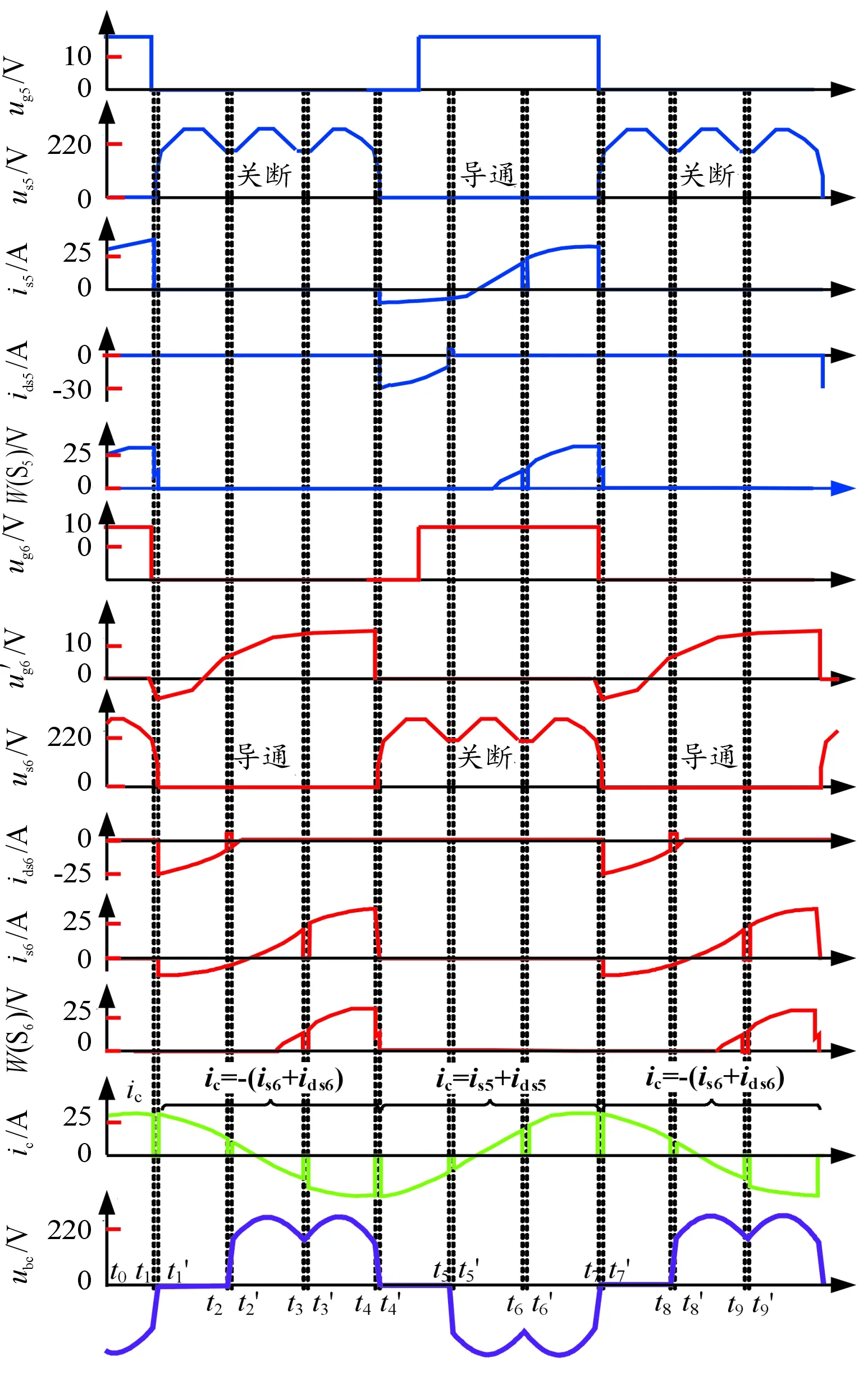

3 实验结果

3.1 软开关特性实验结果
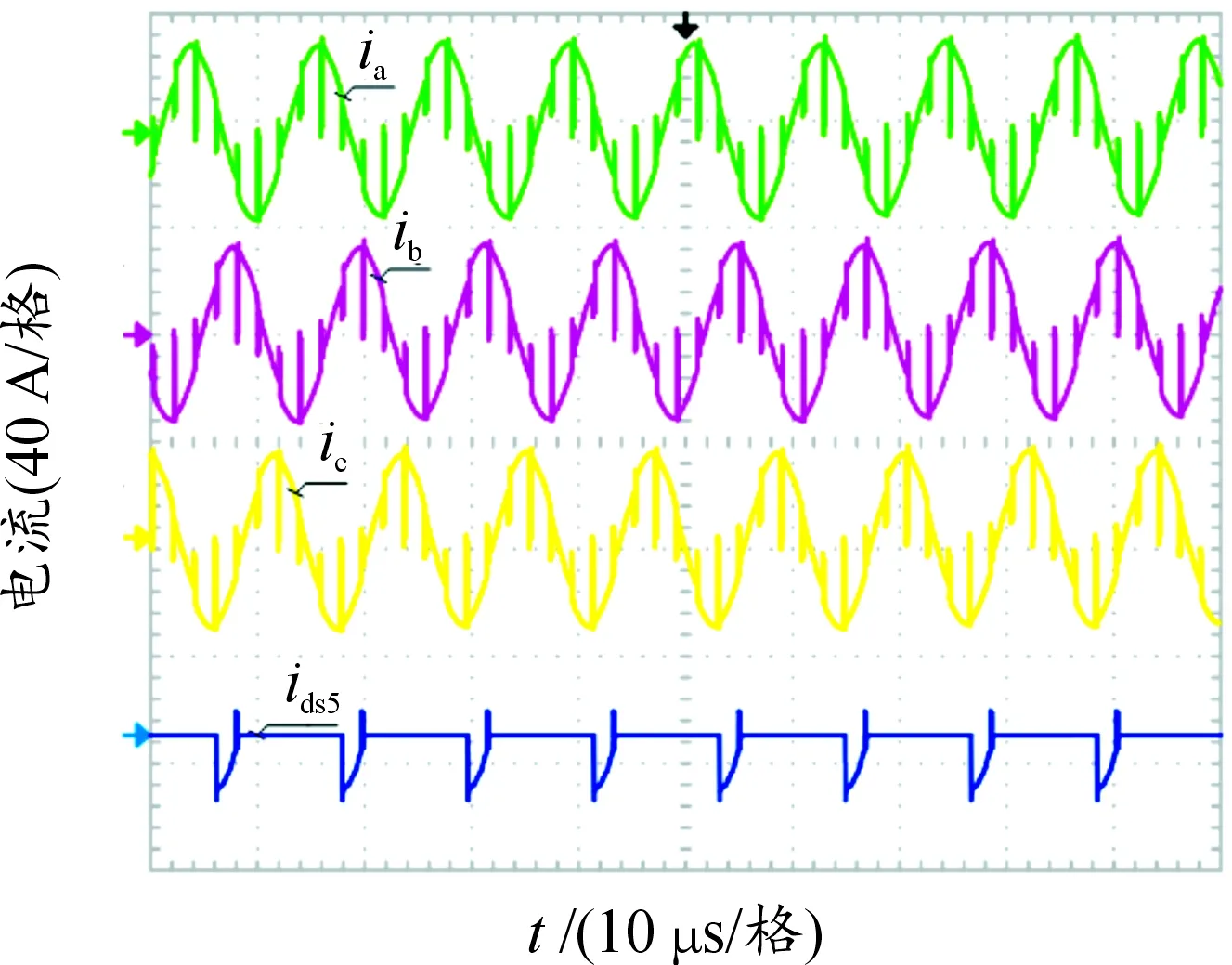
3.2 变频特性实验结果
3.3 开关频率对应的电压特性

4 结论
