融合FCM-RBF的短时交通拥堵状态预测模型

2023-04-11张生瑞连江南焦帅阳

重庆理工大学学报(自然科学) 2023年3期

关键词：交通量交通流聚类

张生瑞,连江南,焦帅阳,周备

(1.长安大学运输工程学院, 西安 710064;2.河南城建学院土木与交通工程学院, 河南平顶山 467036)

随着智能交通系统的发展,交通拥堵预测再次成为当前的研究热点。交通拥堵一般可分为常发性拥堵和偶发性拥堵。研究表明,常发性拥堵占城市道路网络所有拥堵时刻的85%左右[1],对交通系统产生了较为不利的影响。

对常发性交通拥堵路段的状态预测可分为长时预测与短时预测。短时交通拥堵状态预测是基于交通流参数的短时交通拥堵状态识别,具有更高的预测精度和实用性。因此,基于常发性交通拥堵路段的短时交通拥堵状态预测具有更高的现实意义和可操作性。

交通拥堵状态预测分为两步,一是从历史数据中识别不同的交通状态,并划分不同的状态区间;二是针对交通流参数的预测,并与划定的拥堵状态区间比对,确定该状态属于何种拥堵水平。

交通拥堵状态的识别本质上属于分类问题,其方法包含传统的交通流理论方法以及数据驱动方法[2]。其中,数据驱动方法注重模型的应用价值和算法研究,是近年来的研究重点。王来军等[3]通过广义径向基函数神经网络的优化算法建立城市道路交通拥堵度的计算模型,该模型可获得拥堵点的位置和发生时刻。罗向龙[4]采用支持向量机(support vector machine,SVM)算法识别带噪声的交通流状态。Fotouhi等[5]提出基于K均值(K-means)聚类的交通状态算法,并评估了不同聚类数量的聚类结果。袁立罡等[6]分析了特征参数与交通流相态演化规律,提出基于遗传期望最大化模糊聚类算法的交通状态识别方法。张心哲等[7]提出基于霍夫变换和模糊C均值(Fuzzy C-means,FCM)聚类算法的交通状态识别方法,其中FCM聚类方法用于非畅通交通流状态的分类。Cheng等[8]对传统FCM聚类算法进行了模糊隶属函数改进和样本加权处理,通过对该方法与SVM算法、K近邻(K-nearest neighbors,KNN)搜索算法、传统FCM聚类算法等的对比,该算法在分类准确度上体现出较大优越性。交通流状态具有模糊性、不确定性等特点,不同交通状态之间没有明确界限,且不同出行者对交通拥堵程度的主观感受不同,因此,采用基于模糊聚类原则的算法对交通状态的判别结果更符合实际情况。在现有的模糊聚类算法中,FCM聚类算法最为完善、应用最为广泛,能够处理大规模数据集,具有良好的数据分类效果。

针对交通流参数的预测,陈忠辉等[9]提出了基于FCM聚类和随机森林算法的短时交通状态预测模型。林浩等[10]提出一种基于SVM和模糊综合评价的交通流预测模型。Cai等[11]采用改进的KNN算法实现了对短时交通流的多步预测。吴玲玲等[12]提出一种改进的反向传播(back propagation,BP)神经网络短时交通流预测模型,该模型有效提高短时交通流预测精度。Ai等[13]将模糊逻辑与径向基函数(radical basis function,RBF)神经网络相结合,提出预测交通速度的混合RBF神经网络算法。Chen等[14]提出一种基于改进的RBF神经网络的短时交通流预测算法,并与KNN模型、改进的BP神经网络模型等进行对比,结果表明该模型预测精度较高。短时交通流具有随机性、非线性特性,而RBF神经网络在逼近任意非线性函数、并行化处理信息方面具有明显优势,且收敛速度快,不易陷入局部最优值,能够满足短时交通流预测对时效性、准确性的要求。

FCM聚类算法引入了模糊的概念,能较好表达和处理不确定性问题。RBF神经网络结构简单,训练速度快,具备较强的非线性逼近能力,预测精度较高。但是现有的交通拥堵状态预测模型较少考虑二者的融合预测方法。基于上述分析,本文提出一种融合FCM聚类算法与RBF神经网络的、针对常发性拥堵路段的短时交通拥堵状态预测模型。首先利用FCM聚类算法对历史交通流数据进行聚类划分,用于实现已有交通数据的分类,并为后续交通状态判别提供分类依据;然后利用RBF神经网络预测短时交通流参数,保证交通流预测的实时性和准确性;最后,根据已知交通状态聚类中心来分析预测得到的短时交通流数据所属的交通状态,实现交通拥堵状态预测的目的。本文通过对模型进行实例验证、性能评价并与其他模型进行对比分析,表明了所建立模型的有效性,建立的模型能够为出行者提供可靠有效的短时交通拥堵状况信息。

1 交通数据描述与处理

1.1 数据描述

本文选取的交通流数据源自美国明尼苏达州双子城交通管理中心[15],该中心沿环城高速公路全天实时采集道路中不同地点的交通流数据,采集间隔为30 s。本文选取编号为1007、1006、80的检测器记录的交通流数据,数据累计时长1 080 h,约3 888 000条数据。表1为部分原始数据。

表1 部分原始交通数据

1.2 数据处理

由于原始数据存在缺失数据和异常数据,为保证预测精度,对原始数据进行处理,以满足模型对输入数据的要求,从而提高模型预测精度。数据处理步骤包括:缺失值补全、加和处理、降噪处理和归一化处理。

首先,选用加权平均法对原始数据中的错误及缺失数据进行补全修复,得到包含各个时刻的完整数据集。其计算公式如式(1)所示:

y(t)=a×y(t-1)+

(1-a)×y(t+1)

(1)

式中:y(t)表示t时刻的数据值;a表示加权系数,本文设a=0.5。

原始数据是按照等间隔时段记录的,不能直接用于分析交通拥堵状态。为准确提取交通流数据特征,以5 min作为数据时段划分间隔,即将原始数据每10个为一组进行数据加和,每天合计得到288组数据。

为消除交通流数据中产生的噪声,选用小波变换的数据降噪方法。实际交通流数据为非平稳低频信号,噪声多为高频信号,通过对原始信号进行小波分解,去除高频带上噪声信号对应的小波系数,保留原始信号对应的小波系数,然后对处理后的高频系数和低频系数进行小波重构,获得降噪后的交通流信号数据[16]。降噪前后的部分数据如图1所示。

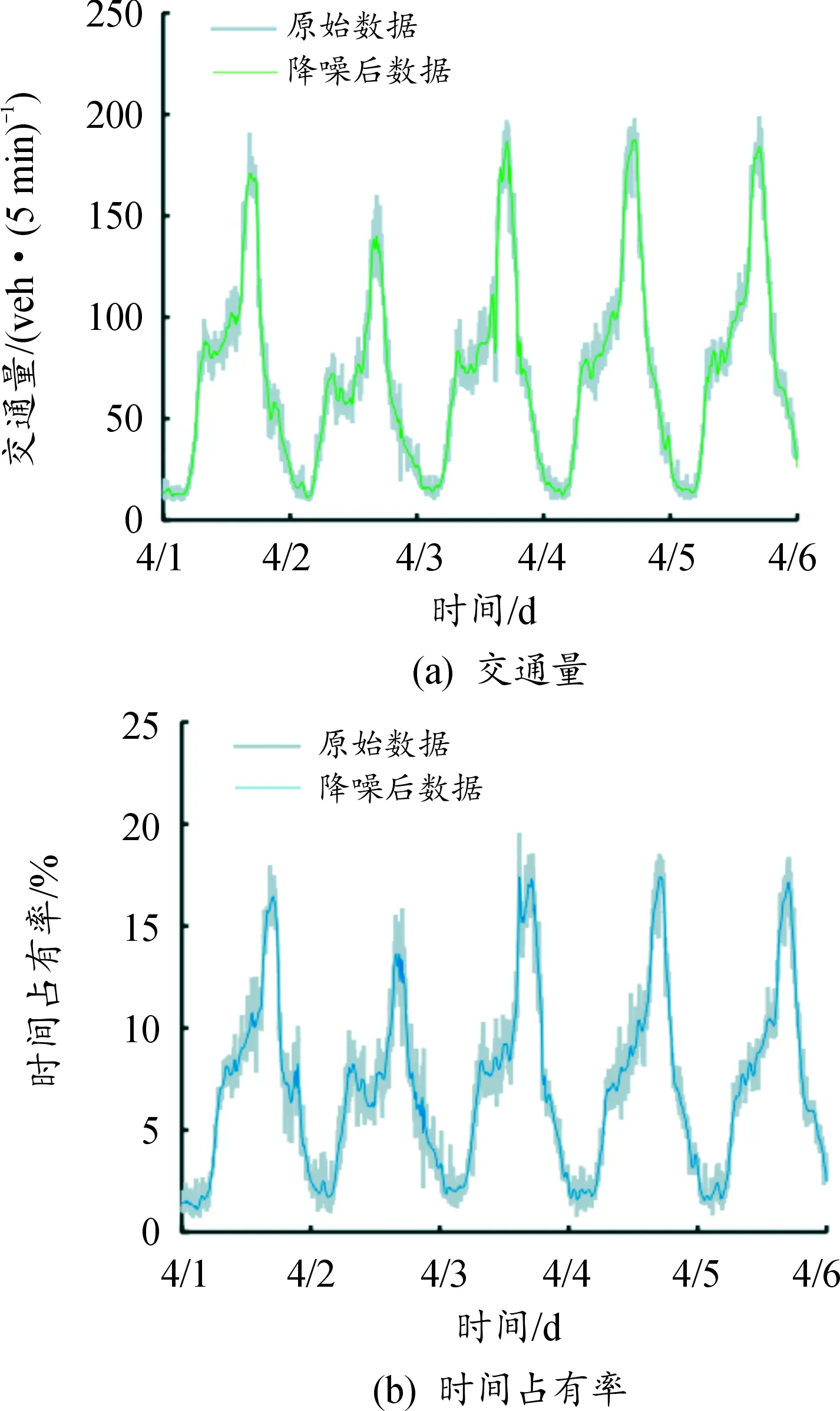
图1 降噪前后的交通量和时间占有率数据

从图1中可看出,经过小波降噪处理,数据变化趋势更加平稳,且降噪前后交通流数据的变化趋势并没有发生改变,更适用于研究交通拥堵问题。

为便于分析不同量纲数据在同一标准下的差异,并缩短模型运算时间,将数据线性映射到 [0,1]区间内,用于模型的训练和预测。然后,对预测数据进行反归一化处理,转换为具有实际意义的交通流数据。

归一化处理的计算公式如式(2)所示:

(2)

反归一化处理的计算公式如式(3)所示:

x=x*(xmax-xmin)+xmin

(3)

式中:x*表示归一化处理后的数值;x表示反归一化处理后的数值;xmax表示原始数据中的最大值;xmin表示原始数据中的最小值。根据交通量和时间占有率的最大值和最小值,对其分别进行归一化处理。

表2为经过预处理后的数据示例。

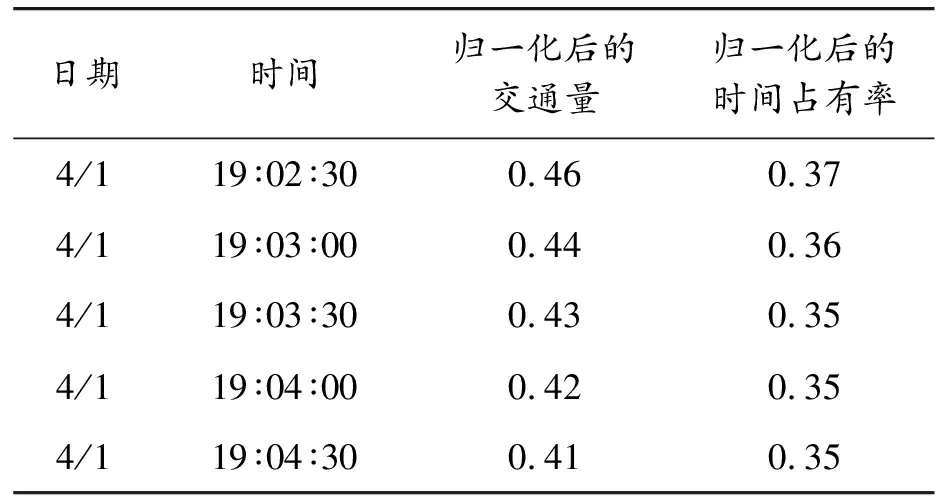
表2 原始交通流的示例数据

对数据进行预处理后,选取90%的数据作为训练数据集,10%的数据作为测试数据集,对模型所作预测结果进行检验。

2 短时交通拥堵状态预测模型构建

本文研究目的是对未来短时交通流参数进行预测并判断其处于何种交通状态。本文重点需要解决2个问题:① 实现对历史数据的聚类;② 实现对未来交通流数据的预测,并将任意一组预测得到的交通流数据划分到相应类别中。

2.1 短时交通拥堵状态预测模型

本文设计的短时交通拥堵状态预测模型计算流程如图2所示。

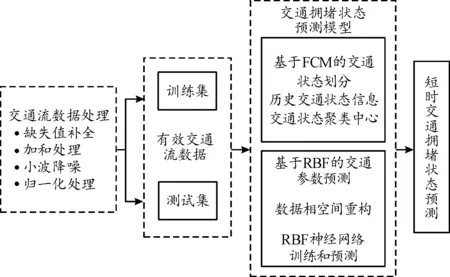
图2 短时交通拥堵状态预测模型计算流程框图

短时交通拥堵状态预测的具体步骤为:

1) 将上一节中预处理后的数据划分训练集和测试集。

2) 利用训练集数据建立交通参数的特征指标矩阵。采用FCM聚类算法在二维空间进行聚类分析,将历史交通流数据划分为5种交通拥堵状态,得到各个时刻对应的状态标签以及不同交通状态对应的聚类中心,为后续交通状态判别提供判别依据。交通拥堵状态划分依据参考《GB/T 33171—2016城市交通运行状况评价规范》[17]。

3) 采用训练集经过相空间重构的交通量和时间占有率数据分别训练2个RBF神经网络模型,通过训练建立输入和输出的映射关系。采用测试集数据预测短时交通流参数。

4) 通过RBF神经网络预测的短时交通量和时间占有率数据,构建预测样本集,计算预测样本集中每个样本点和训练得到的5个聚类中心的欧氏距离,与样本点欧式距离最短的聚类中心所对应的交通拥堵状态即为预测的该样本点的交通拥堵状态。

2.2 交通拥堵状态识别算法

模糊C均值(fuzzy C-means,FCM)聚类算法是一种无监督模糊聚类算法,其核心思想是把样本数据划分成多个模糊簇,同一簇的数据相似性较大,不同簇的数据相似性较小。

给定样本集X={x1,x2,…,xn}⊂Rb,每个样本都具有b个特征指标;将样本集X划分为c个模糊簇,每个模糊簇含有1个聚类中心。FCM的目标函数Jm(U,V)计算公式如式(4)所示:

(4)

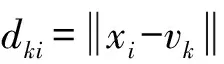
FCM聚类算法的聚类准则是令目标函数Jm(U,V)最小,聚类中心和隶属度矩阵的迭代公式如式(5)和式(6)所示:

(5)

(6)

设置迭代停止条件ε,比较第α次和第α-1次迭代得到的隶属度矩阵Uα和Uα-1,如果满足式(7),说明目标函数已达到极小值,迭代终止,否则根据式(5)和式(6)继续迭代,直到满足式(7)为止。

(7)

基于FCM聚类的交通拥堵状态识别算法的思想如下:首先确定聚类类别数为5,即将交通流数据划分为畅通、基本畅通、轻度拥堵、中度拥堵、严重拥堵5个等级;其次将训练集各个时刻的样本点xi=(xi1,xi2)作为训练样本,其中xi1和xi2分别表示历史交通量和时间占有率数据,采用FCM聚类算法对样本集进行聚类划分,得到5种交通状态对应的聚类中心,以及各个样本点分别相对于这5个聚类中心的隶属度;根据式(8)确定各个时刻交通流数据隶属度的最大值,最大隶属度值所对应的类别即为该时刻最可能的交通状态。

(8)

2.3 短时交通流参数预测算法

径向基函数(radical basis function,RBF)神经网络是一种局部逼近的三层前反馈神经网络,具有很强的非线性拟合能力。其拓扑结构见图3。

图3 RBF神经网络拓扑结构示意图

x=(x1,x2,…,xl)T、o=(o1,o2,…,oq)T、y=(y1,y2,…,yp)T分别表示网络输入、隐藏层节点输出、网络输出,ωfg表示第f个隐藏层节点到第g个输出节点的连接权值。本文选择高斯核函数为径向基函数,隐藏层节点输出of的计算公式如式(9)所示:

(9)

式中:zf表示第f个径向基函数中心,由输入样本中随机选取q个样本作为径向基函数中心,即隐藏层节点;σ表示径向基函数的标准差,即函数产生明显输出信号的区域范围,本文选取统一的标准差,计算公式如式(10)所示:

(10)

式中,dmax表示所选径向基函数中心的最大距离。

神经网络的第t个输出yt的计算公式如式(11)所示:

(11)

目标函数选用均方误差(mean squared error,MSE),计算公式如式(12)所示:

(12)

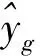
根据混沌理论提取的交通流多维信息确定神经网络的输入层和输出层节点数。首先对原始序列H={h1,h2,…,hn}进行相空间重构,将其映射到高维空间,得到多维时间序列G={g1,g2,…,gn-(γ-1)τ},其中gi的展开式如式(13)所示:

gi=(hi,hi+1,…,hi+(γ-1)τ)T

(13)

式中:γ表示相空间重构的嵌入维数;τ表示相空间重构的时延。

将最优嵌入维数和时延分别作为神经网络输入层和输出层数目可以得到较佳的预测性能[18],本文给定时延τ=1,确定最优嵌入维数γ=3。

得到短时交通流数据预测值后,构建预测样本集的特征指标矩阵,计算预测样本集中每个样本点和已得到的5个聚类中心的欧氏距离,与样本点欧式距离最短的聚类中心所对应的交通拥堵状态即为预测的该样本点的交通拥堵状态,实现短时交通拥堵状态预测。

3 结果分析

3.1 交通拥堵状态识别结果分析

基于FCM聚类算法进行交通拥堵状态识别。首先对模型设定相应的初始参数:聚类个数c=5,模糊加权指数m=2,迭代停止阈值ε=10-6。采用归一化处理后的训练集数据进行FCM聚类划分,并通过分析交通流参数特征,为每个类别赋予特定的拥堵状态。最终得到训练集数据的聚类结果,如图4所示。

以1007检测器为例,FCM训练得到的聚类中心矩阵为:

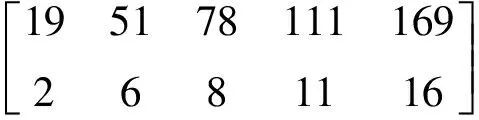
(14)

矩阵Q和矩阵O分别代表反归一化后5 min的交通量(单位:veh/5 min)和时间占有率(单位:%)。交通量和时间占有率的数值越大,交通拥堵程度越高,因此聚类中心矩阵v1、v2、v3、v4、v5分别代表畅通、基本畅通、轻度拥堵、中度拥堵、严重拥堵状态所对应的聚类中心。

FCM聚类算法是无监督学习算法,没有唯一的评价标准,根据类内高聚合、类间低耦合的原则进行算法性能评价。从图4可以看出,同一交通状态的样本点分布较为规整紧密,不同交通状态之间分界线明显,可以清晰看出各个时刻交通数据点的分布以及归属的交通状态,训练结果稳定有效。

为了进一步说明FCM聚类算法得到的聚类结果的可靠,将本文测试集数据用于K-means聚类算法,以进行对比分析。多次训练发现,K-means聚类算法每次训练得到的聚类结果不同,大致有4类,以1007检测器为例,聚类结果如图5所示。

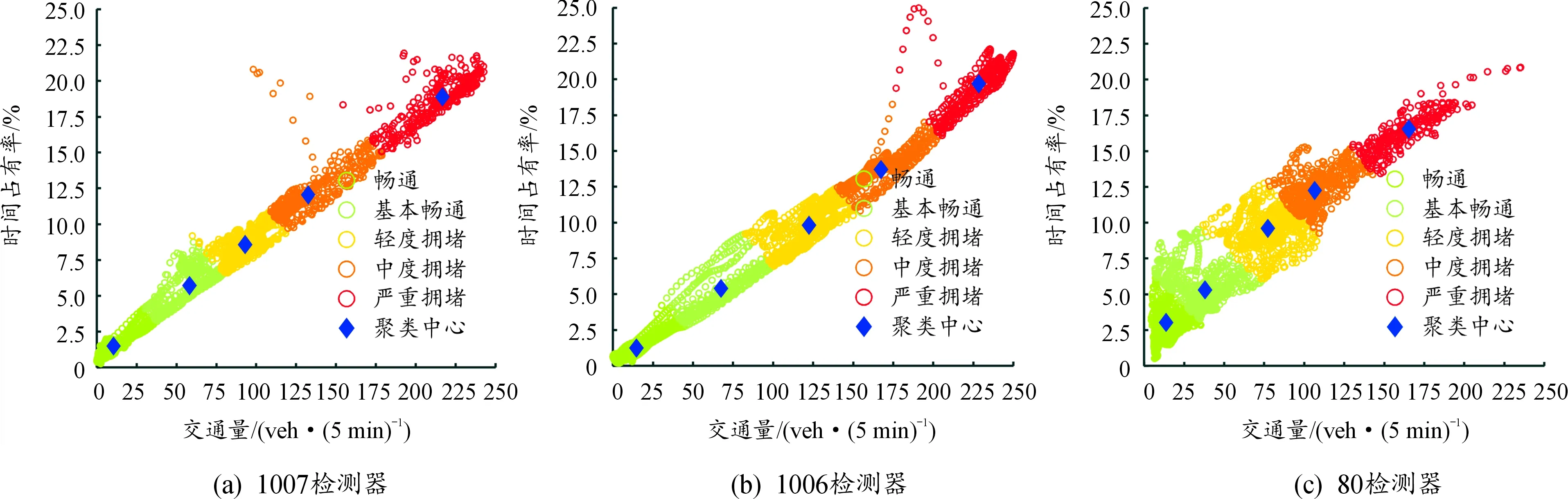
图4 FCM聚类划分的结果

图5 K-means聚类划分的不同情况的结果

图5(a)(b)表示随机选择的部分初始聚类中心远离数据集的中心点,导致没有分配到该聚类中心所在集合的数据点,聚类数目少于预期聚类数目;图5(c)表示随机选择的部分初始聚类中心为孤点,聚类结果陷入局部最优解;图5(d)表示理想的聚类结果。从上述分析可以看出,K-means算法需要反复多次试验才能得到理想聚类结果,结果不稳定,且与初始聚类中心的选取密切相关。相比较而言,FCM算法每次聚类结果相近,聚类结果稳定可靠。产生这种结果的原因是K-means算法将样本点硬性地规定为某一类,用于修正聚类中心的元素只有上次迭代得到的一部分。而FCM算法将样本点按照相关性计算隶属度,每一个聚类中心的修正都由样本中全部聚类中心参与,结果也更精确。

3.2 短时交通流参数预测分析

基于RBF神经网络算法对目标路段进行短时交通流参数预测,需要单独训练2个模型,即交通量预测模型和时间占有率预测模型。首先对模型设定相应的初始参数。通过最优嵌入维数和相应的时延确定2个RBF神经网络输入层和输出层节点数目均分别为3和1,即以目标路段在当前时刻之前15 min的实时交通流参数预测下一时段(未来5 min)的交通流参数,且每次预测1个步长。

隐藏层节点数确定的方法为:从一个神经元开始,计算输出误差,不断自动增加隐藏层神经元个数,循环多次实验,直到达到误差要求或预先设定的最大隐藏层神经元数目。确定标准差为1,目标均方误差为10-5。

将经过归一化处理的一维训练数据集(交通量和时间占有率)进行相空间重构,得到多维时间序列G={g1,g2,…,gn-(γ-1)τ}。将gi和gi+1(γ)分别作为输入向量和对应的输出向量,对RBF神经网络进行训练。采用训练好的RBF神经网络对测试集数据进行短时交通流参数预测,得到各个时段交通量和时间占有率的短时预测结果。以1007号检测器为例,反归一化后的交通量和时间占有率的短时预测结果和原始数据见图6。

从图6可以看出,RBF神经网络得到的预测输出值和实际输出值较为接近。为了分析预测性能,更清楚地看出预测值和实际值之间的误差,计算出各个时刻的预测相对误差,以1007号检测器为例,各个时段的预测残差如图7所示。

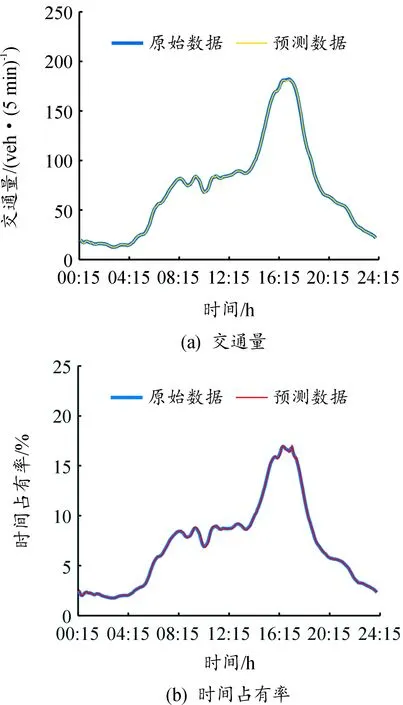
图6 交通量和时间占有率预测值和实际值

图7 交通量和时间占有率预测相对误差

交通量和时间占有率的预测结果和观测数据的均方误差的统计结果如表3所示。

从表3可以看出,3个检测器的预测结果大致接近,交通量和时间占有率预测相对误差值统计结果相接近且数值较小, 75%以上的预测值的误差均在1.2%以下,预测精度较高,说明采用RBF神经网络算法对交通量进行短时交通流预测结果精度较高。

将RBF神经网络模型的预测结果与在交通流预测方面广泛应用的BP神经网络模型、SVM模型、KNN模型的预测结果进行对比,对比结果如表4所示。

从表4可以看出,RBF神经网络的平均相对预测误差相对于其他模型较小,且75%的相对预测误差也均相对于其他模型更小,证实了RBF神经网络预测结果的可靠性,可以用于进行常发性交通拥堵路段的短时交通流预测。

3.3 短时交通拥堵状态预测分析

根据3.1节得到的不同交通拥堵状态的聚类中心, 分别计算3.2节预测得到的短时交通流参数数据中各个样本点与聚类中心的隶属度,建立各个时刻样本点对于不同交通状态类别的不确定描述。根据最大隶属度原则,判断样本所处的交通状态,结果如表5所示。

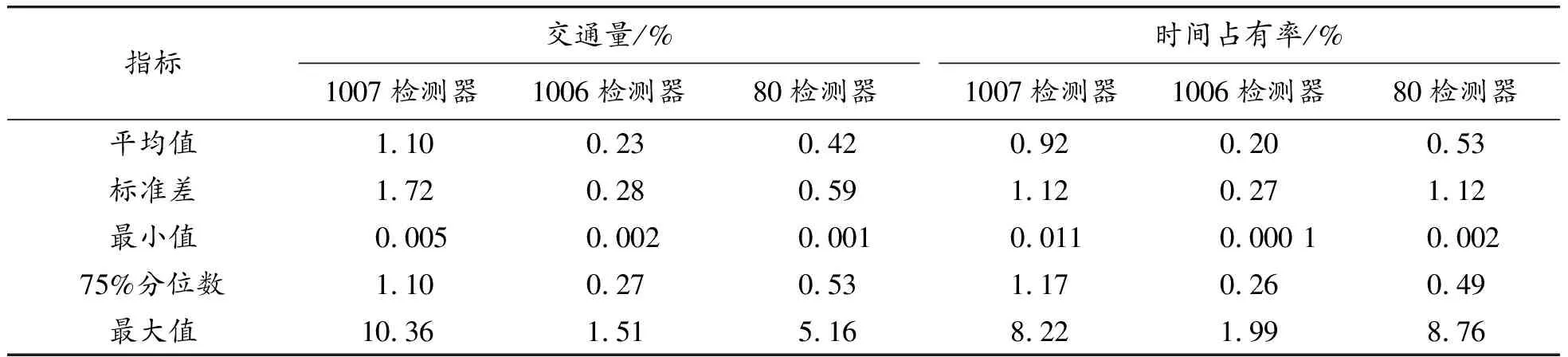
表3 交通量和时间占有率预测相对误差

表4 不同预测模型的交通量和时间占有率相对预测误差

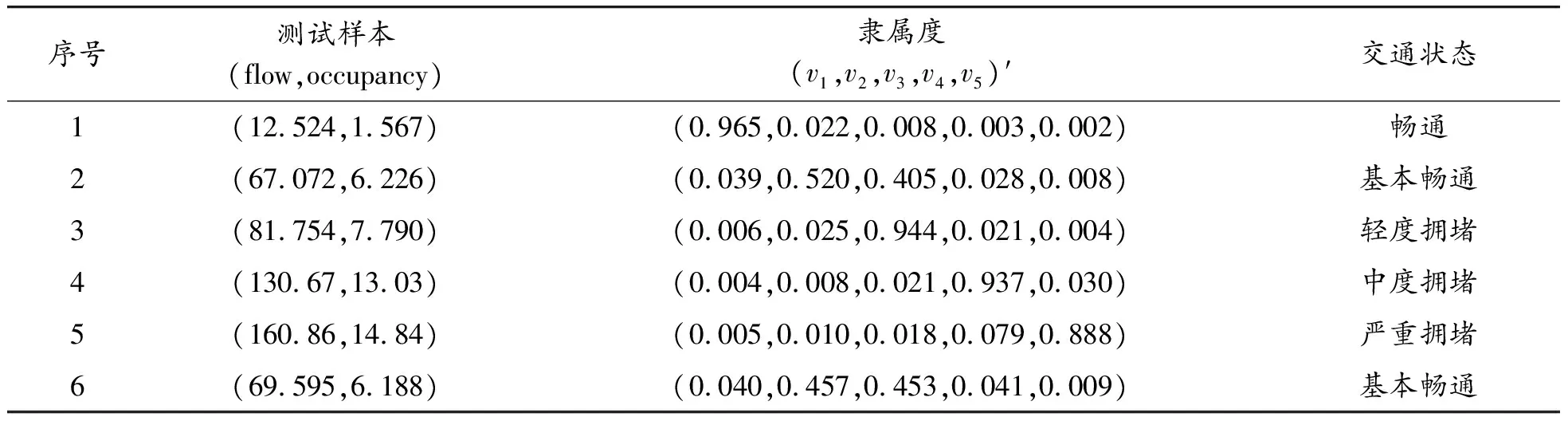
表5 部分样本交通拥堵状态预测结果

预测得到测试集各个时段的短时交通拥堵状态后,与识别的对应时刻的实际交通拥堵状态比较,以1007检测器为例,结果如图8所示。

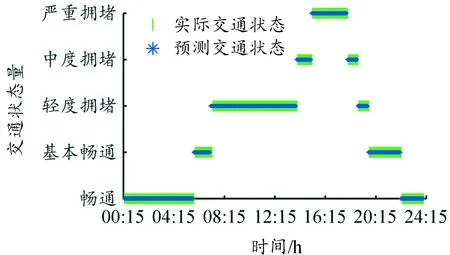
图8 识别及预测的交通状态等级示意图

图8显示交通状态等级的识别结果与预测结果基本吻合。3个检测器在00∶15—24∶00时间内285个时间间隔中分别有9、6、14次误判数据,交通拥堵识别准确率为96.8%、97.9%、95.09%,均在95%以上,预测精度较高。因此,由上述分析可以看出,在模型识别正确率方面,本文算法具有较好的优越性,可以用来进行短时交通拥堵状态预测。