由一道解析几何问题引发的思考

娄超 杨雪梅

《数学通报》2021年第12期中刊载了江苏省苏州 实验中学王弟成老师的《一类根与系数关系不对称解 析几何题解法探究与原因探析》一文，文中谈及的根 与系数的关系不对称的解析几何问题比较常见，于是 笔者对这类问题进行了深入的研究，找到了解答此类 问题的几种方法.下面结合例题进行探讨.

例题：

解：

可以看出此时方程的根与系数的关系不对称，我 们就不能直接用韦达定理建立关系式，那么该如何处 理呢？经过分析、研究，笔者总结了如下几种求解思路.

思路1：运用特殊到一般思想

特殊到一般思想是指通过特殊情形了解一般情 形，从而得出一般规律的思想.运用特殊到一般思想解 题，可以根据题意选取合适的特殊数值、特殊函数模 型、特殊位置、特殊图形，将其代入题设中建立关系 式，便可快速得出结论.再对所得结论进行验证，即可 解题.

解：

我们先根据题意取特殊点 A（-1， 3 2 ） ，B（-1，- 3 2 ） ， P（-4， 3 2 ） ，即可快速确定直线 PB 的方程，得出 M 点的 坐标；然后根据韦达定理证明 -4 - my1y2 + 3y1 y2 - y1 = - 5 2 即可.

思路2：采用代入消元法

对于含有多个变量的代数问题，我们通常可采用 代入消元法来化简代数式.先寻找变量之间的关系式， 用其中一个或两个变量表示其他变量及其关系；再将 其代入代数式中，便可消去其他变量，减少变量的个 数，使得根与系数的关系式简化.

解：

我们根据韦达定理将 y1y2 用 y1 + y2 表示出来，即 可将 x 的表达式化为只含有 y1 + y2 的式子，再通过简 单的运算即可化简根与系数的关系式.

思路3：利用求根公式

解：

利用求根公式求得一元二次方程的两根，并将其 代入代数式中进行计算，即可化简根与系数的关系式.

思路4：构造对偶式

當方程的根与系数的关系不对称时，为了化简代 数式，可以根据代数式的特征构造出对偶式，即改变 变量、符号，却不改变代数式的结构，通过加减相消， 化简根与系数的关系式.

解：

分别设 A（x1，y1） 与 B（x2，y2） ，B（x1，y1） 与 A（x2，y2） ，即 可构造出对偶式，将两式相加，便可消去其中的部分 项，通过计算即可化简根与系数的关系式.

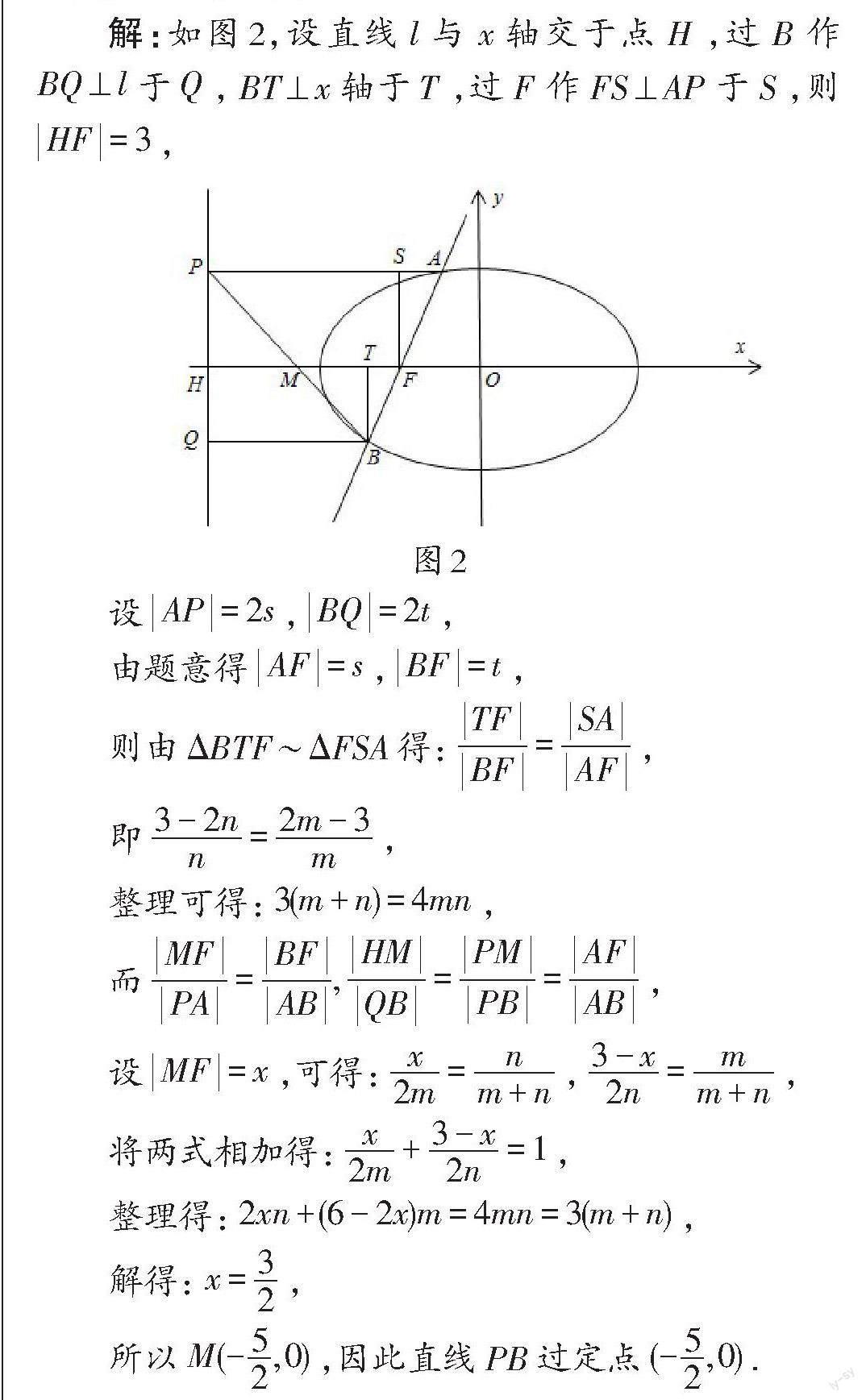
思路5.利用几何图形的性质

对于解析几何问题，我们不仅可以从曲线的方程 入手，还可以从图形入手，根据图形的特征添加辅助 线，利用三角形、圆、平行四边形、梯形的性质来建立 几何关系式，以使问题获解.

解：

对于解析几何问题，同学们要学会将数形结合起 来，通过研究图形来建立几何关系，把几何关系用数 量表示出来，即可快速解题.

总之，对于这类方程的根与系数的关系不对称的 解析几何问题，同学们可将其视为代数问题，通过消 元、代换、构造对偶式来化简代数式，也可将其视为几 何问题，通过几何关系、利用几何图形的性质来寻找 解题的思路.根与系数的关系不对称的解析几何问题 是一类非常规问题，同学们需打破思维定式，另辟蹊 径，才能破解难题.

（作者单位：山东省东营市第一中学）