一种距离多普勒平面的二维点迹凝聚方法

郑东卫 白亚莉

(1.西安电子工程研究所 西安 710100;2. 西安昆仑工业(集团)有限责任公司 西安 710043)

0 引言

原始点迹数据主要分为虚假点迹和分裂点迹两大类。不期望的物体杂波、干扰等所产生的点迹,都属于虚假点迹。在很多情况下,由于目标或系统自身的原因一个目标会分裂出多个点迹,这些由目标分裂所产生的点迹称为分裂点迹。减少虚假点迹主要通过雷达的信号处理系统完成,例如采用动目标检测、动目标显示、恒虚警检测、杂波图等处理方法。对于同一目标的雷达天线扫掠过程中,回波信号经信号处理和恒虚警检测后,点迹提取器录入两个或两个以上的目标点迹的现象,称为目标分裂[1],即检测处理后目标产生了分裂,一个目标被判断成几个目标。三坐标雷达目标分裂可分为距离分裂、多普勒分裂、方位分裂、俯仰分裂等。

距离维由于距离分辨单元一般大于采样单元,且脉压时加窗匹配滤波处理后导致主瓣展宽,使输出的目标回波信号会被量化到不止一个距离单元中,即一个目标在距离上被分裂为2个或2个以上的点迹数据。

对于动目标检测体制雷达来说,目标的点迹数据会在多个滤波器组、多个相参积累时间重复出现,所以目标会在多普勒通道上产生分裂目标。

当雷达天线波束扫过目标后,由于天线波束有一定的宽度,目标回波在俯仰维和方位维均呈现天线方向图调制特性,即目标回波会跨越多个俯仰或方位单元。

所以对于多数相控阵雷达,点迹凝聚需要在距离维,多普勒维,以及方位维、俯仰维进行进行凝聚。

本文重点介绍在距离维和多普勒维同时进行凝聚。

1 一维凝聚存在的问题

为了在FPGA,DSP或CPU中快速实现点迹凝聚,目前很多雷达凝聚都是采用“十字交叉法”,也即先对每个多普勒通道分别利用质心法进行距离维凝聚,然后对每个距离单元分别利用质心法进行多普勒维凝聚。由于目标起伏和系统测量误差等原因,经过距离维凝聚后,同一目标在相邻的多普勒通道中对应的距离单元可能存在一定的偏差,即在相邻的多普勒通道间,经过距离维凝聚得到的距离单元由于误差而无法“对齐”,因此,如果采用传统的“十字交叉法”进行凝聚,则无法将本属于同一目标的点迹凝聚在一起,从而出现一个目标在凝聚后分裂成多个目标的情况。如图1所示。

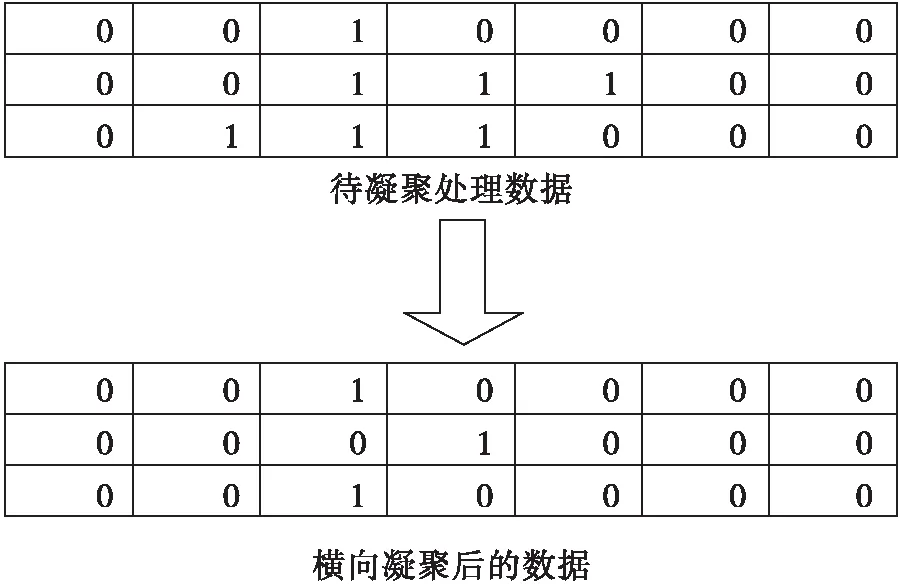
图1 横向凝聚示例

图1中每一列数据中1代表不同距离单元检测到的点迹,每一行中1代表不同多普勒通道检测到的点迹。将待凝聚处理数据先进行同一多普勒通道距离维凝聚后得到横向凝聚后的数据。凝聚完后不同多普勒通道距离维数据没有对齐,会出现目标分裂。

2 二维凝聚算法

目前凝聚算法有很多种,文献[2]中提出的先在距离维凝聚,然后在俯仰维,接着再在方位维凝聚,采用的串行处理方式。文献[3]使用图像分割经典算法——泛洪填充算法检测目标的连通区域。考虑到在目标距离维上的凝聚结果做了取整处理和目标在各个距离—俯仰维上存在随机扰动现象,采用八邻域泛洪算法。还有文献[4]杨刚等人提出的父子节点凝聚方法等。

本文提出了一种距离多普勒平面的二维点迹凝聚方法,该方法通过先对目标检测后点按一定顺序排列,接着在相同多普勒通道进行距离维归并,然后再进行多普勒维归并,接着将二维归并完的目标点根据目标判决条件剔除虚假点,最后将剩余的目标点按一定准则凝聚形成最终结果。

二维距离多普勒点迹凝聚包含五个步骤。

1)步骤一:

先对经过恒虚警和杂波图门限检测得到的点迹按多普勒通道号从小到大进行排列,然后在同一个多普勒通道号内再按距离单元号从小到大排列,得到有序的点迹数组A[N0],其中N0为检测出待凝聚目标个数。

2)步骤二:

对每一个多普勒通道内得所有距离单元找距离单元相邻的点,将相邻的点整理归并到一起,将距离相邻目标点算一个整体点,这样所有多普勒通道数据整理后,目标划分为N1个整体,N1≤N0,并且与目标大小占据几个距离单元相关。对每个整体内相邻目标点内目标个数记为M0,M0≤N0。这时目标点整理为二维数组B[N1][M0]。

点迹在距离维上归并主要是要确定目标起始和目标终止的距离单元。具体方法如下: 将距离单元上第一个出现的目标判定为目标起始,记为Rstart,当距离单元上连续出现目标且距离单元间隔小于指定的距离波门宽度a,则将最后距离单元上的目标判定为目标终止,记为Rend,对于满足P≤Rend-Rstart≤Q的序列判定为目标。其中,a、P、Q参数的取值由雷达距离分辨率和目标散射截面积特性决定,具体计算可参考式H=L/l式中,H为目标反射截面积所占用的距离单元个数,L为目标反射截面积的距离长度,l是雷达距离分辨率。

3)步骤三:

对二维数组B[N1][M0]内的N1行M0列的每个目标点与数组内的不同行每一列目标点进行多普勒比较,找出距离相邻或相同,多普勒相邻的目标点,将这些点整理归并到一起,算一个整体,这样目标划分为N2个整体点,每个整体点内目标个数记为M1,N2≤N1,M0≤M1≤N0。这时目标点整理为二维数组C[N2][M1]。每一行内M1个目标满足距离单元相邻,多普勒相同或相邻的条件。N2行代表整体点目标的个数。

4)步骤四:

将数组C[N2][M1]中每一行中M1个目标可根据一维凝聚算法中将不满足条件的目标剔除,变为数组D[N2][M2],N2≤N1,M1≤M2≤N0。

M1个目标剔除的原则为:经过步骤二后延续的距离单元小于等于目标的脉冲宽度。这时要判断距离单元相邻的原始点迹数据的幅度差值是否大于门限值。门限的值取决于脉冲宽度和脉内取样点。当幅度差值大于门限值时,可剔除掉幅度小得目标;当幅度差值小于门限值时,这批原始点迹数据属于同一个目标,保留这些点迹信息。邻近点迹数据的多普勒差值也应当小于某一门限值,门限值的选取由雷达脉冲积累的FIR滤波器或FFT精度来确定。

5)步骤五:

将数组D[N2][M2]的中每一行的M2个目标凝聚为一个点,数组变为E[N2]个目标点。每个目标点可采用以下三种方法进行凝聚:一是选取幅度最大的点迹的距离单元、多普勒通道、幅度值作为凝聚目标的幅度、距离、多普勒信息;二是利用式(1)、式(2)、式(3)求重心的方式,求取目标的幅度ampnew,距离disnew,多普勒信息duoplnew;三是采用二次曲线拟合[5]的方法式(4)求得目标的距离,多普勒信息等。

(1)

(2)

(3)

其中M2为当前目标在当前行的点迹个数;amp(m)为第m个点迹的幅度;dis(m)为第m个点迹的距离;duopl(m)为第m个点迹的多普勒信息。

采用二次曲线拟合的方式来求解内插距离。方法是:根据连续三个距离单元上相同频率通道的幅度值,假设中间距离单元的幅度大于两侧距离单元的幅度,拟合一条经过这三个点的抛物线,计算出抛物线最大值所对应的X轴坐标值,此坐标即为中间距离单元的内插距离。如图2所示,以距离单元为X轴,以幅度为Y轴,在相邻的距离单元x1,x2,x3上,相同滤波器通道的幅度值分别为y1、y2、y3,距离单元x2处的内插距离公式为

(4)

图2 距离内插示意图

距离多普勒平面的二维凝聚方法流程见图3所示。

3 实例说明

现结合实例对本方法做进一步描述。举例说明,现有一个二维检测平面,距离单元个数为8,多普勒通道个数为6,检测出的目标个数N0=12个,每个目标点距离,多普勒,幅度大小见图4中阴影部分所示。

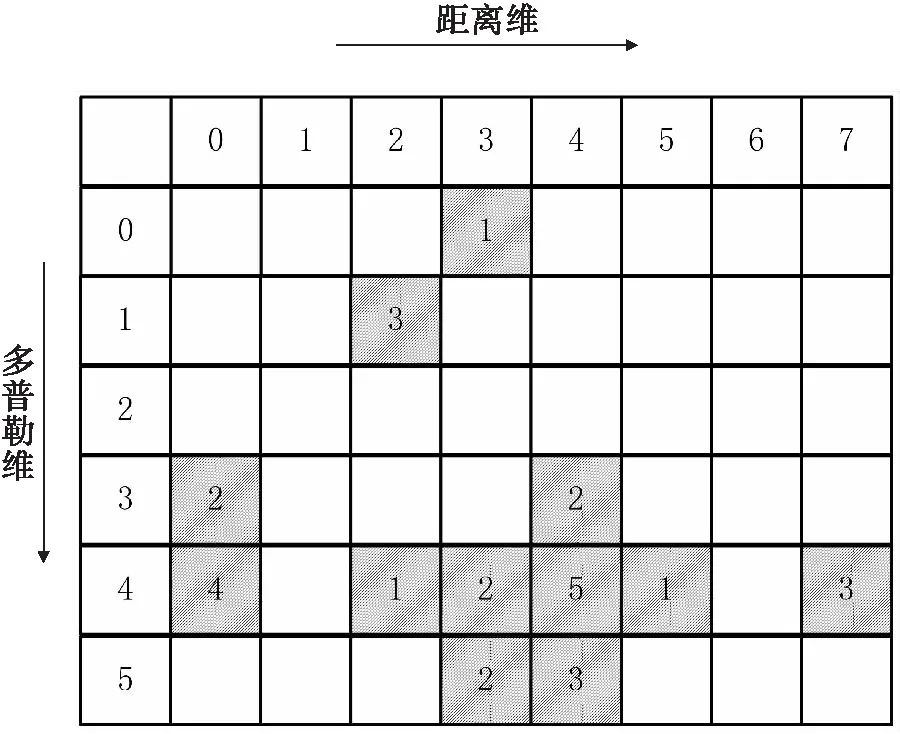
图4 点迹凝聚前距离多普勒平面示意图

步骤一:先将目标点整理为数组A[12],数组中每个目标用多普勒和距离区分。数组内部按多普勒从小到大,每一个多普勒中距离单元按从小到大排列,得到数组A[12]。

A[12]=[a03,a12,a30,a34,a40,a42,a43,a44,a45,a47,a53,a54]。数组中每个元素下标分别表示多普勒通道号和距离单元号。

步骤二:将每一个多普勒通道数据归并完形成数组B[8][4]。

B[8][4]=[a03, 0, 0, 0;

a12, 0, 0, 0;

a30, 0, 0, 0;

a34, 0, 0, 0;

a40, 0, 0, 0;

a42,a43,a44,a45;

a47, 0, 0, 0;

a53,a54, 0, 0]。

步骤三:将不同行多普勒通道的目标找距离单元相邻或相同的点,归并为数组C[4][7]。

C[4][7]=[a03,a12, 0, 0, 0, 0, 0;

a30,a40, 0, 0, 0, 0, 0;

a34,a42,a43,a44,a45,a53,a54;

a47, 0, 0, 0, 0, 0, 0]。

步骤四:可根据一维凝聚算法中将不满足条件距离凝聚和多普勒凝聚的目标剔除,比如可以剔除掉幅度为1的目标,剔除完为数组D[4][5]。

D[4][5]= [a12, 0, 0, 0, 0;

a30,a40, 0, 0, 0;

a34,a43,a44,a53,a54;

a47, 0, 0, 0, 0]。

步骤五:将每一行的目标凝聚为一个点,采用三种方法之一来凝聚目标,凝聚为数组E[4]。

E[4]=[a12,a40,a44,a47]。

最终凝聚完目标点示意图如图5所示。

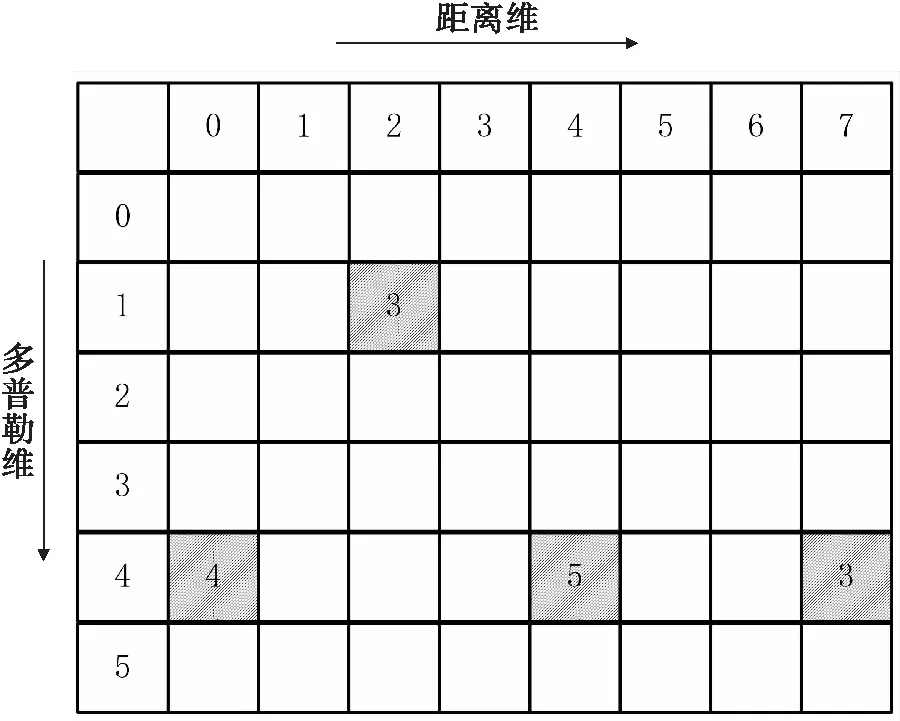
图5 点迹凝聚后距离多普勒平面示意图

由此可见,经过五个步骤的处理,二维距离多普勒平面的目标点凝聚为最终目标点,没有出现目标分裂。

通过Matlab仿真分析该算法。一距离单元为64,多普勒通道为32点的20个目标点的凝聚前后距离多普勒平面对比效果如图6所示。凝聚完后为4个目标点。

通过仿真对比凝聚前后目标点信息,可以看出经过此算法,目标点得到了很好的凝聚。

4 结束语

本文提出了一种距离多普勒平面的二维点迹凝聚方法,该方法通过先对目标检测后点按一定顺序排列,接着在相同多普勒通道进行距离维归并,然后再进行多普勒维归并,接着将二维归并完的目标点根据目标判决条件剔除虚假点,最后将剩余的目标点按一定准则凝聚形成最终结果。通过二维归并凝聚可以避免目标分裂现象。该方法已在现实产品中得到了应用,证明了其在工程上的实用性。

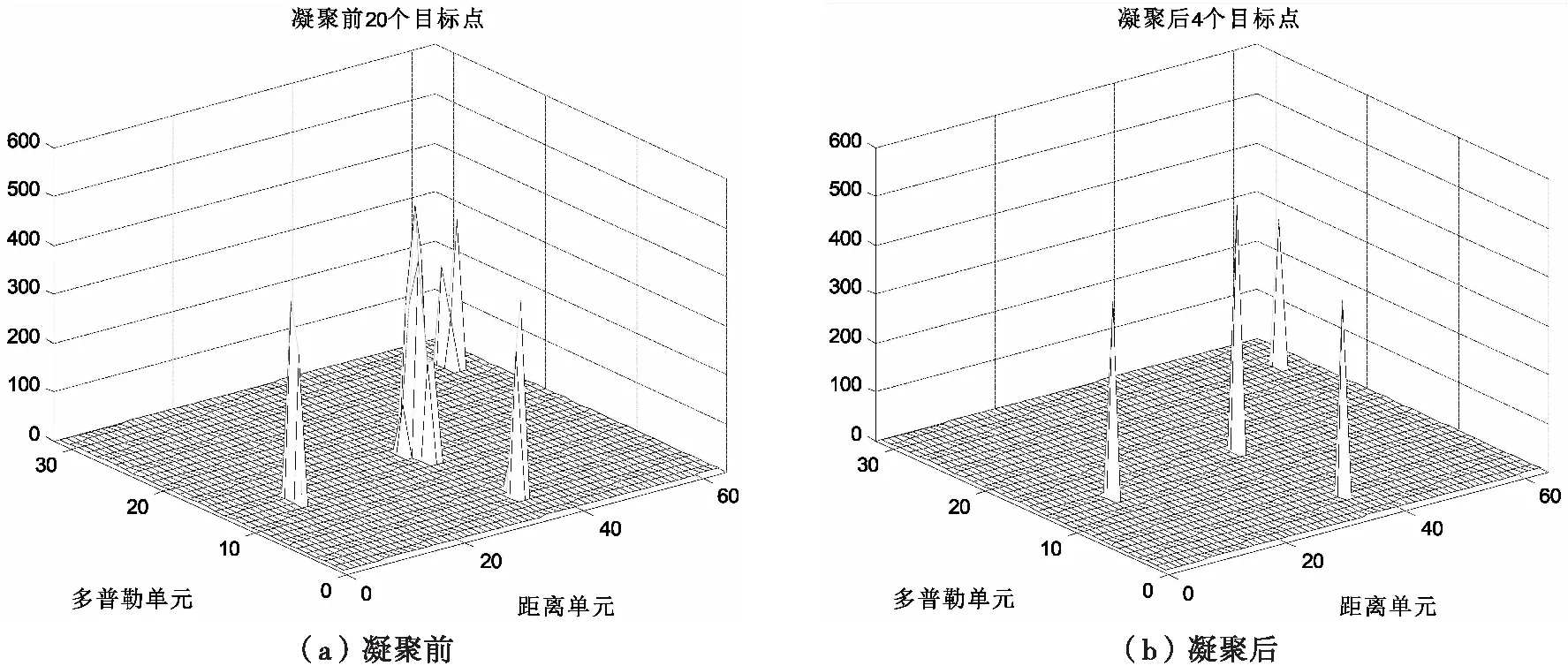
图6 目标点凝聚前后距离多普勒平面对比