球直坐标变换非对称误差分析

李慧敏 马 可 范学祯

(西安电子工程研究所 西安 710100)

0 引言

对于常见的雷达、光电等主动探测设备,信号收发一般放置在一起,称作单站测量,单个接收站可独自获取目标的距离、角度等信息。对于收发分置的探测设备来说,目标参数的获取方式只要不依赖于多个接收站之间的配合,也可称作单站测量设备。

对于单站测量设备来说,其原始测量值在球坐标系下获取,各测量值的误差一般是互相独立的,而滤波、外推等算法则在直角坐标系下进行,由于球坐标与直角坐标之间的非线性映射关系[1-2],导致测量误差互相耦合,空间分布产生畸变。

滤波的前提是随机变量的期望值等于目标真实位置[3-5],但若期望偏离真实值,则滤波值必然偏离目标真实位置。对于比较常见的直线运动轨迹,如果测量误差在直线两侧的分布不对称,将导致目标运动轨迹滤波值产生单侧偏移,产生系统偏差。这种系统偏差对于一些需要外推遭遇点的应用场景来说[1,6],误差将进一步放大,因此必须引起重视。

本文从球坐标系与直角坐标系的坐标变换出发,对直角坐标系下误差分布的非对称性进行了分析计算。

1 球坐标系与直角坐标系的坐标变换

以两坐标雷达为例,球坐标系到直角坐标系的坐标转换公式见式(1)所示。

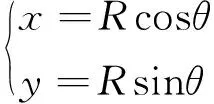
(1)

其中R、θ为球坐标系下的原始测量值,分别代表目标距离和角度,x、y为直角坐标系下的坐标值。坐标逆变换公式为

(2)

两种坐标系之间的非线性映射关系如图1所示。

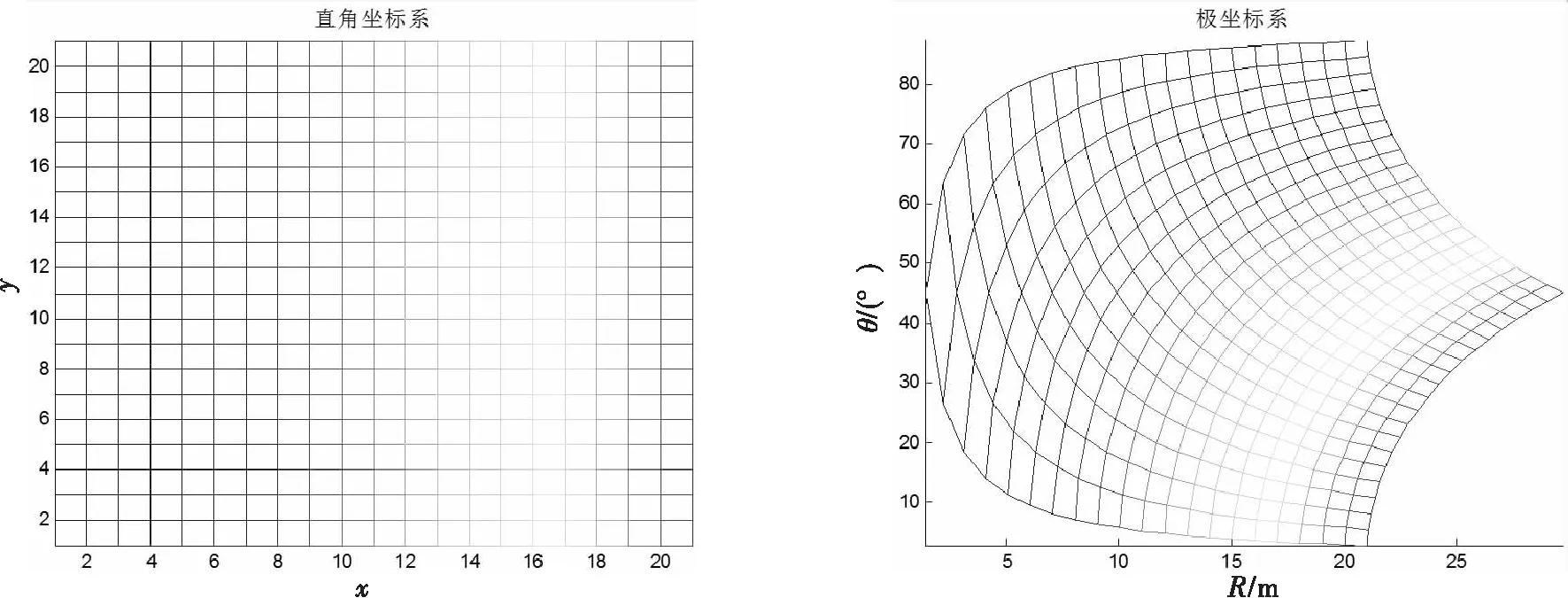
图1 直角坐标系与球坐标系之间的非线性映射

我们描述物体的运动轨迹是“直线”的,一般均默认其处于直角坐标系。直线轨迹转换到球坐标系下后,其距离-角度曲线一般都不再是直线。

直线轨迹可分为两种:截距为0和截距不为0。

1)截距为0时,x、y的关系式为y=cx,根据坐标逆变换公式可推导得球坐标系下的关系式为θ=tan-1c,可知此时角度θ为恒定值,距离-角度关系体现为直线。

2)截距不等于0时,x、y的关系式为y=cx+d,且d≠0,将式(1)带入可得Rsinθ=cRcosθ+d,两边同时对R求导数,整理后可得

(3)

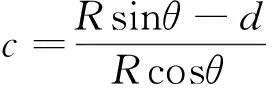
(4)

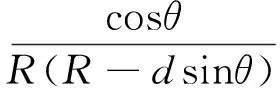
图2 直角坐标系与球坐标关系示意图

2 球坐标系下的误差分布

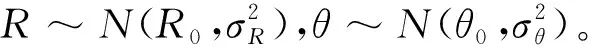
(3)

在球坐标系下,该函数关于点(R0,θ0)呈对称分布,如图3所示。

图3中的圆环为概率分布等高线。在(R,θ)二维平面上,任意一条通过点(R0,θ0)的直线θ=a·R+b,均可将p(R,θ)等分,即满足

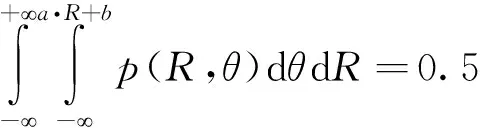
(6)

图3 二维联合概率密度函数

根据第2节的结论:截距d=0时,θ=tan-1c。此时在(R,θ)坐标系下表现为一条直线,如图4所示。

图4 概率密度函数关于θ=tan-1c对称分布

因此θ=tan-1c将概率密度函数等分为两部分,误差在直线两侧的分布概率是相等的。

根据第2节的结论:截距d≠0时,在(R,θ)坐标系下,R和θ的关系表现为一条经过点(R0,θ0)的单调曲线,假定其函数表达式记为θ=g(R)。若c、d均大于0,曲线形状如下图所示。

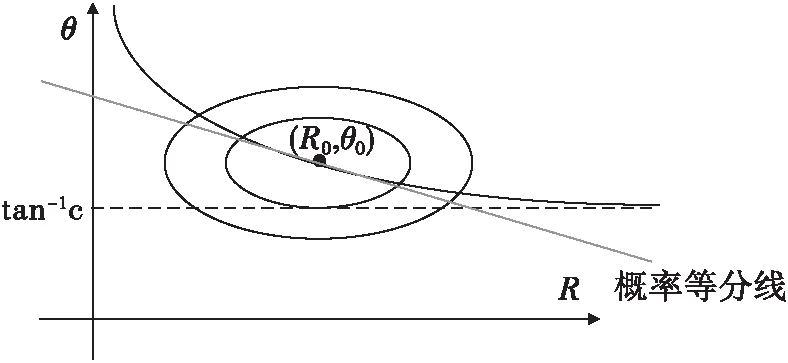
图5 概率密度函数关于θ=g(R)不对称分布

由于θ=g(R)是单调的,因此必然可以找到一条直线,在(R0,θ0)处与θ=g(R)相切。由此可得出以下结论:

1)对于曲线θ=g(R)上的任意一点(Ri,θi),其切线将(Ri,θi)处的分布概率等分为两部分。

2)对于曲线θ=g(R)上的任意一点(Ri,θi),其分布概率在曲线θ=g(R)两侧的分布概率不相等。

3)随着R的增大,曲线θ=g(R)在点(Ri,θi)处的斜率越接近于0,从而和其切线越来越靠近,因此曲线两侧的分布概率逐渐趋近相等。

由此可知,在直角坐标系下进行滤波时,目标在真实轨迹两侧的分布概率是不相等的,因此导致期望偏向真实轨迹的一侧,引起系统误差。当目标距离较近,且航路截径和目标距离相当时,其影响将比较明显;目标距离越远,该误差逐渐减小,其影响可忽略。

3 仿真计算

假定在直角坐标系下有一条直线轨迹,其坐标值x,y满足关系y=0.1x+500,x的取值范围为[100,500]。设定测距误差σR=5m,测角误差σθ=1°。

通过蒙特卡洛仿真,模拟某一特定测量点的误差散布。例如,直角坐标系下,某一点处的散布误差“点云”如图6所示。

图6 直角坐标系下的直线航迹与误差分布

其中实线为目标的直线轨迹,“点云”为轨迹上某点处的测量值散布误差。对应的球坐标系下的散布误差为图7所示。

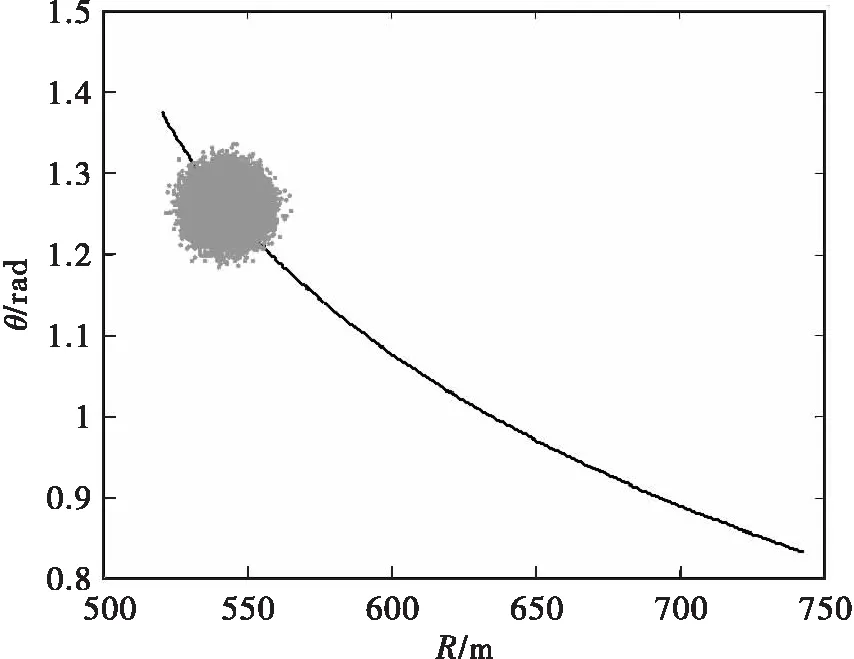
图7 球坐标系下直线航迹与误差分布

统计点云处于轨迹上方(参考纵轴正向)的点的个数,可以反映出误差的单边分布概率。对于图6中的情况,轨迹上方的单边分布概率约为49.6%,沿轨迹上各点依次通过蒙特卡洛仿真手段,分析单边分布概率,仿真结果如图8所示。

图8 单边分布概率的最小二乘拟合

图8中,细实线为通过蒙特卡洛仿真得出的单边分布概率。对仿真概率进行最小二乘拟合,近似得出实际的单边分布概率,如图8中粗实线所示。

可见,对于直线轨迹上的各点,实际的单边分布概率始终小于0.5,说明在设定的仿真条件下,轨迹上方的单边分布概率始终小于轨迹下方的单边分布概率,由于概率分布不对称,属于“偏心”分布,将导致期望值偏向轨道下方一侧。根据图8的仿真结果,可得出轨迹上每一点处目标的位置期望值,从而得到预测的目标轨迹。实际轨迹与预测轨迹对比如图9所示。

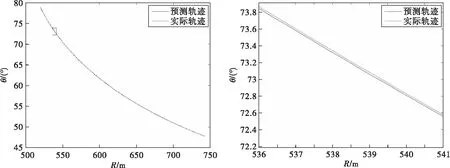
图9 直角坐标系下的实际轨迹与预测轨迹

预测轨迹和实际轨迹的差别较小,二者几乎重叠在一起,将图9左图黑色框线内部放大,如右图所示。可见由于误差的非对称分布,预测轨迹始终处于实际轨迹下方。预测轨迹偏离实际轨迹的差值变化趋势如图10所示。

图10 直角坐标系下预测轨迹与实际轨迹的偏差

目标距离越近,二者的角度系统偏差越大,最大接近0.03°,目标距离越远,偏差越小。对于远程单站测量设备来说,误差的非对称分布导致的角度系统偏差一般很小,因此在试验数据中一般无法觉察到它的存在。对于近距探测设备来说,该误差随着目标距离的减小而迅速增大,需要予以考虑。

4 结束语

球坐标系下获取的原始数据,通过坐标变换到直角坐标系下进行处理时,误差分布不再对称,导致滤波的期望值为有偏估计,引起滤波系统误差。以直线航路为例进行了仿真,结果表明该误差随距离的减小而增大,因此对远程探测设备影响较小,对近距探测设备影响较大。

对于曲线航路来说,可分段等效为直线航路,因此其误差分布在局部也是非对称的,同样,其非对称性在近距更为明显。