基于粒子群算法和控制参数化的多无人机编队重构控制方法

张 江 伟

(四川大学电气工程学院 四川 成都 610065)

0 引 言

由于无人机具有成本低、降低人员伤亡和易于操作等特点[1],近年来受到越来越多的关注,无论是在军事领域还是民用领域都有其广泛的用途。在军事领域,无人机可以用来进行战前的监视、侦察、预警和干扰敌方通信系统等任务;在民用领域,可用于地质勘探、农药喷洒和观测天气等任务[2-3]。但是对于一些特定的任务和复杂的环境,单个无人机可能无法胜任[4]。因此多无人机编队协同飞行引起了学者们广泛的研究兴趣。相比单无人机,多无人机编队有更高的生存率、更大的执行任务效率、更好的适应环境能力和更少的时间消耗[5]。但是,当环境变化或者任务改变时,就需要变换队形,即编队重构,所以研究一种安全有效的编队重构最优控制方法是很重要的[6-7]。

多无人机编队重构问题,可以被描述为给定一组有初始位置的无人机、期望的位置和一系列约束,找到每个无人机的最优控制输入使得多无人机从初始位置到达期望位置,并且满足所有约束[8]。目前国内外对于多无人机编队重构问题已经有了很多研究成果。文献[9]首先提出了编队重构的问题。文献[10]提出了一种结合控制参数化与时间离散化(CPTD)和遗传算法(GA)的混合算法,并通过改进遗传算子来寻优,有效地解决了编队重构最优时间控制问题,但是这种混合算法只表明了在二维空间的有效性。文献[11]把多无人战斗机编队重构看作一个复杂的全局最优控制问题,提出了一种变异策略改进粒子群算法的方法。文献[12]对多无人机编队重构介绍了一种离散的控制器,该控制器结合了CPTD方法和鸽启发式(PIO)最优方法,目的是为无人机找到最优的控制输入。文献[13]采用了混合粒子群算法和遗传算法相结合的方法,利用了粒子群算法和遗传算法的优势实现了对多无人机编队重构过程中参数最优问题的求解。文献[14]分析了无人机编队重构任务耦合、避免碰撞和动态拓扑的特点,提出基于模型预测控制方法对编队重构这一受约束优化问题进行求解。文献[15]基于差分进化(Differential Evolution,DE)算法,提出了一种新颖的滚动时域控制(Receding Horizon Control,RHC)的控制方法,通过在一系列滚动时域上将无人机编队重构全局最优控制问题转化为多个局部在线最优问题。文献[16]对无人机编队重构防碰撞进行了分析,采用一种分布式模型预测控制(Distributed Model Predictive Control,DMPC)算法,将编队重构问题转化为在线滚动优化问题,又采用了改进的微分进化方法对结合碰撞约束建立的重构代价函数进行求解。文献[17]提出了一种分布式鲁棒反馈控制方法用于编队和重构控制。文献[18]设计了一种反推PID(backstepping PID)控制器,对编队重组问题中的非线性和耦合性有很好的保证。文献[19]提出了一种快速搜索随机树的方法来解决无人机编队重构问题,采用多余节点去除和过度航迹修正等方法提高了规划航迹的可跟踪性。

目前现有解决多无人机编队重构问题的方法或多或少有些不足。本文以多无人机编队重构问题为研究对象,基于领航-跟随策略提出一种改进粒子群算法和控制参数化的方法。首先在三维空间建立了无人机的动力学模型,同时考虑了编队重构的终端状态约束、无人机之间的防碰撞约束、通信距离约束、控制输入约束,并将完成编队重构的时间作为优化目标。本文方法主要是为了获得更好的控制输入,更加精确地满足编队重构后的队形,其中改进的粒子群算法是用来得到一个较好的控制输入,此时重构后的队形与期望队形有点差距,之后利用控制参数化方法把改进粒子群算法得到的控制输入作为初始控制输入,此时能得到一个更优的控制输入,重构后的队形与期望一致。

1 问题提出

1.1 无人机动力学模型

假设在编队中有N架无人机,并且无人机在无侧滑的情况下飞行,发动机推力沿飞行速度方向,三维质点动力学模型下的无人机运动方程为:

式中:i=1,2,…,N;xi、yi、zi表示无人机的位置坐标;vi为无人机的飞行速度;γi、χi为无人机的俯仰角和航向角;g为重力加速度;Ti、ni、φi分别表示无人机的推力、负载因数和滚转角;Wi、Di为无人机的重力和阻力。

对于任意一架无人机假设它的状态变量为xi(t)=[vi(t),γi(t),χi(t),xi(t),yi(t),zi(t)],控制变量为ui(t)=[Ti(t),ni(t),φi(t)],用状态空间模型可表示为:

xi=x0

(3)

N架编队重构的无人机,假设x=[x1,x2,…,xN],u=[u1,u2,…,uN],f=[f1,f2,…,fN]。

1.2 无人机编队重构目标函数和梯度

假设无人机编队重构的初始时间为t0=0,终端时间t=T,T不是一个给定的值而是需要优化的参数。所以对给定的式(2)和式(3),本文考虑了一个最优时间编队重构控制问题。目标函数可以表示为:

控制输入u(t)和终端时间T有如下约束:

umin≤u(t)≤umax∀t∈[0,T],T>0

(6)

自由终端约束为:

[xi(T)-xl(T)-xi,m]2+[yi(T)-yl(T)-

yi,m]2+[zi(T)-zl(T)-zi,m]2=0

∀i≠mi∈{1,2,…,N}

(7)

式中:m表示选取第m架无人机作为领航机(中心飞机),m∈{1,2,…,N};[xi,m,yi,m,zi,m]为终端时刻T第i架无人机相对于中心无人机的期望坐标;自由终端约束是为了保证达到期望的重构队形。

定义任意两个无人机之间的距离为:

di,j(xi(t),xj(t))=

∀i≠ji,j∈{1,2,…,N}

(8)

为了防止编队中的无人机发生碰撞,任意两架无人机之间的距离必须大于安全防撞距离Dsafe,即:

di,j(xi(t),xj(t))≥Dsafe

∀t∈[0,T],∀i≠ji,j∈{1,2,…,N}

(9)

为了能实现无人机之间的实时通信,任意两架无人机之间的距离必须小于通信保障距离Dcomm,即:

di,j(xi(t),xj(t))≤Dcomm

∀t∈[0,T],∀i≠ji,j∈{1,2,…,N}

(10)

由上所述,多无人机编队重构最优时间控制问题的数学模型可以描述为:在式(2)和式(3)下,满足式(6)、式(7)、式(9)和式(10),寻找一个连续的控制输入u(t)和终端时间T使得式(5)成立。可将编队重构最优时间控制问题表示成如下数学问题:

2 编队重构最优时间控制问题的求解

这一节将介绍基于改进粒子群算法和控制参数化方法求解多无人机编队重构最优时间控制问题。首先对粒子群算法做出改进,通过改进后的粒子群算法找到一个较好的编队重构控制输入,然后将其作为控制参数化方法的初始控制输入。下面分别详细地介绍控制参数化方法、改进粒子群算法。

2.1 控制参数化方法

(1) Time Scaling方法。由于终端时间T是未知的,为了简化问题,在这里采用了一种Time Scaling方法将时域从[0,T]变换到了[0,1]。变换方法如下:

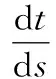
(12)

所以状态空间模型可变换到如下:

(2) 控制参数化。在时域[0,1]上,将控制变量等分为p段,控制输入函数ui,j(s)(表示ui(s)的第j个输入,j=1,2,3)可以近似为一个分段常量函数:

式中:sk=k/p,k=0,1,…,p。并且:

控制参数化的过程可由图1表示。

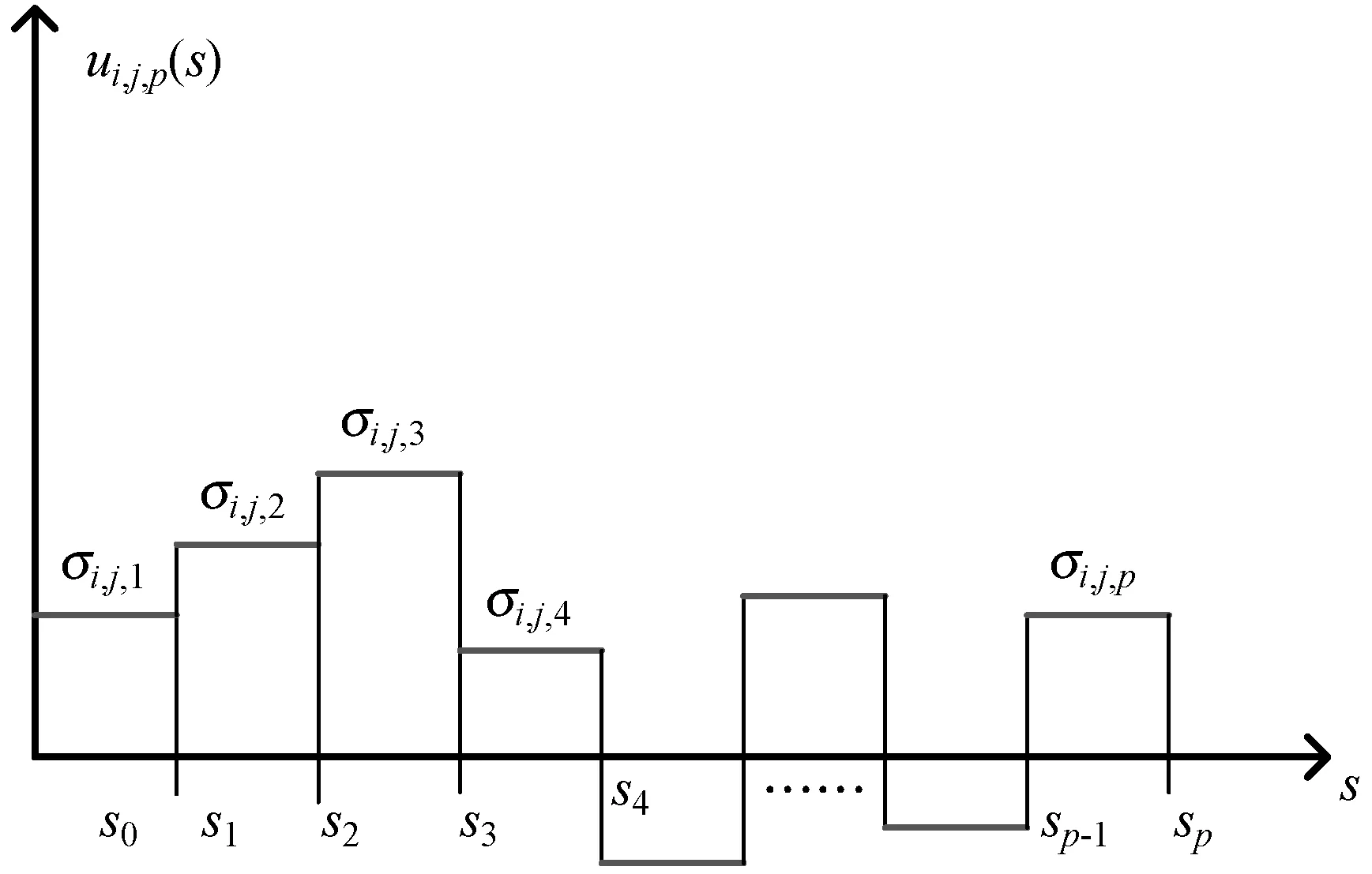
图1 控制参数化

(3) 连续状态不等式约束的转化。在编队重组中的连续状态不等式约束,由于它们包含无穷多个约束条件,所以很难处理。采用一种约束专录结合局部光滑技术可以很好地处理这些约束[19-20]。首先,可以将连续状态不等式约束等价为:

(16)

连续状态不等式约束li(x(s))有同样的等价形式,这里用gi(x(s))为例。然而,式中的min{gi(x(s)),0}是一个不光滑的函数,因此不可微,所以对于每一个连续状态不等式约束都用光滑函数Li,ε(gi(x(s)))来近似,即:

(17)

式中:ε>0是一个可调常数。设:

(18)

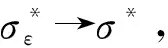
经过上面的处理约束虽然可微了,但是对于式(18)中的约束规范(constraint qualifications)不能满足,因此引入下面的近似:

gi,ε,η(x(s))=-η+gi,ε(x(s))≤0

(19)

式中:η>0。

问题中的约束都转化成了标准的形式,将转化后的问题记为Pε,η,现在给出一种基于梯度的算法来解Pε,η。

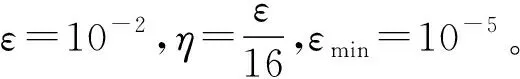
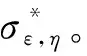
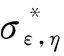
第三步:若第二步满足跳转至第五步,否则转至第四步。

第四步:设η=η/2,转至第一步。

第五步:设ε=ε/10,η=η/10,转至第一步。

当ε≤εmin时,算法终止。

下面给出目标函数和约束的梯度计算公式。

定理1目标函数梯度公式:

式中:λ0是下列协态方程的解。

λ0(1)=0

(23)

定理2重构队形终端等式约束梯度公式:

式中:λi是下列协态方程的解。

定理3目标函数梯度公式:

(29)

式中:λi是下列协态方程的解。

(30)

上述定理的证明类似文献[20]中的定理5.2.1,在这里略去了定理的证明。综合而言,编队重构问题转化为了一个最优参数选择问题,并且还是一个非线性规划问题,因此根据定理1、定理2和定理3可以采用如序列二次规划(SQP)逼近的方法来解。

2.2 改进粒子群算法

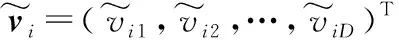
(32)

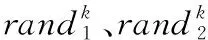
粒子通过不断地更新位置和速度以及反复迭代,直到满足求解要求或者达到最大迭代次数。

(2) 改进粒子群算法。在粒子群算法中,惯性权重系数w对求解性能有很大影响,w取值过大时,算法的全局搜索能力比较强,可以有效跳出局部解;w取值过小时,局部搜索能力较强,算法的求解精度较高,易于陷入局部最优。经典粒子群算法惯性权重是一个常值,无法满足前期全局搜索和后期的局部搜索的动态要求[21]。因此,本文采用了一种惯性权重可变化的改进粒子群算法。

(34)

式中:wmax、wmin分别为惯性权重的最大值和最小值;kmax为最大迭代次数;λ1、λ2分别为算法前期后期所占的比例,0≤λ1<λ2≤1。

在用粒子群算法求解编队重构最优时间控制问题时,采用的是罚函数法来处理约束。

2.3 改进粒子群算法和控制参数化求解过程

通过上面的描述,基于粒子群算法和控制参数化方法的多无人机编队重构问题可以分为两个阶段:改进粒子群算法求解阶段和控制参数化方法求解阶段。图2给出了求解流程。

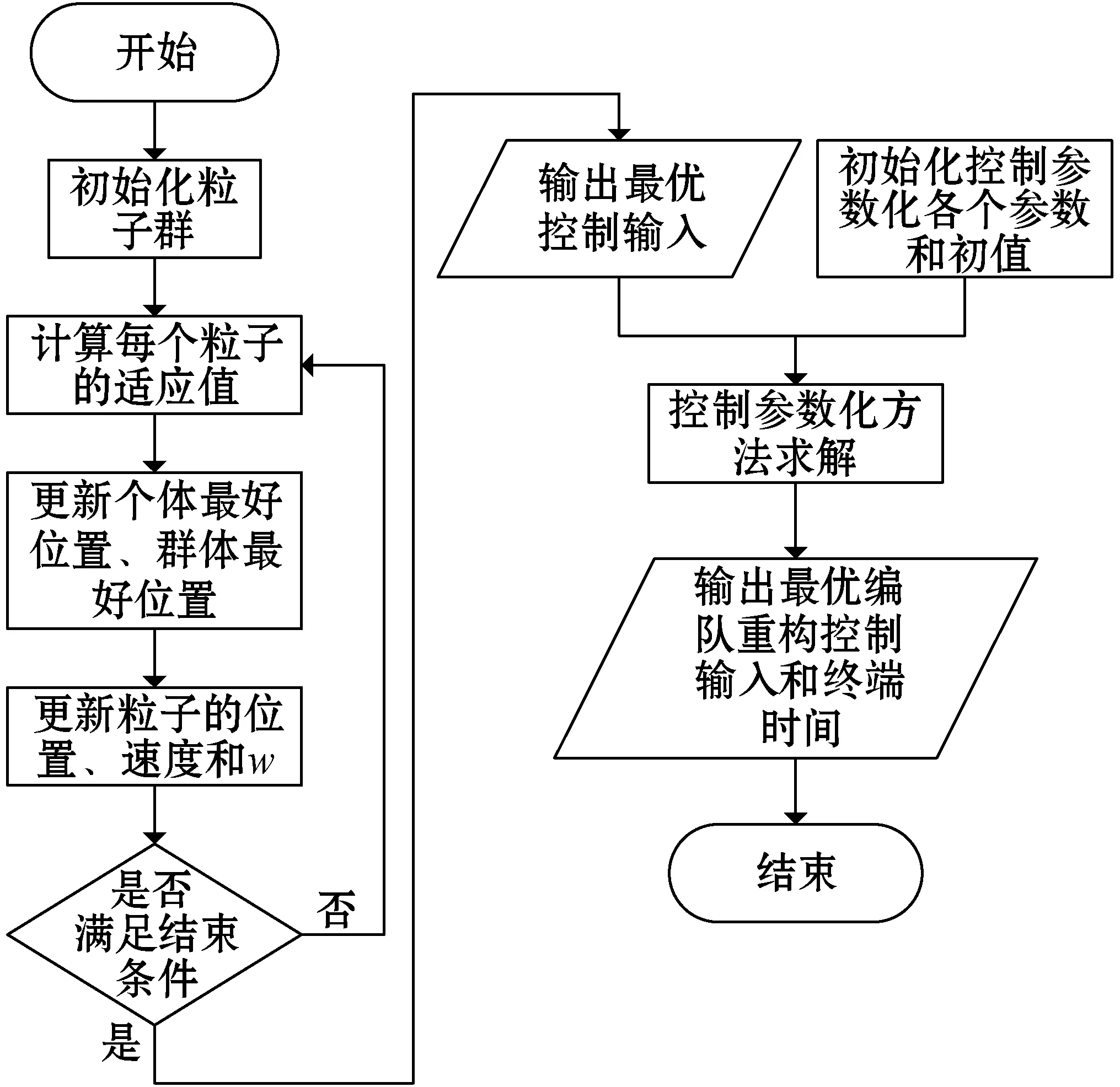
图2 求解算法流程

上面的求解过程中,改进粒子群算法求解阶段是为了给控制参数化方法求解阶段提供一个好的起始点。因为改进粒子群算法求出来的控制输入不能精确地满足重构后的队形要求,且控制参数化方法是一种对初值敏感的方法,所以将它们结合起来可以很好地避免它们的不足。

3 仿真实验与结果分析

本文在MATLAB 2016b中进行仿真,计算机的配置为:Intel酷睿i7- 9750H处理器,主频2.60 GHz,内存16 GB,64位Windows 10操作系统。本文的仿真实验完成了与经典粒子群算法和改进粒子群算法的对比分析,验证了本文方法的有效性。

仿真中的参数设置如下:N=5,表示有五架无人机参与编队重构;安全距离Dsafe=10 m,通信距离D{comm}=200 m;控制参数化等分的段数p=10;选取的粒子数n=50;迭代的最大次数kmax=200;学习因子c1=c2=2.01;λ1=0.1、λ2=0.3。假设期望的重构队形为V字形。

图3、图4和图5分别为经典粒子群算法、改进粒子群算法、基于粒子群算法和控制参数化方法的多无人机编队重构过程的三维轨迹,其中:“o”表示无人机的起始位置;“*”表示终端位置。可以看到本文方法能很好地完成重构队形,改进粒子群算法次之,经典粒子群算法不能完成期望队形重构。从三种方法完成编队重构的时间来看,本文方法更有效率,其中经典粒子群算法3.754 s,改进粒子群算法4.756 s,基于改进粒子群算法和控制参数化方法3.577 7 s。

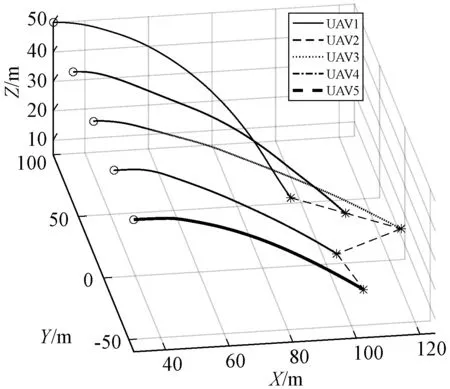
图3 经典粒子群算法编队重构轨迹

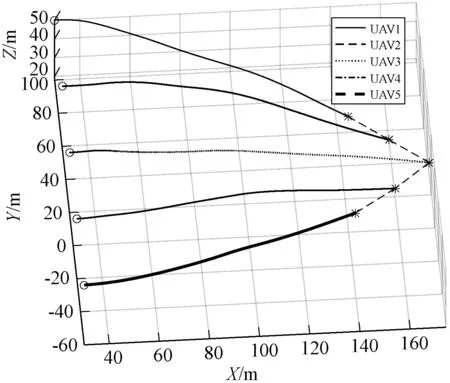
图4 改进粒子群算法编队重构轨迹

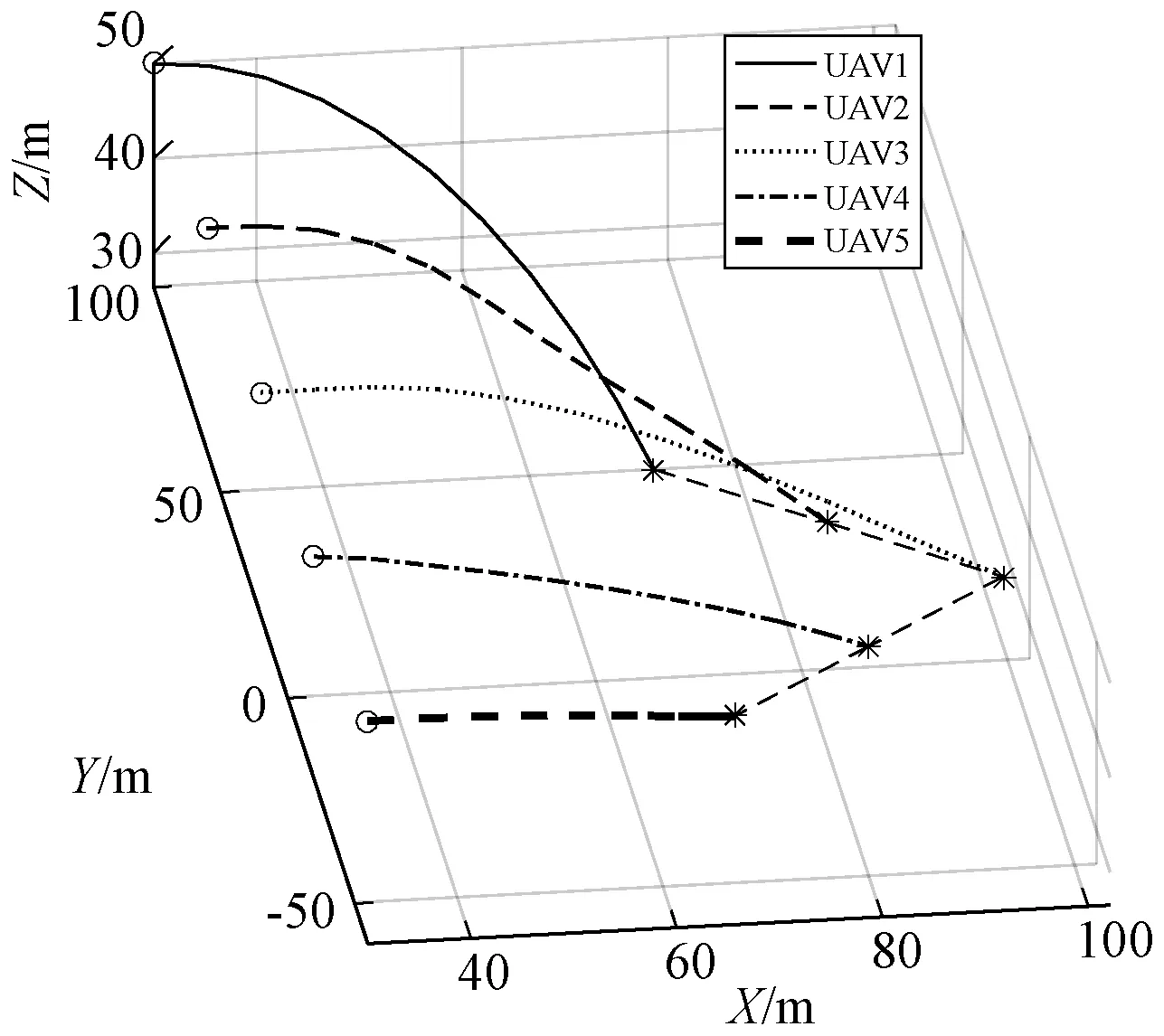
图5 基于粒子群算法和控制参数化方法的编队重构轨迹

图6、图7和图8分别是经典粒子群算法、改进粒子群算法、基于粒子群算法和控制参数化方法的水平轨迹。可以看出本文方法在水平方向能很好地完成V字形重构,而且在垂直方向能保证所有无人机在同一平面;相比较而言,改进粒子群算法基本完成V字形和大部分无人机在同一平面;然而经典粒子群算法在队形和保证无人机在同一平面上都无法满足。

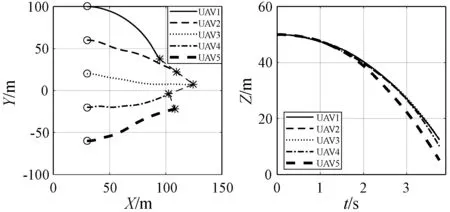
(a) XY平面轨迹 (b) Z轴方向轨迹图6 经典粒子群算法水平轨迹

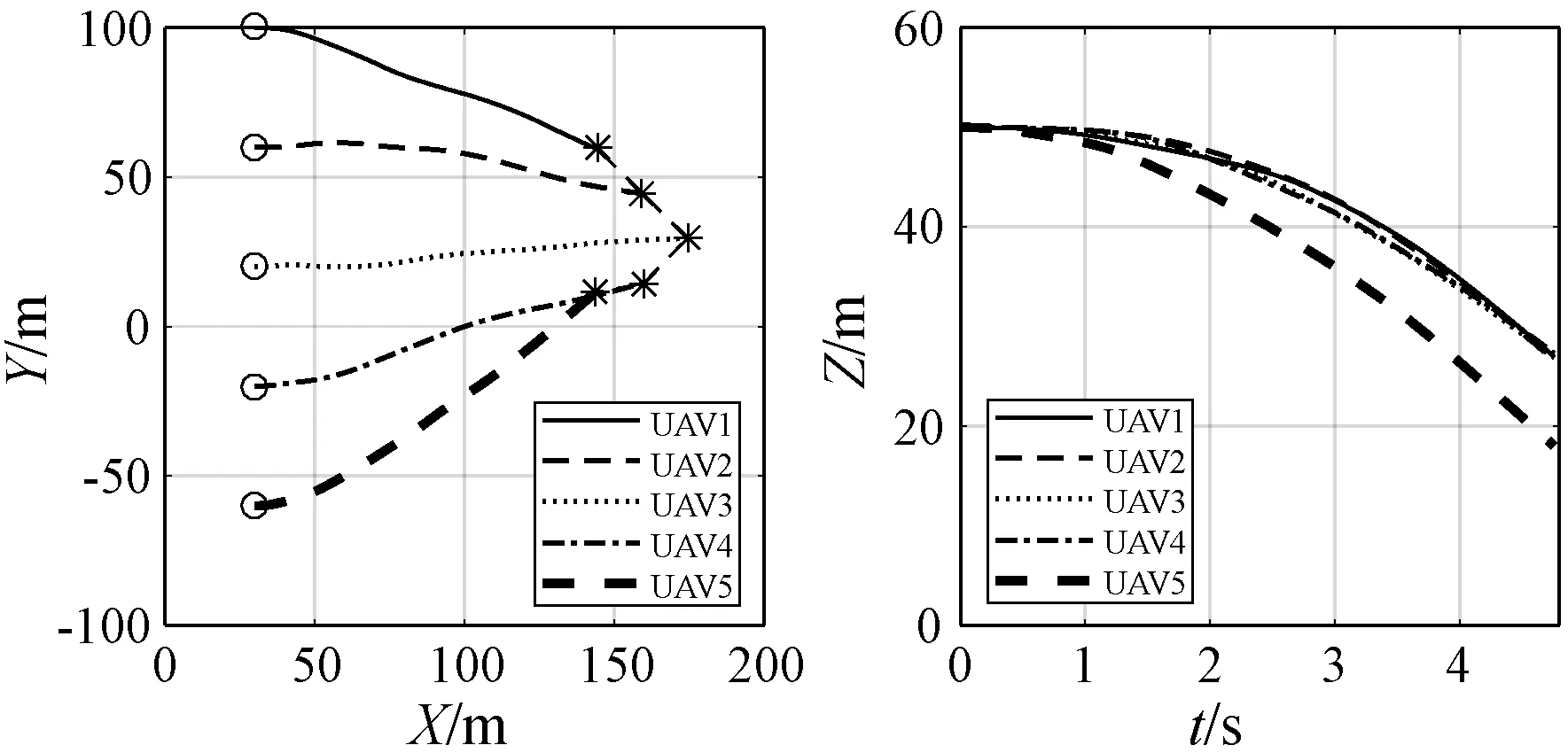
(a) XY平面轨迹 (b) Z轴方向轨迹图7 改进粒子群算法水平轨迹

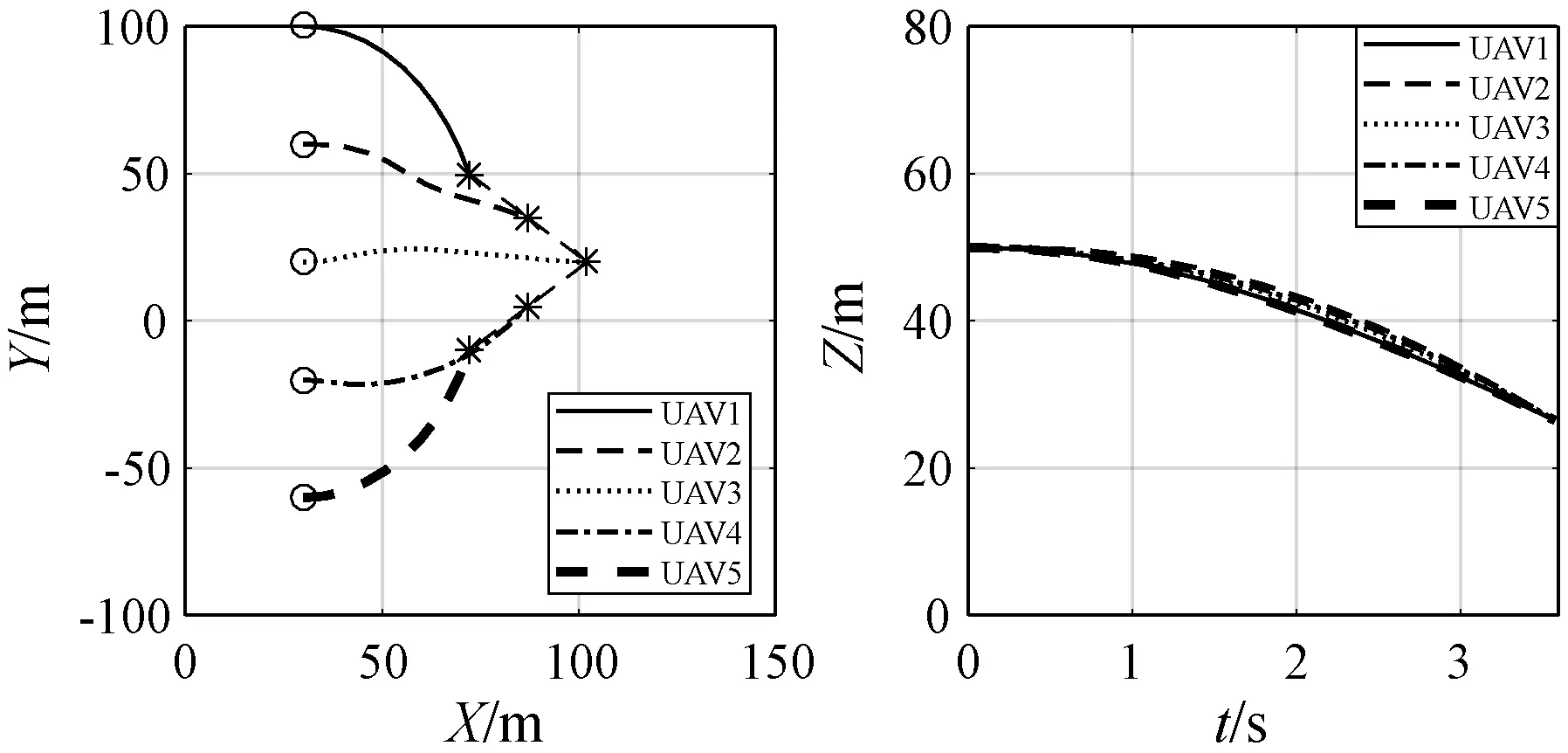
(a) XY平面轨迹 (b) Z轴方向轨迹图8 基于粒子群算法和控制参数化方法水平轨迹

图9、图10和图11分别是三种方法的多无人机编队重构过程中任意两个无人机之间的距离。可以看出,三种方法都能很好地满足约束,可以实现避免碰撞和保障通信。

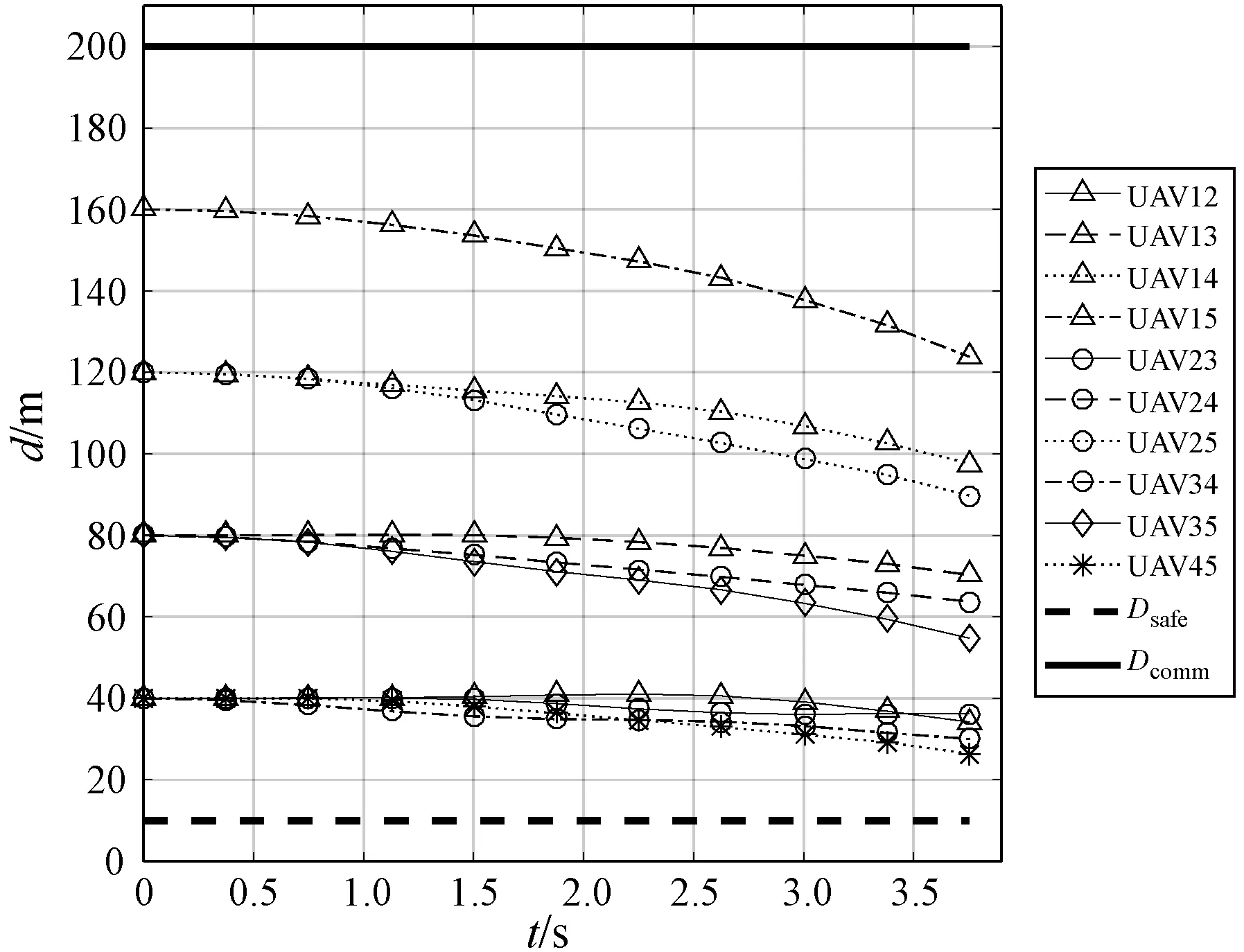
图9 经典粒子群算法的任意两个无人机之间的距离

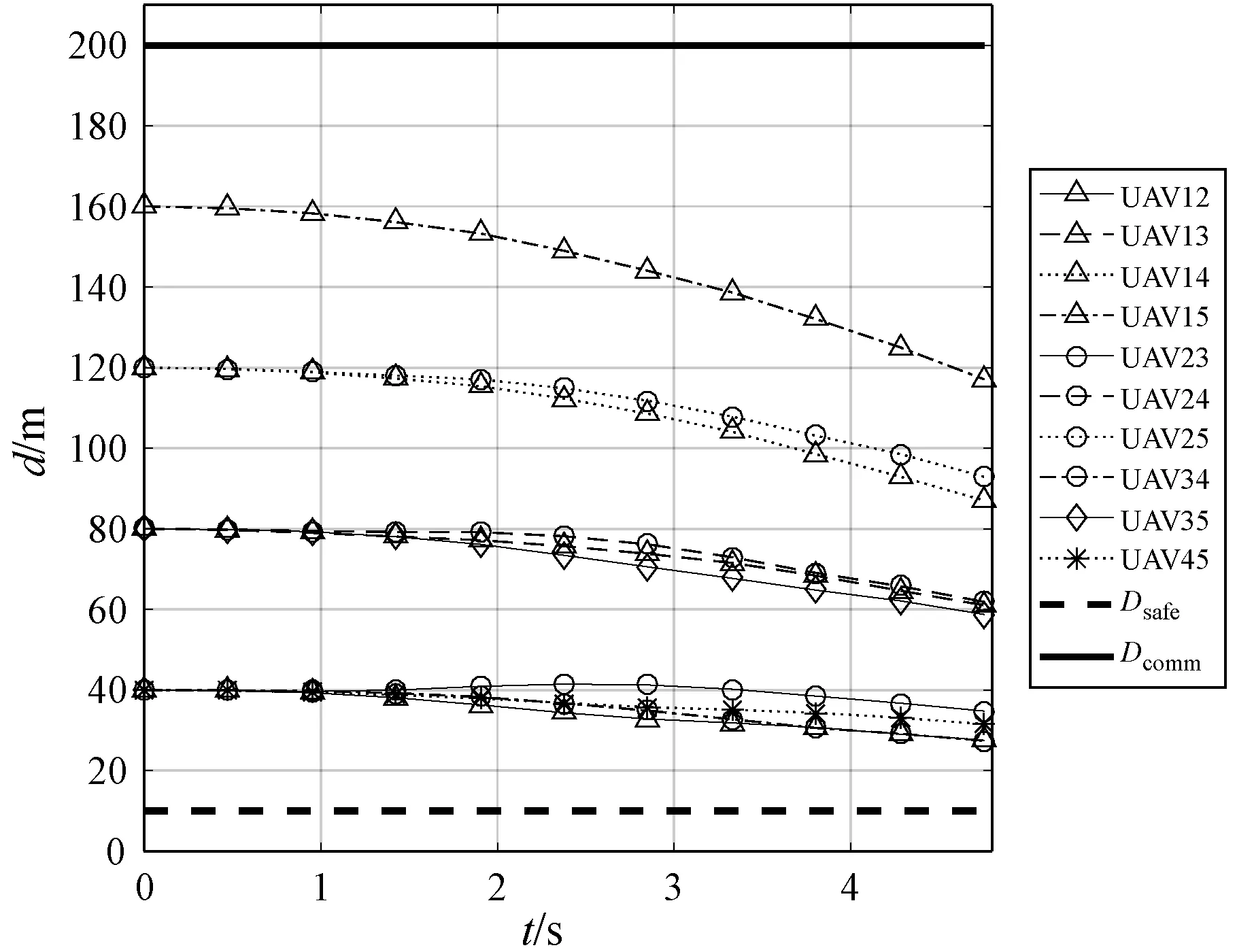
图10 改进粒子群算法的任意两个无人机之间的距离

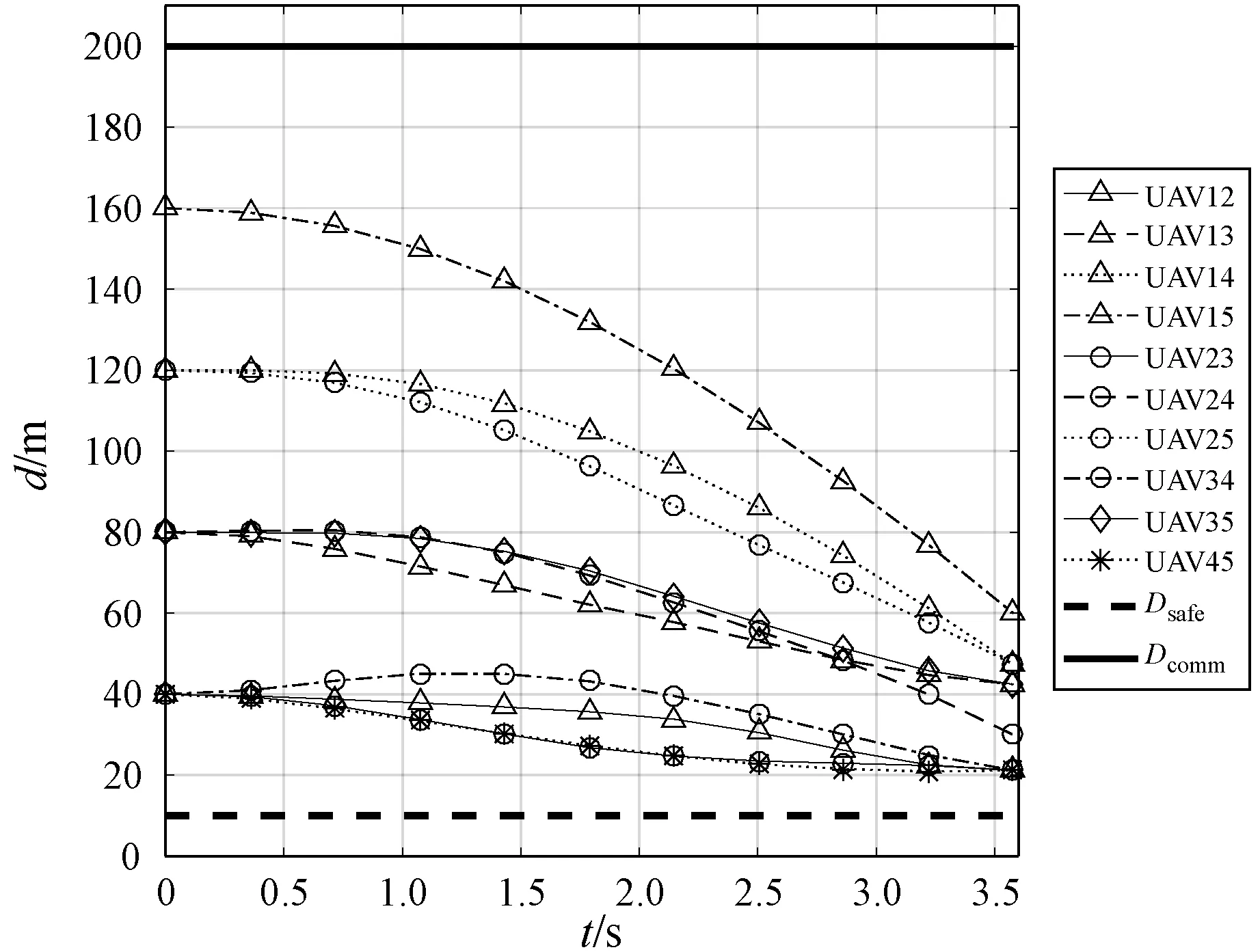
图11 基于粒子群算法和控制参数化方法的 任意两个无人机之间的距离

4 结 语

本文针对多无人机编队重构最优控制问题,给出无人机的动力学模型,考虑了无人机防碰撞约束和保证通信约束,提出一种基于粒子群算法和控制参数化的方法。通过对经典粒子群算法中的惯性权重动态的变化,改变粒子群算法前期和后期的搜索能力,提高求解的精度。利用控制参数化方法对难以处理的连续状态不等式约束进行转化,其中用到了约束转录结合局部光滑技术,使得连续状态不等式约束成为易于处理的标准约束形式。本文方法将改进粒子群算法求得的最优解作为控制参数化方法的初始值,从而避免了粒子群算法无法精确完成编队重构和控制参数化方法对初值敏感的缺点。仿真结果表明:本文方法能够很好地解决编队重构最优时间控制问题,与其他编队重构算法相比,该算法具有较高的求解精度和效率。