一种飞行模拟器坐标数据联网传输失真抑制方法

孙文柱 曹建平 孙忠云 曲建岭 于世胜

1(海军航空大学青岛校区 山东 青岛 266041) 2(中国人民解放军92212部队 山东 青岛 266109)

0 引 言

飞行模拟训练作为一种高效、安全和低成本的辅助训练方式,为操作人员提供了接近真实的训练环境,大幅提升了训练质量效益[1-3]。随着科学技术的发展,飞行器复杂度不断提高,飞行模拟训练器材经过了简单机械式模拟、机电式模拟和计算机模拟等阶段,现已发展为大规模联网式模拟训练样式[4-6]。然而模拟器组网训练过程中普遍存在网络传输坐标值失真问题,表现为模拟器中速度较快的实体(比如飞机、卫星等)坐标数值经网络传输后会发生失真现象,导致模拟器视景图像的剧烈抖动。当视点与实体距离较近时这种抖动更加明显,严重影响训练人员使用体验,降低模拟器训练效益。

针对模拟器网络传输坐标值失真问题,很多文献进行了针对性研究并给出了解决方法。陈学文等[7]为消除载人飞行器视景仿真抖动现象,将视景仿真坐标设置与飞行器动力学坐标系一致;王炜等[8]对飞参数据进行插值平滑,消除飞行回放过程中的抖动;徐勇波等[9]基于帧同步和平滑算法提出7点滑动平均方法,有效减轻了联网飞行模拟训练中观察邻近飞机时的抖动现象,曹建平等[10]在此基础上进行了改进并提出了基于加权滑动平均滤波算法的视景抖动消除方法。以上方法一定程度上减轻了数值失真的程度,但在严峻情况下仍然会出现抖动现象,且会带来数据延迟的负面影响。

卡尔曼滤波是一种基于线性系统状态方程,通过系统输入输出观测数据对系统状态参数进行最优估计的算法,可有效滤除系统中干扰和噪声的影响,在传感信号融合和飞行导航领域应用广泛[11-12]。网络传输坐标值失真问题可归结为实时仿真中延时随机性所带来的干扰,在较小的时间尺度下飞机运动方程可视为线性的,因此适用于卡尔曼滤波进行估计飞机运动状态。

1 数据抖动分析

组网训练的飞行模拟器之间一般通过“集中-分发”模式进行数据交互。如图1所示,每个飞行模拟器将飞行动力学模型输出的飞行实体位置坐标通过采样、网络传输等操作汇总到一个数据池中,汇总完成后再将所有的飞行实体位置坐标分发给各视景。

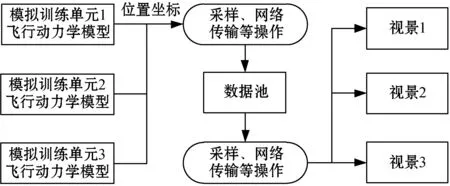
图1 组网飞行模拟器位置坐标数据传输过程

在不同的组网飞行模拟器中,位置坐标数值采用的网络技术、采样方式和网络传输的频率和步长不尽相同。因此,在整个传输过程中造成位置坐标数值失真一般由三种因素耦合产生,这三种因素包括:截断误差、存取周期不一致和网络传输丢包和乱序。

1.1 截断误差

位置数据在系统中发送和存储的类型主要有两种:单精度浮点数和双精度浮点数,根据IEEE 754二进制浮点数算术标准。单精度浮点数使用32个二进制位表示一个浮点数,包括1位符号位、8位阶码和23位尾数位,其中23位二进制尾数约相当于7位十进制有效数字,超出7位的部分为无意义数值。用单精度浮点数表示经纬度时,误差最大可达10 m以上。双精度浮点数使用64个二进制位表示一个浮点数,包括1位符号位、11位阶码和52位尾数位,使用双精度浮点数表示经纬度时精度较高,误差为10-9m量级。在飞行模拟器坐标数据网络传输和重采样过程中,为避免产生截断误差,应遵守以下原则:

(1) 避免在网络传输和重采样过程中将经纬度坐标值转为单精度浮点数。

(2) 如果网络传输工具中只提供单精度类型,可以扩展网络协议,将坐标数据分解为两个单精度值,按高低位分别发送。

1.2 存取周期不一致

网络总线是联网模拟器常用的一种数据传输方式。在网络总线数据存取时,发送方以固定周期向总线发送数据,接收方以固定周期向总线读取数据,一般来说发送数据周期和接收周期是一致的,但在程序执行过程中,发送周期和接收周期不能保证完全同步,有时会发生一个发送周期内执行两个读取操作或一个发送周期内没有执行读取操作的情况。这时,接收方的数据就会出现与上一帧同值或数值阶跃的问题,如果发送数据周期和接收周期不一致,这种问题会更加严重。为避免发生数据存取周期不同步和步长不一致产生误差,数据发送与接收应遵守以下原则:

(1) 存取周期设置为相同或成倍数关系。

(2) 使用实时操作系统。

(3) 严格的时间同步。

(4) 数据收发采用事件触发机制。

1.3 网络传输丢包和乱序

UDP网络传输协议具有不需要建立连接、传输速度快的特点,常用于模拟器网络数据发送。但由于UDP是不可靠传输协议,丢包和乱序问题不可避免。当发生丢包情况时,会导致接收端不更新数值。当发生乱序情况时,后发送的数据先到达,先发送的数据后到达,这会导致接收端数值发生脉冲抖动。为避免发生网络传输丢包和乱序问题,UDP网络传输应遵守以下原则:

(1) 数据发送频率不宜过高。

(2) 数据包长度避免过大。

(3) 优化发送与接收算法。

2 视景抖动衡量指标

目前模拟器视景抖动强弱只能用人眼定性描述,抖动程度缺乏客观定量的标准。实质上坐标数值的失真可理解为速度的突变,每次抖动都有一个速度向正反两个方向骤然增加而又回归正常的过程,此时必然伴随着加速度的瞬间大幅增加。飞机在正常飞行过程中,由于飞机设计和人体承受极限因素的限制,一般最高过载不超过9个G。检测坐标数值失真程度时,可将坐标数值取二阶导数得到加速度值,当加速度值超出正常范围,可认为数据发生了失真,且加速度峰值越大失真程度越大。因此坐标数值取二阶导数得到的加速度值可作为衡量视景抖动程度的指标,加速度峰值表示数据失真的程度,同时也表征视景抖动的剧烈程度。在实际测试过程中发现,当加速度峰值低于200 m/s2时,视景抖动不明显,当加速度峰值高于200 m/s2并低于1 000 m/s2时,视景有轻微抖动,当加速度峰值高于1 000 m/s2时,视景抖动剧烈。

3 基于卡尔曼滤波的飞行动力学数据抖动抑制方法

卡尔曼滤波通过输入输出观测数据建立线性系统状态方程,并能够给出下一时刻系统状态的最优估计[13]。本节使用卡尔曼滤波建立飞行动力学模型的系统状态方程,并通过滤波估计得出下一时刻飞行动力学数据估计值,当网络传输的飞行动力学数据发生异常时,卡尔曼滤波方法可以给出最优估计,方法如下:

包含扰动的飞机飞行动力学模型可以通过如下公式表示:

式中:xk和xk+1分别为k时刻和k+1时刻飞机状态;uk为k时刻飞机运动参数;G为单位矩阵。

xk=[Px(k)Vx(k)Py(k)Vy(k)Pz(k)Vz(k)]T

(2)

uk=[ax(k)ax(k)ay(k)ay(k)az(k)az(k)]T=

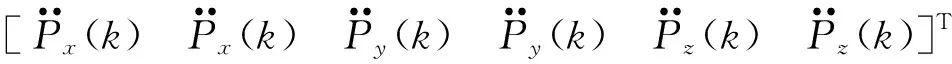
(3)

A为状态转移矩阵:

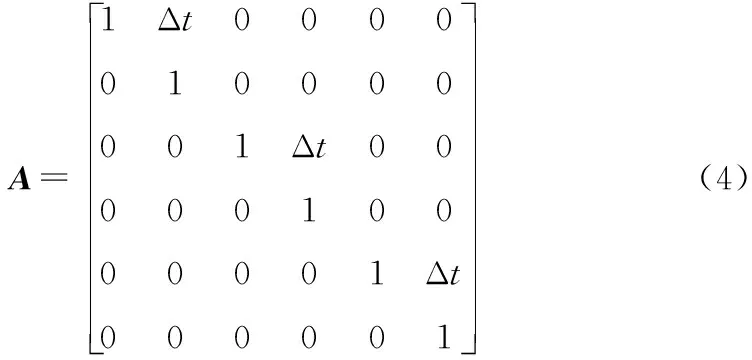
式中:Δt为仿真步长。

B为控制矩阵:

H为观测矩阵:

wk和vk为系统扰动噪声,服从正态分布:

wk～N(0,Q)

(7)

vk～N(0,R)

(8)

系统当前状态的预测估计方程为:

预测协方差为:

卡尔曼增益为:

滤波估计为:

协方差更新公式表示为:

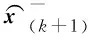
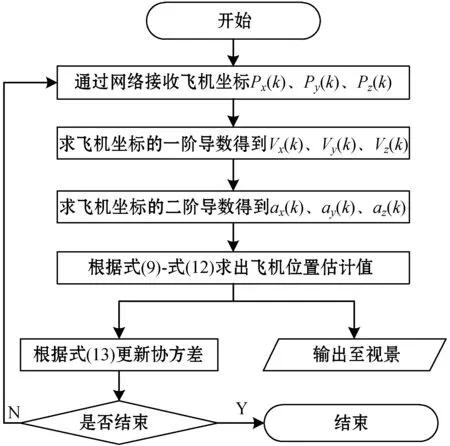
图2 飞机坐标数据卡尔曼滤波方法流程

4 实验与结果分析

4.1 实验一

选取某型战斗机模拟器动力学模型记录的一段直线飞行坐标数据作为真实值,人工加入总采样点数5%的奇异值仿真观测值。分别使用7点滑动平均法[9]和卡尔曼滤波法对带有奇异值的飞行数据进行处理。图3给出了飞机经度真实值、观测值随时间变化的曲线和两种处理方法的处理结果。观测值中,6.17 s处是一个奇异值,此处观测值与真实值产生了较大偏差,其他位置上观测值与真实值相同。两种数据处理方法的结果与真实值都有整体上的偏移,这是由于数据经算法处理后,飞行数据产生了延迟。可以看出,7点滑动平均法处理后的数据与真实值相比偏差较大而卡尔曼滤波法的结果延迟较小。观测值中奇异值出现以后,对数据处理结果产生了影响,卡尔曼滤波法处理后的数据产生了较小的波动,7点滑动平均法处理后的数据波动较大,7个采样点后数据恢复正常。

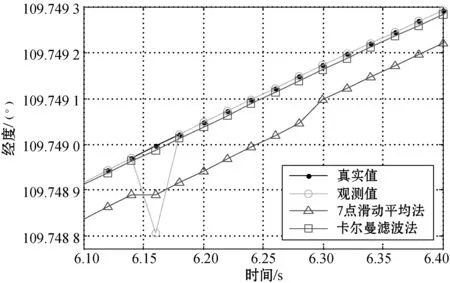
图3 飞机经度随时间变化曲线

图4显示了观测值和两种数据处理方法结果的距离误差。可以看出,奇异值出现以前,两种方法处理后的数据都有不同程度的距离误差,卡尔曼滤波法处理后的数据距离误差较小,为0.56 m,而7点滑动平均法处理后的数据距离误差较大,为10.58 m。幅度为20 m的奇异值出现后,对两种数据处理方法的结果都产生了影响,卡尔曼滤波法处理后的数据增大了0.42 m的偏差,而7点滑动平均法处理后的数据产生了2.86 m的偏差。

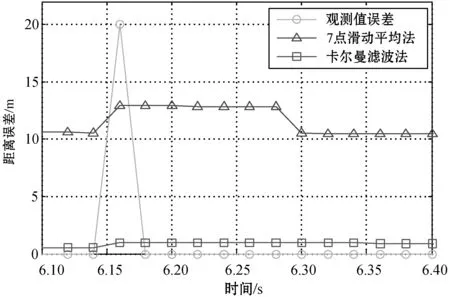
图4 数据处理结果的距离误差

图5显示了观测值和两种数据处理方法结果的加速度值,奇异值出现以后,观测值加速度波动很大,为104数量级,此时模拟器画面会出现剧烈的抖动。经7点滑动平均法处理后加速度波动降低到103数量级,此时模拟器画面仍会出现明显的抖动,而且7个采样点后又出现了一次103数量级的波动。经卡尔曼滤波法处理后加速度波动降为102数量级且波动只出现一次,随后迅速收敛,此时模拟器画面抖动不明显。

图5 数据处理结果的加速度值

4.2 实验二

选取某型战斗机模拟器动力学模型记录的直线飞行、垂直筋斗、水平盘旋3种状态的3段坐标数据,每段数据1 000个采样点,第一次在坐标采样数据中人工加入50个奇异值作为仿真观测值,第二次加入功率为20 dBw的白噪声作为仿真观测值。分别使用7点滑动平均法和卡尔曼滤波法对带有奇异值的飞行数据进行处理。并对处理结果的均方根误差进行比较。均方根误差E的计算公式为:

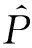
表1给出了加入奇异值的观测值和两种数据处理方法结果的均方根误差。可以看出,加入奇异值时,3种动作观测值的均方根误差介于2.5到2.8之间。经7点滑动平均法处理后均方根误差不仅没有减少,反而增大明显,尤其是直线飞行时,这种增大更为明显。这是因为该方法产生了较大的延迟,而延迟会产生均方根误差。水平盘旋时飞机做圆周运动,圆周运动在一个方向上的投影是往复运动,往复过程中会补偿一部分均方根误差,因此水平盘旋时7点滑动平均法的均方根误差略小;垂直筋斗的情况则介于直线飞行和水平盘旋之间。数据经过卡尔曼滤波法处理后均方根误差能明显减少,数据均方根误差由2.5到2.8之间降到0.5以下。

表1 加入奇异值时均方根误差

表2给出了加入白噪声的观测值和两种数据处理方法结果的均方根误差。可以看出,加入白噪声时,3种动作观测值的均方根误差较大,误差值处于10±0.15区间。经7点滑动平均法处理后直线飞行和垂直筋斗的均方根误差值略有增大,水平盘旋的均方根误差值略有减少。数据经过卡尔曼滤波法处理后均方根误差能明显减少,数据均方根误差由10±0.15降至2.5以下。

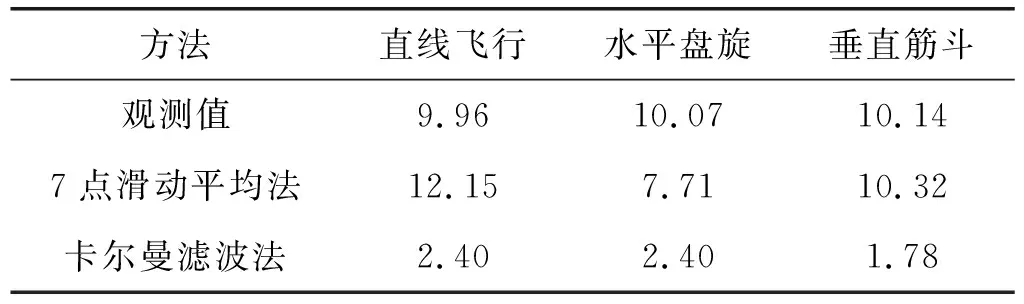
表2 加入白噪声时均方根误差

5 结 语

本文在深入分析飞行模拟器网络传输数值失真原因基础上给出了避免模拟器传输数据失真的措施,并给出衡量数据失真程度的有效度量——由坐标数值经二阶求导得出的加速度值。此外,在飞行动力学建模基础上,本文提出一种基于卡尔曼滤波的飞行模拟器坐标数据联网传输失真抑制方法,随后的比较实验证明,该方法延迟较小,能大幅减小失真数据的均方根误差,最大程度上还原飞行模拟器坐标数据真实值,是解决飞行模拟器中视景系统中实体抖动问题的有效方法。