基于改进相关向量机的模拟电路故障预测

王 力 石立超

(中国民航大学 天津 300300)

0 引 言

现阶段,模拟电路在控制、通信和导航等电子系统中得到了广泛应用,随着对电子系统可靠性要求不断提高,模拟电路作为电子系统的重要组成部分,其故障预测方法已成为了当下的研究重点[1-2]。

当前故障预测方法主要包括基于物理模型的方法和基于数据驱动的方法[3-5]。基于物理模型的方法通过分析实际特征参数与物理模型仿真的特征参数之间的残差来判断系统的状态,逻辑推理严密,诊断说服力强[6]。但随着电子设备越来越复杂,物理模型的建立难度也越来越大。基于数据驱动的方法以测试和状态监测数据为对象,估计对象系统未来的状态演化趋势,从而避免了基于物理模型方法的缺点。其中,相关向量机(Relevance Vector Machine,RVM)具有参数设置简单、稀疏度高、概率式输出以及核函数不受Mercer定理约束等特点,已在模拟电路故障预测[7]、锂电池剩余寿命预测[8-10]以及列车牵引系统剩余寿命预测[11]中表现出良好的效果。但是,直接采用RVM算法进行预测,预测精度较低,且预测结果易受训练样本影响[12]。

鉴于此,本文针对模拟电路故障预测中的关键问题,提出了一种基于离散灰色多核RVM的模拟电路故障预测方法,用于预测模拟电路的剩余使用性能(Remain Useful Performance,RUP)。在提取被测电路(Circuit Under Test,CUT)的故障特征数据之后,首先将传统RVM中单个核函数改进为多个不同核函数组合形成混合核函数,然后利用量子方法改进人工蜂群算法提升其优化效果以对各个核函数的权重因子寻优,从而提高算法的泛化性能及预测精度。最后利用离散灰色模型与多核相关向量机相结合,提升算法的长期趋势预测性能。本文以Sallen-Key带通滤波电路和Biquad低通滤波电路两个国际上最常用的验证预测方法性能的基准电路[1]为实验对象,验证所提故障预测方法性能的优劣。

1 模拟电路故障特征提取与预处理

在模拟电路故障预测的过程中,故障特征提取与预处理是一个重要环节,其目的在于更加准确地描述影响电路性能退化的元器件的老化过程。

1.1 故障特征提取

模拟电路中电阻、电容等元器件极易发生故障[1],对CUT输入扫频信号,当这些元器件性能衰退时,具体表现为其参数值发生单向偏离,其电路输出响应就会发生变化,如图1所示。

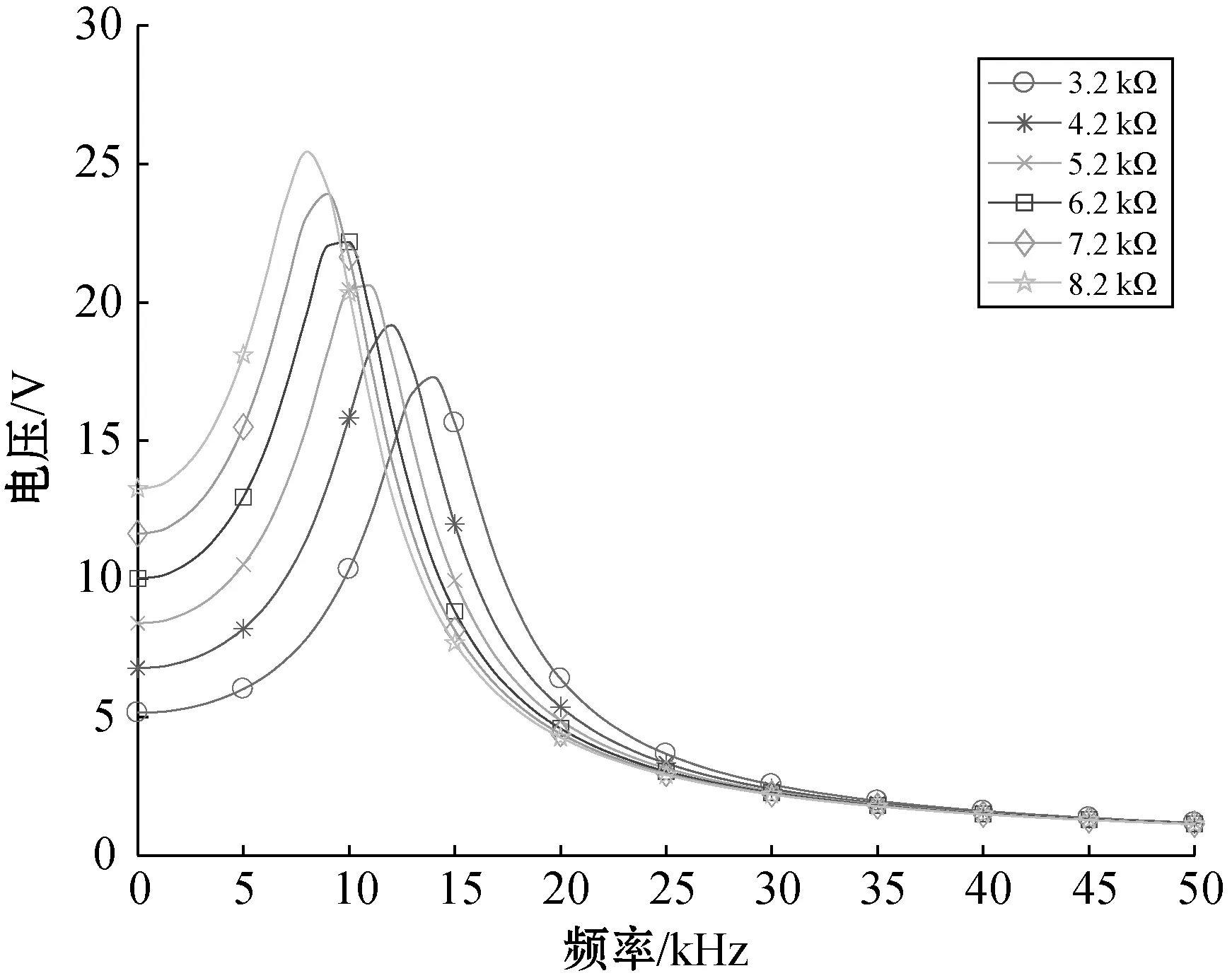
图1 不同电阻值的电路输出响应

在不同参数下输出频率响应中均匀地提取不同频率下的电压作为特征向量,如图2所示。

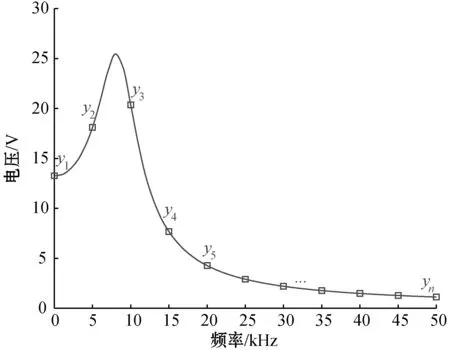
图2 特征提取过程

特征向量表示为:

Y=[y1,y2,…,yn]

(1)

式中:y1,y2,…,yn是CUT在同一元器件参数值下的不同频率响应,即电压,n为特征数量。

1.2 故障特征预处理

在提取故障特征之后,需要对特征向量采用皮尔逊相关系数(Pearson Product-moment Correlation Coefficient,PPMCC)方法进行预处理,处理后的数据用来表示元器件的健康度[3]。

PPMCC用于表示两个向量间的相关程度,是衡量两个向量相似度的一种方法,其计算公式如下:

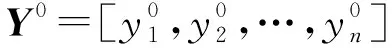
当元器件无故障时,其参数值等于标准参数值,即Y0=Yh,此时计算出的PPMCC为1,表示元器件健康度为1,当元器件发生性能衰退时,其参数值偏离标准参数值,即Y0≠Yh,计算出的相关度也随之变小,表示元器件的健康度下降,即元器件的性能发生衰退。

2 模拟电路RVM故障预测算法改进

在构建模拟电路故障预测模型时,不仅要考虑预测模型的预测精度问题,还要考虑其泛化性、适用性以及长期趋势预测的稳定性问题。鉴于此,本文提出的故障预测算法结合RVM算法、人工蜂群算法及离散灰色模型的特点,并提出了以下三个改进之处。

(1) 针对单核RVM算法表达能力受限,易于忽略故障特征中的关键信息从而导致泛化性能差以及预测精度低的问题,提出了多核RVM算法。通过对五个不同的核函数组合形成混合核函数以更多地获取故障特征中的有用信息,从而增强RVM算法的泛化性能和预测精度。其中,多核RVM中每个核函数的权重因子由人工蜂群算法寻优生成。

(2) 针对传统的人工蜂群算法在优化过程中对于离散变量的优化效果较差的问题,本文提出了量子人工蜂群优化方法(Quantum-behaved Artificial Bee Colony,QABC),使全局搜索能力得到加强,并且有效地解决了对离散变量优化效果较差的问题。然后对RVM每个核函数的权重因子寻优,更有效地提高了RVM算法的预测精度。

(3) 针对RVM长期预测精度低的问题,本文提出将RVM算法与离散灰色模型相结合,利用离散灰色模型长期预测精度高的特点,提升RVM长期预测能力。

2.1 RVM算法改进

故障预测属于时间序列多步预测问题,本质上是回归问题,所以本文对相关向量回归方法进行改进。其中RVM训练算法采用MacKay迭代估计法。

t=y(x)+ε

(3)

式中:y(x)为非线性函数;ε为均值为0,方差为σ2的高斯噪声。

相关向量回归的数学表达式为:

t=φω+ε

(4)

式中:ω=(ω0,ω1,…,ωN)T为相关向量回归的权值;φ=(φ0,φ1,…,φN)T为核函数矩阵,且φ(x)=[1,K(x,x1),…,K(x,xN)],K(x,xi)为核函数。

本文选取的核函数分别为高斯核函数、指数核函数、拉普拉斯核函数、多项式核函数和Sigmoid核函数,将五个核函数进行线性组合,QABC算法来优化各个核函数的权重系数。本文首先采用单核RVM模型进行训练,得到效果较好的超参数,然后对各个核函数进行线性组合。

其中,高斯核函数为:

指数核函数为:

拉普拉斯核函数为:

多项式核函数为:

K4(x,xi)=(axTxi+c)d

(8)

Sigmoid核函数为:

K5(x,xi)=tanh(axTxi+c)

(9)

通过对多个核函数进行线性组合,可以更全面地描述元器件的性能衰退过程。五个核函数线性组合的构建方法为:

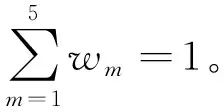
(11)

式中:t=(t1,t2,…,tN)T。

如果直接对权重ω进行最大似然估计,会存在过拟合现象。因此,在权重ω上定义一个零均值高斯先验分布:

(12)

式中:α=(α0,α1,…,αN)为N+1个超参数,与权重ω相对应。

在稀疏贝叶斯理论下,当存在一组新的输入数据时,基于稀疏贝叶斯理论下的预测可表示为:

p(tN+1|t)=∭p(tN+1|ω,α,σ2)p(ω,α,σ2|t)dωdαdσ2

(13)

式中:tN+1为新的输入数据的目标值。

对式(13)进行分解,得到:

p(ω,α,σ2|t)=p(ω|t,α,σ2)p(α,σ2|t)

(14)

参数的后验分布在先验分布和似然分布的基础上应用贝叶斯推理,得到:

得到权重的后验方差和均值分别为:

φ=(σ-2φTφ+A)-1

(16)

μ=σ-2φφTt

(17)

式中:A=diag(α0,α1,…,αN)。

对式(11)中参数进行边缘积分,得出最合适的超参数后验分布式:

输入的一组新的数据x*,其输出t*预测均值和方差分别为:

t*=μTφ(x*)

(19)

2.2 人工蜂群算法改进

人工蜂群算法是一种模拟自然界中蜜蜂搜索蜜源过程的群智能算法[13]。将所有蜜源的五维向量设置为多核RVM算法中五个核函数的权重因子w1,w2,…,w5,在每次迭代过程中,根据适应度对蜜源的优劣进行比较,通过寻找更优蜜源来优化权重因子,直至达到最大迭代次数为止。

用一串量子位表示量子蜜蜂的位置[14],一个量子位为(a,b)T,其中a2+b2=1,第i只量子蜜蜂的位置为:

式中:i={1,2,…,BN},BN为种群规模。

对量子蜜蜂位置的更新通过量子旋转门来实现。第i只量子蜜蜂的位置的第n个量子位vin可以表示为:

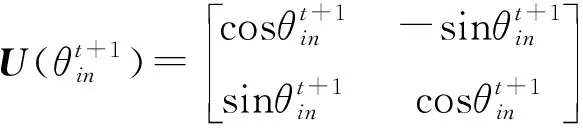
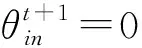
整个蜂群主要包括两个角色:量子引领蜂和量子侦察蜂,并且数目相同。量子引领蜂的数量和食物源的数量相等,每个量子引领蜂位置都对应一个由字符串0或1组成的蜜源,用zi=(zi1,zi2,…,zim)来表示第i个蜜源的位置,m表示优化问题的维度,其中第i个食物源的第d个量子位zid可以表示为:

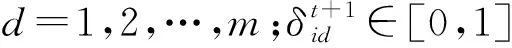
假设当前第i只量子蜜蜂的局部最优位置为pi=(pi1,pi2,…,pim),整个蜂群当前全局最优位置为pg=(pg1,pg2,…,pgm)。

量子引领蜂主要依据当前局部最优位置和蜂群全局最优位置来进行位置的更新。具体表示为:

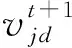
通过对量子引领蜂进行择优,然后利用其局部最优位置来确定量子侦察蜂位置的更新。第j只量子引领蜂被选择的概率为:

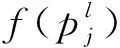
量子侦察蜂量子位的更新表示如下:

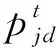
反复进行上述量子引领蜂、量子侦察蜂的量子位更新过程,直到算法达到迭代次数limit,输出全局最优解。

综上所述,给出量子人工蜂群算法的流程如图3所示。

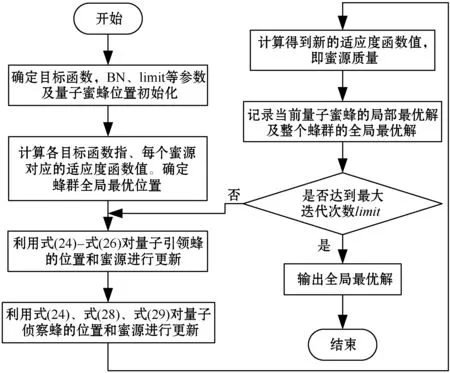
图3 量子人工蜂群算法流程

2.3 离散灰色多核RVM故障预测算法

离散灰色模型具有趋势预测精度高、稳定性强的特点[15],将离散灰色模型与多核RVM相结合可以提高预测精度。离散灰色多核RVM预测模型的构建包括以下五个阶段。

(1) 初始化阶段。将元器件健康度数据分为训练数据和测试数据,初始化多核RVM参数,包括每个核函数经QABC算法寻优得到的权重因子,MacKay迭代估计法的最大循环次数、收敛条件等。

(2) 离散灰色模型的建立。假设原始训练数据序列为:

X(0)={x(0)(1),x(0)(2),…,x(0)(n)}

则灰色微分方程为:

x(1)(k+1)=r1x(1)(k)+r2

(30)

由于训练数据X(0)为非负序列,所以其一次累加生成序列为:

X(1)={x(1)(1),x(1)(2),…,x(1)(n)},其中x(1)(k)按照下式来计算:

式中:k=1,2,…,n。

将X(1)代入下式:

Z=Br

(32)

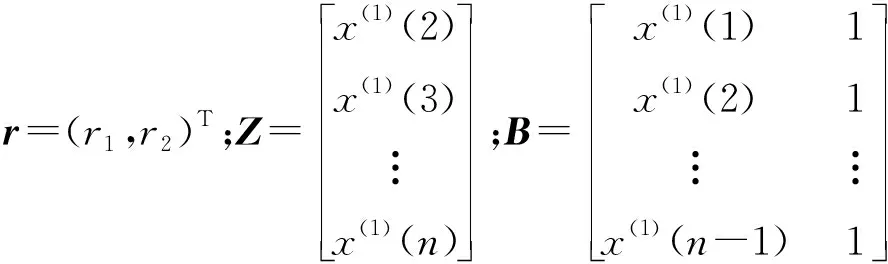
采用最小二乘法估计灰色微分方程x(1)(k+1)=r1x(1)(k)+r2,得到方程系数为:

r=(BTB)-1BTZ

(33)

令x(1)(1)=x(0)(1),则一次累加生成序列的估计值为:

式中:k=2,3,…,n。

通过还原得到离散灰色预测模型:

将式(34)代入式(35)得到离散灰色预测模型:

式中:k=2,3,…,n。

(3) 多核RVM建模。用式(36)对训练数据进行预测,将预测结果输入多核RVM,原始训练数据为多核RVM的输出,采用MacKay迭代估计法训练多核RVM模型,得到多核RVM回归预测模型。

(4) 预测模型测试。将测试数据输入离散灰色模型,得到预测值输入多核RVM模型,得到最终预测结果并判断预测值是否小于设定的故障阈值,若小于,则将预测值转换为RUP;否则,将对多核RVM模型进行更新。

(5) 多核RVM模型更新。首先,采用新陈代谢法,用阶段(4)得到的预测值更新训练数据,得到新的训练数据。然后,计算新训练数据与原始训练数据的相关度,若相关度大于0.9,则返回(4)继续预测;否则,返回(3)更新多核RVM模型,并进行预测。

综上所述,离散灰色多核RVM故障预测算法的流程如图4所示。

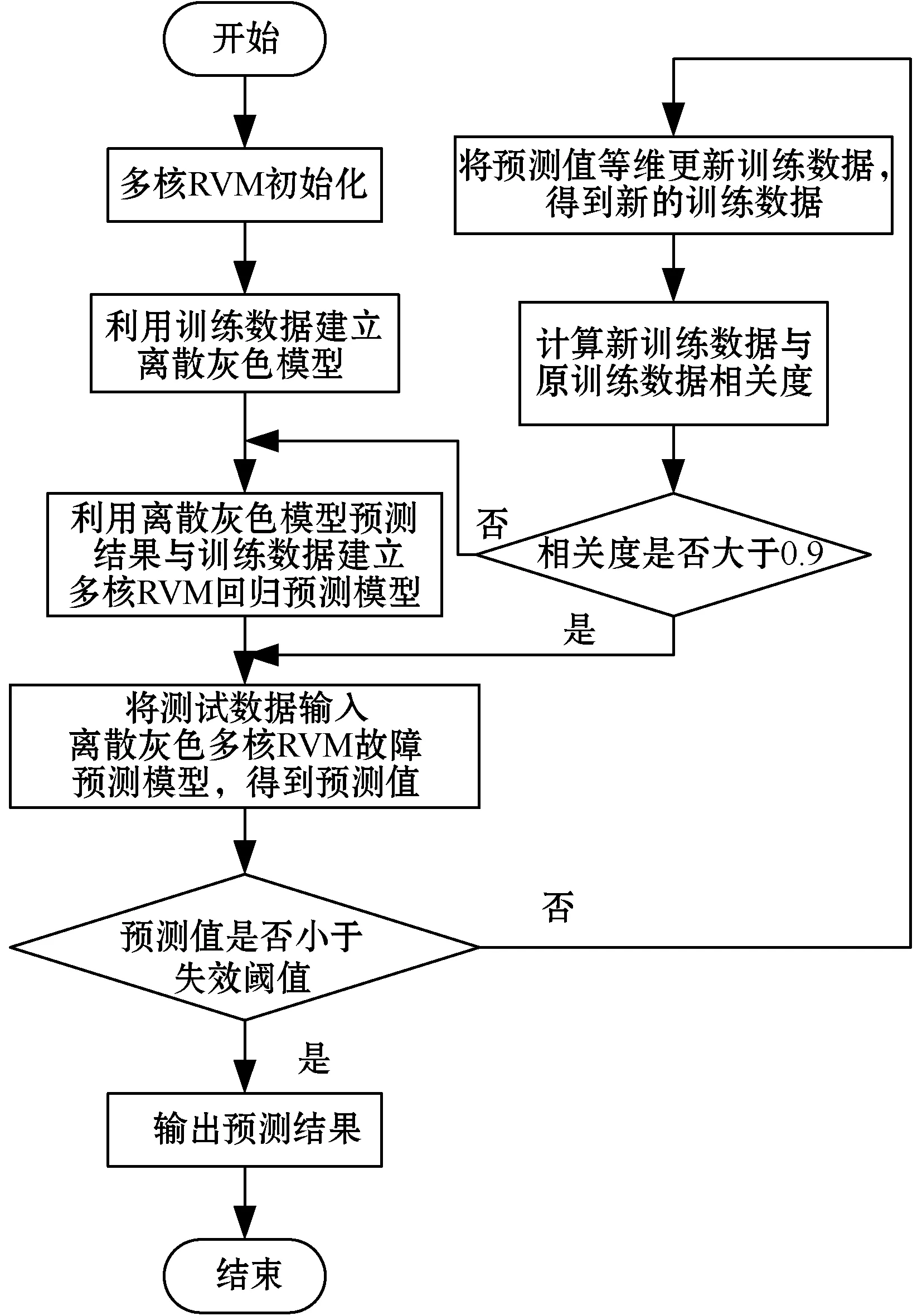
图4 离散灰色多核RVM故障预测算法流程

3 仿真实验及分析

模拟电路的故障以单一故障情形为主,且单一故障情形预测方法亦可拓展到多重故障情形[1],本文以单一故障情形为例进行实验验证,并采用图5、图6所示Biquad低通滤波电路和Sallen-Key带通滤波电路两个国际常用的验证电路[1]为例对所提出的故障预测方法进行仿真实验及分析。

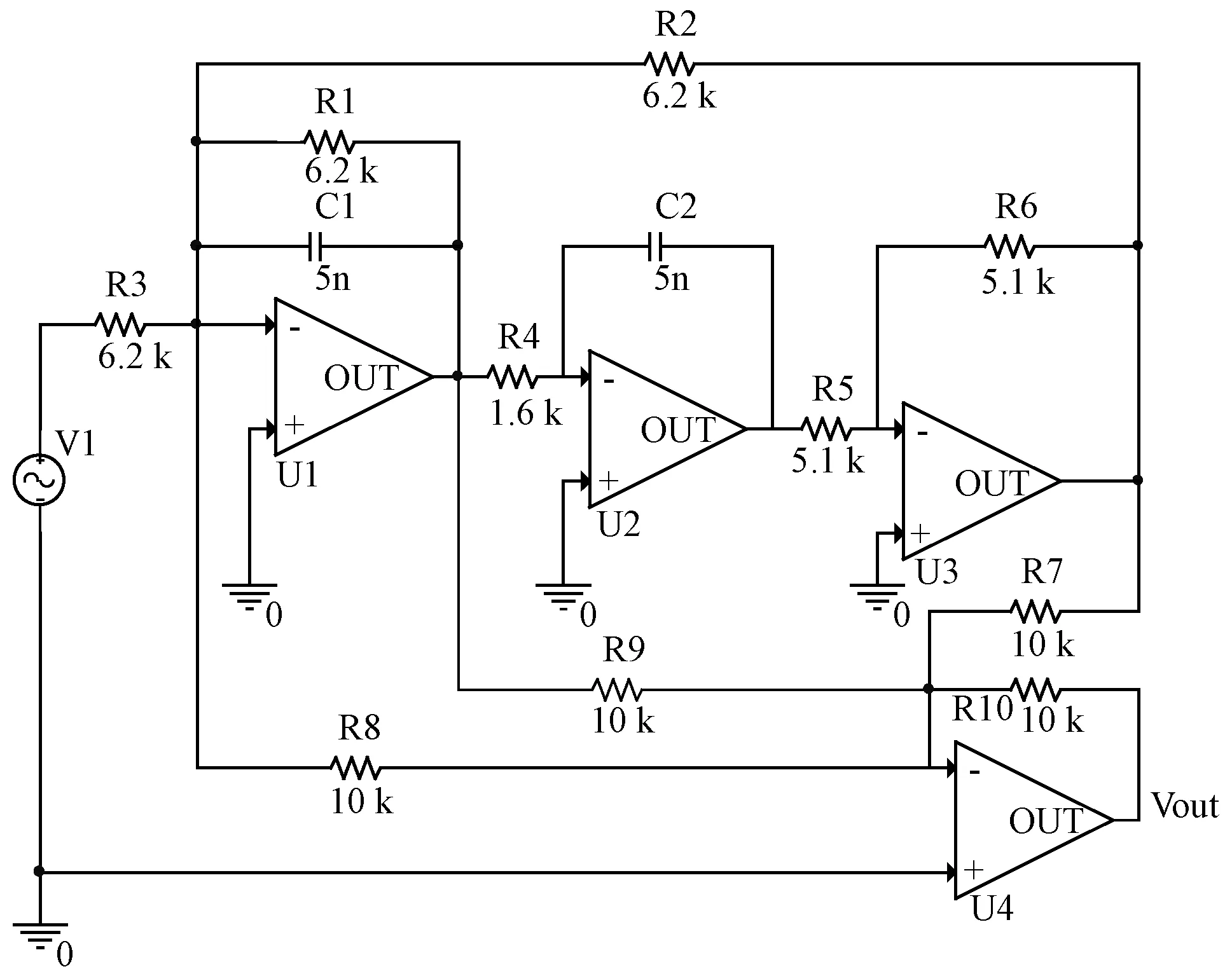
图5 Biquad低通滤波电路

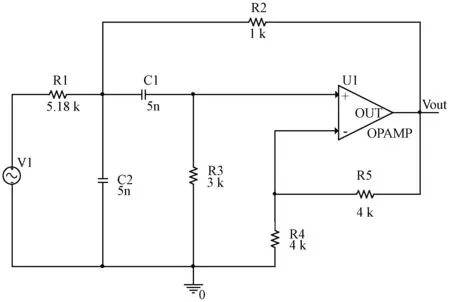
图6 Sallen-Key带通滤波电路

本次实验步骤如下:

步骤1将扫频信号输入CUT,在CUT输出端均匀地提取每个元器件不同参数下的频率响应信号;

步骤2利用PPMCC方法对各个元器件的频率响应信号进行计算得到每个元器件的健康度,并作为样本数据;

步骤3将样本数据分为训练数据和测试数据;

步骤4利用QABC算法优化生成多核RVM核函数的权重因子;

步骤5将训练数据输入离散灰色多核RVM建立故障预测模型;

步骤6利用测试数据进行故障预测得到预测结果,计算RUP及各项评价指标。

仿真实验以OrCAD Capture 16.6和MATLAB R2016b为实验平台,验证电路由OrCAD Capture 16.6搭建,仿真数据由Pspice仿真后采集得出,方法的验证、编译及实验结果由MATLAB R2016b得到。

3.1 实验参数设置

当元器件参数值偏离标称值50%该元器件发生故障,可以计算出元器件发生故障的时间点为:

TF=|VF-Vno|/V0

(37)

式中:TF为元器件发生故障的时间点;VF为元器件发生故障的参数值;Vno为元器件无故障的参数值(标称值);V0为元器件每个时间点的参数变化量。

用Vend来表示本次实验中元器件最终的参数值,则每个元器件的时间点总数Tend为:

Tend=|Vend-Vno|/V0

(38)

选择图5电路中的R2、C1和图6电路中的R3为实验对象,假设R2、C1和R3的参数值在性能衰退期间为均匀变化,每次变化在时间上对应一个时间点。当R2参数值不断升高,从6.2 kΩ升至9.92 kΩ,每次均匀增加6.2 Ω,共600个时间点;C1参数值不断升高,从5 nF升至8 nF,每次均匀增加0.005 nF,共600个时间点;R3参数值不断升高,从3 kΩ升至4.8 kΩ,每次均匀增加3 Ω,共600个时间点,R2、C1和R3在第500个时间点发生故障。在使用Pspice仿真过程中,设定Biquad低通滤波电路交流扫频激励信号的起始频率为1 Hz,终止频率为50 kHz;Sallen-Key带通滤波电路交流扫频激励信号的起始频率为1 Hz,终止频率为100 kHz。表1记录了本次实验元器件各项实验参数。

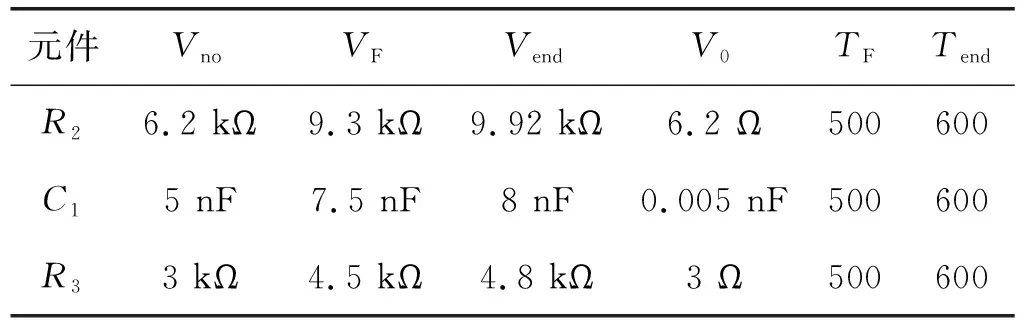
表1 C1和R3实验参数

3.2 实验过程

对CUT输入扫频信号,在输出端提取频率响应信号,应用式(2)计算出R2、C1和R3在各个时间点的健康度,可以得出R2、C1和R3在第500个时间点的故障阈值分别为0.919 534 280 701 682、0.915 965 952 985 941和0.956 998 900 194 065,三者稍有不同,原因在于每个元器件对扫频信号的灵敏度不同,灵敏度越大,则故障阈值越小。

上述结果是在理想条件下得出,然而模拟电路在实际运行过程中会受到器件容差、温度及外界应力等干扰,测量过程也会存在误差。因此,本文在R2、C1和R3的健康度中添加2%的高斯白噪声以模拟电路的实际运行时的情形[17]。该方法已经过文献[17]验证可以模拟实际电路测量时的情形,如图7、图8和图9所示。

图7 添加噪声的R2健康度

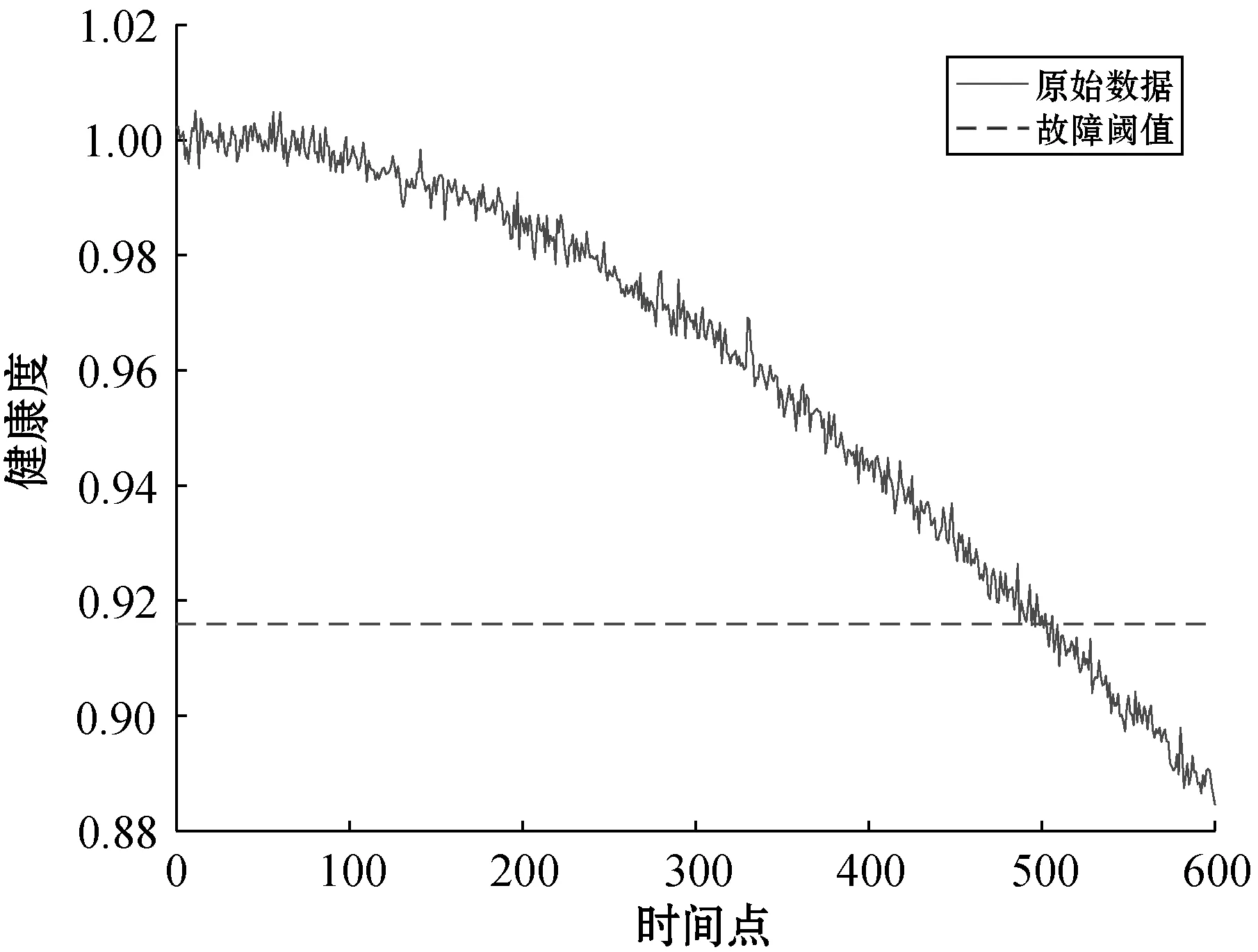
图8 添加噪声的C1健康度

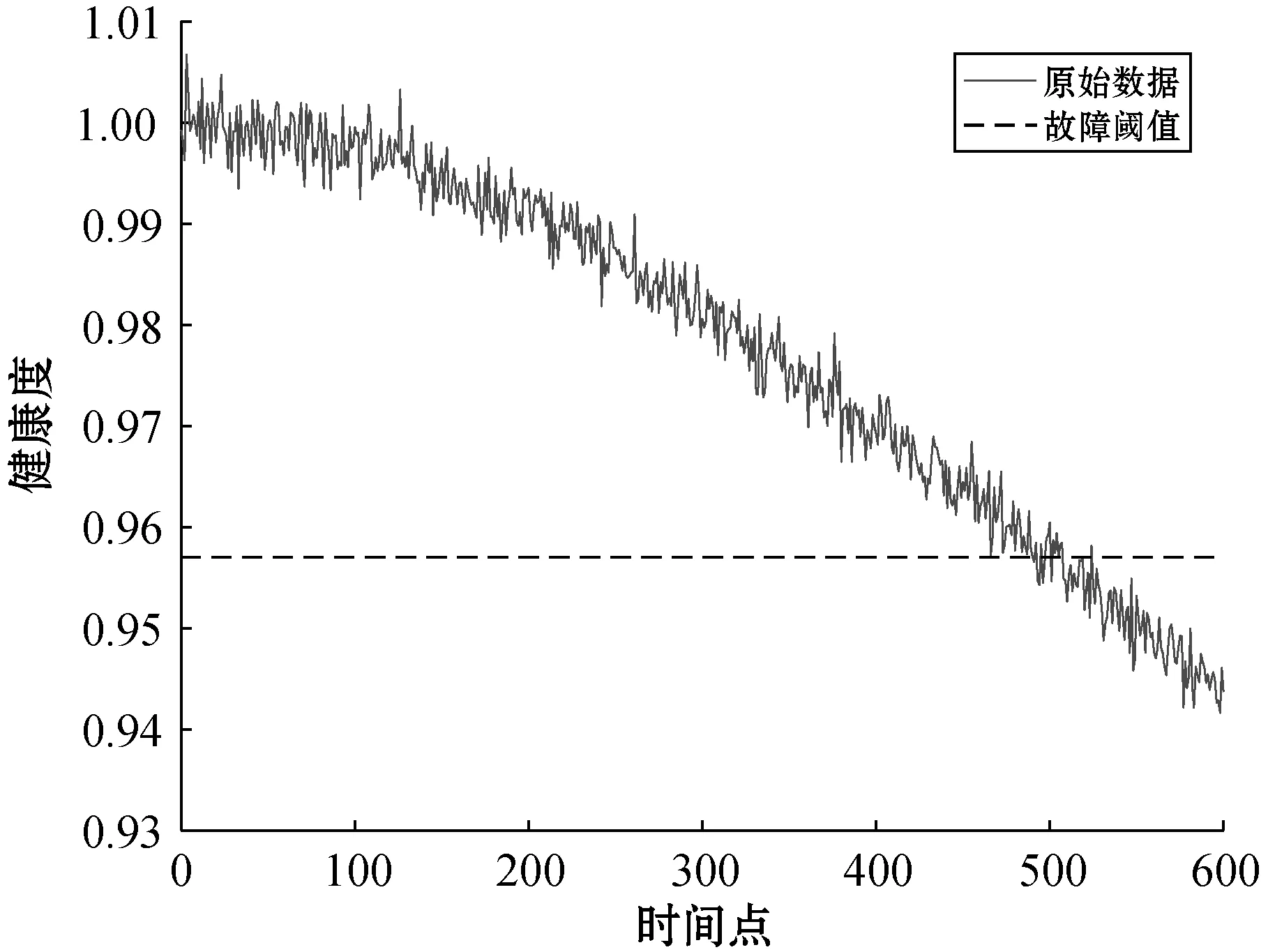
图9 添加噪声的R3健康度

假设在时间点Tnow开始预测,则RUP通过下式进行计算:

RUP=TF-Tnow

(39)

假设TEF为离散灰色多核RVM预测模型对元器件发生故障的时间点的预测值,且满足条件:

式中:H(TEF-1)为预测发生故障时间点的前一个时间点的健康度;H(TEF)为预测发生故障时间点的健康度;H(TF)为元器件发生故障时的健康度。

离散灰色多核RVM预测模型预测的RUPE为:

RUPE=TEF-Tnow

(41)

实验中R2、C1和R3分别有600组健康度随时间点变化的数据,将R2、C1和R3的前300组数据作为训练数据,后300组数据作为测试数据。首先,将训练数据输入离散灰色模型进行预测,提取预测结果更新训练数据。然后,将新的训练样本输入多核RVM回归预测模型,其中需要使用QABC算法对各个核函数的权重因子进行寻优。

在QABC算法中,蜜源数量设定为5,最大迭代次数设定为100次。在多核RVM算法中,首先采用单核RVM模型进行训练,得到较好的超参数,如表2所示。

表2 核函数的超参数

核函数的超参数设定好之后,利用训练数据对各个核函数的权重因子进行寻优操作。寻优结果如表3所示。可以看出,部分核函数对预测结果贡献较大,部分贡献较小,几乎为零。

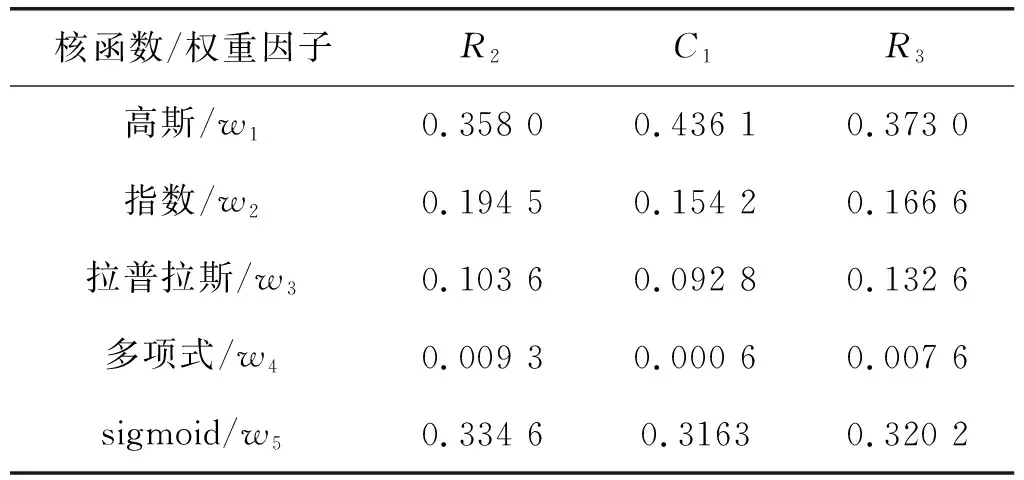
表3 应用QABC算法寻优生成的权重因子

应用表3所示的权重因子,建立离散灰色多核RVM预测模型,分别对R2、C1和R3的测试数据进行预测。预测结果的评价指标采用绝对误差(Absolute Error,AE)、相对误差(Relative Error,RE)和测试误差(Measure Error,MSE),定义如下:

EA=RUPE-RUP

(42)

式中:m为样本数据的数量;VE(i)为预测数据;V(i)为测试数据。

图10、图11和图12分别为R2、C1和R3测试数据的预测结果,各项评价指标如表4所示。

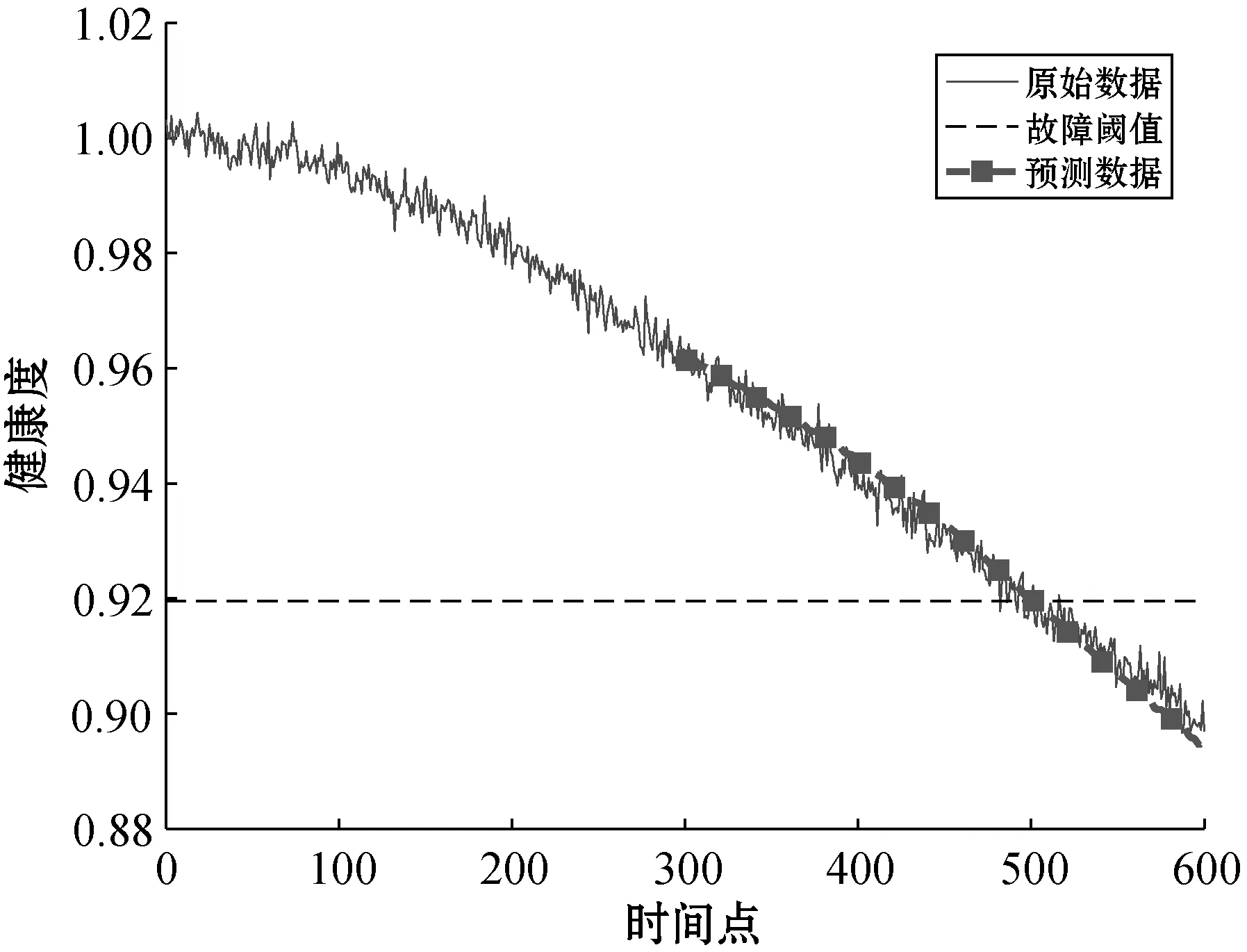
图10 基于离散灰色多核RVM预测模型的R2预测结果

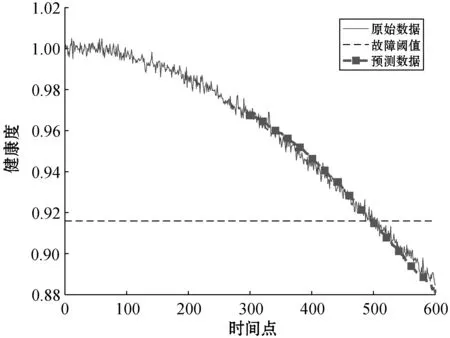
图11 基于离散灰色多核RVM预测模型的C1预测结果

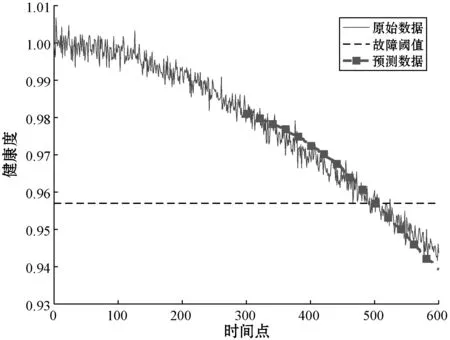
图12 基于离散灰色多核RVM预测模型的R3预测结果

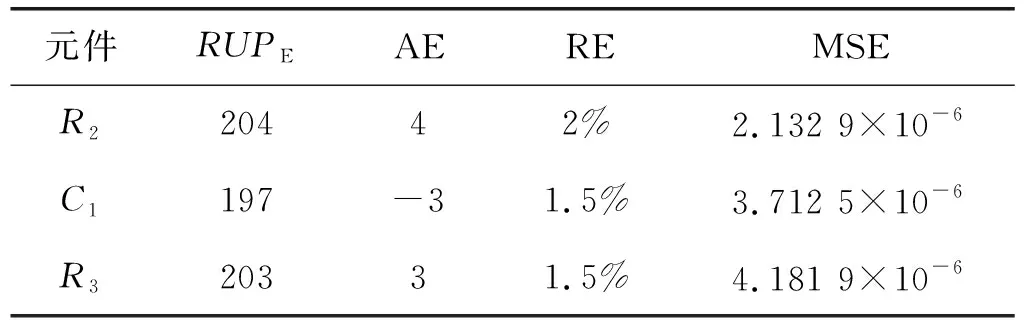
表4 基于离散灰色多核RVM预测模型的预测结果评价指标

3.3 对比实验及分析

为了进一步验证本文所提基于离散灰色多核RVM预测方法的性能,将其与传统的RVM方法进行对比,其中传统RVM中核函数选择最常用的高斯核函数,超参数设定为σ=2。训练数据和测试数据选择本次实验中的R2、C1和R3样本数据。将训练数据输入传统RVM中建立RVM预测模型,然后利用测试数据对RVM预测方法进行测试。图13、图14和图15所示分别为R2、C1和R3在基于RVM方法的预测结果,表5记录了各项评价指标。

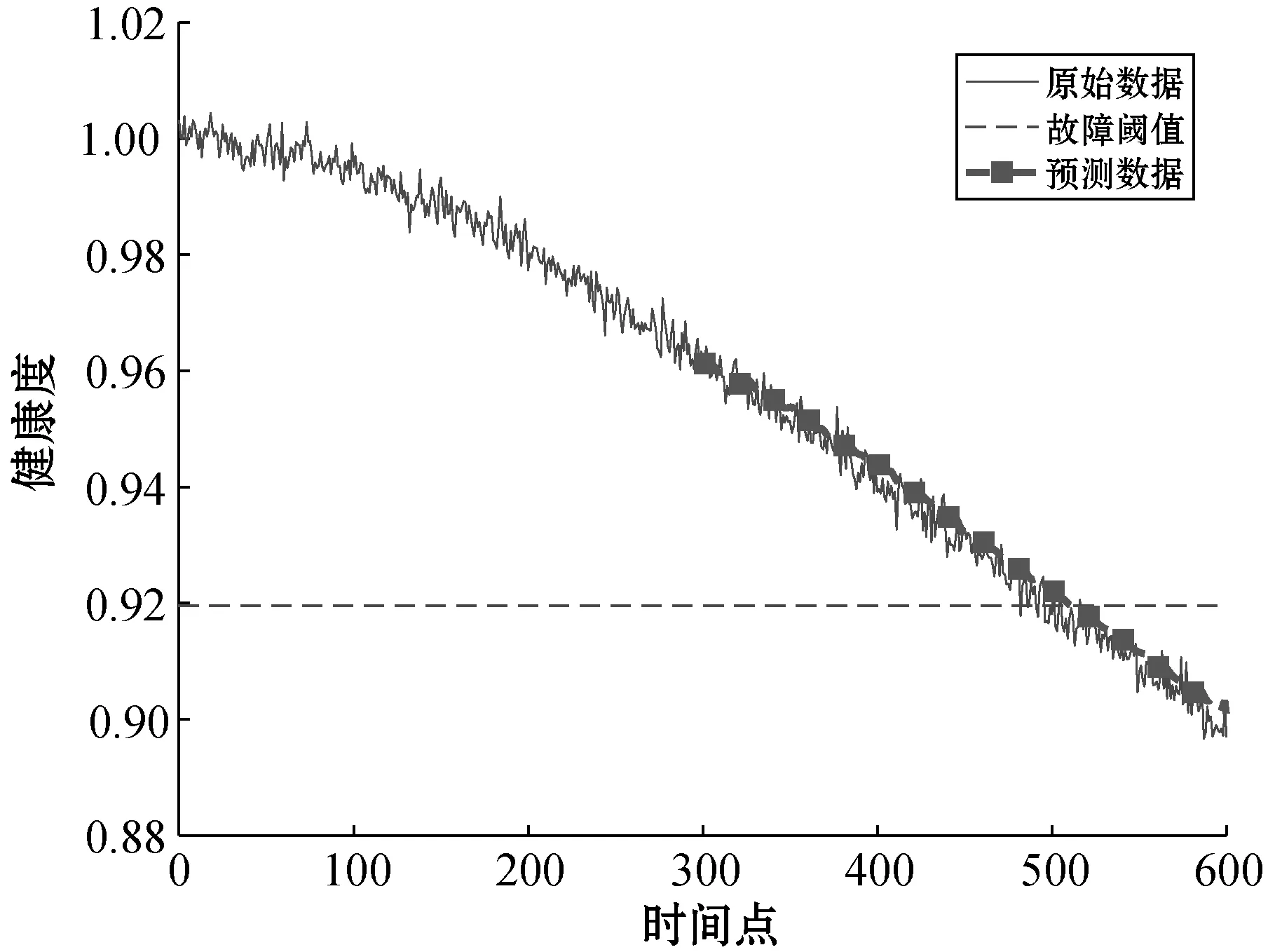
图13 基于RVM的R2预测结果

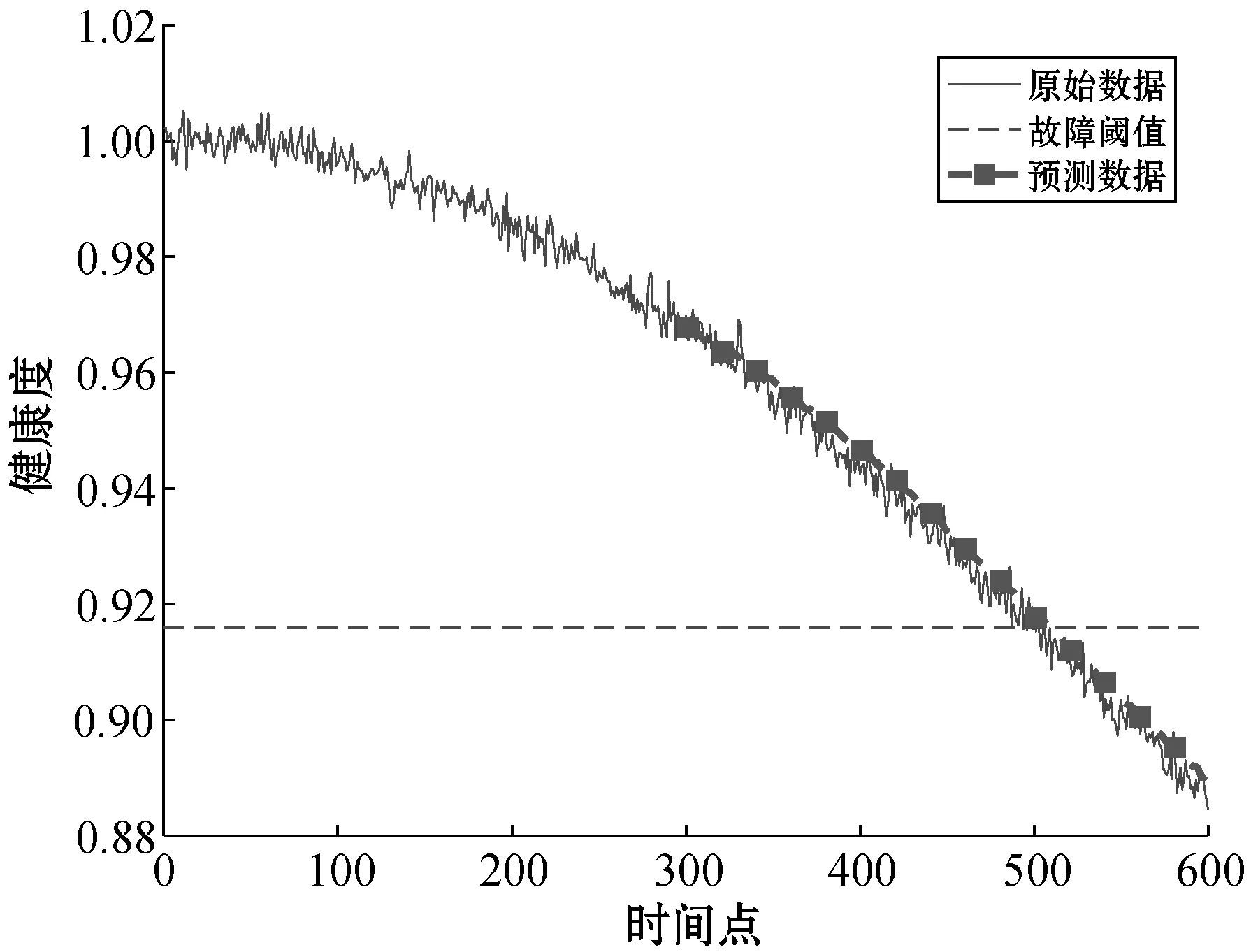
图14 基于RVM的C1预测结果

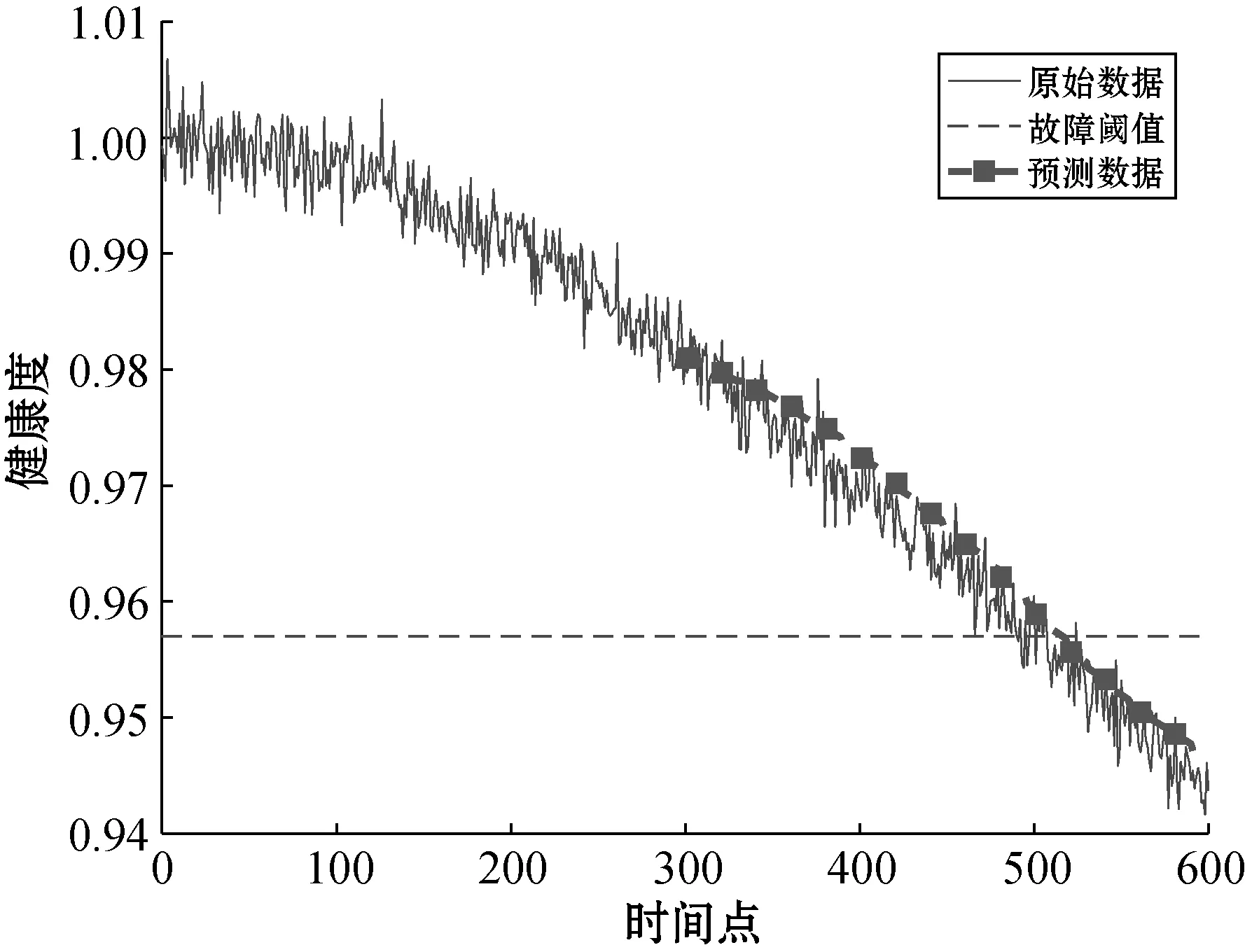
图15 基于RVM的R3预测结果

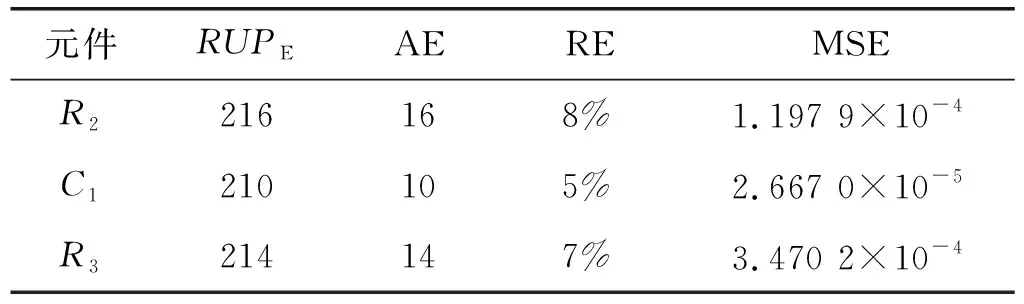
表5 基于RVM的预测结果评价指标

将本方法与当前研究中结果相对较好的量子粒子群优化多核RVM[17]方法进行对比,对比结果如表6所示。

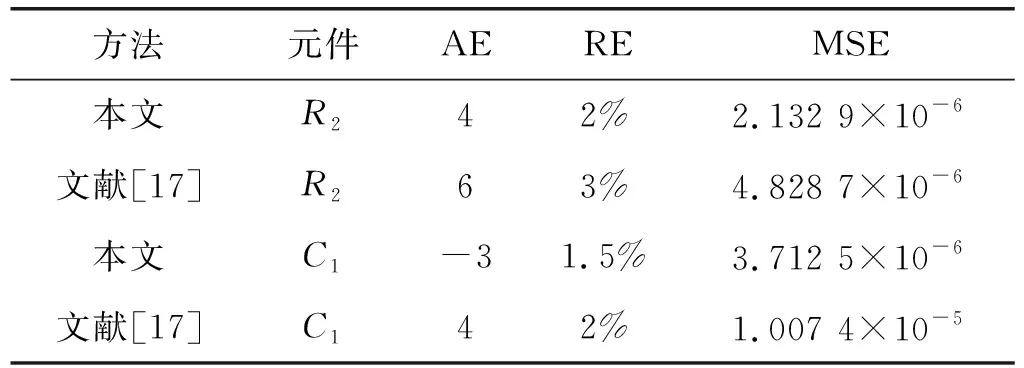
表6 对比结果

将基于离散灰色多核RVM预测方法的结果与基于RVM的预测结果进行对比,从图10、图11、图12及表4与图13、图14、图15及表5的数据可以看出,基于离散灰色多核RVM预测方法所得出的预测结果中预测数据与原始数据紧密程度更高,各项评价指标AE、RE及MSE与基于RVM的预测方法相比均有明显的提升。与量子优化多核RVM方法预测结果对比,在相同元件,样本数量相同的条件下,各项评价指标AE、RE及MSE也均有一定的提升。由对比实验可以得出结论,离散灰色多核RVM预测方法应用于模拟电路故障预测时,可以得到更好的预测效果。

4 结 语

本文提出了一种基于离散灰色多核RVM的模拟电路故障预测方法,与现有方法相比,本文方法主要的提升在于:(1) 应用简单有效的故障特征提取方法,并在样本数据中加入噪声,使样本数据更加符合实际情况;(2) 把离散灰色模型和RVM的优点相结合以及增加RVM核函数的数量及多样性,使得故障预测结果的准确性更高;(3) 利用量子方法的优势,使经过量子方法改进的人工蜂群优化算法在寻优方面取得了更好的效果。

但是模拟电路的故障预测是一个复杂问题,在现实生活中仍然面临挑战。提取的样本数据是否能准确反映实际系统的特征。建立的故障预测模型是否能对特征全部利用。这些问题都将对RUP预测的精度产生影响。下一步的研究工作将对模拟电路故障特征及预测模型进行更深入的研究以提高模拟电路故障预测精度。