圆柱壳结构水下爆炸冲击波毁伤的吸收冲量准则

2023-04-04毛致远段超伟刘刚伟胡宏伟冯海云

火炸药学报 2023年3期

毛致远，段超伟，刘刚伟，宋浦，郑监，胡宏伟，冯海云

(西安近代化学研究所，陕西西安 710065)

引言

水下爆炸是对鱼雷等目标进行硬杀伤的重要方式，主要依靠冲击波对鱼雷壳体结构造成毁伤。冲击波对目标结构的毁伤准则与判据是炸药以及水下武器战斗部威力设计与评估的重要依据[1]。圆柱壳/环肋圆柱壳作为鱼雷壳体的典型结构，国内外关于其在水下爆炸冲击波载荷下的动力学响应研究比较广泛[2-5]，但更多侧重结构响应机理的研究，较少针对炸药和武器威力设计需求来讨论爆炸威力参量对结构损伤程度的影响。在工程上常采用自由场冲击波特征参量作为准则来判定目标的毁伤程度，包括冲击波峰值压力准则、比冲量准则和能流密度准则等[6-8]。在以上单一威力参量准则的基础上，卢熹等[9]提出以Wn/L作为水下爆炸鱼雷壳体的毁伤准则，通过在不同毁伤程度时采用不同的n值，实现了不同爆炸当量时超压准则和比冲量准则的归一化。此外，也有部分学者提出了考虑结构因素的修正形式，如张文正等[10]考虑小尺寸圆柱壳的散射效应，提出以能量与散射效应修正项的乘积作为小尺寸圆柱壳的毁伤准则；姚熊亮等[11]考虑球形波在圆柱壳上的投影区域面积，提出以投射在结构上的能量作为毁伤准则。但是，冲击波与目标耦合过程还涉及传递效率问题，对于同一目标，冲量相同但衰减速率不同的冲击波，其冲量传递效率并不相同[12]，这会导致即使入射比冲量相同，有效利用冲量也并不相同，若仍以入射冲量作为衡量参数进行毁伤判别，准确度将大大降低。根据研究，冲量利用效率不仅与冲击波波形有关，还受目标特性的影响[12]。

本研究从冲量有效利用率出发，针对圆柱壳结构，建立了基于吸收冲量的毁伤准则，为对比不同工况下圆柱壳结构的毁伤程度提供了新的手段，新准则表现为冲击波峰压、衰减常数、圆柱壳几何参数以及材料密度的联合形式。结合文献数据，验证了新准则与毁伤效果的相关性，讨论了准则在对比不同工况下圆柱壳毁伤效果时的有效性和适用性。

1 理论分析

毁伤准则是指毁伤因素威力标志参量(或导出量)的类别，如冲击波峰压准则以目标处的冲击波峰值压力来评估毁伤效果，类似还有比冲量准则、能流密度准则和峰压—比冲量联合准则等[6,13-14]。在定义毁伤准则的基础上，将对目标造成一定毁伤效果的准则取值作为对应毁伤程度的判据，从而为对比不同药量、爆距乃至不同炸药类型下对应目标的毁伤程度提供依据。本节首先介绍了现有的水下爆炸冲击波毁伤准则，然后基于气背板结构的动量守恒方程，结合球面冲击波理论，计算得到圆柱壳结构在水下爆炸冲击波作用下的吸收冲量，并提出将吸收冲量作为一种新的圆柱壳结构毁伤准则。

1.1 现有的水下爆炸冲击波毁伤准则

根据水下爆炸相似律，工程计算中通常以式(1)—(3)来表示凝聚态炸药的峰压、能流密度以及比冲量对应的毁伤准则：

(1)

(2)

(3)

式中：Cp、CI和CE为分别代表冲击波峰值压力、比冲量和能流密度对应的毁伤准则；W为药量；L为爆距；Np、NI、NE是与炸药类型相关的待定系数，对于TNT，三者的取值分别为0.33、0.71、0.496[15]。对同一炸药类型，若Cp、CI或CE的取值相同，那么对应药量和爆距下的冲击波峰值压力、比冲量或能流密度就相等，从而认为目标的毁伤程度相等[6]。

1.2 圆柱壳结构吸收冲量准则CI_cylinder的理论推导

1.2.1 气背板微元的冲量传递比计算

不同于平板结构，圆柱壳表面为曲面，因此针对平板结构的吸收冲量计算方法不再适用，但从微观角度看，圆柱壳表面每一微元仍近似为平面结构，因此可对微元进行计算，再积分得到圆柱壳结构总吸收冲量。

水下爆炸冲击波压力时间曲线可以表示为p=pme-t/θ，其中pm为峰值压力，θ为冲击波衰减常数，t为时间变量。基于Taylor平板模型，假设水是不可压缩理想流体，忽略透射波及边界的影响，可对气背板微元建立如下控制方程[16]：

(4)

式中：up为板的运动速度；m为单位面积板的质量；ρw为水的密度；cw为水中声速。

求解式(4)可以得到最大速度为：

(5)

其中β=ρwcwθ/m。速度最大时获得的动量代表了微元在壁压正压段的比冲量，从而每单位面积获得的比冲量为Ip=mum，而自由场水下爆炸中理论入射冲击波的总冲量为：

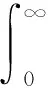
(6)

定义冲量传递比为ζ=Ip/Im，则由式(5)和(6)可得气背板结构的冲量传递比为：

ζ=ββ/(1-β)

(7)

1.2.2 圆柱壳结构吸收总冲量的计算

圆柱壳表面为曲面，且实际爆炸时冲击波以球面波形式传播，因此除迎爆面中心点外，其余壳结构表面微元处的冲击波均不是正入射，需要根据实际入射情形进行修正，以避免过大的计算误差。

在壳体迎爆面上任取一点，该点冲击波的入射方向如图1所示。

图1 冲击波斜入射示意图Fig.1 Schematic diagram of oblique incidence of shock wave

此时实际入射爆距为：

(8)

由水下爆炸相似律可得A点的峰值压力为：

(9)

式中：kp和αp为对应炸药的水下爆炸冲击波峰压相似律系数；W为装药质量。从而由几何关系可得，平行于圆柱壳A点法线O1A的压力分量为：

pm_A_normal=pm_A·cosα

(10)

其中

(11)

类似的，依据水下爆炸相似律可得A点对应的冲击波时间常数为：

(12)

式中：kθ和αθ为对应炸药的水下爆炸冲击波衰减常数相似律系数。将式(12)代入式(7)可得A点处对应的冲量传递比ζA，再结合式(6)可得在A点处，圆柱壳结构每单位面积平均获得冲量为：

(13)

其中βA=ρwcqθA/m，IA_normal为A点处入射冲击波在平行于圆柱壳法线方向的冲量分量。将式(13)得到的IA_plate在圆柱壳迎爆面进行积分就可以得到总的实际获得冲量：

Icylinder=∬SIA_platedS

(14)

其中迎爆面区域S的范围受爆距与圆柱壳半径比值的影响，示意图见图2。

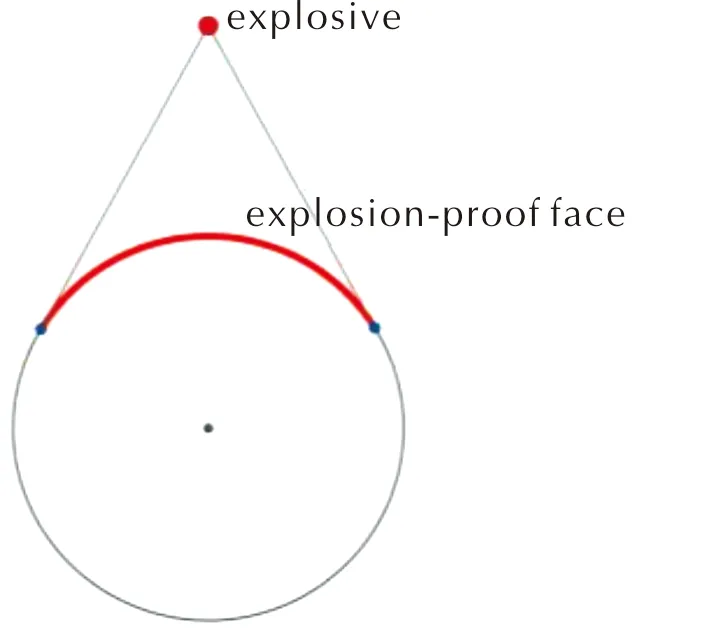
图2 迎爆面区域示意图Fig.2 Schematic diagram of explosion-proof face

从图2可以看到，随着爆距与圆柱壳半径比值变化，迎爆面区域随之变化。

1.2.3 吸收冲量准则CI_cylinder的定义

基于上述计算过程，可以定义一个圆柱壳结构在水下爆炸冲击波作用下的新毁伤准则CI_cylinder，它表征了圆柱壳结构在与冲击波耦合过程中实际获得的总冲量，吸收冲量准则CI_cylinder的定义式为：

(15)

式中：pm_A_normal由式(10)和(11)得到；θA由式(12)得到；βA=ρwcwθA/m；S代表圆柱壳迎爆面。

上述表达式在计算上存在一定难度，为便于工程应用，以下列出一种无需积分计算的简化方法。设迎爆面上距离爆心最近的一点为N点，则这一点与爆心的距离为L，设目标圆柱壳半径与爆距L的无量纲比值为RL=R/L，圆柱壳长度与爆距L的无量纲比值为HL=H/L，其中H表示圆柱壳受载区域的长度，从而可以用N点的单位面积吸收冲量乘以结构尺寸修正项的形式来近似计算准则的取值：

(16)

其中

(17)

式中：H为圆柱壳受载区域长度；f为结构尺寸修正项，是在对定义式进行变量分离和无量纲化的基础上，对原积分式进行泰勒级数拟合得到的近似计算式。

吸收冲量准则CI_cylinder考虑圆柱壳结构与球面冲击波的耦合过程，以圆柱壳实际获得冲量为物理含义，以冲击波峰压、时间常数、圆柱壳几何参数以及材料密度的组合为表现形式，为对比和评估鱼雷壳体在不同爆炸载荷作用下的毁伤效果提供了新的依据。

2 验证与分析

2.1 吸收冲量准则CI_cylinder的有效性验证

文献[17-18]针对圆柱壳结构进行了多次水下爆炸试验，并建立了对应的仿真模型。通过改变药量与爆距，得到了多组不同工况冲击波作用下迎爆面中心点的变形挠度。上述研究中，圆柱壳半径(R)为100mm，长(H)为185mm，壁厚2.8mm，材料为AL7075，材料密度为2804kg/m3。圆柱壳内部均布两根环形肋，两端连接等外径钢制配重，圆柱壳整体结构如图3所示。依据试验工况建立的仿真模型如图4所示，药球正对圆柱壳侧面中心位置，定义圆柱壳迎爆面中心点到药球中心点距离为爆距L。

图3 圆柱壳结构图Fig.3 Structural diagram of cylindrical shell

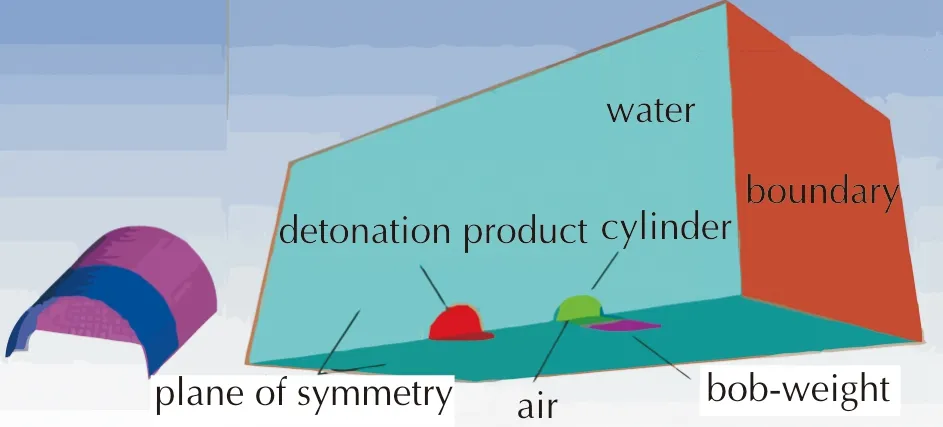
图4 仿真模型Fig.4 Simulation model

通过改变装药的质量W与爆距L，文献[18]中仿真计算并分析了圆柱壳的变形模式，得到了不同工况下圆柱壳迎爆面中心点的变形挠度ω，对应关系如图5所示，图中分别选取10、50、100、200、400、800g药量进行了多次仿真计算。

图5 不同药量下变形挠度随爆距的变化曲线Fig.5 Variation curve of deformation deflection with explosion distance under different charge quantities

结合文献[18]中的分析，加筋圆柱壳的变形模式分为迎爆面整体塌陷变形和局部凹陷变形两种子模式，而在不同的变形模式下，毁伤准则将不再适用。从文献中的分析可知，整体塌陷变形出现在大部分的工况中，是圆柱壳的主要损伤模式；局部凹陷变形仅在少量小爆距工况下出现，因此在下文的分析中，剔除了爆距小于0.25m的工况。需要说明的是，文献中采用的是环肋圆柱壳，由于肋骨面积仅占圆柱壳总面积的4%，因此下文在计算吸收冲量时忽略了加筋肋的影响，近似视作均匀壳结构。

1.2.3节中为吸收冲量准则CI_cylinder提供了两种计算方法，分别是式(15)中的直接积分方法以及式(16)和(17)中的简化计算方法。首先对两种方法计算得到的准则取值进行对比，图6中计算了所有工况下两种计算方法的相对误差。

图6 不同工况下两种计算方法的相对误差Fig.6 Relative error of two calculation methods in different working conditions

从图6中可以看到，两种计算方法得到的结果基本一致。对于全部48个工况，两种准则计算方法之间的相对误差最大仅为0.9%以内，因此可以认为，简化后的计算方法可以准确地对准则CI_cylinder的取值进行计算。

结合图5中的工况参数，计算得到变形挠度随几种毁伤准则参数的变化曲线如图7所示，其中冲击波峰压准则、能流密度准则与比冲量准则由式(1)-(3)计算得到，吸收冲量准则由式(16)和(17)计算得到。

图7 不同毁伤准则下挠度随准则取值的变化曲线Fig.7 Variation curves of deflection with the value of criterion under different damage criteria

从图7(a)-(c)中可以看到，冲击波峰压准则、能流密度准则与比冲量准则下，对应于相同药量，准则取值越大则挠度越大。而在不同药量之间，上述三个准则的取值均不能准确反映变形挠度的大小，相同的毁伤准则取值下，药量不同，毁伤效果存在明显差异，其中以比冲量准则差异最为显著，这就使得利用这三个毁伤准则取值来对比不同工况的毁伤程度时缺乏准确性。好的毁伤准则，其取值应当与毁伤程度具有强的单调对应关系，结合图7可以看到，峰压准则CP和比冲量准则CI均不能较好地表征不同药量下的毁伤效果，而能流密度准则CE和吸收冲量准则CI_cylinder则可以进行相对有效的表征，其中吸收冲量准则CI_cylinder的效果更优。

为了定量对比能流密度准则CE和吸收冲量准则CI_cylinder，以下将两个准则分别与变形挠度进行回归拟合。观察图7(c)和(d)中数据点的变化趋势，整体表现为单调上升，且上升程度逐渐增大，不失一般性，选取三次多项式函数进行拟合。将以上两个准则的拟合曲线进行绘制，结果见图8。

图8 两种准则与变形挠度拟合结果Fig.8 Fitting results of two types of criteria and deformation deflection

从图8可以直观地看到，CI_cylinder的取值与变形挠度的相关性更强，散点图更集中的分布在拟合曲线周围；而CE的拟合曲线图中，在挠度逐渐上升时散点图趋于分散。从均方误差来看，能流密度准则CE和吸收冲量准则CI_cylinder分别为0.68和0.16，后者比前者降低了76%；从拟合R2来看，能流密度准则CE的R2为0.930，吸收冲量准则CI_cylinder对应的R2为0.983，一般认为，R2大于0.9时相关性显著，在此基础上越接近1相关性越强，等于1时完全相关，因此可以说明，吸收冲量准则CI_cylinder与变形挠度之间具有更强的相关性，可以更有效地表征圆柱壳结构的毁伤效果。

2.2 准则CI_cylinder的适用性分析

基于以上分析，采用峰压、比冲量和能流密度得到的毁伤准则在对比毁伤效果时受药量影响较大，不同药量时，即使准则取值相同，毁伤效果也有较大差异，与之相比，吸收冲量准则CI_cylinder的一致性较好，与变形挠度的相关性显著高于其他几种准则，能更准确表征不同工况下圆柱壳的毁伤效果。此外，在2.4节所提出的简化计算方法有效避免了积分计算的困难，并且能准确的逼近积分计算方法的结果。鉴于文献[18]中实际采用的是环肋圆柱壳，因此可以进一步说明，对于鱼雷壳体等简单的环肋结构，将其近似看作均匀壳体来计算结构的吸收冲量进而确定准则CI_cylinder的取值是可取的。

需要注意的是，毁伤准则仅在结构变形模式为整体变形时有效，此时准则取值与变形挠度保持强单调相关性，当圆柱壳结构以局部变形模式为主时，准则不再适用。结合文献[18]的分析，局部凹陷变形可能是由于爆距较近时波阵面曲率较大导致的，就本研究所采用的算例，当半径与爆距L之比RL>0.4时准则便不再适用，此时可能更适宜采用比冲量、峰压等作为判断准则。如何准确判定不同圆柱壳结构的变形模式，以及如何修正文中所提准则，使之适用于局部凹陷变形模式，需要进一步研究。

基于本研究结果可以合理推测，若对积分曲面进行替换，准则CI_cylinder将能适用于更丰富的曲面壳体结构，如锥柱壳结构、椭球壳结构等。此外，吸收冲量准则CI_cylinder在传统准则考虑药量和爆距参量的基础上，进一步考虑了结构尺度以及密度参量，或可用于对缩比模型和实体之间的毁伤效果进行比较和转换。