火炸药静电感度试验数理统计方法分析与优化
2023-04-04孙铭泽王艳平罗太明饶云鹏张腾月
孙铭泽,王艳平,罗太明,饶云鹏,张腾月,曾 丹
(1.中国兵器工业火炸药工程与安全技术研究院, 北京 100053;2.中国兵器科学研究院, 北京 100089)
引 言
静电放电一直是火炸药安全生产领域重点关注的安全风险因素之一,其放电火花可引起火炸药燃烧或爆炸,继而对火炸药生产、储运等过程造成潜在风险和重大安全隐患[1-5]。因此,火炸药的静电感度,或者静电放电引燃的最小能量(Emin),是表征火炸药安全性能的重要参数之一。
由于静电放电最小引燃能量(Emin)难以直接且准确地测量,加之环境因素影响具有随机性和偶然性,故当前火炸药的静电安全特性主要通过静电感度来表征,即火炸药在静电放电火花的作用下,发生燃烧或爆炸的难易程度[2,4]。
当前,静电感度试验主要基于数理统计方法设定试验程序,开展系列静电发火试验,计算得到静电放电能量与火炸药响应概率的关系[7-12]。现行火炸药静电感度试验标准[13-17]都采用升降法设定试验程序,准确度较差,只能得到被试样品50%响应概率所对应的静电放电能量(E50),不能准确测算极小概率(如百万分之一)响应点,一定程度上影响了火炸药静电安全风险评估的准确性和有效性。
除升降法外,典型的感度试验数理统计方法还包括兰利法和最优化D法。兰利法是一种变步长的升降法[9],被应用于部分炸药短脉冲起爆感度试验方法和标准中,可快速得到50%概率感度数据;最优化D法属于最优化方法[7-8],操作和计算流程较为复杂,但试验准确性较高,已被应用于美国感度试验军用标准。但因缺少相关研究验证,兰利法和最优化D法均未被应用于国内的火炸药静电感度试验方法和标准之中。
因此,亟需开展基于不同数理统计方法的静电感度试验准确性研究,优选或改进现有数理统计方法,在最少试验次数内,获得更准确地火炸药静电感度分布,以提高对百万分之一概率发火能量(E1ppm)等极小概率响应点的测算准确性,也能更准确地估计Emin等火炸药安全性能参数。
本研究利用蒙特卡罗方法进行计算机模拟试验对比,分析基于典型数理统计方法进行静电感度试验的特点,并对现有的兰利法进行优化和改进,开展升降法、兰利法、最优化D法以及优化和改进后的兰利法4种方法的准确性研究,以期为优化火炸药静电感度试验方法和标准提供理论依据,也为获得更准确的火炸药静电最低引燃能量提供方法和途径。
1 典型数理统计方法及对比分析
国内现行的感度试验数理统计方法标准[18]中推荐了升降法和兰利法等方法,美国军用标准 MIL-DTL-23659D于2013年将最优化D法作为火炸药感度试验数理统计方法。因此,升降法、兰利法和最优化D法都是目前国内外最具代表性的感度试验方法,本研究将对这3种典型数理统计方法展开研究分析。
1.1 升降法
升降法最早由 W. J. Dixon 和 A. M. Mood 在1948年提出[5,10,12,19],其流程简单,是国内最常用的火炸药静电感度试验数理统计方法。GJB/Z 377A-94对升降法的数据处理给出的均值计算公式为:
(1)
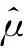
(2)
(3)
(4)
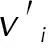

1.2 兰利法
兰利法由H. J. Langlie于1963年提出,并由Guillaume 在2010年补充了操作细节[20],是一种变步长升降法,可快速得到50%概率感度数据,具有可操作性高的特点,试验前只需提供全不响应刺激量xL作为试验下限、全响应刺激量xU作为试验上限,每次试验点的计算只涉及简单的四则运算。首次试验时选择上下限平均值作为初始静电刺激量x0,随着试验次数增加,测点集中在感度分布均值处,可快速收敛获得静电感度分布均值,但不能准确测算分布方差,继而影响了如E1ppm等依赖于方差的极小概率静电引燃能量的测算准确性。
1.3 最优化D法
最优化D法是由Barry T. Neyer在1994年提出的一种基于Fisher信息矩阵的静电感度试验数理统计方法[7,8,21,22],每次试验前需先计算静电感度分布,然后优化新的刺激量,使试验后静电感度分布的整体测算误差最小,但每次试验需要求解复杂的非线性优化问题,程序设定和计算十分复杂,操作难度大。此外,最优化D法需在预试验后进行,Barry T. Neyer 最初提出的方法被称为Neyer-D法,基于折半查找法进行预试验[22]。华东师范大学的吴蔚[23]对其进行改进提出兰利-最优化D法,可同时获得较为准确的感度分布均值和方差,并对E1ppm等极小概率静电引燃能量进行准确度较高的测算。因此,本研究选择兰利-最优化D法作为最优化D法的代表。
基于最优化D法进行静电感度试验时,若试验次数较少时,则会因样本不足以覆盖极端情况而使测算的方差整体偏小,可通过引入大于1的偏量修正因子提高方差测算的准确性:
σC=β×σ
(5)
式中:β为修正因子,是试验次数N的函数;σ为修正前方差;σc为修正后方差。本研究基于最优化D法开展不同次数的模拟试验,计算得到静电感度分布方差与设定真值之比作为偏量修正因子βi:
(6)
式中:Ni为模拟试验次数;βi为Ni次模拟试验对应的偏量修正因子;σi为Ni次模拟试验后静电感度分布方差测算值;σ0为静电感度分布方差设定真值。将试验次数Ni与对应的偏量修正因子与组合为数据对(Ni,βi),并基于最小二乘法拟合得到最优化D法的偏量修正因子β与试验次数N之间的数学表达式。
本研究分别基于修正前后的最优化D法进行不同次数的模拟试验,不仅能验证修正因子的有效性,也能分析基于该方法开展静电感度试验的特性。
2 兰利法的优化和改进
针对兰利法方差测算准确性不高的问题,本研究突破了原有方法测点集中在50%概率响应点附近的模式,探索性地提出将测点分散在30%概率和70%概率响应点周围,以寻找被测样品静电感度分布的离散程度,从而更准确地捕捉分布方差。
基于改进的兰利法开展静电感度试验的具体做法如下:
(1)试验前设定全不响应刺激量xL作为试验下限、全响应刺激量xU作为试验上限,首次试验选择试验上下限的算数平均值作为测点刺激量;
(2)在计算出的刺激量下进行静电感度试验,记录第i次试验的刺激量xi和响应vi后,从本次试验开始往前查找历史试验记录。
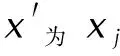
(4)若查找到j=1仍未满足要求,则当vi=1时取定中间变量为xL,反之vi=0则取定中间变量为xU。
(6)重复步骤(2)~(5),直至试验次数满足设定要求后,基于最大似然法计算静电感度分布均值和方差以及不同响应概率临界刺激量等结果。
当试验次数足够多时,符合条件的xj会接近样品50%概率响应点,而中间变量取为其和试验上限或下限的均值,则可有效地将测点分散在较小或较大概率响应点周围,可比传统兰利法更准确地测算静电感度方差。同时,改进后的兰利法虽然操作上略复杂于原方法,但其每次测点建议值依然可通过简单的四则运算得到,计算复杂度远低于最优化D法。
基于改进的兰利法进行静电感度试验时,也可根据(5)式和(6)式引入偏量修正因子减小方差的测算误差。本研究通过模拟试验,拟合得到改进兰利法的偏量修正因子,并分别基于修正前后的改进兰利法进行不同次数的模拟试验,不仅能验证修正因子的有效性,也能分析基于该方法开展静电感度试验的特性。
3 蒙特卡罗试验研究方法与流程
蒙特卡罗方法是一种对随机过程进行模拟后统计结果的计算机模拟试验方法。本研究将通过蒙特卡罗法开展计算机数值模拟试验,分析基于升降法、兰利法、最优化D法、改进的兰利法4种不同数理统计方法获得结果的准确性,具体研究方法如下:
(1)设定初始刺激量x0=μ,步长d=σ,分别基于勘误前后的升降法进行模拟试验,对比勘误前后结果的准确性;分别设定d=σ和d=σ/2进行模拟试验,分析不同步长对升降法准确性的影响。
(2)设定试验上下限为[xU,xL]=[μ+3σ,μ-3σ],基于兰利法进行不同次数的模拟试验。
(3)基于最优化D法进行模拟试验,拟合偏量修正因子;设定试验上下限为[μ+3σ,μ-3σ],对比有无偏量修正因子时,基于最优化D法进行模拟试验的准确性;分别设定试验上下限为[μ-3σ,μ+3σ]和[μ-2σ,μ+σ]两种情况,基于最优化D法进行模拟试验,对比分析试验上下限对其准确性的影响。
(4)基于优化和改进后的兰利法进行模拟试验,拟合偏量修正因子;设定试验上下限为[μ+3σ,μ-3σ],对比有无偏量修正因子时,基于改进的兰利法进行模拟试验的准确性;分别设定试验上下限为[μ-3σ,μ+3σ] 和[μ-2σ,μ+σ]两种情况,基于改进的兰利法进行模拟试验,对比分析试验上下限对其准确性的影响。
(5)对比分析基于上述4种方法开展模拟试验的测点选择的有效性,静电感度分布均值和方差的测算准确性,以及小概率响应点的测算准确性。
上述研究内容中开展模拟试验的具体流程如下:
(1)设定静电感度分布的真值,将其设为均值μ0=10,方差σ0=1的正态分布;
(2)按方法计算每次试验的测点刺激量xi,并基于静电感度分布真值计算响应概率,并生成试验结果vi;
(3)设定模拟试验的次数N,完成一组N次试验后,根据测点刺激量x1,x2,…,xN和响应情况v1,v2,…,vN,基于所选方法计算静电感度分布均值和方差的测算值μα、σα,其中α=1,2,...标记不同组模拟试验;
(4)基于测算出的均值和方差计算1%、0.01%、10-4%等小概率响应点临界刺激量:
xα(p)=μα+upσα
(7)
式中:μα、σα为第α组模拟试验得到的静电感度分布均值和方差;xα(p)为概率p响应点静电临界刺激量;up为概率p对应的标准配位数,例如u1%≈-2.33,u1ppm≈-4.75;
(5)重复步骤(2)~(4)进行M组模拟试验后,统计分析静电感度分布测算值与真值之间误差的均值与标准差:
ΔXα=Xα-X0
(8)
(9)
(10)
式中:Xα为第α组模拟试验测算结果(可为感度均值、方差或小概率响应点);X0为对应设定真值;ΔXα为第α组模拟试验测算误差;ME(ΔXα)为第α组模拟试验测算误差均值;SD(ΔXα)为第α组模拟试验测算误差标准差;M为模拟试验组数;
(6)计算模拟试验测算结果误差在约68.26%置信度(单σ)下的置信区间,并绘制误差线图:
ΔXU=ME(ΔX)+Z(1-p)/2SD(ΔX)
(11)
ΔXD=ME(ΔX)+Z(1-p)/2SD(ΔX)
(12)
式中:p为置信度;ΔXU为置信区间上限;XD为置信区间下限;ME(ΔX)为结果X误差的均值;SD(ΔX)为结果X误差的标准差;;Z为正态分布标准分数,为计算方便本研究将其取1对应约68.26%的置信度。
当静电感度分布均值和方差测算误差的均值和标准差相对较小时,小概率响应点临界刺激量测算误差的均值和标准差可由其计算得到:
ME[Δx(p)]=ME(Δμ)+upME(Δσ)
(13)
SD[Δx(p)]=SD(Δμ)+upSD(Δσ)
(14)
式中:μ、σ、x(p)和up的定义同式(7);ME为其均值;SD为其标准差。因此,本研究在通过数值模拟试验分析4种方法特点时只分析了静电感度均值和方差。
试验中需令M≫N(将M取为100×N),使单组模拟试验不确定性带来的误差降低到可忽略,保证统计的有效性。此外,取不同的试验次数N进行模拟试验,研究试验次数对结果准确性的影响,并将最大试验次数取为1000。蒙特卡罗计算机模拟试验的具体技术途径如图1所示。
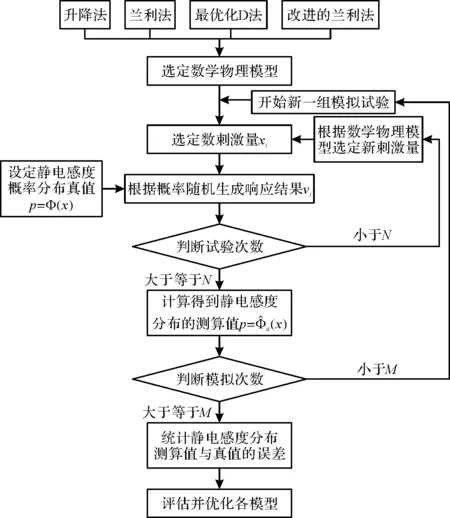
图1 蒙特卡罗计算机模拟试验流程图Fig.1 Flow chart of Monte Carlo computer simulation test
4 结果对比与准确性分析
针对升降法、兰利法、最优化D法和改进的兰利法进行蒙特卡罗模拟试验的结果进行对比分析,具体见图2。
4.1 升降法
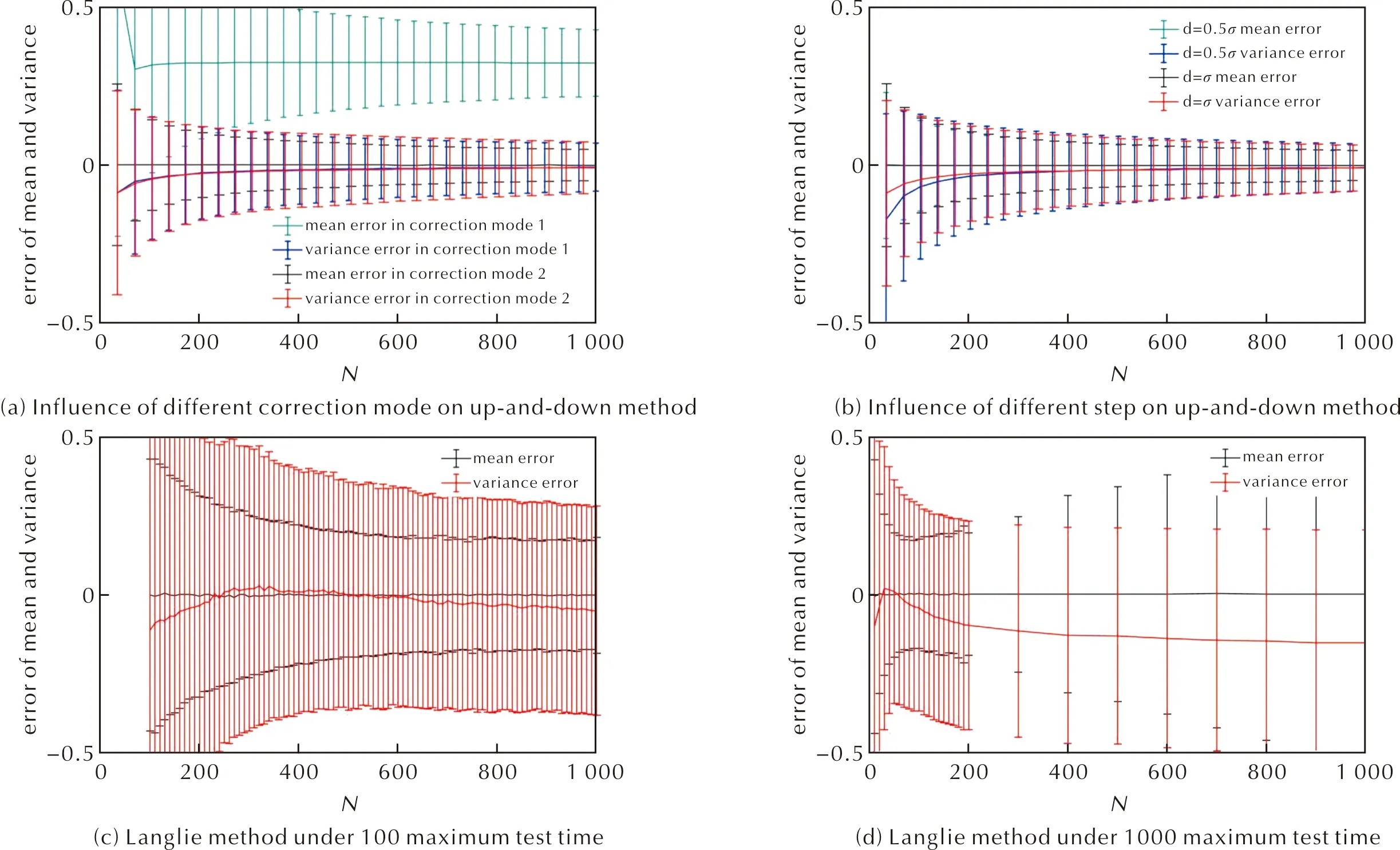
模拟试验结果显示,按照前文1.1中介绍的勘误模式1的升降法进行模拟试验,当试验次数达1000次时,绝对误差的统计平均值仍有约+0.32;而经前文1.1中勘误模式2的升降法对静电感度分布均值和方差的测算都较准确,误差统计平均值几乎为0,且测算误差随试验次数增加而降低,如图2(a)所示,图2和图3中的所有子图均以误差线的形式展现测算误差,因此,本研究采用模式2对GJB/Z 377A-94中介绍的升降法勘误;此外,当步长设定为静电感度分布方差真值时,升降法的准确性尚可,但当步长设定偏离方差真值时,其在试验次数较少时,对方差的测算误差显著增大,如图2(b)所示。
因此,基于升降法进行试验可对静电感度分布的均值有效测算,得到较准确的50%响应点,但对方差测算误差较大,所以无法获得准确的极小概率响应点;而且升降法测试结果的准确性依赖于初始步长设定,稳定性较低。
4.2 兰利法
模拟试验结果显示,基于兰利法进行静电感度试验时,在约40次试验内可以快速获得较准确的静电感度分布均值;但随着试验次数增加,试验中的静电刺激量会聚集在测算出的50%概率静电响应点处,无法获取其他响应点信息,导致测算误差随试验次数增加反而增大,如图2(c)和(d)所示。此外,兰利法和升降法类似,只对静电感度分布均值测算较准,而对方差的测算误差较大。
4.3 最优化D法
根据模拟试验结果,可拟合最优化D法偏量修正因子表达式:
(15)
式中:β为修正因子;N为试验次数;a为拟合参数。模拟试验结果显示,基于最优化D法进行静电感度试验可同时准确获得其分布均值和方差,且偏量修正因子会显著降低100次试验以内的方差的测算误差,如图2(e)所示,只有100次试验内修正前后的感度分布方差测算误差有所区别,其他上下限条件下的结果几乎在图像上重合,如图2(f)所示,说明上下限取值对最优化D法获得的静电感度分布测算误差无明显影响。
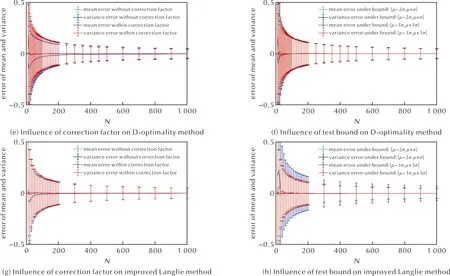
图2 四种数理统计方法在不同情况下试验结果测算误差对比Fig.2 Comparison of the test result error under different conditions by four different mathematical statistical methods
因此,引入偏量修正因子后,最优化D法对静电感度分布的均值和方差可同时准确测算,且结果准确性不依赖于试验上下限的选取,稳定性较高。
4.4 改进的兰利法
根据模拟试验结果,可拟合改进的兰利法偏量修正因子表达式:
(16)
式中:β为修正因子;N为试验次数;a,b为拟合参数。模拟试验结果显示,基于改进的兰利法进行静电感度试验,也可同时准确地测算分布均值和方差,修正因子可有效改善100次试验内方差测算的整体偏差,如图2(g)所示,只有100次试验内修正前后的感度分布方差测算误差有所区别,其他情况下修正前后的数据线在图中重合。此外,上下限选择会影响改进兰利法的测算结果,特别是方差测算结果准确性,但其稳定性依然优于原始的兰利法,如图2(h)所示。
因此,引入偏量修正因子后,改进的兰利法可凭借远低于最优化D法的操作难度和计算复杂度,对静电感度分布均值和方差同时进行准确测算,只是稳定性略差于最优化D法。
4.5 方法准确性对比与分析
首先,对比4种不同方法试验的测点分布:升降法测点集中在静电感度分布均值及其两侧;兰利法测点聚集在均值附近;最优化D法的测点分散在约15%和约85%概率响应点两处;而改进的兰利法测点均匀地分散在约30%概率和约70%概率响应点周围,如图3(a)所示。
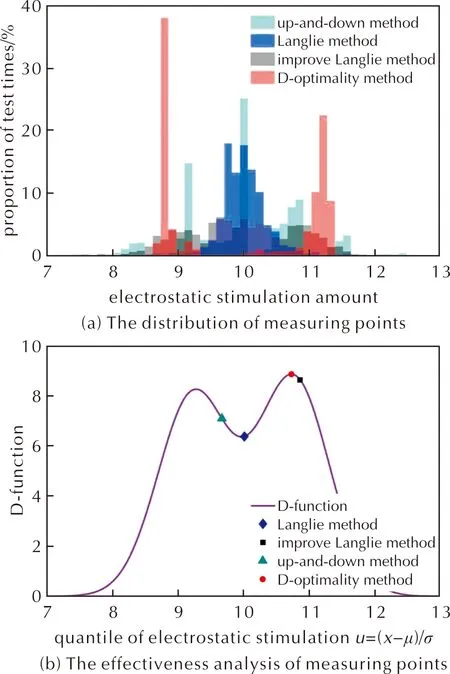
图3 不同数理统计方法测点对比分析Fig.3 Comparison and analysis of measuring points with different mathematical statistics methods
利用Fisher信息矩阵的行列式,即D函数,可评估试验中测点选择的有效性。在测点位置进行一次新的试验后,静电感度分布测算误差矩阵的行列式等于D函数的倒数,可反映测点对静电感度分布准确测算的有效贡献。结果显示,从兰利法、升降法、改进的兰利法到最优化D法,D函数递增,测点选择有效性依次增加,如图3(b)所示。
其次,对比不同方法对静电感度分布均值与方差的测算误差。结果显示,与均值为10和方差为1的设定真值比较,升降法、最优化D法和改进的兰利法对静电感度分布的测算误差均随试验次数增加而降低;升降法对均值的测算误差尚可,但对方差的测算误差最大;兰利法能快速测算出较准确的均值,但试验次数增多后测算误差反而增大;优化和改进的兰利法对均值与方差的测算误差均尚可;最优化D法表现最佳,对均值和方差的测算误差均最小,如图4(a)和(b)所示。

图4 不同数理统计方法均值和方差误差对比Fig.4 Comparison of measurement errors of mean and variance by different mathematical statistics methods
仅从均值和方差的测算上考虑,优化和改进后的兰利法和最优化D法的准确性难分伯仲。因此,进一步分析其对小概率响应点的测算准确性,与百万分之一、万分之一和百分之一3个小概率响应点的设定真值(约5.245、6.28、7.67)比较,各方法的测算误差如图5所示,典型试验次数下百万分之一概率响应点的测算结果的测算误差对比如表1所示。
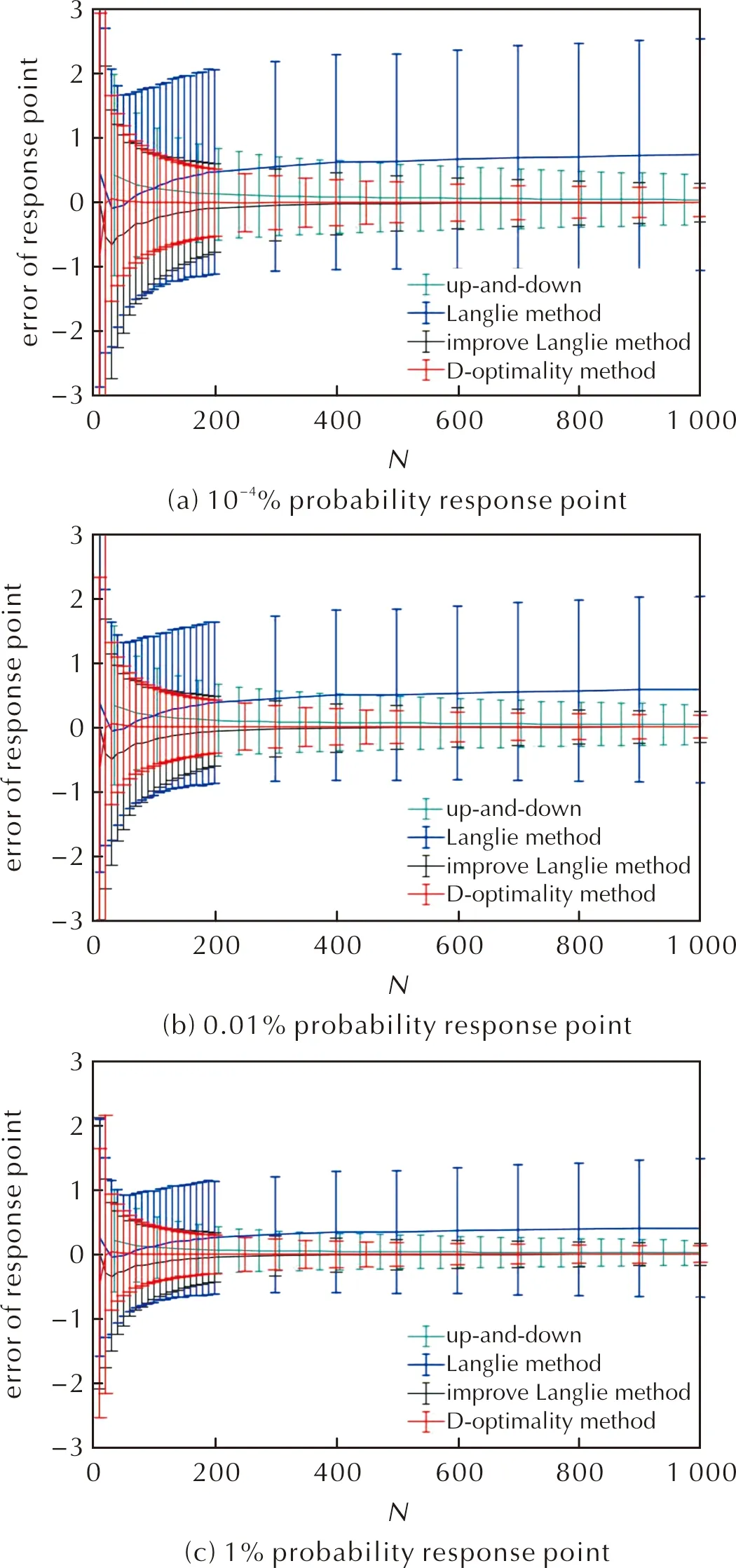
图5 不同数理统计方法小响应概率点结果比较Fig.5 Comparison of results of small response probability points of different mathematical statistics methods

表1 典型试验次数下10-4%概率响应点测算误差68.26%置信区间对比Table 1 Comparison of 68.26% confidence interval of 10-4% probability response points error under typical test times
结果显示,最优化D法对小概率响应点的测算准确性优于改进的兰利法,其在较少的250次试验内,可将E1ppm的测算误差的68.26%置信区间控制在0.456以内,使其相对误差小于10%。综上所述,最优化D法是四种数理统计方法中最适合静电感度试验的方法;优化和改进的兰利法具有操作便捷的优点,试验中的计算复杂度远低于最优化D法,其将测点集中在较小和较大概率响应点的改进思路,可为进一步优化静电感度试验数理统计方法提供参考。
5 结 论
(1)通过蒙特卡罗法计算机模拟试验,分析了基于现有典型数理统计方法进行静电感度试验的特点:升降法操作最简单,可对静电感度分布均值和方差进行较准确测算,但对初值和步长选择敏感,稳定性差;兰利法也具有操作简单的特点,可快速获得分布均值,但对方差的测算误差较大;最优化D法操作难度和计算复杂度较高,但对感度分布均值和方差测算准确性和稳定性都最高;增加试验次数可提高升降法和最优化D法的测算准确性。
(2)对比研究发现:最优化D法可在较少的试验次数内最准确且稳定地测算静电感度分布,在250次试验内可将E1ppm的测算相对误差的68.26%置信区间控制在10%以内,能准确表征火炸药静电最低引燃能量,为火炸药静电安全风险的定量化分析提供基础数据。但其使用过程需要进行大量复杂数学计算,试验时对人员技术能量要求较高,不适合作为常规静电感度试验的方法,未来可研发专用试验程序软件,自动完成复杂的测点刺激量计算和试验结果计算等过程,辅助操作人员基于最优化D法开展静电感度试验。
(3)优化和改进后的兰利法,突破了传统静电感度试验方法测点集中在50%概率响应点的思路模式,将测点分散在约30%和约70%概率响应点周围,在程序设定和计算复杂度远低于最优化D法的同时,达到与其相似的准确性。
(4)提出的分散测点的思路可有效测算方差的准确性,可作为未来进一步研究静电感度试验方法和程序的基础,以期建立一种新的感度试验数理方法,在提高极小概率响应点测算准确性的同时,具有较为简单、可操作性强的特点,方便用于常规静电感度试验。
