仿生扑翼齿轮组设计及动力学分析
2023-04-04丁长涛
徐 涛,丁长涛
(浙江工业职业技术学院 机电工程学院,浙江 绍兴 312000)
面对工作任务复杂、环境多样等原因,催生出一种新型的仿生扑翼机构,即在飞行方式上进行创新,而如何解决扑翼动力传动问题是众多学者需要攻克的难题。国外学者Saxena 等[1]研究了齿轮传动转子系统的动力学特性及啮合刚度对齿轮转子系统固有频率和振型的影响。通过振动特性来检测齿轮齿面故障,发现裂纹程度不同对齿轮转子系统模态特性和频率响应函数的影响。Yang 等[2]利用ANSYS 分析装配线性模态求得齿轮系统频率及模态振型,得知齿轮系统固有频率位于2 个临界状态的频率之间。崔永霞等[3]考虑齿面接触应力大导致齿轮振动进而使齿轮失效损坏,对直齿圆柱齿轮在不同载荷、频率激振下开展了谐响应振动分析,结果表明齿轮最大齿面接触应力与激振频率呈正比。李世慧等[4]考虑到齿轮体积、重量、数量增加及空间成本制约,基于MASTA 和Workbench 设计分析了在满足轻量化标准下的行星齿轮箱的强度、动力学分析。Zheng 等[5]利用ANSYS Workbench 对齿轮泵进行接触应力、模态分析,得知齿轮泵最大接触应力位置即最容易发生疲劳失效的位置。Kadam 等[6]通过试验模态分析发现直齿圆柱齿轮由于材料性能变化固有频率改变,以此来实现齿轮的轻量化设计。何育民等[7]发现双齿啮合时有冲击力产生且啮合进出时振动会加剧使得振动强烈。Liu 等[8]建立了船用齿轮箱有限元模型,进行了模态分析及实验对比,发现两者吻合程度较高,最大频率误差为4.04%。王东升等[9]基于ANSYS Workbench 分析了齿轮箱箱体的动态响应特征,结果发现在激励频率为390 Hz 左右时箱体轴上部肋板发生共振的概率较大,在设计相关部件时应避开系统固有频率。王园[10]基于变桨减速器的传动原理对减速器齿轮的部位进行建模并在Workbench 软件中开展静力学分析。Fan 等[11]在SolidWorks 中建立了差速器的几何模型并利用ANSYS 进行了强度校核和模态分析。结果表明,差速器齿轮副的最大应力模拟结果为624.14 MPa,齿轮副工作频率远低于第一固有频率。Ericson 等[12]采用试验模态对直齿行星齿轮的平面动态特性进行分析,并对有限元结果进行了对比。
已有研究仅通过单一角度考虑扑翼机构传动,并未综合考虑扑翼在真实飞行工况时所受外界因素影响。本文拟通过单驱动传动机构实现扑翼多自由度运动,依据生物尺度率优化设计齿轮组结构并考虑真实飞行工况进行模态、谐响应分析,更加深入剖析齿轮组强度、应变、位移、频响应状态,为研制仿生样机提供理论参考。
1 齿轮组模型设计
仿生扑翼机构采用双曲柄双摇杆机构配合齿轮减速机构以实现旋转运动至拍打运动的转换。而齿轮组配合对于扑翼运动平顺可靠起到至关重要的作用,包括齿轮的尺寸参数、传动比、体积重量、结构强度、疲劳极限及装配体啮合传动和共振响应等。以中型鸟海鸥为原型,根据生物尺度率及展弦比设计齿轮组,参数见表1。

表1 齿轮组参数
根据齿轮组参数并基于SolidWorks 进行三维建模,同时考虑样机整体质量且不影响整体结构强度将齿轮设计为轮辐式,三维模型如图1 所示。
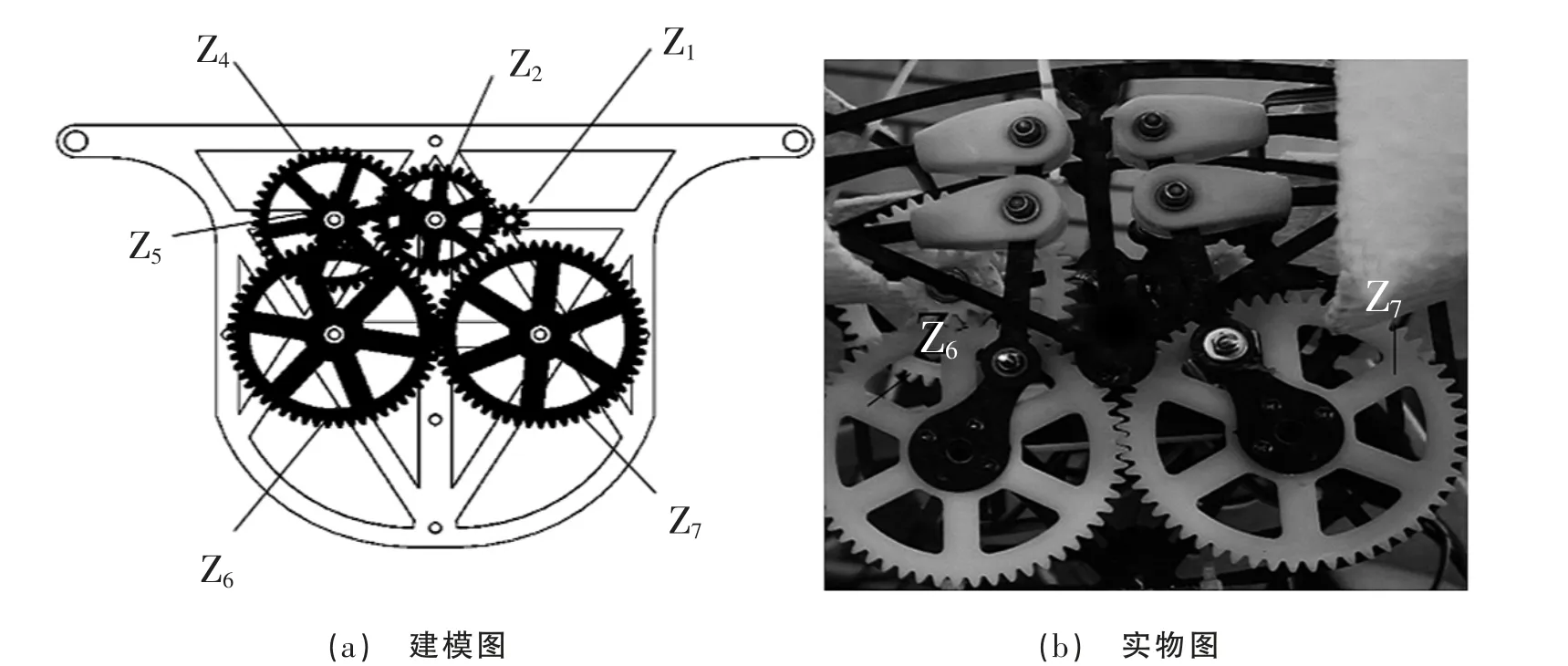
图1 齿轮组模型
2 模态分析
2.1 理论计算及前处理
模态分析是动力学分析的基础,固有特性对动态负载、响应及系统的振动形态均有重要影响。定义齿轮啮合运动为扭转振动模型将其等效为单自由度系统振动。系统分析模型由下式(1)(2)确定
两式联立,求解可得
由于Z6、Z7齿轮分别连接扑翼左右侧曲柄摇杆机构,相对于传动齿轮受力更加复杂,为了使扑翼实现多自由度运动在齿轮组中独立离散出主动轮Z6、从动轮Z7进行分析,为了使得模拟更加接近工程实际,在模态分析预处理前对齿轮施加预应力。齿轮组采用自动非结构化网格模式,非结构化网格具有良好的延展性,计算周期短不浪费计算资源。由于齿轮组啮合传动接触应力对模拟结果有较大影响,为了提高计算精度,对齿轮组啮合传动面进行网格加密处理。最终模型生成总网格数为60 841,节点数为10 806,最小网格在0.5 mm以上,求解计算采用Mechanical APDL,满足计算要求。
2.2 结果分析
建立齿轮副需要分析齿轮节点啮合的某一时刻对齿轮副建立摩擦接触,接触面为Z6齿面,目标面为Z7齿面,摩擦系数0.15。根据模型理论计算施加运动副载荷为10 N/mm,角速度为35.2 rad/s,齿轮固定孔施加预应力为1 MPa,设置完成后进行求解计算得到前18 阶部分固有频率值,见表2。
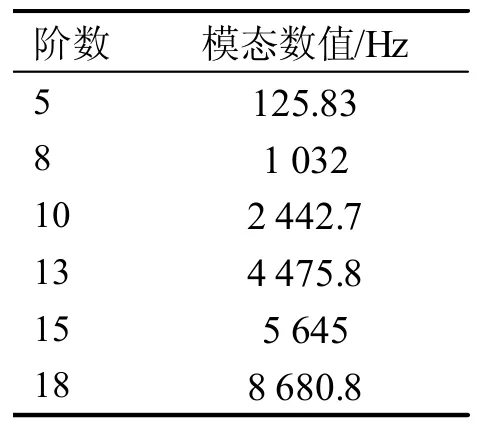
表2 前18 阶部分固有频率值
前18 阶部分模态振型如图2 所示,图2(a)为第5阶模态可以看出轮齿啮合处沿z 轴方向发生弯曲但变形程度不明显,在固有频率125.83~1 032 Hz 激励下,齿轮啮合过程相对稳定,共振现象不产生。由于轮齿固定孔施加了固定约束,使得装配体呈现由啮合处向外延伸的折叠变形,变形区间值域在0.7~198 mm 之间;图2(b)为第8 阶模态振型沿y 轴方向的弯曲变形,振型与5 阶类似但变形程度加剧;从第10 阶模态、13 阶模态发现齿轮发生了严重的弯曲扭转变形且最大变形量均在齿面及齿根位置处,其值分别为283、370.85 mm。从图2(e)发现第15 阶模态振型是沿y 轴的反向大挠度弯曲但扭转程度不明显,变形程度由齿轮固定孔往圆周方向递减再递增的趋势,呈“凹”状。第18 阶模态振型在轮齿啮合处沿x 轴呈挤压变形且整体型变量较大,齿根及齿面部分也完全重合过盈。
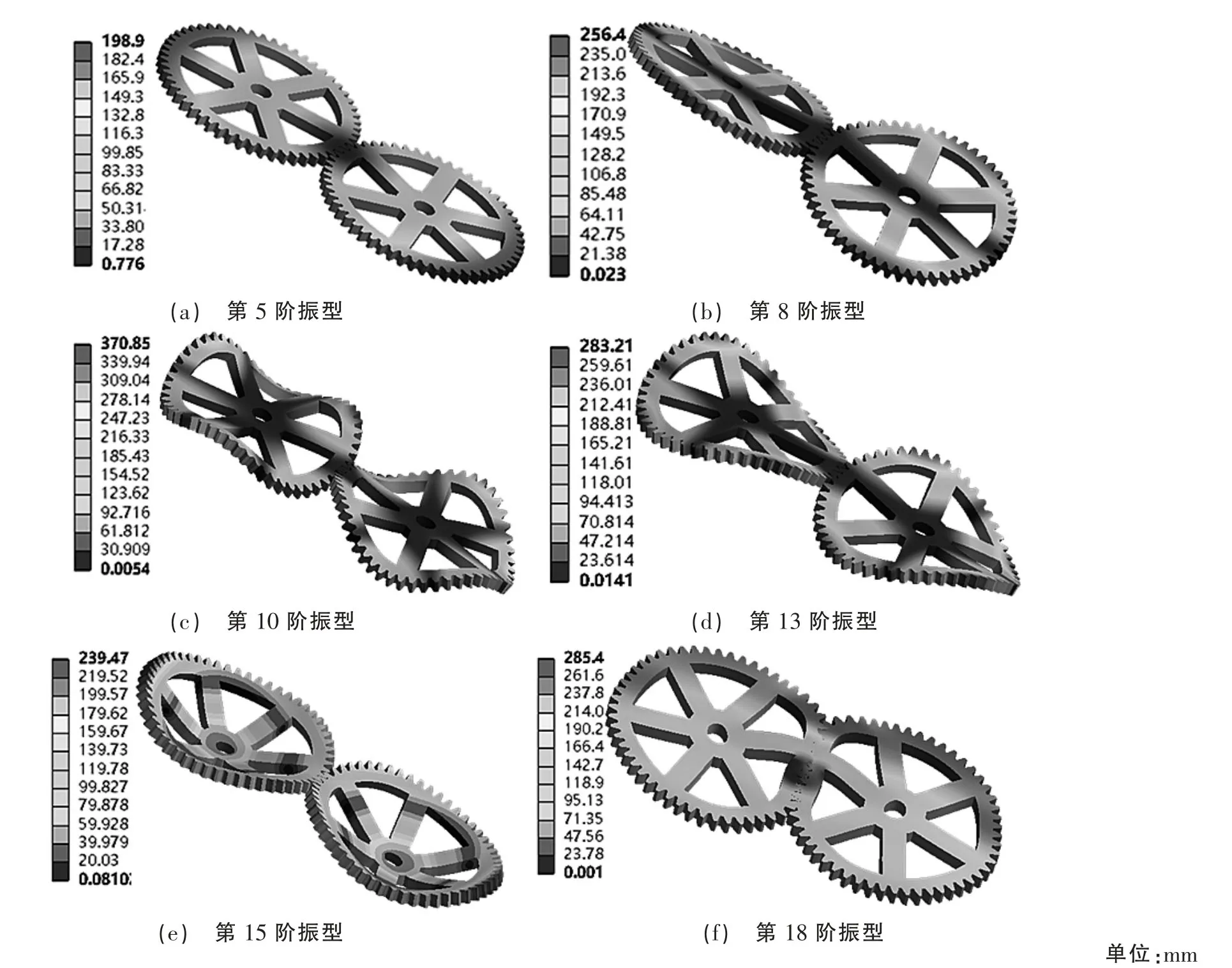
图2 模态振型图
从上述分析可知,齿轮传动失效形式伴随轮齿啮合弯曲、扭转和挤压变形等,在满足齿轮组结构强度、疲劳极限情况下应避开齿轮装配固有频率,避免因系统产生共振失效。
3 谐响应分析
模态分析研究结构得到动力学基本特性与结构所受载荷无直接联系而谐响应分析可以在不同持续频率的周期荷载作用下得到动力响应,计算结果与载荷直接相关,可以放大模态中不明显的频响特性。所受载荷为周期性简谐载荷从而可知外界激励频率与固有频率达到共振时模型振幅的具体参数。齿轮谐响应分析基于Workbench Harmonic Response 模块开展,计算采用模态叠加法即通过线性叠加各阶模态振型求得系统响应。虽然计算周期较长,但频率响应会更精确地反映出模型固有特性频率。
阻尼系数为0 及阻尼系数为0.05 的齿轮组啮合等效应变如图3(a)、(b)所示,由图3(a)可知等效应变值域范围在0.014~348.2 MPa 之间,整体应变较小且无突变迁跃。由于施加了固定约束限制了齿轮x 轴向自由度,应变较大区域出现在齿轮啮合面及齿轮固定圆孔处,最大应变出现在齿根部位。图3(b)发现应变值有降低趋势,值域范围在0.017~323 MPa 之间,平均应力在50 MPa 左右,比无阻尼状态幅值降低约7.2%且应变区域明显减少。
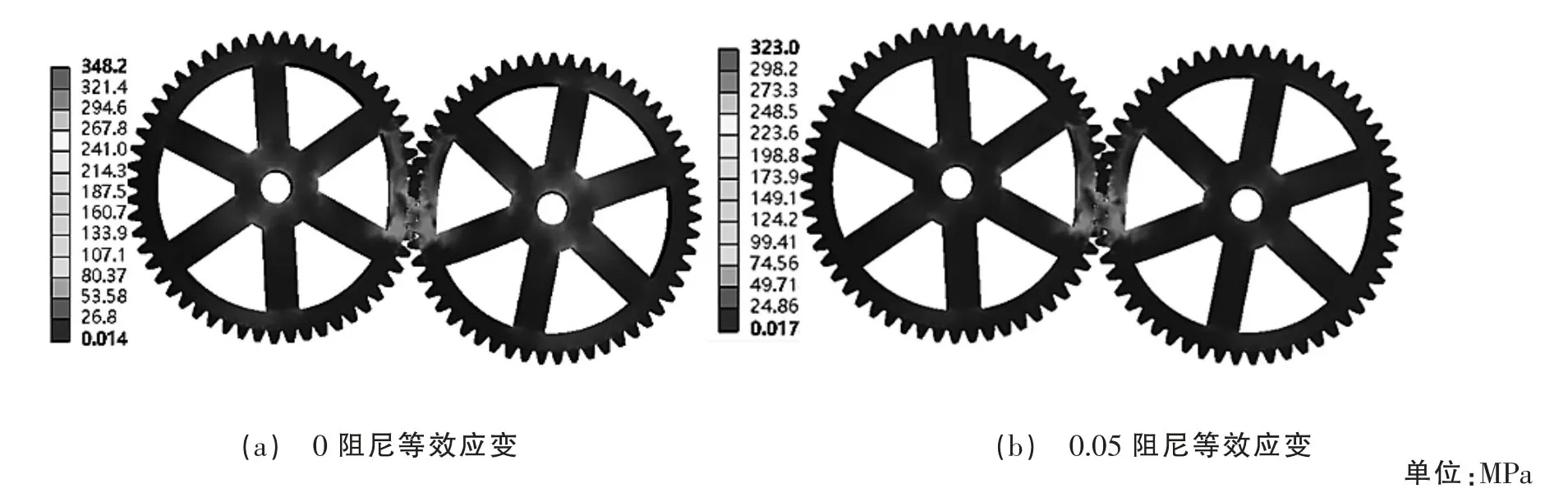
图3 不同阻尼系数应力变化
图4(a)、(b)为齿轮组形变位移图,可知整体形变量较小,值域范围在0.004~0.06 mm 之间,不同阻尼系数下区别不大,比无阻尼状态幅值降低约3.1%且形变趋势基本相同,均从主动轮坐标系左侧逐渐递增至右侧方位,从动轮反之。齿面处呈最大形变,整体表现为挤压形态。
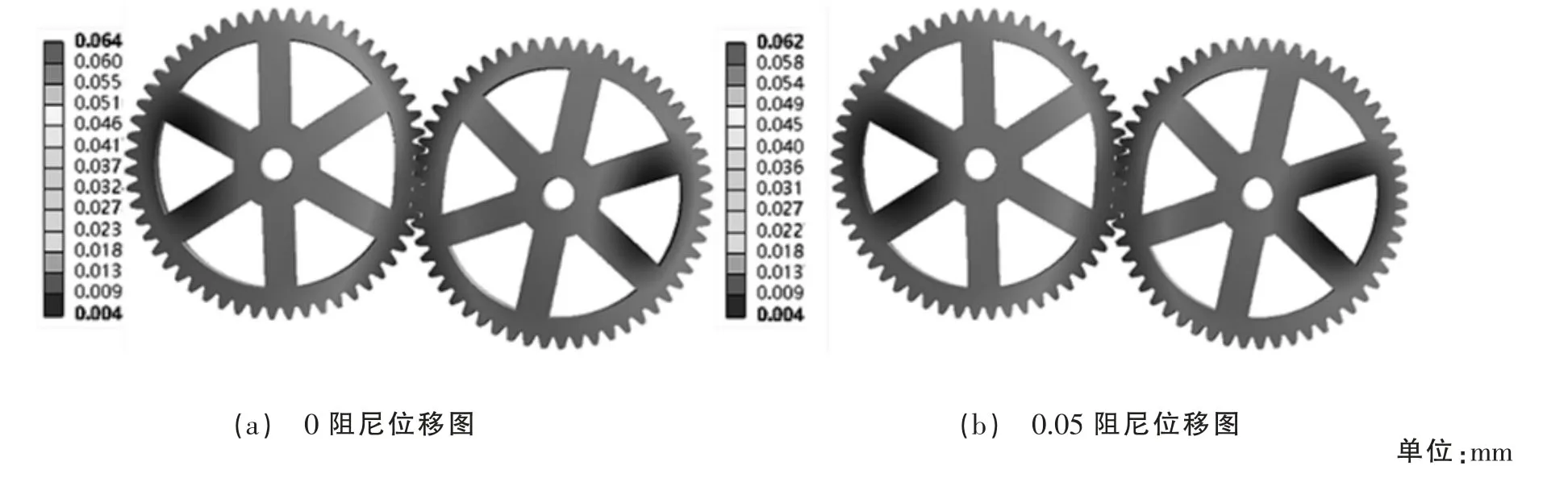
图4 不同阻尼系数位移变化
基于模态叠加法的谐响应分析对频率的选取范围至关重要。将模态的频率为谐响应分析的1.5 倍即设置计算频率为0~6 000 Hz,每60 Hz 计算1 次,计算步长为100 次。为了更加直观清晰地表明齿轮啮合过程中不同频率下的动态响应,节点随频率位移、相角变化如图5 所示。其中细点线表示阻尼系数为0 时的频率-位移变化曲线,粗实线表示阻尼系数为0.05 时的频率-位移变化曲线。由图5(a)发现,在850 Hz 激励下节点位移达到最大值,为0.026 mm;频率分别在3 600 Hz、3 800 Hz 时位移曲线出现不同程度的“尖峰”,当频率为5 600 Hz 时位移再次达到最大值。对比模态分析发现,谐振激励均发生在固有频率附近,且低阶频率突变多于高阶频率,低阶比高阶频率对系统的振动特性影响较大,而减小共振现象发生需避开其固有频率。而当增加阻尼系数后发现曲线整体较为光顺且多个峰值消除,平均位移约0.035 mm,在节点频率为3 600 Hz 时位移降低程度最大为47.8%,但在低阶频率时最大位移值几乎没有改变。
由图5(b)分析可知,无阻尼状态下在多个频段存在相位突变,当扫频区域在60~850 Hz、3 600~4 000 Hz时,存在180°相位差的持续峰,在1 700 Hz 附近仅存在1 个180°相位差的尖峰。当阻尼系数增加时曲线变化更加平滑,除低阶频率波动外其余阶段变化较小,平均相位范围保持在100°左右,整体表现较为稳定。
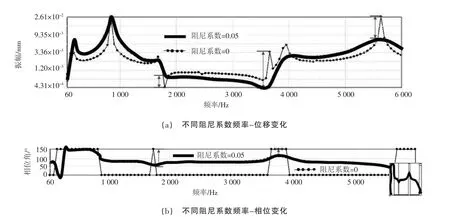
图5 谐响应变化曲线
由图6 可知,在放大扫频角度为720°下850 Hz激励频率的归一化向量发现,不同阻尼系数的频响特性有所不同,无阻尼状态时y 向、z 向完全重合,x 向为0;增大阻尼系数可以使得动态响应状态发生偏移,y 向、z 向偏移约为一个扫频60 Hz,避开了共振激励频率。
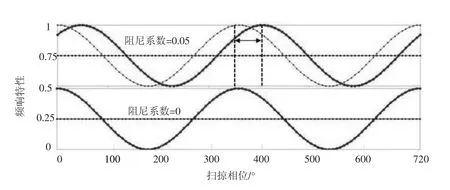
图6 不同阻尼系数扫频变化
4 结束语
本文设计了一种仿生扑翼机构齿轮组结构,基于Workbench 展开模态及谐响应分析,得到了齿轮组的等效应变、形变、固有频率及频响应特性,验证了模型结构合理性,为仿生样机研制提供理论支持。
1)齿轮啮合前18 阶模态振型发现低阶频率下齿轮变形不明显,振型多为弯曲、扭转变形;在7 阶模态时频率突变增幅达82%,而在1 711.5~9 439.1 Hz 激励下齿轮出现挤压、弯扭横振的复杂变形。
2)通过谐响应分析对比不同阻尼系数发现,阻尼系数的增加可以降低齿轮局部接触应力,减小应变范围,比无阻尼状态幅值降低约7.2%;可以降低齿轮位移变形,减小幅值约3.1%。
3)通过谐响应细化不明显的频响特性,分析齿轮啮合各节点随频率变化位移、相位响应发现峰值均出现在固有频率附近,进一步验证了模态分析合理正确。在850 Hz 激励下节点位移达到最大值,表明在齿轮设计时应避开固有频率防止共振现象发生。
