一道解析几何高考题的背景思考与推广
2023-04-03浙江省象山中学315700杨育池
浙江省象山中学 (315700) 杨育池
1 试题呈现

这是2009年高考湖北卷理科数学第20题,不少文章对问题的解法进行过研究,本文只就试题的第二问中λ的值蕴含的背景及几何意义进行更一般的阐述.
2 背景思考
极点、极线是《高等几何》中的重要概念,在揭示二次曲线的性质有着强大的威力,二次曲线很多重要的几何性质均与之有关.下面先简要介绍关于极点、极线的基本知识与相关结论.
极点与极线的代数定义若二次曲线Γ的方程为Ax2+2Bxy+cy2+2Dx+2Ey+F=0,则称点(x0,y0)与直线l:Ax0x+B(x0y+xy0)+cy0y+D(x+x0)+E(y+y0)+F=0为二次曲线Γ的一对极点和极线.
如图1,不在二次曲线Γ上的点A作曲线Γ的两条割线,依次交曲线Γ于点C,D,E,F,直线CF,DE交于点B,直线CE,DF交于点H,则直线BH为点A关于Γ的极线,点A是直线BH关于Γ的的极线.这是极点、极线的几何定义.应该特别注意,互相平行的直线交于射影平面上的无穷远点;若点A在二次曲线Γ上,则Γ在点A处的切线是A关于Γ的极线l.在欧氏距离下,过点A的直线与极线l、曲线Γ的交点具有分割线段成比例的性质.

图1


图2
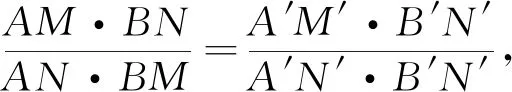
现将本文中的问题置于高等几何背景下,我们可以发现,点A(a,0)与直线l:x=-a为关于抛物线y2=2px(p>0)的一对极点极线.因此,本题表面上考查三角形面积之间的确定关系,其实质是在二次曲线的极点、极线背景下,将点列经透视变换成相关点列后,考察对应线段之间的比例关系.
3 结论推广
在设计试题时,将极点设置在曲线的对称轴上,这样其对应的极线则是轴的垂线,在坐标运算上较为简单些.由于结果为定值,促使笔者进一步思考,对所有的二次曲线的一般位置的极点、极线是否存在同样的数量关系?与极线垂直的直线具有平行性,如果将其垂线推广为与极线相交的平行直线是否还能成立呢?回答是肯定的,即如下命题.
命题1 直线l是点A关于二次曲线Γ(A∉Γ)的极线,过点A的直线交Γ于点M,N,自点M,N作两平行线交l于点M1,N1,记△AMM1,△AM1N1,△ANN1的面积分别为S1,S2,S3,则S22= 4S1S3.

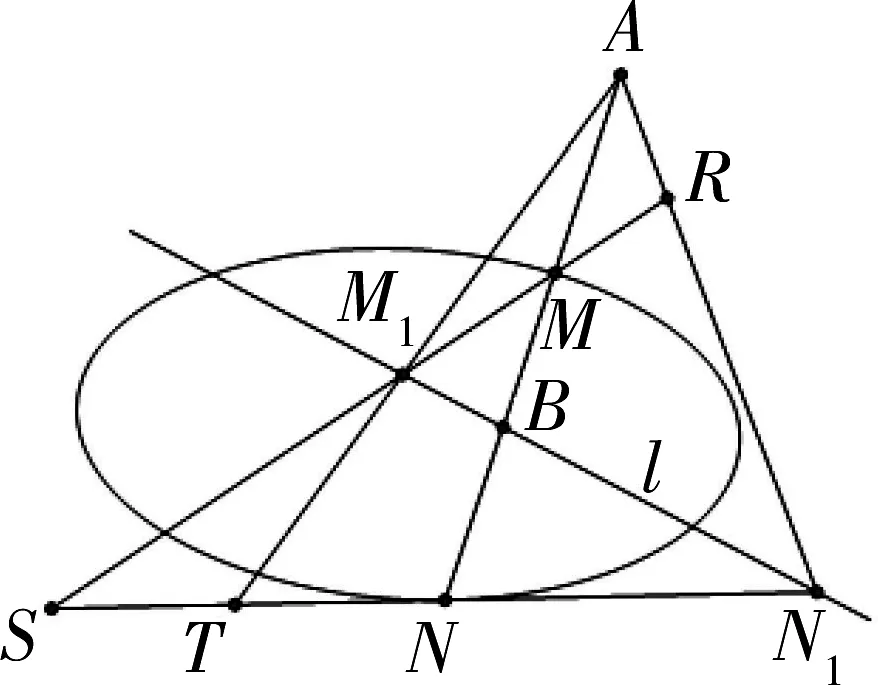
图3
同理,以点A为透视中心,点列N1,T,N,S与点列R,M1,M,S透视对应,点N为TN1的中点.由MM1//NN1,有∠AM1R=∠ATN1,∠AN1N=∠ARM1,于是,
两式相乘即得S22= 4S1S3.
命题2 直线l为点A关于二次曲线Γ(A∉Γ)的极线,过点A的直线交Γ于点M,N,交l于Q,点B为l上异于点Q的动点,分别过M,N作AB的平行线交l于点M1,N1.若△BMM1,△BMN,△BNN1的面积分别为S1,S2,S3,则S22= 4S1S3.

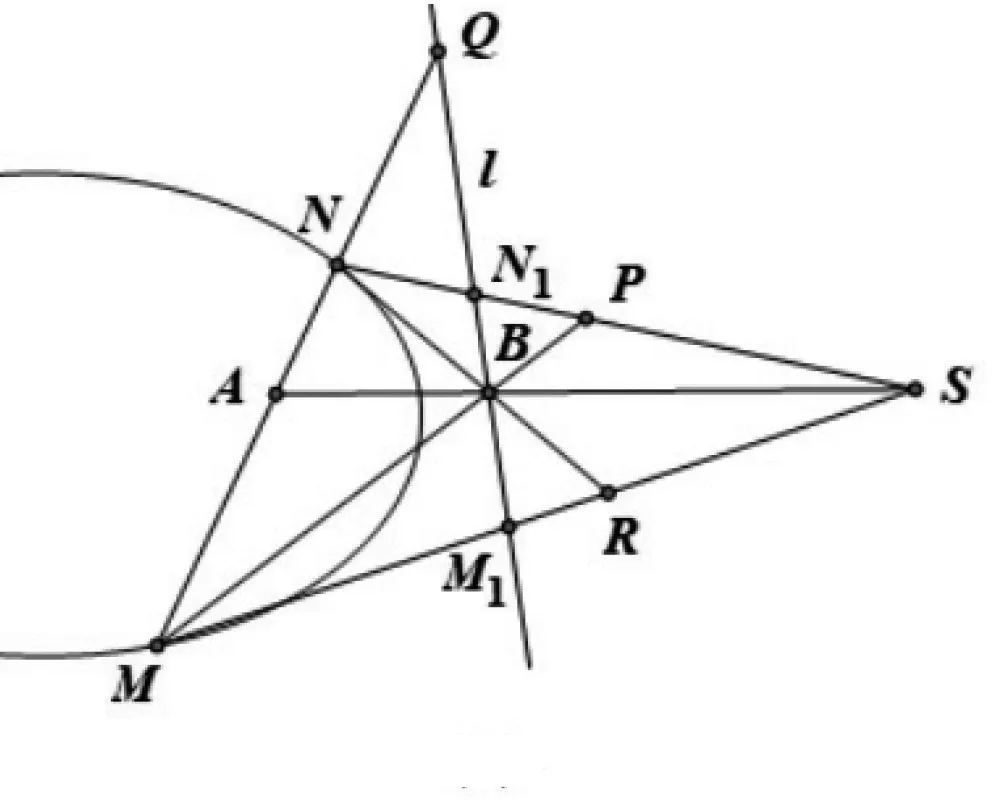
图4
显然,以上证明只涉及点A与直线l是关于Γ的一对极点极线,点A在二次曲线Γ的内部还是外部不影响结论.
4 再次推广
两个命题初看构形上相异,而结果完全相同,让人产生一种奇异的美感,但仔细考虑就会发现这两个结论其实是一致的,其奥妙在于,如图4中以点S为透视中心,则点列(A,Q,M,N)对应点列(B,Q,M1,N1),于是,当(A,Q,M,N)调和时,(B,Q,M1,N1)也为调和点列.由于点S为无穷远点,因此,两个结论可统一为:若四边形存在一组对边平行,另一组对边中的一边的两顶点与其对边的交点,和这一边上的第四个点构成调和点列时的性质,完全隐去二次曲线这一图形约束,则进一步得到一个初等几何结论.
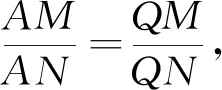

图5
注意由点M,M1,N,N1所构成的四边形对应的图形有多种,不一定是四边形MM1NN1.
证明:记直线AN1,MM1交于点P,AM1,NN1交于点T.由MM1//NN1得,
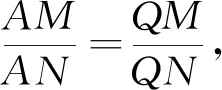

所以两式相乘有S22= 4S1S3.
