位移法典型方程及数值分析在门窗多点锁闭系统中应用

戴红亮，邱铭，马思远，付相球，王全

（1.建筑安全与环境国家重点实验室，北京 100013；2.建科环能科技有限公司，北京 100013）

0 引言

目前关于门窗多点锁闭系统计算方法可供参考的资料极其匮乏，甚至在所有的门窗标准规范中也并未涉及，这无形中给从事门窗设计的同仁带来不便。门窗多点锁闭系统五金在建筑外窗的气密性能、隔声性能、保温性能等方面发挥重要作用，所以多点锁闭系统五金应用越来越广泛，而多点锁闭系统理论研究却捉襟见肘，戴红亮采用了力法对多点锁闭系统五金进行解析，计算多点锁闭系统五金单个锁闭点的集中力及两个锁闭点间杆件的最大位移量[1]，这也是目前多点锁闭系统五金在静定结构计算中较为完整的计算方法[2]，但是该法计算过程较为复杂，在实际应用中并不方便。本文在以前文献的基础上采用位移法典型方程对多点锁闭系统五金进行分析，此法较力法具有计算简便、节省时间的优势[3]。

1 多点锁闭系统五金

门窗多点锁闭系统五金配件是相对单点锁闭五金配件而言，包含：传动锁闭器如图1 所示、多点锁闭器以及相关的内平开下悬五金系统等[4-5]。本文主要探讨门窗开启扇如图2所示在风荷载作用下该如何确定其力学模型以及在此基础上如何分析锁闭点受力状态，在此着重探讨窗扇执手侧边梃上（受力杆件）配置4 点锁如图3 所示情况下[6]，在风荷载作用下锁闭点的支座反力的计算方法。下面介绍一下4 点锁的受力状态，4 点锁是在门窗执手（合页）侧的竖向边梃上安装具有4 个锁点的传动锁闭器，关闭后，该边梃与其对应的边框通过锁点与锁座的搭接而实现锁闭窗扇的功能[7]。通常情况下，端部锁点距离边梃端部为100～250mm，简化力学模型如图4 所示。

图1 传动锁闭器

图2 开启扇

图3 四点锁

图4 力学模型

2 四点锁受力分析

为了更加清晰地说明多年锁闭位移法典型方程在门窗多点锁闭系统中的应用，采用四点锁作为分析对象。此结构为二次超静定结构且不等跨，静力平衡方程无法求解，笔者选用位移法来分析计算。目前求解超静定结构的经典方法有力法和位移法，而力法较位移法应用起来繁琐，计算过程复杂，故采用位移法进行4 点锁受力分析，4 点锁就是在窗扇（门扇）的边梃上安装四个锁点和锁座，锁点和锁座视为多跨连续梁支座，4个锁闭点就意味着有4 个支座。将竖向边梃视为具有4 个铰支座的多跨外伸梁，首先确定其力学模型，见图4，下面计算4点锁开启扇边梃在风荷载作用下的支座反力，即锁闭点水平方向的剪力。

假设该门窗开启扇的竖向边梃为外伸多跨连续梁，该边梃配置4 个锁点，且受到的均布线荷载为2N/mm，各跨长度分别为：l0=130mm，l1=550mm，l2=200mm，l3=550mm，l4=130mm总跨度为1560mm，下面分析4 点锁受力状态。

2.1 基本未知量和基本体系确定

首先建立基本体系如图6 所示，在原结构基础上，支座B、C 处施加刚臂，限制支座转动。根据节点B的角位移Z1，节点C的角位移Z2，节点B，C附加约束得到基本体系，为了选用位移法，将外伸梁两边跨l0，l4去掉，如图5～8 所示。

图5 原结构

图6 基本体系

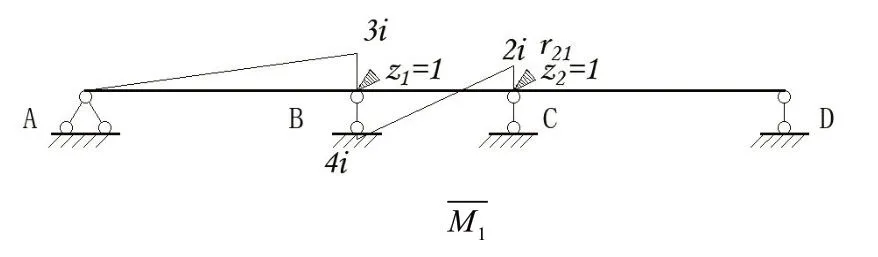
图7

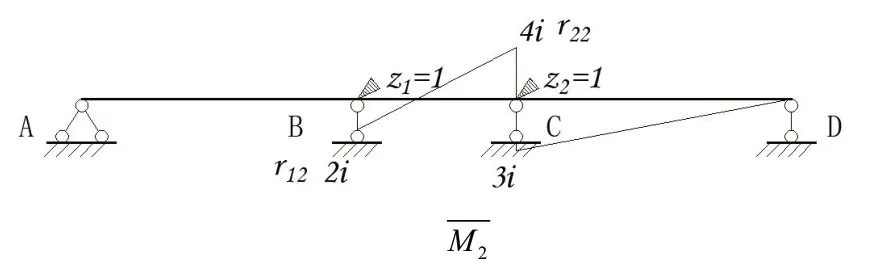
图8

2.2 位移法方程

根据基本体系，建立位移法典型方程如公式（1）（2）所示。

2.3 计算 r1 1,r2 2,r2 1,r22

2.4 计算外荷载作用下弯矩R1P，R2P

基本体系在荷载作用下，计算杆端弯矩，荷载作用下MP图如图9 所示。

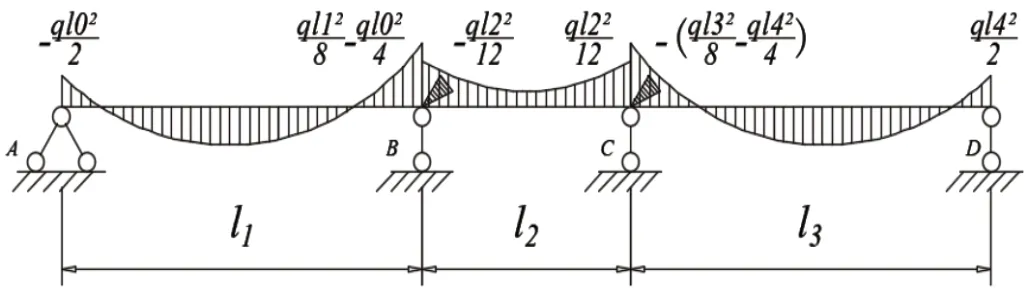
图9 Mp

采用力法以及力矩平衡关系，结合图9 可得如下固端弯矩值：

由节点B的力矩平衡可得：

由节点C的力矩平衡可得：

2.5 计算z1，z2

将i,i',i''及R1p,R2p代入公式（1）（2），可得公式（3）和（4）：

2.6 计算支座弯矩并作M 图（如图10 所示）

图10 M 图

3 计算锁闭点支座反力

3.1 根据力矩平衡，可得：

3.2 计算锁闭点支座反力

RA=757.42N，RB=802.58N，RC=802.58N，RD=757.42N。

4 数值法锁闭点受力分析

本数值分析基于学生版ANSYS workbench 2021R1CAE仿真平台，针对多点锁闭系统五金的受力情况采用有限元法进行分析，有限元法是求解数理方程的一种数值计算方法，是将弹性理论、计算数学和计算机软件有机地结合在一起的一种数值分析技术，是解决工程实际问题的一种有力的数值计算工具[8]。

通过有限元法与解析法对比，分析计算结果存在的差异及原因，以及在实际工程中该如何处理，为行业同仁在工作中遇到此类问题后提供一种有效解决途径，至于选择何种方式，笔者更加倾向于数值法，因解析法计算过程繁琐，专业程度要求较高，笔者在此并不推荐。

门窗开启扇受力杆件的截面为非对称几何图形，在受到垂直玻璃版面方向的外力后，杆件发生两个方向的位移，这就意味着有两个方向的支座反力，这与解析法计算多点锁闭系统五金内力及支座反力存在差异，解析法计算时默认杆件截面为对称的等直杆。不必考虑杆件的截面型式，只需知道杆件的长度、支座型式及外荷载即可求解杆件内力及支座反力，但是数值计算中必须建立实体模型方可进行计算，理论上来讲，数值计算更符合工程实际情况，而且计算效率较高，节省分析计算时间。为了更加详细说明数值分析法在建筑门窗五金系统受力分析中的应用，笔者采用三种不同网格数量的分析模型进行计算，一种为系统默认网格划分型式，其他两种为加密网格划分型式，通过三种分析法进行对比，分析网格数量对计算结果的影响，从而达到分析的科学性、合理性，为行业同仁在采用数值法分析时提供依据。

数值分析前，对门窗五金及窗扇做一下简单介绍，便于大家更加深入了解门窗锁闭系统及其力学模型的确定方法，窗扇不能独立存在于实际工程中，其必须通过合页（铰链）将扇的边梃和框连接在一起，并以合页（铰链）为轴自由转动如图11所示。锁闭状态下，锁闭点及合页（铰链）将扇与框紧密连接在一起，形成一个完整的闭合体如图12 所示，计算多点锁闭系统五金受力时，窗扇锁闭侧的边梃视为外伸多跨连续梁且各个跨度并不相等，1 个锁点与1 个锁座组成1 个锁闭点，数值分析时可将锁闭点视为铰支座。

图11 合页连接

图12 窗扇锁闭

4.1 建立几何模型

选用常用铝合金型材断面，CAD 软件建立三维实体模型，设置四个约束，约束间距分别为：l0=130mm，l1=550mm，l2=200mm，l3=550mm，l4=130mm，总长度为1560mm，杆件截面及杆件长度见表1，分析模型见表1。

表1 分析模型

4.2 网格划分

4.2.1 网格尺寸

网格划分见表2。

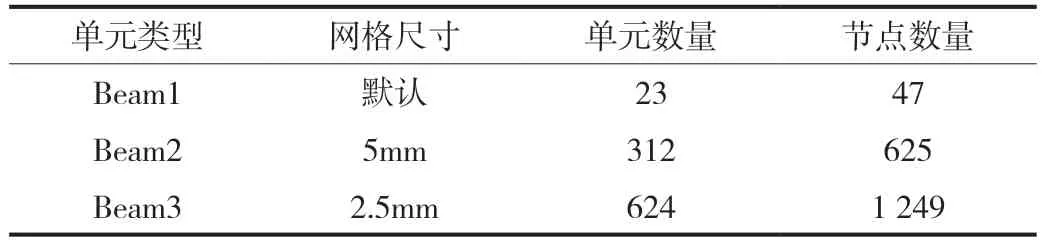
表2 网格划分

4.2.2 分析模型

分析模型见表3。

表3 分析模型

4.3 计算过程

4.3.1 荷载工况

将执手侧边梃视为多跨外伸连续梁，并满布均布荷载，其值为2N/mm，从左到右支座的施加约束型式为：A 支座限制其三个方向的平动约束，释放绕Y、Z 轴的转动约束；B、C、D 支座限制Y 和Z 方向的平动约束，释放X 轴方向的平动约束，同时释放绕Y、Z 轴的转动约束[9]，荷载及约束具体情况见表4。

表4 约束型式

4.3.2 支座反力及弯矩（默认网格）

（1）支座反力

锁闭点支座反力见图13 所示。

图13 锁点支座反力

通过数值分析计算，可以得出四个锁闭点的支座反力值，分别是：RA=760.29N，RB=799.71N，RC=799.71N，RD=760.29N。

（2）剪力、弯矩图

剪力及弯矩图如图14 所示。

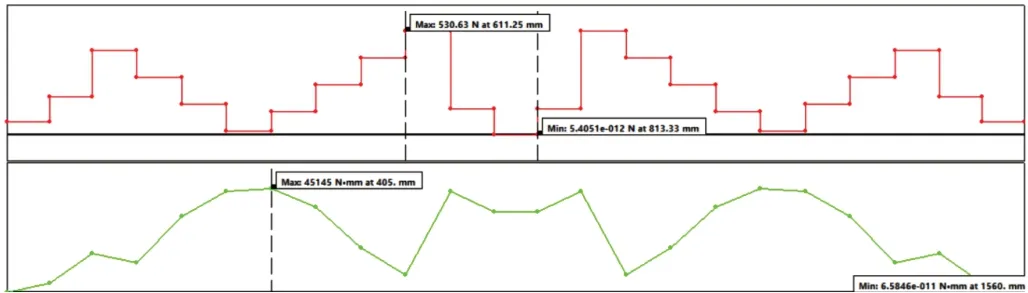
图14 剪力、弯矩图

最大弯矩发生在接近最大跨度的跨中，其值为：45145N·mm。

4.3.3 支座反力及弯矩（5mm 网格）

（1）支座反力

锁闭点支座反力如图15 所示。

图15 支座反力

通过数值分析计算，可以得出四个锁闭点的力值，分别是：RA=758.81N，RB=801.19N，RC=801.19N，RD=758.81N。

（2）剪力、弯矩图

剪力、弯矩图如图16 所示。

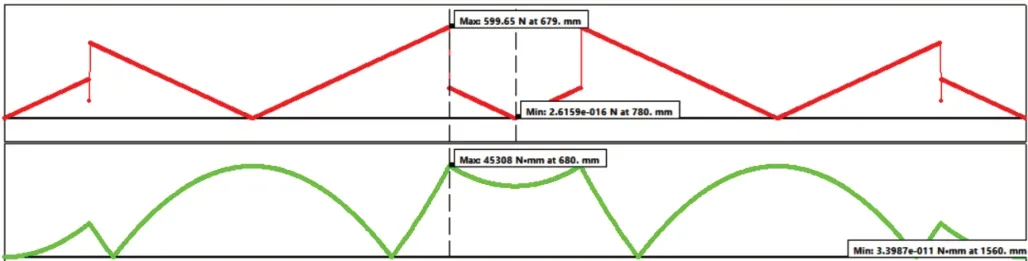
图16 剪力弯矩图

最大弯矩发生在靠近跨中的支座处，其值为：45 308N·mm。

4.3.4 支座反力及弯矩（2.5mm 网格）

（1）支座反力

锁闭点支座反力如图17 所示。

图17 支座反力

通过数值分析计算，可以得出四个锁闭点的力值，分别是：RA=758.8N，RB=801.2N，RC=801.2N，RD=758.8N。

（2）剪力、弯矩图

剪力、弯矩图如图18 所示。

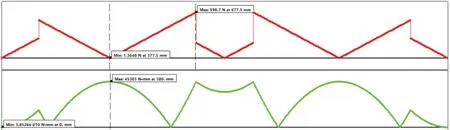
图18 剪力、弯矩图

最大弯矩发生在跨度最大值的跨中，其值为：45 301N·mm。

5 结果对比

经过以上分析，理论计算结果与数值分析结果基本吻合，差异在2‰以内，说明理论分析计算与数值分析方法均可行。

5.1 支座反力

支座反力如表5 所示。

表5 支座反力

5.2 弯矩

弯矩值如表6 所示。

表6 弯矩值

6 结论

基于以上分析，解析法计算过程较为复杂，效率较低。建议采用数值法进行多点锁闭系统五金计算。通过理论分析及数值计算，得出这样结论，即在外荷载作用下，当最大跨度满足正常使用功能极限状态时，锁闭点分布并非等跨或近乎等跨布置最为合理，而是跨中的锁点间距应小于与其相邻跨的锁点间距，即隔跨相等或近乎相等原则，这样方可使锁闭点受力更加趋于均匀，减小受力差异。分析中不难发现建筑门窗多点锁闭系统五金受力分析较为复杂，锁闭点数量越多计算强度越大，这也是多点锁闭系统五金受力分析困难所在。正因如此，选择分析方法变得尤为重要，分析计算时有三种方法可供选择，力法是最基本的计算方法，但是最为繁琐 ；位移法是建立在力法之上的另一种有效途径，复杂程度略优于力法；数值法则是独立于力法与位移法之外的另一种可供选择的有效途径，同时其对操作者专业程度要求有限；笔者推荐使用数值法，此法的最大优势是计算简便、节省时间。然而在门窗五金应用设计中，必须通过合理的分析计算方能做出合理配置方案，而具体选用何种方法也是因人而异。希望通过本文介绍，能够为行业同仁提供一种解决门窗超静定结构计算的思路，提升门窗设计水平。