埋头弹高速冲击挤进入膛特性研究
2023-04-02师军飞钱林方陈红彬付佳维
师军飞, 钱林方, , 陈红彬, 付佳维
(1. 南京理工大学 机械工程学院,江苏 南京 210094; 2. 西北机电工程研究所,陕西 咸阳 712099)
0 引言
埋头弹是近年来迅速发展的新型弹药构型,弹丸被埋入药筒内部,弹药整体呈规则的圆柱体形状,长度相比同口径常规弹药大幅缩短,有助于火炮系统实现轻量化和自动化。埋头弹火炮的内弹道采用二次点火与程序燃烧控制原理,弹丸在克服拔弹力后先在导向筒内做自由加速运动,然后以较高的入膛速度冲击挤入膛线起始部,是典型的动态冲击挤进过程。而传统火炮采用的经典内弹道略去了弹带挤进膛线起始部的过程,假定当膛内火药气体压力达到启动压力时弹丸才开始运动[1]。冲击挤进时与坡膛的高速碰撞会对埋头弹弹丸的运动产生强扰动,挤进结束时的弹丸姿态会对弹丸后续的膛内运动规律产生直接影响,进而影响埋头弹火炮的射击精度。因此,对埋头弹火炮的内弹道进行建模,开展高速冲击挤进入膛特性的研究,对提升埋头弹火炮的射击精度有着重要的科学意义。
埋头弹入膛时的运动边界条件对冲击挤进过程产生重要影响。张浩等[2]对埋头弹的内弹道进行分析建模,对其内弹道性能进行了模拟。钱环宇等[3]建立了固体随行装药方案的埋头弹零维内弹道模型,针对试验方案进行了数值模拟,并针对其多参数变化进行了影响预测分析。Monreal-González 等[4]提出了一维内弹道模型,考虑燃烧过程中的界面摩擦、界面传热等因素给出了数值方法,与实验测试结果相比呈现出高精度。刘静等[5]针对模压可燃药筒进行了密闭爆发器实验,建立高压燃烧模型进行数值计算,获得了能量特性、燃速指数和燃速系数等可燃药筒的示性数。郭俊廷等[6]将可燃药筒视作内外层燃速不同的片状药,建立了半可燃药筒埋头弹的内弹道模型,将105 mm 埋头式榴弹射击装药方案作为输入参数进行数值模拟,并预测了105 mm 埋头式穿甲弹的弹道性能。
冲击挤进瞬间弹带在高温、高压和高速的作用下会产生强非线性的塑性大变形,弹带的材料性能和接触界面的摩擦系数会产生变化,通过测试的方式获得射击工况下的挤进规律非常困难,因此理论分析、数值模拟与实验室静态加载试验是目前主要的研究途径。理论分析方面,张浩等[7]基于埋头弹特殊的结构和动态冲击影响,分析了挤进时弹带表面的流动应力和摩擦系数,并讨论了挤进阻力等挤进参量变化对内弹道的影响。Sudarsan 等[8]采用量纲分析建立了大口径枪械短启动压力理论预测的通用模型,考虑了膛线、弹带、弹丸相关影响短启动压力的参数,并利用无量纲参数组之间的线性关系建立了模型并进行了验证。邹立波等[9]针对挤进过程界面间的摩擦特性提出了一种摩擦模型,考虑接触压力、相对速度以及温升导致弹带表层熔化的影响,分析了弹丸速度和弹带表层温度的变化规律。Ding 等[10]提出了一种火炮身管参数化几何建模方法和身管磨损有限元网格划分策略,通过建立热力耦合的瞬态有限元模型,来计算弹带的塑性变形和内弹道性能。数值模拟方面,程申申等[11]建立了内弹道与挤进有限元动力学耦合模型,对尼龙弹带的挤进阻力特性进行研究,给出了不同的弹带结构尺寸影响规律。郭俊行等[12]使用光滑粒子流体动力学(SPH)方法建立了发射模块药弹带挤进模型,仿真获得不同膛线形式和缠角的弹丸运动、挤进阻力和导转力矩等的变化规律,揭示了挤进过程的塑性变形机理。Shen 等[13]基于机枪身管寿命试验损伤数据,发展了一种新的损伤身管有限元网格划分方法,并针对各工况进行了热力耦合有限元数值仿真,通过试验验证了所提网格划分方法和有限元模型的准确性。马明迪等[14]使用光滑粒子-有限元(SPH-FEM)耦合方法,针对装填不到位、初始装填角度、弹炮间隙等因素进行了弹丸动力响应影响分析。李淼等[15]建立了挤进热力耦合模型,求解获得了挤进阻力、弹丸运动、膛压及弹丸摆动角的变化规律。Li 等[16]分别采用有限元(FEM)、有限元-光滑粒子(FEM-SPH)和耦合欧拉-拉格朗日(CEL)方法对弹丸挤进过程进行了数值模拟和对比。结果表明FEM-SPH 方法和CEL 方法在涉及挤进过程模拟的应用中具有优势。纪杨子燚等[17]建立了定装式弹丸的挤进有限元模型,针对不同的膛内自由行程对弹丸运动、弹体载荷和炸药的动态响应进行了分析。Hu 等[18]建立了火药燃烧和弹炮相互作用的耦合模型,通过设计正交试验研究了中口径火炮各结构参数对系统性能的影响,结果表明各结构参数中弹带宽度的影响尤为突出。Xin 等[19]建立了弹丸挤进过程的流固耦合模型,通过发射实验验证模型。对挤进系统的尺寸参数进行了敏感性分析和优化设计。Keinänen 等[20]和Toivola 等[21]基于有限元法和解析法分析了弹带结构和材料特性变化对身管应力的影响,并通过试验验证了数值仿真结果,结果表明弹带的结构型式和尺寸影响最大。Ding 等[22]采用3 种不同的本构模型对铜EFP 的成形性能进行研究,对比实验和数值结果,发现采用Johnson-Cook 本构模型结合失效模型和h-自适应算法是预测爆炸成型弹丸(EFP)轴向断裂的最合适的方法。实验研究方面,Wu 等[23]针对准静态及瞬态挤进使用截短身管和气体炮进行了实验研究,结果表明 低加载速度下的应变硬化以及高加载速度下的应 变率效应和热效应对挤进过程具有关键作用。Ritter 等[24]采用高速摄像和截短身管对小口径枪弹挤进过程进行实验研究,认为难以通过物理模型描述挤进运动,可以采用高阶多项式弹头的位移-时间曲线进行拟合。刘东尧等[25]进行了中口径埋头弹药的动态挤进实验,采用对位移数据2 阶微分的方法,获得了挤进阻力-位移曲线。许辉等[26]通过理论分析、实验研究和数值模拟相结合的形式开展枪弹动态挤进阻力模型研究,采用显式动力学有限元方法模拟枪弹动态挤进过程,利用多参数同步测量技术进行了动态挤进实验,验证数值模拟的有效性,通过构建动态挤进阻力模型,分析了影响挤进阻力的关键因素,并与数值模拟进行了对比。
目前对于挤进过程的研究对象往往是常规弹药的静态或准静态挤进,对于埋头弹这种高速冲击挤进过程的研究涉及很少。为了揭示埋头弹高速冲击入膛过程的力学机理和运动规律,本文在已有研究的基础上,建立了考虑可燃导向筒燃烧的埋头弹火炮零维内弹道模型,计算得到了弹丸冲击入膛时的速度和弹底压力边界条件;基于FEM-SPH 耦合算法建立了高速冲击挤进数值计算模型,通过计算获得了埋头弹高速冲击入膛过程中的弹带变形、弹丸运动、弹丸姿态和挤进阻力等变化规律,为分析埋头弹火炮膛内弹炮耦合力学机理、优化埋头弹火炮的内膛结构提供了理论支撑。
1 埋头弹火炮内弹道物理和数学模型
1.1 埋头弹内弹道建模
本文以某40 mm 口径埋头弹火炮作为对象,图1 展示了内弹道时期的物理过程。当底火被击发后产生高温燃气瞬间点燃点火药,点火药燃烧产生的压力作用于弹丸底部,推动弹丸克服拔弹力并沿着可燃导向筒自由加速,直至弹带与坡膛发生高速碰撞。此时可燃导向筒受压破裂,主装药被全面点燃。火药燃气继续推动弹丸挤进膛线,完全挤进后弹带上形成与膛线结构吻合的刻槽,此后的膛内运动和传统火炮相同,弹丸建立稳定的旋转状态,并在膛内加速运动至出炮口。

图1 埋头弹火炮内弹道物理模型Fig. 1 Physical model of interior ballistics of the CTA gun
将埋头弹的内弹道物理过程分为两个阶段进行数学建模。第一阶段为点火药的燃烧作用期,建立如下第一阶段的内弹道方程组。
点火药的形状函数:
式中:ψb为点火药的已燃百分比;χb和λb为点火药形状特征量;Zb为点火药已燃相对厚度。
点火药的燃速方程:
式中:u1b、nb和e1b分别为点火药的燃速系数,燃速指数和弧厚;p为弹后空间平均压力。
弹丸在导向筒内的运动方程:
式中:φ1为弹丸在导向筒内运动时的次要功系数;m为弹丸质量;v为弹丸运动速度;S1为弹丸最大横截面积。
弹丸速度与行程关系式:
式中:l为弹丸运动位移。
火药燃气状态方程:
式中:lψb、l0b和V0b分别为第1 阶段的药室自由容积缩颈长、药室容积缩径长和药室容积;ωb、Δb、αb、ρb分别为点火药的装药量、装填密度、余容、密度;R为气体常数;T为膛内气体平均 温度。
膛内能量守恒方程:
式中:Tb为点火药的爆温;θ=k- 1,k为比热比。
由式(5)和式(7),可得内弹道第一阶段的基本方程
式中:fb为点火药的火药力,fb=RTb。
第一阶段计算的初始条件为
式中:pbs为点火压力;ψ0b为点火药的初始已燃百分比;z0b为点火药初始已燃相对厚度。
求解式(1)~式(9),可获得第一阶段的内弹道变化规律。
第2 阶段为主火药、未燃烧完的点火药和可燃导向筒的共同作用期。将第一阶段相关内弹道参量的终值作为第2 阶段内弹道参量的初值,主装药、可燃导向筒各内弹道参量的含义和点火药的相同,将参量符号下标由b 改为z 和c 即可。建立第2 阶段的内弹道方程如下所示。
主火药、可燃导向筒和未燃烧完的速燃火药的形状函数为
燃速方程分别为
弹丸在身管内的运动方程为
式中:φ2为弹丸在身管内的次要功计算系数;S2为身管直膛段的最大横截面积;Fr为挤进阻力。
火药燃气状态方程为
式中:lψ、l0和V0分别为第一阶段药室自由容积缩颈长、药室容积缩径长和药室容积;ωi、Δi、αi、ρi分别为3 种装药的装药量、装填密度、余容、密度。
膛内能量守恒方程:
式中:Ti为3 种装药的爆温。
由式(13)和式(15),可得内弹道第2 阶段的基本方程为
式中:fi为3 种装药的火药力,fi=RTi。
求解式(4)、式(10)~式(16),可以得到第2 阶段的内弹道变化规律。
1.2 内弹道数值模拟
对某40 mm 口径埋头弹火炮的装药方案进行了常温药温下的内弹道数值模拟,装药参数如表1所示。对建立的内弹道控制方程组进行求解,内弹道数值求解程序图如图2 所示。
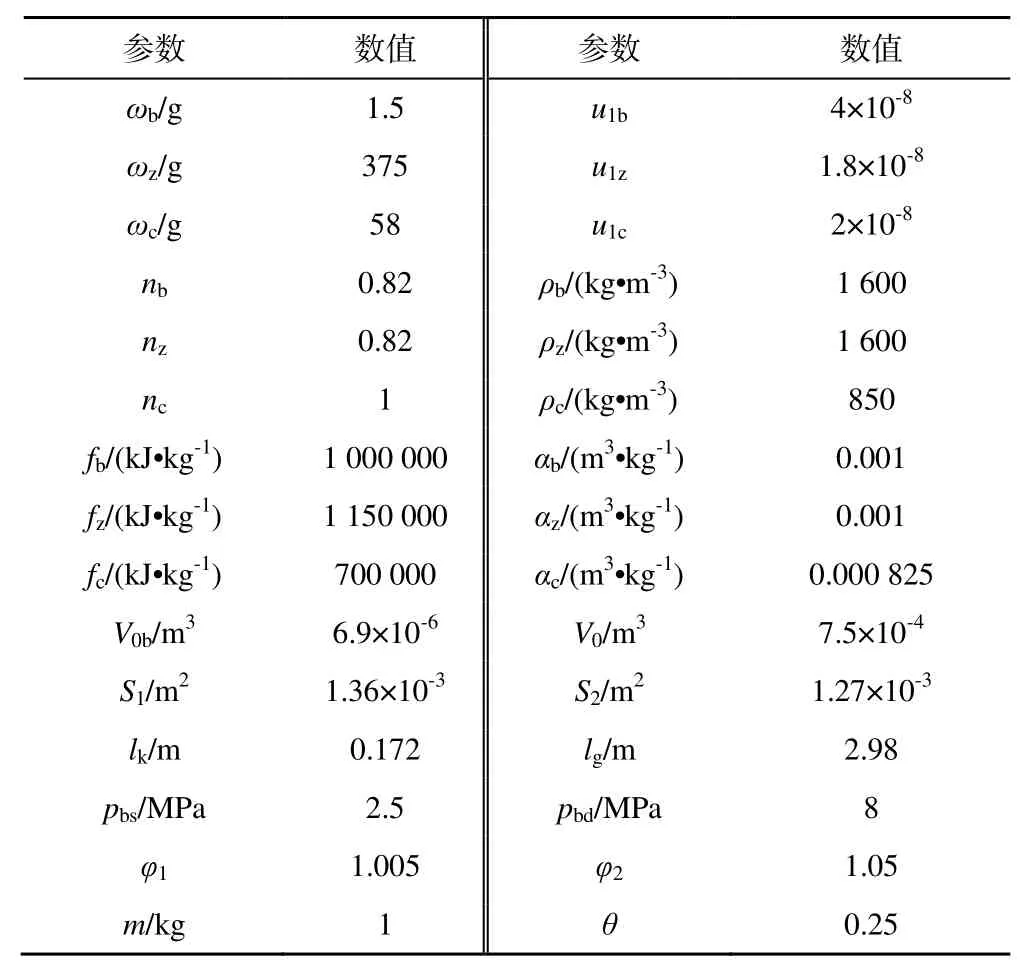
表1 埋头弹装药参数Table 1 Charge parameters of CTA
首先根据输入参数计算内弹道的常量和初值,然后利用第一阶段的控制方程对内弹道参数进行循环计算,当膛压上升至pbd,燃气压力对弹丸底部产生的推力足够克服拔弹力时,弹丸在导向筒内开始运动,直到弹带与坡膛接触为止,此时弹丸的运动位移为lk。当弹带与坡膛接触后,导向筒在膛压作用下发生破裂,利用第2 阶段的控制方程对内弹道参数进行循环计算,直至弹丸的弹带后端面与炮口端面重合,此时弹丸在膛内的运动行程为lg。最后输出内弹道参量随时间和弹丸位移的变化规律。
为验证内弹道理论模型的正确性,在弹道炮上对该装药方案进行了常温工况下的射击实验,并对射击后的弹丸进行了回收。测试了膛底压力和炮口的初速,根据文献[1]中所述的膛底压力和膛内平均压力的压力换算关系可求得平均膛压的变化曲线。将平均膛压换算曲线与数值计算结 果曲线进行对比,如图3 所示,实测压力曲线 与计算压力曲线可以较好地吻合,最大平均膛压计算值为347.16 MPa,最大平均膛压实测值为 341.19 MPa;炮口初速计算值1 123.7 m/s,炮口初速实测值为初速1 109.85 m/s。初速和最大膛压的相对误差分别为1.24%和1.72%。考虑到弹丸在膛内运动时火药燃气有一定的泄漏,说明所建立的内弹道模型准确合理,能够正确描述内弹道和参量的变化规律。

图3 平均膛压数值结果与实测值换算结果的对比Fig. 3 Comparison of the numerical results of the average bore pressure with the conversion results of the measured values
由于弹丸卡膛时刻的速度测量非常困难,本文通过数值计算获得弹丸入膛初始时刻的瞬时速度,并将其作为挤进过程的速度边界条件。弹丸的膛内运动速度和位移变化规律如图4 所示,弹带与坡膛接触的时刻为8.41 ms(B点),此时刻对应的弹丸速度vk为78.2 m/s(A点)。根据文献[1]中的弹底压力和平均膛压的换算关系式计算弹底压力pd,将弹底压力的曲线在8.41 ms 时刻截断,以此时刻之后的弹底压力pd和弹丸速度vk作为高速冲击入膛过程计算的边界条件。
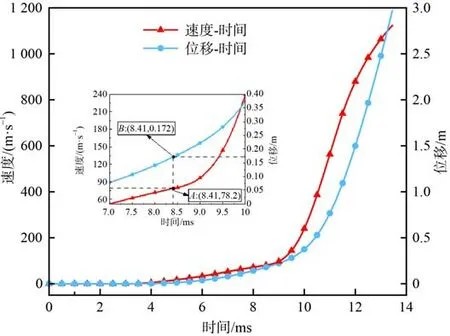
图4 弹丸速度-时间、位移-时间曲线Fig. 4 Velocity-time and displacement-time curves of the projectile
2 高速冲击挤进模型
2.1 弹丸姿态定义
受弹带的塑性大变形和接触碰撞的影响,弹丸的姿态会在挤进时期发生剧烈变化,弹丸的摆动角过大会造成弹丸在膛内发生章动的现象,影响弹丸在全深膛线内的运动状态,从而对射击精度产生综合影响。
为了揭示埋头弹挤进过程中的姿态变化规律,本文建立了相关坐标系来描述弹丸的运动姿态。弹体坐标系Ocx0y0z0的原点Oc位于弹丸的质心处,Ocx0轴平行于身管轴线,Ocy0轴与地面相垂直向上,Ocz0轴遵循右手螺旋法则。弹丸质心平动坐标系Ocξηζ的原点与弹体坐标系相同,Ocξ轴和弹丸轴线重合,Ocη轴与Ocy0轴位于同一个垂面内,指向上方,Ocζ轴遵循右手螺旋法则。
其中弹丸质心平动坐标系Ocξηζ与弹体固连,随弹丸平动而不绕弹轴旋转,弹体坐标系Ocx0y0z0先绕着Ocz0轴旋转角度φ1,再绕Ocy0轴旋转角度-φ2,得到弹丸质心平动坐标系Ocξηζ。φ1、φ2分别为弹丸的纵、横向摆动角,于是弹丸姿态角可以表示为Φ=φ1+φ2i,弹丸姿态示意图如图5所示。
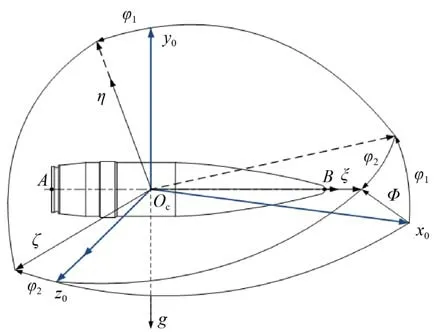
图5 弹丸姿态示意图Fig. 5 Schematic diagram of projectile attitude
计算时输出弹轴上两点A、B的距离ld以及挤进时每一瞬时的的运动状态,假设弹体和身管为刚体,根据绝对坐标系下A、B两点在的位移uA、uB和速度vA、vB,可以计算得到弹轴的方向矢量nd及摆动速度,继而算得弹丸轴线的摆动角φ1、φ2及摆动角速度。
弹轴的方向矢量的分量:
式中:uAx、uAy、uAz、uBx、uBy、uBz分别为绝对坐标系下A、B两点的位移在3 个轴向上的分量。
摆动速度矢量的分量:
式中:vAx、vAy、vAz、vBx、vBy、vBz分别为绝对坐标系下A、B两点速度在3 个轴向上的分量。
由此可求得摆角与摆角速度:
2.2 冲击入膛过程弹带受力分析
在高速冲击挤进入膛的过程中,弹带受到坡膛、膛线的作用产生塑性大变形,弹带受力示意图如图6 所示。图6 中,α为坡膛锥角,β为膛线缠角,Fτg、Fτl、Fτc、Fτd、Fτu分别为膛线阴线、阳线、坡膛、导转侧、非导转侧挤压弹带的切向力,Fng、Fnl、Fnc、Fnd、Fnu分别为膛线阴线、阳线、坡膛、导转侧、非导转侧挤压弹带的法向力。
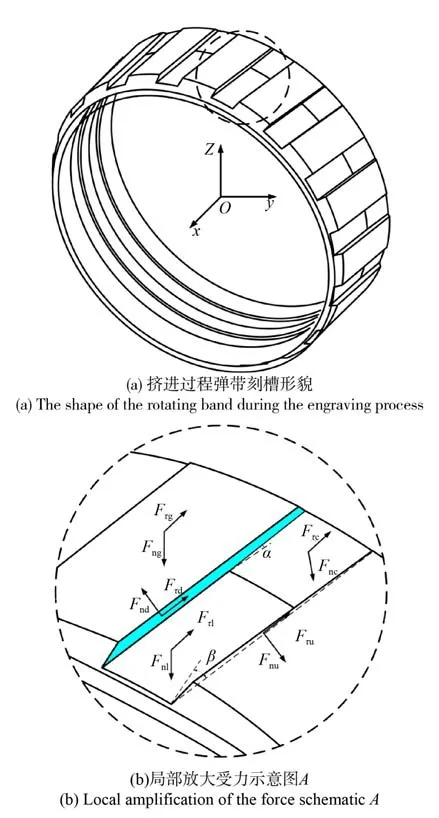
图6 挤进过程弹带的形貌和受力示意图Fig. 6 Schematic diagram of the shape of and force on the rotating band during the engraving process
则弹丸所受总的力为
式中:Fg、Fl、Fc、Fd、Fu分别为膛线阴线、膛线阴线、阳线、坡膛、导转侧、非导转侧挤压弹带的力。记各接触面面积分别为Sg、Sl、Sc、Sd、Su,则弹带在各个接触面的受力由法向应力σ和切向应力τ来表示。
式中:S表示弹带与内膛各接触面的接触面积。
身管轴向的弹带受力为
式中:n为膛线条数。
身管周向的弹带受力为
2.3 冲击挤进有限元建模
以某40 mm 埋头弹火炮为研究对象,弹带的高速冲击挤进入膛过程如图7 所示。初始时刻弹丸以入膛速度vk与坡膛碰撞,然后在弹底压力的作用下,克服挤进阻力沿身管轴向前进,直至弹带完全挤入全深膛线为止。
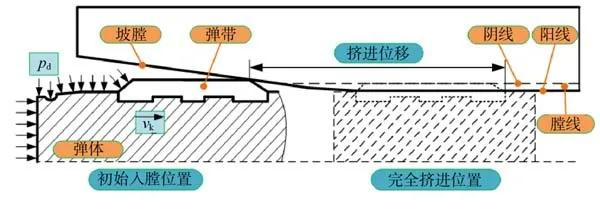
图7 高速冲击挤进入膛过程示意图Fig. 7 Schematic diagram of the high-speed impact engraving process
建立包含身管、弹体和弹带的精细化六面体网格模型,挤进过程完成前弹丸的圆柱部能够被可靠约束在身管内,以确保能准确描述挤进过程弹丸的运动特性。如图8 所示,整个有限元计算模型包含有920 538 个单元。忽略次要因素的影响,对挤进过程作如下假设:
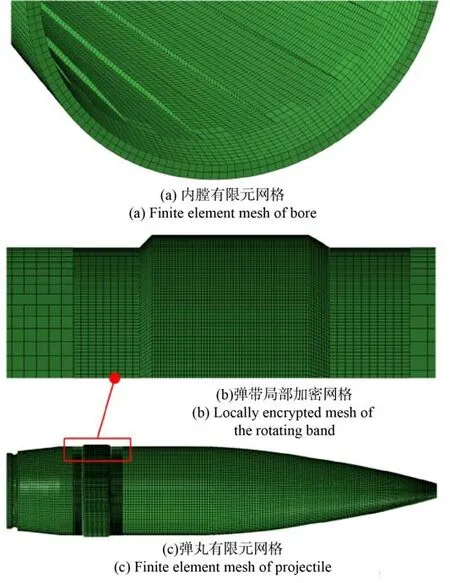
图8 挤进系统有限元网格Fig. 8 Finite element meshes of the engraving system
1)将弹体和身管看作刚体,挤进过程为绝热过程;
2)忽略弹丸的动不平衡,将弹丸内部炸药的质量等效至弹体,假定初始时刻弹丸与身管同轴;
3)挤进过程身管固定,忽略弹丸前部的空气阻力和激波的影响。
与发射传统弹药的火炮相比,埋头弹高速冲击入膛过程中的弹带变形有明显不同:
1)弹带在更高的应变率条件下产生大变形,高加载速度下的应变率效应和热效应对挤进过程具有关键作用[27];
2)伴随高温、高压和高速,接触界面的摩擦系数从挤进开始便会显著减小。
采用Lagrange 有限元法计算高速冲击挤进过程会出现严重的网格畸变,导致计算中断,为此,本文采用FEM-SPH 耦合算法,耦合示意图如图9所示。为精确控制弹带SPH 粒子的分布,在有限元建模时所有求解域都采用基于Lagrange 有限元法的网格划分,计算开始时弹带节点被转化为SPH 粒子。弹带的网格模型及SPH 粒子模型如 图10 所示。

图9 SPH 质点与Lagrange 网格的耦合示意图Fig. 9 Coupling diagram of SPH particles and Lagrange grids
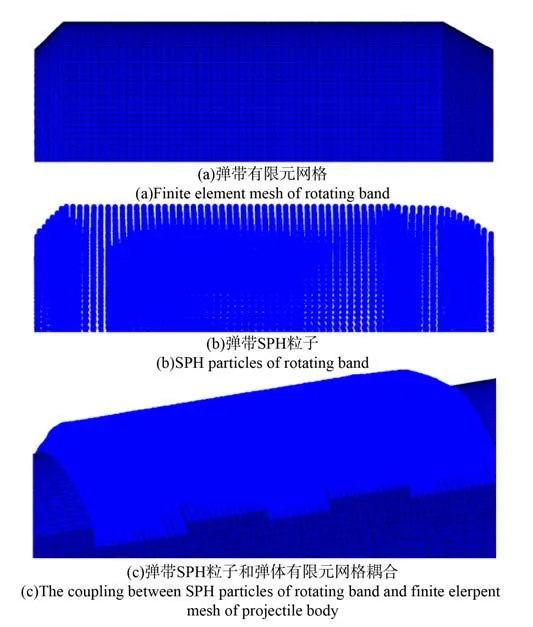
图10 弹带的网格和SPH 粒子Fig. 10 Meshes and SPH particles of the rotating band
对冲击入膛挤进过程进行显式求解,减缩积分引起的零能沙漏模态采用沙漏算法进行抑制。
2.4 弹带材料模型
在埋头弹高速冲击入膛过程中,弹带会历经弹塑性变形和损伤失效,最终发生韧性断裂,涉及到弹带材料的应变硬化、应变率硬化和温度软化。本文采用Johnson-Cook 模型[28]来描述弹带材料的塑性本构关系,本文弹带材料为紫铜,弹带材料本构方程的相关参数如表2 所示。
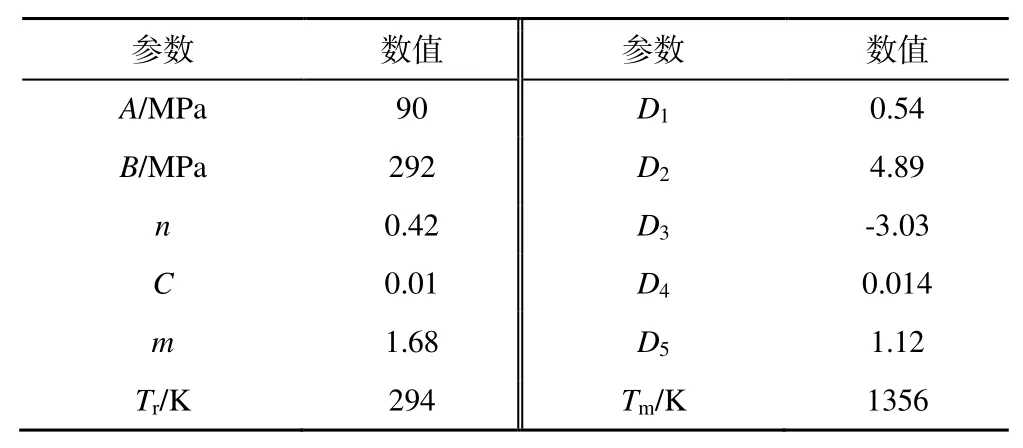
表2 弹带材料模型参数Table 2 Material parameters of the rotating band
材料的失效由以下准则进行判断:
式中:D表示损伤参数,即当D累计到1 时,材料断裂;表示有效塑性应变增量;εf为弹带材料的断裂应变。
2.5 接触及摩擦
本文采用FEM-SPH 耦合算法进行埋头弹高速冲击挤进过程的数值计算,应考虑以下接触耦合 问题[11]:
1)弹带与身管内膛界面间的接触-碰撞问题。定义弹带SPH 粒子为从节点,接触-碰撞界面上的身管表面定义为主面,图11 所示为接触耦合算法的示意图。采用点面接触的接触方式,通过罚函数形式将质点的力作用于单元表面。
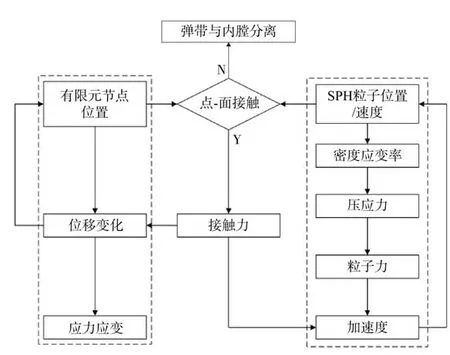
图11 SPH-FEM 接触耦合算法Fig. 11 SPH-FEM coupling contact algorithm
2)弹带与弹体接触部位的固连接触问题。定义弹带SPH 粒子为从节点,接触界面的弹体表面定义为主表面,当从节点与对应的主表面间出现微小距离时,采用正交投影法将从节点移动到主表面,以确保可靠固连接触。
式中:µd为摩擦系数;σf′为动态流动应力;v′为相对滑动速度。
周彦煌等[29]利用美军针对弹带材料所做的高速高压摩擦实验所测得的数据,将摩擦系数µd拟合为与动态流动应力和相对滑动速度v′的乘积相关的表达式。由式(28)中可见,随着动态流动应力和滑动速度的增加,弹带与身管之间的摩擦系数由0.4 降至0.021,这个拟合结果与Stiffler 等[30]根据流体动力学计算所得的弹带材料熔化液膜摩擦系数0.026 非常相近。考虑到埋头弹挤进的速度及紫铜材料的动态流动应力,基于库伦摩擦模型,设定动摩擦系数为0.021。弹体和身管之间的接触碰撞属于钢-钢之间的接触碰撞,设定动摩擦系数为0.2。
3 高速挤进数值模拟与分析
3.1 弹带变形分析
考察挤进过程中的弹带变形情况,弹带等效塑性应变云图如图12 所示。从图12 中可以看出:随着弹丸不断挤进,坡膛内径减小,弹带逐渐产生塑性变形,完全挤进后,弹带被膛线切割成槽;弹带与坡膛高速碰撞后迅速挤进,在0.5 ms 时刻时已完成绝大部分的挤进,而0.5~2 ms 之间时弹丸挤进缓慢接近停滞;2 ms 后,弹带挤进加速,直到2.65 ms 时刻弹带完全挤进。

图12 弹带塑性变形过程Fig. 12 Plastic deformation process of the rotating band
将射击实验回收的弹丸与有限元数值计算结果进行对比,如图13 所示。由图13 可以看出,有限元计算所得的弹带表面形貌和实际射击结果一致性较好,说明本文建立的高速冲击挤进有限元模型可以准确地刻画挤进过程弹带的变形情况。
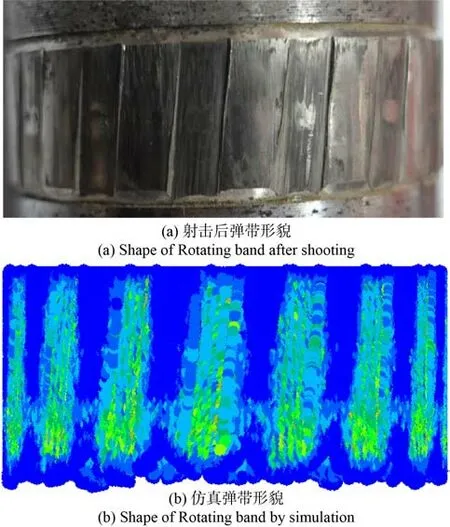
图13 试验和仿真得到的弹带形貌对比Fig. 13 Comparison of the shape of the rotating band obtained from the test and simulation
在弹带上分别选取典型部位的SPH 粒子,如图14 所示。其中:1 号、2 号、3 号、4 号粒子分别位于弹带上与阳线、阴线、阳线导转侧、阳线非导转侧相接触的部位;5 号粒子为受膛线挤压和剪切作用流动到弹带后方的粒子。考察各点的温度以及von Mises 等效应力的变化规律。
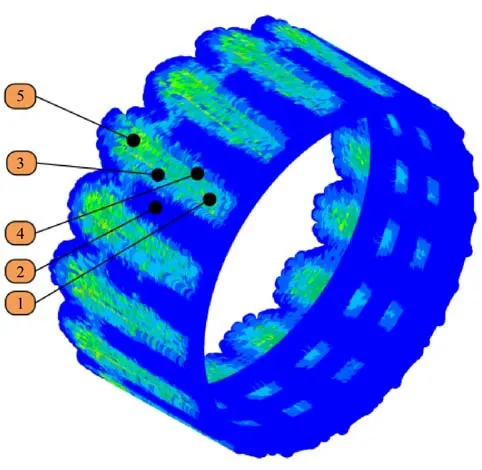
图14 弹带典型部位SPH 粒子Fig. 14 SPH particles in typical parts of the rotating band
高速冲击入膛过程中弹带与内膛表面会发生高压高速摩擦,从而产生大量的摩擦热,导致弹带的表面温度迅速上升。图15 表示了弹带表面典型部位在挤进过程中的温度变化规律。由图15 可见,随着弹带逐渐挤进,弹带表面的温度迅速且持续升高,挤进结束时弹带表面温度最高为1 293 K,其中弹带与阳线接触表面温度(1 241 K)高于与阴线接触表面的温度(790 K),弹带与阳线导转侧接触表面(3 号粒子)的温度略高于与阳线非导转侧接触表面的温度(4 号粒子)。由于弹带表面温度低于材料熔点,弹带表面未发生熔融。
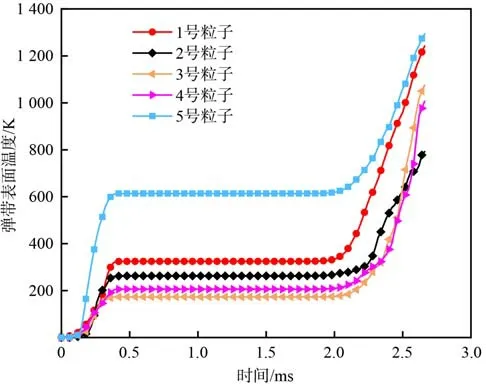
图15 弹带表面典型部位的温度Fig. 15 Temperature of typical parts of the rotating band surface
图16 表示了所选的弹带SPH 粒子的Mises 等效应力变化规律。从图16 中可以看出:弹带与膛线阴线和阳线之间的接触区域应力的变化规律基本一致,挤进过程应力的最大值约为575 MPa;初始时刻弹带与坡膛高速碰撞,应力值迅速升高,随着弹丸减速,弹带变形减缓,应力随之降低;当弹丸重新加速时,弹带的变形应变率增大,应力又迅速升高。完成挤进时弹带所受膛线的作用显著减小,等效卸载现象明显。
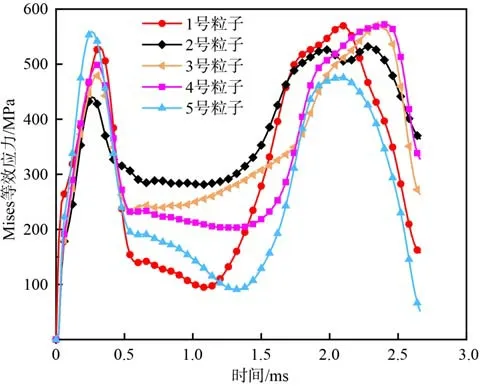
图16 弹带表面典型部位的等效应力Fig. 16 Equivalent stress of typical parts of the rotating band surface
弹带与阴线接触表面的应力略低于与阳线接触表面的应力,弹带与膛线的导转侧和非导转侧接触表面的应力基本相同。
3.2 挤进过程弹丸运动规律分析
图17 和图18 分别显示了挤进过程中弹丸速度及加速度随时间的变化规律。由图17 和图18 可以看出:埋头弹的挤进过程存在明显的分段特征,整个过程可分为减速挤进和加速挤进两部分,在减速挤进和加速挤进阶段中间时弹丸处于近乎静止状态;弹丸首先以高速撞击坡膛,受弹带变形阻力和摩擦阻力的影响,速度迅速减小,弹丸的初始动能转化为塑性变形能和摩擦耗散能,约0.5 ms 时速度减为0 m/s,在2 ms 左右时,随着膛压上升至足够克服材料的变形和摩擦阻力,弹丸速度快速上升,完全挤进时的弹丸速度为73.92 m/s。

图17 挤进速度-时间曲线Fig. 17 Velocity-time curve of engraving

图18 挤进加速度-时间曲线Fig. 18 Acceleration-time curve of engraving
图19 给出了挤进过程中的弹底压力做功、弹丸动能、摩擦耗散能及弹带变形能的变化趋势。由图19 可以看出,在减速挤进阶段弹丸的初始动能和弹底压力做功大部分都转化为了摩擦耗散能和弹带变形能。加速挤进阶段弹丸动能、弹带变形能迅速增加,摩擦耗散能也有所增加,弹底压力做功主要转换为弹丸动能、弹带变形能。在挤进结束时,弹丸动能约占弹底压力做功的45.5%。
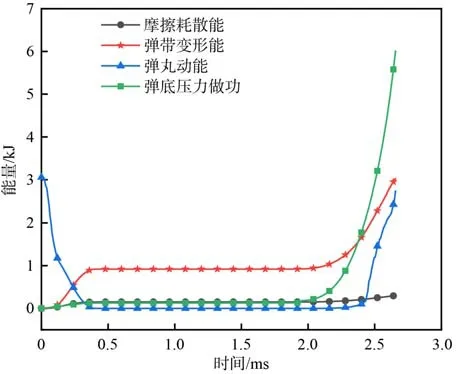
图19 挤进过程中的能量变化规律Fig. 19 Energy variation during the engraving process
根据2.1 节的理论分析,提取仿真计算有限元仿真结果进行弹丸姿态的解算,得到挤进过程中弹丸轴线的摆角及摆角速度,分别如图20 和图21 所示。由图20 和图21 可以看出;在减速挤进阶段,由于弹丸的速度较高,弹带与身管坡膛之间存在严重的动态冲击,随着不断挤进,弹丸不断受坡膛作用完成定位对中,弹丸姿态发生周期性的变化,摆动角幅度不断下降;弹丸加速挤进时,由于此时弹丸存在一定的初始摆动角,在迅速上升的弹底压力和轴向速度作用下,加剧了弹丸的摆动,横向和纵向的摆动角均快速增大;挤进即将结束时,弹丸运动趋于平稳,摆动角呈现出减小的趋势。
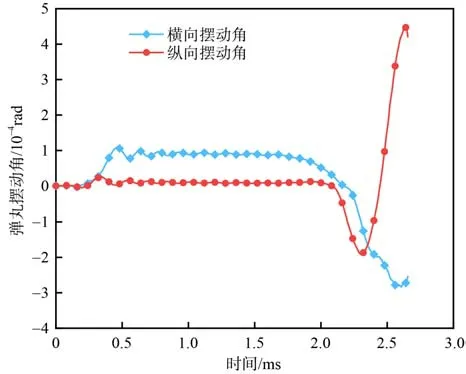
图20 弹丸横向摆动角和纵向摆动角Fig. 20 Lateral and longitudinal osllication angles of the projectile
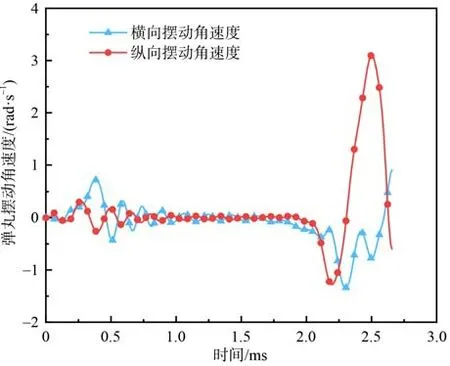
图21 弹丸横向摆动角速度和纵向摆动角速度Fig. 21 Angular velocity of transverse and longitudinal oscillation of the projectile
3.3 挤进阻力变化规律
根据2.2 节的弹带受力分析可知,受坡膛和膛线对弹带表面的挤压作用,各接触面上产生的法向载荷和切向摩擦力在炮膛轴线方向的分量之和即为挤进阻力。本文利用建立的高速冲击挤进模型计算获得了埋头弹高速冲击挤进阻力变化规律,同时为了充分展现埋头弹相较于常规弹丸在挤进过程中的特殊性,根据本文建立的挤进有限元模型,将弹丸挤进初始速度设为0 m/s,其余初始条件和边界条件保持不变,对弹丸进行了静态挤进数值计算,获得了静态挤进阻力的变化规律。将静态挤进和高速冲击挤进阻力规律进行对比,如图22 所示。

图22 动态挤进阻力变化规律Fig. 22 Resistance variation law of dynamic engraving resistance
分析图22 可知,弹带与坡膛高速碰撞后,挤进阻力迅速上升,这是因为弹带材料发生了高应变率的塑性大变形,迅速上升的阻力导致弹丸速度迅速减小。随着弹丸速度减小,弹带变形的应变率降低,挤进阻力迅速减小至19 kN。随着膛压不断升高,推动弹丸再次加速运动,由于此时弹带未变形宽度和面积减少,且弹带表面温度较高,材料软化会导致摩擦系数减小,弹带挤进阻力升至31.5 kN后开始缓慢下降,即将挤进完成时阻力迅速降低并稳定在10 kN 左右。埋头弹高速冲击挤进阻力变化规律呈现出两次“上升-下降”过程,整个挤进过程的阻力峰值为95.288 kN。
静态挤进过程中随着弹带挤进,挤进阻力持续上升,上升速度相较于高速冲击挤进模型比较缓慢,阻力至最大值后随着挤进深度的增加开始迅速下降,挤进即将结束时,挤进阻力缓慢下降并像高速冲击挤进模型一样稳定在10 kN 左右。这是因为挤进完成后弹带形成与膛线吻合的刻槽,此时挤进阻力仅源自于弹带和膛线之间的摩擦阻力,两个模型的挤进终了阻力稳定值较为一致。静态挤进阻力峰值为82.27 kN,低于高速冲击挤进阻力峰值,从而说明高速冲击挤进模型与静态挤进模型的挤进阻力变化规律存在着很大不同。
4 结论
本文通过分析埋头弹火炮的内弹道物理过程,建立了埋头弹火炮的零维内弹道数学模型,通过数值计算和射击实验验证了内弹道模型的准确性,考虑挤进过程中弹炮系统的摩擦和接触特性,将数值计算结果作为挤进过程的运动边界条件,采用FEM-SPH 耦合算法建立了高速冲击挤进过程有限元模型,研究了埋头弹高速冲击挤进入膛过程中的弹带变形、弹丸运动、弹丸姿态和挤进阻力等变化规律。得出以下主要结论:
1)建立的内弹道模型可以较为准确的描述弹丸在膛内的运动规律,通过内弹道计算得到的初始挤进速度为78.2 m/s。
2)埋头弹的冲击挤进过程呈现明显的分段特征,可分为减速挤进和加速挤进两段,在减速挤进和加速挤进中间弹丸接近于静止状态。挤进过程用时2.65 ms,挤进结束弹丸速度为73.92 m/s。大变形和高速摩擦会导致产生大量的热量,使得弹带表面接近材料熔点温度。
3)高速冲击挤进对弹丸的空间姿态产生很大的影响,减速挤进过程中弹丸姿态发生周期性的变化,摆动角幅值不断下降,加速挤进过程,摆动角迅速增大,挤进即将结束时,摆动角呈现出减小的趋势。
4)埋头弹的高速冲击挤进过程与静态或准静态挤进模型区别明显,挤进过程中的动态阻力呈现出两次“上升-下降”过程,最大挤进阻力95.288 kN,完全挤进时阻力降低并稳定在10 kN 左右。
