身管膛线类型及其动力学影响研究*

王宝元， 许耀峰， 周发明， 刘 军， 衡 刚

(西北机电工程研究所， 陕西 咸阳 712099)

身管膛线类型及其动力学影响研究*

王宝元， 许耀峰， 周发明， 刘 军， 衡 刚

(西北机电工程研究所， 陕西 咸阳 712099)

为了比较火炮身管等齐膛线、 渐速膛线和混合膛线之间的动力学响应差异， 采用动力学分析方法分析了身管膛线导转侧力、 膛线约束下的弹丸轴向加速度， 以及不同身管膛线条件下的炮口振动响应的变化规律. 结果表明， 在弹丸出炮口位置附近， 等齐膛线导转侧力最小， 渐速膛线导转侧力最大； 等齐膛线导转侧力曲线光滑， 而混合膛线导转侧力变化剧烈、 曲线载荷梯度非常大； 当弹头刚露出炮口时， 混合膛线导转侧力突变范围达3倍之多， 混合膛线约束下的弹丸轴向加速度在炮口附近有突跳； 与等齐膛线相比， 混合膛线引起的炮口绕身管轴线转动角速度和角加速度分别增加了92.7%和367.5%. 等齐膛线有利于弹丸膛内平稳运动， 有利于减小炮口振动响应.

火炮； 身管； 膛线； 导转侧力； 炮口振动

0 引 言

炮口振动响应是影响火炮射击密集度的关键因素之一， 较小的炮口振动响应是实现火炮射击密集度高性能的基本保证[1-2]. 影响炮口振动响应的因素复杂多样， 身管膛线特性就是其中的一项重要影响因素.

火炮身管结构内表面有膛线. 膛线是指在炮膛导向部管壁上与身管轴线成一定斜角的若干条螺旋形的凸起和凹槽， 其作用是赋予弹丸在出炮口时一定的旋转速度， 以保证弹丸在空中飞行的稳定性. 螺旋槽凸起的部分称为阳线， 凹下的槽部称为阴线. 阳线有一个侧面与弹带上相应处紧贴， 赋予弹丸一定的旋转力， 此侧面称为导转侧.

为了改善膛线的受力状况或改善弹丸在膛内运动的闭气性能， 因而出现了各种类型的膛线. 根据缠角α沿炮膛轴线变化规律的不同， 可分为等齐膛线、 渐速膛线和混合膛线三种. 等齐膛线的缠角α沿炮膛轴线始终为一常数； 渐速膛线的缠角α沿炮膛轴线变化， 为减小磨损， 缠角起始处的缠角很小， 向炮口方向缠角逐渐增大； 混合膛线常由渐速膛线和等齐膛线组成， 一般前段为渐速膛线， 后段为等齐膛线.

火炮发射时， 膛内火药燃气在推动弹丸沿炮膛轴线运动的同时， 弹带切入膛线， 在弹带上刻出了与膛线相对应的凹槽和凸起. 膛线的导转侧与弹带上的凹槽的一边紧贴， 存在着相互作用的正压力N， 该正压力定义为膛线导转侧力. 因此， 沿弹带的圆周均匀分布着同一旋向的作用力， 迫使弹丸绕自身轴线旋转[3].

膛线导转侧力大小和变化规律对火炮射击密集度有重要影响. 膛线导转侧力幅值小、 变化波动小， 有利于火炮射击密集度的提高； 反之， 膛线导转侧力幅值大、 变化波动大， 则不利于火炮射击密集度的提高， 会使火炮射击密集度变差， 减小火炮威力.

多年来， 人们十分重视火炮身管膛线相关特性的研究. 文献[4]研究了内弹道过程中压力拟合及身管受力分析问题， 分析了导转侧弹丸受力， 推导了弹丸受力与弹底压力的关系式， 计算了等齐膛线导转侧力数值. 文献[5]利用有限元和接触动力学理论对末制导炮弹膛内过载问题、 动态强度及减旋等开展研究， 对末制导炮弹在膛内所受的火药气体压力、 惯性力、 弹带压力、 不均衡力、 导转侧力和摩擦力等进行了分析与计算， 给出了等齐膛线导转侧力计算曲线. 文献[6]根据身管内膛实际磨损规律， 在拟订了膛线导转侧最佳受力方案的基础上， 建立了与其相对应的混合膛线的设计方法. 为了改善火炮阳线导转侧的受力， 提高炮身寿命， 文献[7]提出了将制式火炮的矩形膛线改进为锯齿形膛线的结构， 并结合某榴弹炮从理论上对这两种膛线结构的受力进行了对比计算. 文献[8]利用身管等齐膛线的缠角值沿炮膛轴线始终为一常数的原理， 在炮膛纵向展开的平面图上， 采用三角函数换算关系， 提出了等齐膛线缠角的简易检测方法， 并在实践中应用. 文献[9]为了研究弹丸膛内运动特性， 建立了弹丸身管耦合系统有限元模型， 发现了弹带与膛线的作用对弹丸速度具有一定的影响. 文献[10]基于动态非线性有限元方法， 建立了弹丸身管耦合系统非线性有限元分析模型， 开展了火炮身管阳线损伤机理分析. 本文主要开展等齐膛线、 渐速膛线和混合膛线三种膛线比较研究， 不同类型膛线影响炮口振动响应研究和不同类型膛线约束下的弹丸轴向加速度特性研究， 为进行火炮身管不同类型膛线影响射击密集度分析提供参考.

1 膛线导转侧力

将炮膛纵向展开成平面， 等齐膛线、 渐速膛线和混合膛线三种类型膛线见图 1 所示. 其中，α0是等齐膛线缠角，α1和α2分别是渐速膛线在起始点和终点的缠角，α3和α4分别是混合膛线在起始点和终点的缠角， 同时，α4也是混合膛线后段等齐膛线的缠角，lg为导向部的长度， 而l1和l2分别为混合膛线中沿身管轴线方向的渐速膛线长度和等齐膛线长度.

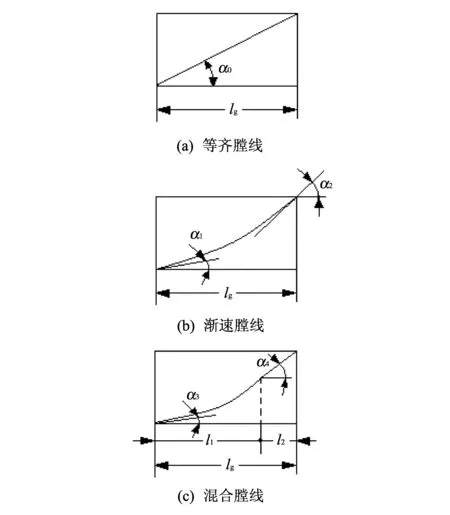
图 1 三种类型膛线展开图Fig.1 Sketch of three kinds of outspread rifling

以弹丸为自由体进行受力分析， 经过公式推导， 得到了膛线导转侧力公式为[3]

(1)

式中：n为膛线数；ρ为弹丸惯性半径；r为口径之半(d/2)；pd为弹底压力；S为导向部横剖面面积；α为缠角；m为弹丸质量；v为弹丸速度；x为沿身管轴线长度变量.

由式(1)可知， 膛线导转侧力N的大小与弹丸的速度、 结构、 弹底压力、 膛线缠角和条数等有关， 而弹底压力的变化又直接取决于膛压的变化，N的大小及其规律将直接影响火炮射击精度和身管寿命. 下面将分别给出等齐膛线、 渐速膛线和混合膛线导转侧力表达式.

1.1 等齐膛线

(2)

1.2 渐速膛线

如图 2 所示， 设渐速膛线为二次抛物线， 如o, 1, 2点所在的曲线， 其方程式为

(3)

图 2 渐速膛线示意图Fig.2 Sketch of increasing rifling

式中：p为待定常数， 根据边界条件可以确定. 在图 2 中，o点为抛物线顶点， 1点和2点分别为渐速膛线起始点和终点，x1点和x2点为沿身管轴线方向上分别与1点, 2点对应的点， 取x1点和x2点之间沿身管轴线方向上距离为l，α1和α2分别为渐速膛线在起始点和终点的缠角. 方程式(3)对x求导数为

(4)

因为曲线一阶导数就是曲线在该点的斜率tanα， 因此， 式(4)变为

(5)

或

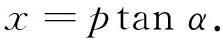
(6)

根据边界条件

(7)

将式(7)代入式(6)， 有

(8)

结合x1点和x2点之间沿身管轴线方向上距离l， 解方程组(8)， 有

(9)

这样， 渐速膛线二次抛物线为

(10)

式(10)对x求导数并整理后， 有

(11)

式(11)对x求导， 有

(12)

将式(11)和式(12)代入式(1)， 得渐速膛线导转侧力为

(13)

注意， 式(13)中的x取值范围从x1到x2. 式(13)与图 1(b) 相对应， 则l=lg.

同一门火炮身管膛线类型可以选择为等齐膛线、 渐速膛线或混合膛线. 不管选择哪一类型膛线， 为保持弹丸外弹道飞行稳定性， 弹丸炮口转速必须相同. 渐速膛线炮口缠角α2与炮口缠度ηg必须满足

(14)

1.3 混合膛线

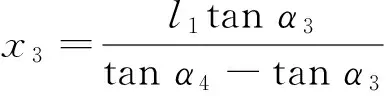
(15)

当x4≤x≤x4+l2时(即等齐膛线部分)， 混合膛线导转侧力为

(16)

以某火炮为例， 分3种工况计算身管膛线导转侧力： (a) 炮口点， (b) 最大弹底压力点， (c) 混合膛线中的前段渐速膛线与后段等齐膛线过渡点. 将上述3个特征点的弹底压力pd， 弹丸速度v， 弹丸行程x数值分别代入式(2)， 式(13)， 式(15)和式(16)， 则该火炮身管膛线导转侧力计算结果见表 1 所示， 图 3 是某火炮身管不同类型膛线导转侧力计算曲线， 其中，x0为长度比例系数. 结果表明， 在等齐膛线、 渐速膛线和混合膛线三种膛线中， 在弹丸出炮口位置附近， 等齐膛线导转侧力最小， 渐速膛线导转侧力最大； 等齐膛线导转侧力曲线光滑， 而混合膛线导转侧力变化剧烈、 曲线载荷梯度非常大； 当弹头刚露出炮口时， 混合膛线导转侧力是等齐膛线导转侧力的3倍之多， 随后， 混合膛线导转侧力由最大值9 314.26 N急速下降到等齐膛线导转侧力2 318.39 N 水平. 等齐膛线有利于减小炮口振动响应， 有利于火炮射击密集度性能提高.

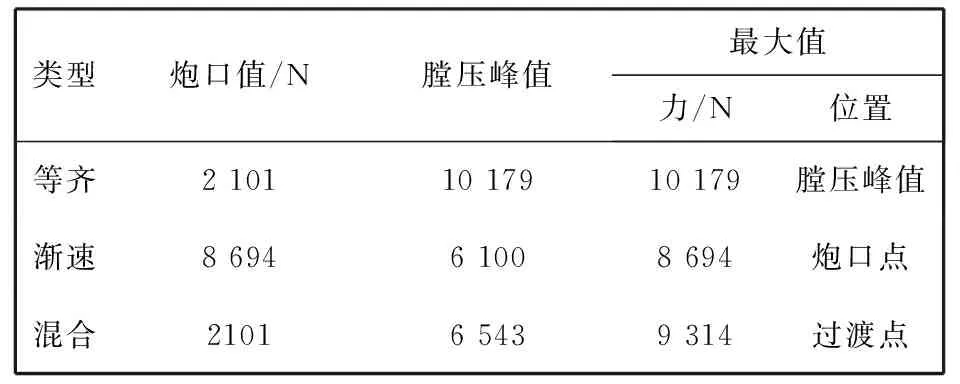
表 1 某火炮身管不同类型膛线导转侧力计算结果

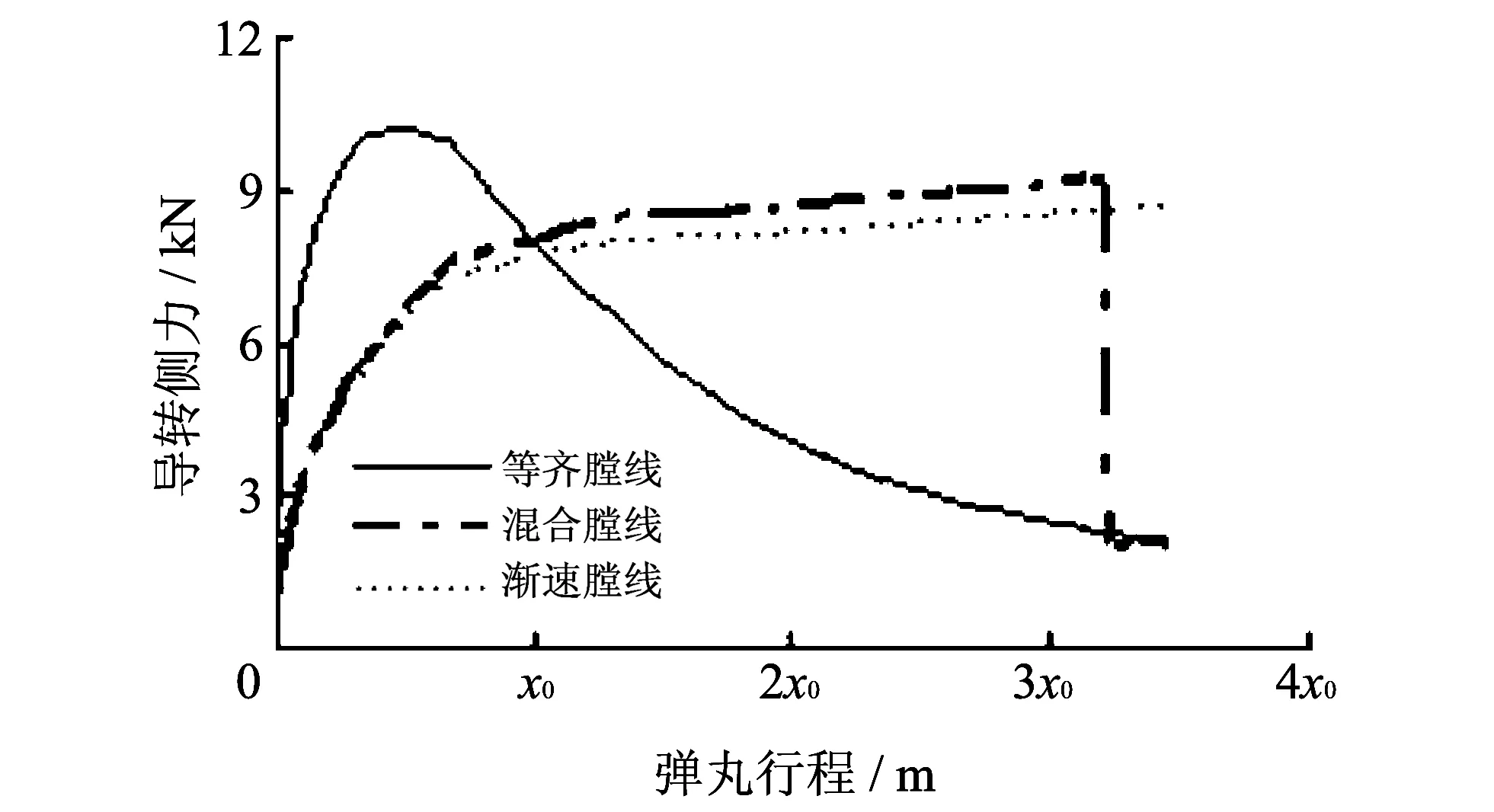
图 3 某火炮不同类型膛线导转侧力计算曲线Fig.3 Calculation curves of driving edge force of three kinds of rifling for a gun

以膛线为分析对象， 将膛线导转侧力分解为圆周方向和身管轴向， 图 4 是膛线导转侧受力示意图. 这样分解， 便于炮口振动响应计算时的激励力加载.

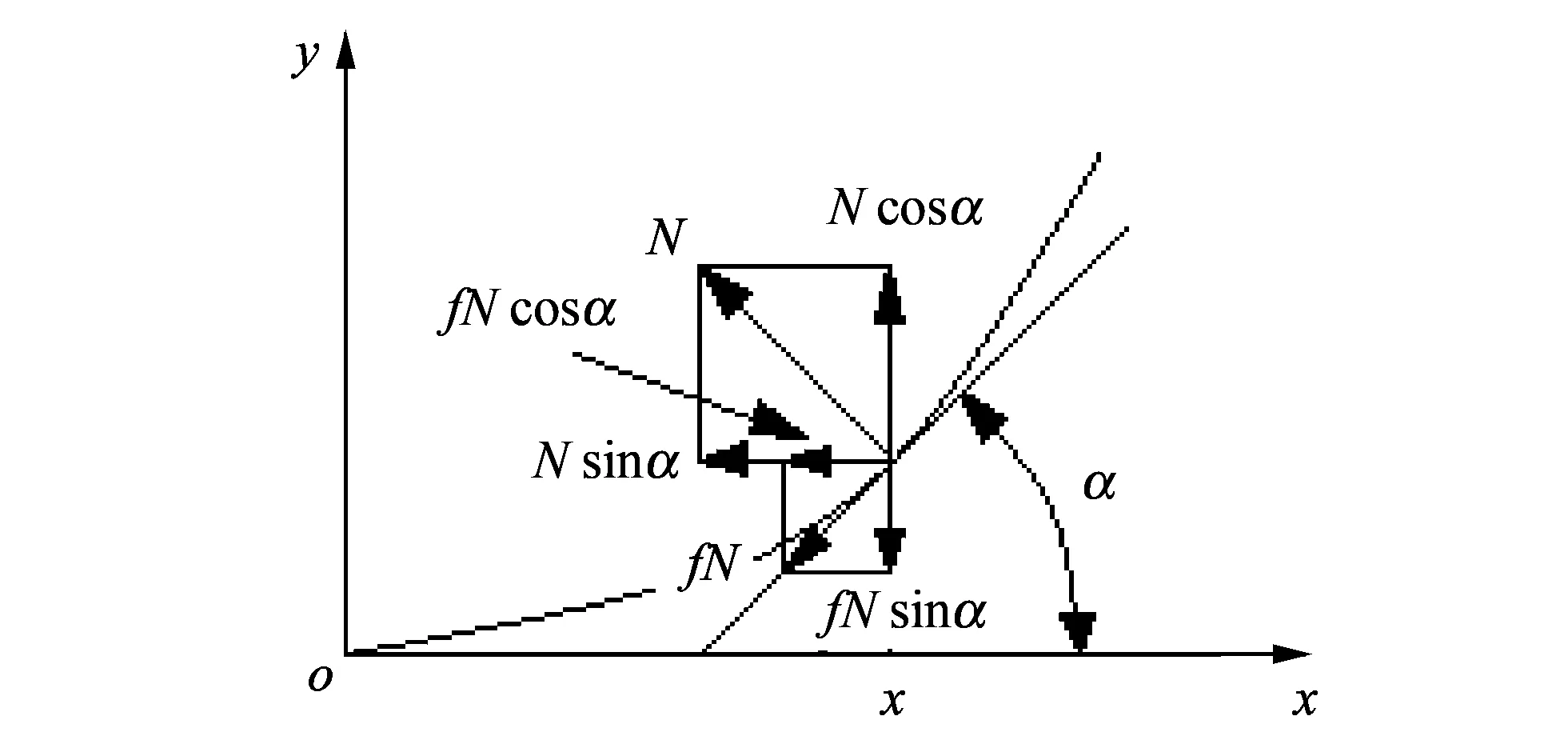
图 4 膛线导转侧受力示意图Fig.4 Sketch of driving edge force for rifling

圆周方向扭矩(从炮尾向炮口观察为逆时针)为

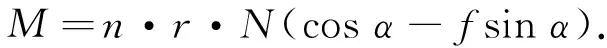
(17)

身管轴向力(从炮口指向炮尾)为

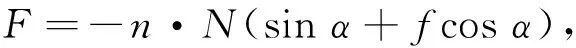
(18)

式中：f为摩擦系数， 金属与金属之间的摩擦系数一般在0.16～0.20范围内变化， 取f=0.18.

经过火炮系统动力学仿真模型响应计算， 在炮膛合力和膛线导转侧力共同作用下， 炮口绕身管轴线转动角速度和角加速度对比计算结果见图 5， 图 6 和表 2( 弹丸出炮口时刻)所示， 其中表示时间比例系数， 角速度负值表示炮口绕身管轴线转动角速度矢量从炮口指向炮尾.

理论研究表明[11]， 在角位移、 角速度和角加速度三个因素中， 角速度和角加速度是影响火炮射击密集度的关键因素. 结果表明， 与等齐膛线相比， 混合膛线引起的炮口绕身管轴线转动角速度和角加速度分别增加了92.7%和367.5%. 等齐膛线约束下的炮口绕身管轴线转动角速度和角加速度明显小于混合膛线. 等齐膛线约束下的炮口绕身管轴线转动角速度和角加速度时间曲线较平稳， 而混合膛线约束下的炮口绕身管轴线转动角速度和角加速度时间曲线变化很剧烈. 等齐膛线身管引起的弹丸起始扰动将会显著小于混合膛线身管.

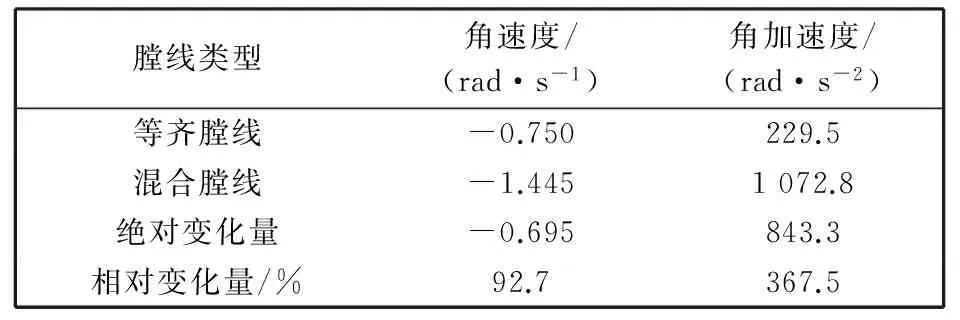
表 2 基于等齐膛线与混合膛线的炮口振动响应对比计算结果

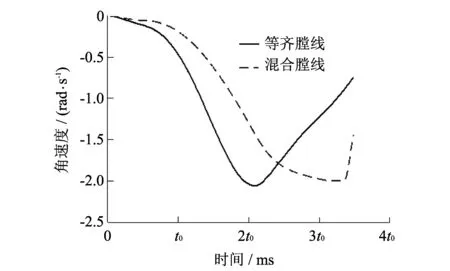
图 5 不同膛线角速度比较Fig.5 Angular velocity comparing by two kinds of rifling restriction

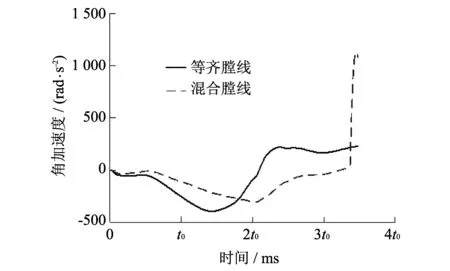
图 6 不同膛线角加速度比较Fig.6 Angular acceleration comparing by two kinds of rifling restriction

2 膛线约束下的弹丸轴向加速度

将炮膛纵向展开成平面， 沿身管轴向指向炮口为轴正向， 沿圆周展开方向为y轴， 建立坐标系oxy， 图 7 为坐标系oxy和身管膛线y=f(x)展开示意图. 下面分别给出弹丸在等齐膛线、 渐速膛线和混合膛线约束下沿身管轴向的加速度表达式.

图 7 坐标系oxy和膛线y=f(x)展开示意图Fig.7 Sketch of coordinate system oxy and outspread rifling y=f(x)

2.1 等齐膛线

对于膛线缠角为α0的等齐膛线， 其膛线展开方程式为

(19)

从式(19)中解出x， 则

(20)

式(20)对时间求导， 有

(21)

式(21)利用了角速度与圆周切线方向线速度关系， 注意口径之半r=d/2. 式(21)再对时间求导， 得

(22)

根据弹丸旋转方程式

(23)

有

(24)

将式(24)代入式(22)并整理后， 有等齐膛线约束下的弹丸轴向加速度为

(25)

2.2 渐速膛线

设渐速膛线为二次抛物线形式， 其方程式为

(26)

从式(26)解出变量x， 有

(27)

式(27)对时间求导数， 有

(28)

式(28)再对时间求导数， 有

(29)

同等齐膛线公式推导， 有渐速膛线约束下的弹丸轴向加速度

(30)

其中

(31)

2.3 混合膛线

设混合膛线前段为渐速膛线， 后段为等齐膛线. 利用上述等齐膛线和渐速膛线约束下的弹丸加速度表达式， 则混合膛线前段渐速膛线约束下的弹丸加速度表达式为

(32)

其中

(33)

混合膛线后段等齐膛线约束下的弹丸沿身管轴向加速度为

(34)

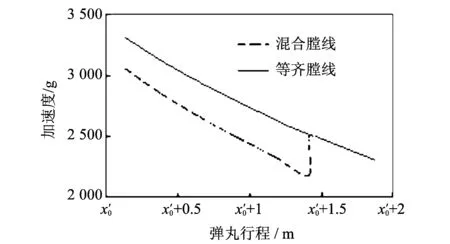
图 8 膛线约束下的弹丸轴向加速度Fig.8 Axial acceleration of projectile by rifling restriction

3 结 论

本文研究表明： 身管膛线类型不同， 其弹丸膛内运动规律和炮口振动规律就不同. 在等齐膛线、 渐速膛线和混合膛线三种膛线类型中， 在弹丸出炮口位置附近， 等齐膛线导转侧力最小， 渐速膛线导转侧力最大； 等齐膛线导转侧力曲线光滑， 而混合膛线导转侧力变化剧烈、 曲线载荷梯度非常大； 当弹头刚露出炮口时， 混合膛线导转侧力突变范围达3倍之多， 混合膛线约束下的弹丸轴向加速度在炮口附近有突跳. 与等齐膛线相比， 弹丸出炮口时刻混合膛线身管引起的炮口绕身管轴线转动角速度和角加速度分别增加了92.7% 和367.5%. 等齐膛线有利于弹丸膛内平稳运动， 有利于减小炮口振动响应， 有利于火炮射击密集度性能提高.

[1]王宝元， 董文祥， 邵小军， 等. 弹丸后效期时间和距离测量方法[J]. 兵工学报， 2013， 34(10)： 1329-1333. Wang Baoyuan, Dong Wenxiang， Shao Xiaojun， et al. A method for measuring the aftereffect duration and operating range of projectiles[J]. Acta Armamentarii, 2013, 34(10)： 1329-1333. (in Chinese)

[2]王宝元， 许耀峰， 周发明， 等. 炮口振动与立靶散布特性试验研究[J]. 振动与冲击， 2014， 33(8)： 83-87. Wang Baoyuan， Xu Yaofeng， Zhou Faming, et al. Effect of muzzle vibration on vertical target dispersion[J]. Journal of Vibration and Shock， 2014， 33(8)： 83-87. (in Chinese)

[3]谈乐斌， 张相炎， 管红根， 等. 火炮概论[M]. 北京： 北京理工大学出版社， 2005.

[4]严侃， 任斌， 王晟. 内弹道过程中压力拟合及身管受力分析[J]. 四川兵工学报， 2012， 33(7)： 23-26. Yan Kan， Ren Bin， Wang Cheng. Pressure fitting in interior ballistics process and tube force analysis[J]. Journal of Sichuan Ordnance, 2012， 33(7)： 23-26. (in Chinese)

[5]张振辉. 末制导炮弹与火炮身管相互耦合机理及适配性技术[D]. 南京： 南京理工大学, 2013.

[6]李强， 徐健. 一种混合膛线的优化设计方法[J]. 火炮发射与控制学报， 2004(4)： 40-43. Li Qiang, Xu Jian. An optimized design method of gun barrel variable rifling[J]. Journal of Gun Launch & Control, 2004(4)： 40-43. (in Chinese)

[7]薛百文， 常德顺， 贾玉峰. 锯齿形膛线在火炮上的应用[J]. 机械工程与自动化， 2011(4)： 184-185, 191. Xue Baiwen, Chang Deshun, Jia Yufeng. Application of zigzag rifling in artillery[J]. Mechanical Engineering & Automation， 2011(4)： 184-185, 191. (in Chinese)

[8]李省恒， 杜建安， 孔方桂. 身管等齐膛线缠角检测方法研究[J]. 新技术新工艺， 2010(1)： 51-52. Li Shengheng, Du Jianan, Kong Fanggui. Research of testing method for twist angle of uniform twist rifling[J]. New Technique and New Process， 2010(1)： 51-52. (in Chinese)

[9]吴会民， 牛长根. 弹丸膛内运动分析[J]. 火炮发射与控制学报， 2011(2)： 62-65. Wu Huimin, Niu Changgen. Analysis on moving characteristics of projectile in bore[J]. Journal of Gun Launch & Control， 2011(2)： 62-65. (in Chinese)

[10]曾志银， 马明迪， 宁变芳， 等. 火炮身管阳线损伤机理分析[J]. 兵工学报, 2014, 35(11)： 1736-1742. Zeng Zhiyin， Ma Mingdi， Ning Bianfang, et al. Anlysis of rifling land damage mechanism of gun barrel[J]. Acta Armamentarii, 2014, 35(11)： 1736-1742. (in Chinese)

[11]王宝元， 衡刚， 周发明， 等. 火炮测试技术进展[M]. 北京： 国防工业出版社, 2011.

Study on Barrel Rifling Types and Its Dynamical Effect

WANG Bao-yuan, XU Yao-feng, ZHOU Fa-ming, LIU Jun, HENG Gang

(Northwest Institute of Mechanical and Electrical Engineering, Xianyang 712099, China)

In order to compare dynamic responses of gun barrels with uniform rifling, increasing rifling and combined rifling, the dynamic analysis method was used to analyze the changing rules of the driving edge force, the axial acceleration of the projectile constrained by rifling and muzzle vibration responses for different rifling style. The results show that, near the muzzle, the driving edge force is lowest for the uniform rifling but largest for the increasing rifling. The driving edge force curve for the uniform rifling is smooth, however, for the combined rifling the force changes severely and the curve has large gradient. As soon as the nose of the projectile exits the muzzle, the driving edge force for the combined rifling changes more than three times suddenly and the axial acceleration of the projectile constrained by combined rifling has a jump near the muzzle. Compared with uniform rifling, the muzzle rotation velocity and rotation acceleration around the barrel axis increase about 92.7% and 367.5% respectively for the combined rifling. The uniform rifling is benefit for the projectile moving stably in bore and benefit for weakening the muzzle vibration.

gun； barrel； rifling； driving edge force； muzzle vibration

1673-3193(2017)01-0042-06

2016-03-04

王宝元(1959-)， 男， 研究员级高工， 硕士， 主要从事机械结构动力学和测试技术研究.

TJ301

A

10.3969/j.issn.1673-3193.2017.01.009