基于电感特征的开关磁阻电机电流斩波控制策略
2023-03-31陈越蒋启龙王金锁姚卫丰
陈越,蒋启龙,*,王金锁,姚卫丰
(1.西南交通大学 电气工程学院,成都 611756;2.深圳职业技术学院 机电工程学院,深圳 518055)
开关磁阻电机(switched reluctance motor,SRM)具有结构简单、容错能力强、调速范围宽等优点,自问世以来便得到了快速的发展。但SRM 特殊的双凸极结构和运行时磁路的高度饱和特性,使得其电磁转矩是转子位置角和定子相电流的非线性函数,SRM 的这种特点决定了其具有瞬时输出转矩脉动大的问题。如何降低SRM 的转矩脉动成为电气传动及电机控制领域的研究热点。
目前,国内外学者在SRM 的转矩脉动抑制策略方面做了大量研究。文献[1]针对SRM 电感非线性的特点,通过优化开通角和关断角来提高SRM的运行性能。文献[2]提出一种基于相电感特征的SRM 无位置传感器控制方法,用以提高电机控制中转子位置角度的计算精度。文献[3]提出一种适用于SRM 宽速域调速的离线转矩分配函数(torque sharing function, TSF),该离线TSF 在不增加铜耗的情况下能显著降低转矩脉动。文献[4]在传统转矩分配函数控制策略下,通过对导通角和重叠角进行优化,进一步拓宽了SRM 的调速范围。文献[5]在直接转矩控制下选取一种通用全桥变换器直接与SRM 各相绕组连接,该方法具有良好的动、稳态性能。文献[6]以提高转矩电流比为目标对传统直接转矩控制进行改进,在降低转矩脉动的同时提高了效率。文献[7]在直接转矩的思想上提出直接瞬时转矩控制,该方法以电机瞬时转矩为控制对象,对降低SRM 的转矩脉动有较好的效果。文献[8]采用一种新型四电平功率变换器来改善传统直接瞬时转矩控制电压矢量少的问题,使绕组具有更快的磁化和退磁特性。文献[9]提出一种基于脉冲宽度调制(pulse width modulation, PWM)的SRM 直接瞬时转矩控制方法,该方法在运行时能自适应地调整滞环大小。文献[10]设计了一种比例和积分(proportional integral,PI)参数自适应的电流调节器,能有效改善 SRM 调速系统的运行性能。文献[11-12]提出了基于预测电流控制算法的SRM 转矩脉动抑制策略,以降低电机在换相时的转矩脉动。另外,文献[13-15]中基于模糊控制、神经网络控制及基于迭代学习的控制等智能控制理论也被广泛应用于SRM 的转矩脉动抑制研究。
SRM 在基速下常采用电流斩波控制(current chop control, CCC),但是传统的CCC 难以使实际电流跟踪参考电流,存在相转矩的欠补偿问题。在传统CCC 的基础上,本文提出一种基于电感特征分段控制的CCC 策略(改进CCC)。通过对参考电流进行补偿,增强绕组在换相区间内的转矩输出能力。最后,对所提控制策略进行了仿真和硬件在环实验验证。
1 开关磁阻电机的传统电流斩波控制
1.1 数学模型
在线性模型下,SRM 的第k 相电压平衡方程式可以表示为

式中:ωr= dθ/dt,为转子角速度;e(θ,ik)为第k 相绕组电感变化产生的反电动势。
SRM 转矩的产生遵循磁阻最小原理。在磁路饱和状态下运行的SRM 是一种高度非线性的机电装置,忽略各绕组间互感影响,在磁路线性区域,第k 相所产生的转矩Tk可以近似表示为
SRM 在运行过程中的总瞬时转矩为各相瞬时转矩之和,即合成总瞬时转矩为
式中:Ttotal为总瞬时转矩;m 为电机相数;TL为负载转矩;B 为摩擦系数;J 为转动惯量。
由式(5)可知,线性模式下总电磁转矩是相电流和转子位置的函数,相电流的微小变化将引起相转矩按电流的平方倍变化。考虑实际电机中磁路饱和的影响,相转矩与其电流不完全按照平方的关系变化,但仍随电流的增大而增大。因此,对SRM运行时的相电流进行精确控制是提高运行性能的关键。
1.2 电流斩波控制逻辑
SRM 运行过程中电流波形的形态、电流峰值及其出现的位置都会对电机的运行性能造成影响。传统CCC 下的电流瞬时波形如图1所示,在绕组导通区间,电流滞环控制器对绕组电流进行斩波控制,通过对滞环带的合理设置,可以将绕组电流ik控制在参考电流iref附近波动,得到的电流波形趋近于平顶电流波形。图中:θ0为不对齐位置,θ1为定转子齿开始重叠的位置,θ2为定转子齿全部重合的起始位置,θon和θoff为相绕组开通角和关断角。

图1 斩波控制下瞬时相电流波形Fig.1 Instantaneous current waveform controlled by chopper
CCC 中通常将一个开关管参与斩波的方式称为软斩波,软斩波采用自然续流的方式对绕组进行退磁,电流的变化速率相对缓慢,不易造成转矩频繁的波动,图2 为SRM 的A 相绕组在电动状态下采用CCC 的示意图,us为电源电压;vL为绕组L 的电压;S1 和S2 为开关管;D1 和D2 为续流二极管。参考电流iref由速度环给出,将其与绕组电流ik比较后送入滞环控制器,从而输出开关管的导通逻辑。图2 中设定电流上限ih=iref+0.5h,电流下限il=iref-0.5h,h 为滞环宽度且h=ih-il。当电机某相绕组导通后,下开关管闭合,上开关管参与斩波,绕组电流ik从0 开始上升。当电流瞬时值达到滞环上限值ih时,上开关管关断斩波,电流ik自然续流;当绕组电流ik瞬时值达到滞环带下限值il时,上开关管又重新导通,电流ik开始重新上升。在整个绕组导通区间,上开关管的反复通断使得绕组电流在参考电流附近反复波动。本文功率变换桥选用不对称半桥结构的功率电路。根据其工作过程,定义一相绕组中励磁、续流和退磁3 种开关状态分别为“1”、“0”和“-1”。电流软斩波时,在绕组导通区间内电路工作在“1”和“0”状态。
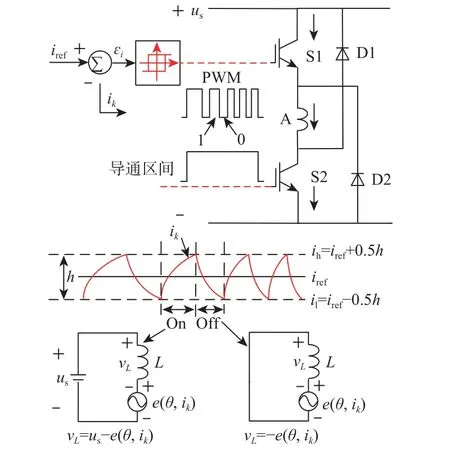
图2 电流软斩波示意图Fig.2 Schematic diagram of soft chopping current control
1.3 转矩变化特征
从式(4)可知,相转矩含有电感Lk关于θ 的偏导,以三相12/8 极SRM 为研究对象,通过有限元仿真得出样机在恒定电流时的电感曲线及其偏导数∂L/∂θ,以I=6 A 为例,如图3 所示。
从图3 可知,在小电感区∂ L/∂θ的值比较小;在电感转折区,∂ L/∂θ急剧增大。一般为了增加励磁相的输出转矩,在小电感区绕组电流就已达到斩波幅值,假设斩波过程电流平均值大小为I0,电机相电感在∂ L/∂θ突变区前期和后期偏导数分别为kL1和kL2,显然kL1≪kL2,在该区域内相转矩有:
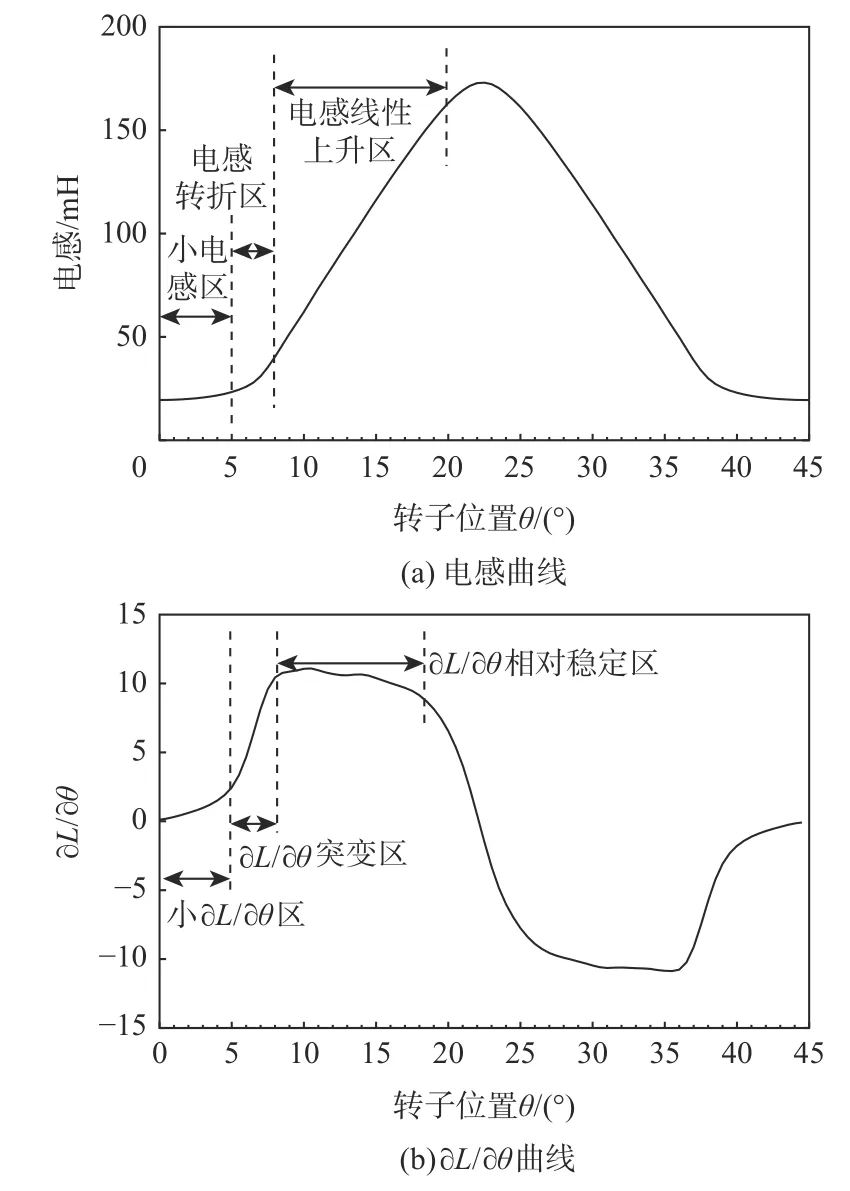
图3 样机I=6 A 时电感曲线及∂ L/∂θ曲线Fig.3 Curves of inductance and ∂ L/∂θ for prototype I=6 A
在小电感区间内,∂ L/∂θ的值比较小,此时电流幅值被斩波带所限,导致在该区间内产生的相转矩很小,此时退磁相产生的转矩通常已进入下降状态,容易造成合成转矩的不足。在电感转折区,∂L/∂θ的值急剧增大,从式(6)可以看出,电机相转矩从一个很小值急剧增大,然而控制器的响应速度往往难以快速跟踪输出,当退磁相转矩的减少量不能抵消励磁相转矩的增加量时,合成转矩又会表现出过补偿现象。之后转子进入电感线性上升区,∂ L/∂θ的值相对稳定,此时CCC 输出转矩也相对稳定。在小电感区及电感转折区,传统CCC 难以保持输出瞬时转矩的稳定,需要采取额外的控制措施。
为了在小电感区使电机的输出转矩能够达到期望值,要求该相绕组在该区间的电流也要达到一定的幅值,这样才能增强电机的转矩输出能力。而传统CCC 的峰值电流被限,在换相的初始阶段,绕组电流难以满足该区间内的转矩输出要求,不仅容易造成大的转矩波动,而且系统在扰动下的动态响应也十分缓慢。为了增强电机的转矩输出能力,提出一种基于电感特征的CCC 策略。
2 基于电感特征的电流斩波控制策略
2.1 斩波电流补偿策略
由第1 节可知,在相绕组导通区间内,小电感区及电感上升区应当有不同的斩波电流。因此,可以根据电感曲线的变化特点进行分段控制。通过有限元仿真所得样机的电感曲线簇及其∂ L/∂θ曲线簇如图4 所示。
由图4(b)可知,电感关于θ 的偏导数∂ L/∂θ在θa和θb附近发生明显变化。因此,以θa和θb为分界点,将绕组导通区间分为参考电流补偿区、过渡区和参考电流非补偿区,并取θa=5°,θb=7.8°。在参考电流补偿区,有θon<θ <θa,此时∂ L/∂θ的值很小,在原参考电流下相绕组的转矩输出能力不足,通过预存的“补偿电流—转速—负载”函数计算出补偿电流Δiref的大小,然后将补偿电流叠加到原参考电流之上,再送入电流滞环控制器进行斩波控制,即实际斩波的参考电流为i'ref=iref+Δiref;过渡区间即为∂L/∂θ 突 变区,有θa<θ <θb,在该阶段内由于∂ L/∂θ快速上升而使得相转矩也快速上升,为了防止合成转矩在该区间内有大的波动,需要将在补偿区间内叠加的补偿电流减小甚至去掉。θc为θa和θb的中点,在θc处提前将补偿电流减小到0;在参考电流非补偿区,即θb<θ <θoff时,∂ L/∂θ的值相对稳定,相转矩在该区间段内也相对稳定,保持原参考电流iref不变,无需进行电流补偿。

图4 样机电感曲线簇与∂ L/∂θ曲线簇Fig.4 Curve clusters of inductance and ∂ L/∂θ of prototype
参考电流补偿值的大小根据转速和负载大小进行调节。轻载时,由绕组电感变化而产生的旋转电动势对绕组电流影响比较大,此时补偿电流的大小主要由电机转速决定;当电机负载较重时,由相绕组电流变化产生的变压器电动势增加,此时补偿电流的大小应主要由负载的大小决定。根据仿真或实验数据拟合出一个“补偿电流—转速—负载”函数,控制器根据该函数实时计算补偿电流值的大小。
开通角θon对换相电流有很大影响,采用在线调节开通角的方式,根据文献[16]计算开通角大小,计算式为
开通角在线调节流程如图5 所示。

图5 开通角在线调节流程Fig.5 Flow chart of online adjustment of turn-on angle
2.2 电流软斩波下的PWM 控制策略
在传统CCC 下,开关管的通断完全由电流滞环控制器决定,控制器根据斩波逻辑输出频率变化的PWM 波,存在开关频率不固定的问题。并且随着转速的升高,电流的变化速率加快,当电流采样速率较低时,存在下一时刻的采样值超出滞环带的情况,控制器无法及时将电流控制在滞环宽度以内,从而也造成了转矩脉动的产生。为了进一步控制相电流,对电流控制器进行改进,输出频率固定的PWM 波来控制开关管的通断。
固定频率斩波控制的实现过程如图6 所示,Ts为原电流软斩波时控制周期;Ts′为固定频率控制时的周期。当电机运行于低速状态且滞环宽度不是太小时,电流的变化速率较慢,电流斩波的频率较低,此时开关管在开通状态“on”或关断状态“off”任意一个状态上的保持时间比较长。在整个“on”阶段,绕组两端承受正压,处于正向励磁状态,此时可将“on”阶段视为一占空比D=1 的PWM 波;在整个“off”阶段绕组都处于零压状态,绕组自然续流,可视为占空比D=0 的PWM 波。此时可以在“on”或者“off”阶段用频率固定、占空比可调的PWM 波来代替原电流软斩波输出的PWM 波形,实现定频控制。
定频控制过程仍然按照电感特征的区间分段进行控制,在电流补偿区,需要使相电流快速达到目标参考值,而实际电流通常需要经过多个周期才能达到目标,因此,此阶段内PWM 的占空比设置为1,即控制器按照参考电流进行补偿后的斩波策略输出控制逻辑。在电流非补偿区,当绕组电流上升至ih或下降至il时达到滞环带的边界点,按电流斩波方式关断或开通开关管,而在滞环宽度内按照固定频率的PWM 进行控制,并在滞环带的边界点处进行PWM 占空比的更新。图6 中ik和 i′k分别为原电流斩波控制和固定频率PWM 控制时的电流波形。在电流的上升阶段,施加占空比略小于1 的PWM 波,经过几个PWM 周期后,绕组电流 i′k到达滞环带的上斩波点并更新PWM 的占空比;在电流下降阶段并不完全关断主开关管,而是施加占空比略大于0 的PWM 波。之后在每个电流斩波周期内施加相同的控制,单个控制周期内电流变化的幅值变小,不易出现超调,从而产生的转矩也更加平滑。

图6 电流控制器PWM 调制图Fig.6 PWM diagram of current controller
所提电流软斩波控制方法的系统框图如图7所示,主要由速度环控制器、参考电流补偿器、电流控制器、功率变换器、位置传感器及开关磁阻电机等组成,图中:ωref为角速度参考值,ωact为角速度实际反馈值,εω为角速度误差值,ω 为角速度,S1~S6 为功率开关。
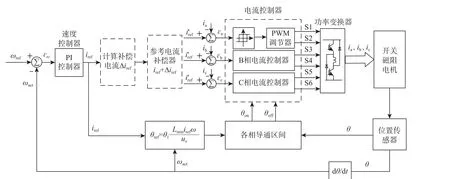
图7 电流软斩波控制系统框图Fig.7 Block diagram of soft chopping current control system
3 仿真与实验
基于第2 节的CCC 方法,搭建了12/8 极三相SRM 控制系统仿真模型进行实验,电机模型根据查表法建立。仿真参数如下:额定电压为540 V,额定功率为7.5 kW,额定转速为1 000 r/min,定子相绕组电阻R=1.1 Ω,电机系统转动惯量J=0.02 kg·m2,摩擦系数B=0.001 Ns/m²,仿真中在线调节开通角,关断角θoff=19°。电流斩波滞环宽度h=1 A,PWM 频率为10 kHz,设定电流上升阶段占空比D=0.9,下降阶段D=0.1。为了验证本文所提策略对于提升电机运行性能的有效性,采用转矩脉动系数指标进行对比,转矩脉动系数 KT可以表示为
式中:Tmax、Tmin和Tav分别为稳态时最大转矩、最小转矩和平均转矩。
通过仿真获得不同转速和负载下的最优参考电流补偿值,仿真结果如图8 所示。

图8 参考电流补偿值曲面Fig.8 Compensation surface of reference current
根据仿真结果拟合出的“Δiref- n-TL”的函数表达式为
图9 为电机负载转矩为30 N·m,转速为300 r/min时传统CCC 与改进CCC 后的电压、电流及瞬时转矩的仿真波形。图10 为两相间的典型换相转矩波形,可以看出,传统CCC 初始导通阶段转矩上升缓慢,然后又急剧上升,合成转矩呈现出从过小到过大的变化;而改进CCC 明显提升了初始导通阶段励磁相绕组的输出转矩,励磁绕组在小电感区有更强的转矩输出能力,相转矩的上升过程更为平稳,没有出现过大的相转矩峰值,有效避免了换相过程中大的转矩波动。

图9 n=300 r/min,TL=30 N·m 仿真结果Fig.9 Simulation results at n=300 r/min and TL=30 N·m
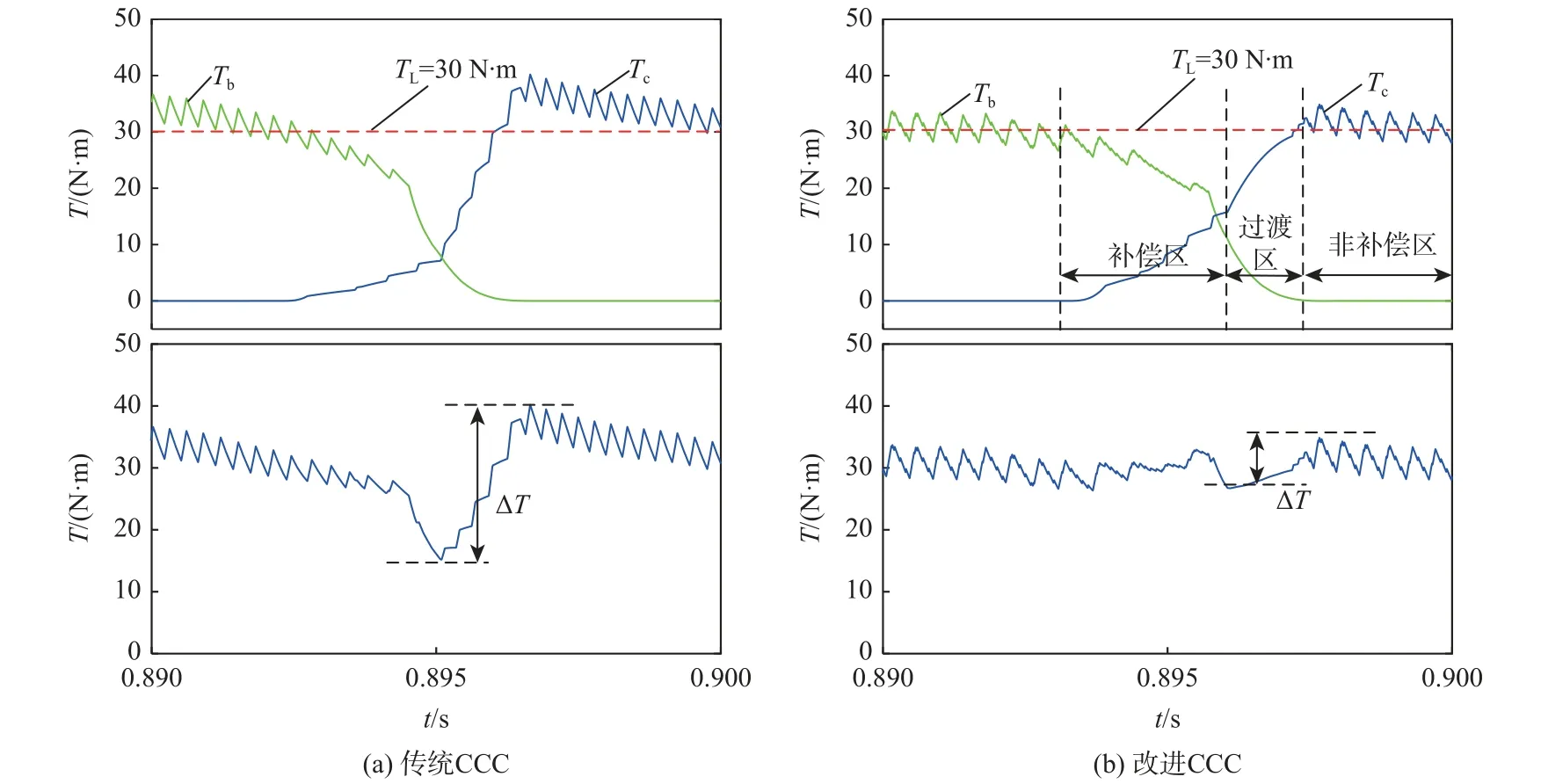
图10 典型换相转矩波形Fig.10 Typical commutation torque waveform
图11 和 图12 负载转矩为30 N·m,转速 为500 r/min 和1 000 r/min 时的仿真波形。可以看出,在励磁相绕组导通后,励磁相的电流得到补偿,能够有效增强换相初期的转矩输出能力,在非补偿区采用固定频率的PWM 波控制,使得输出转矩更为平缓。
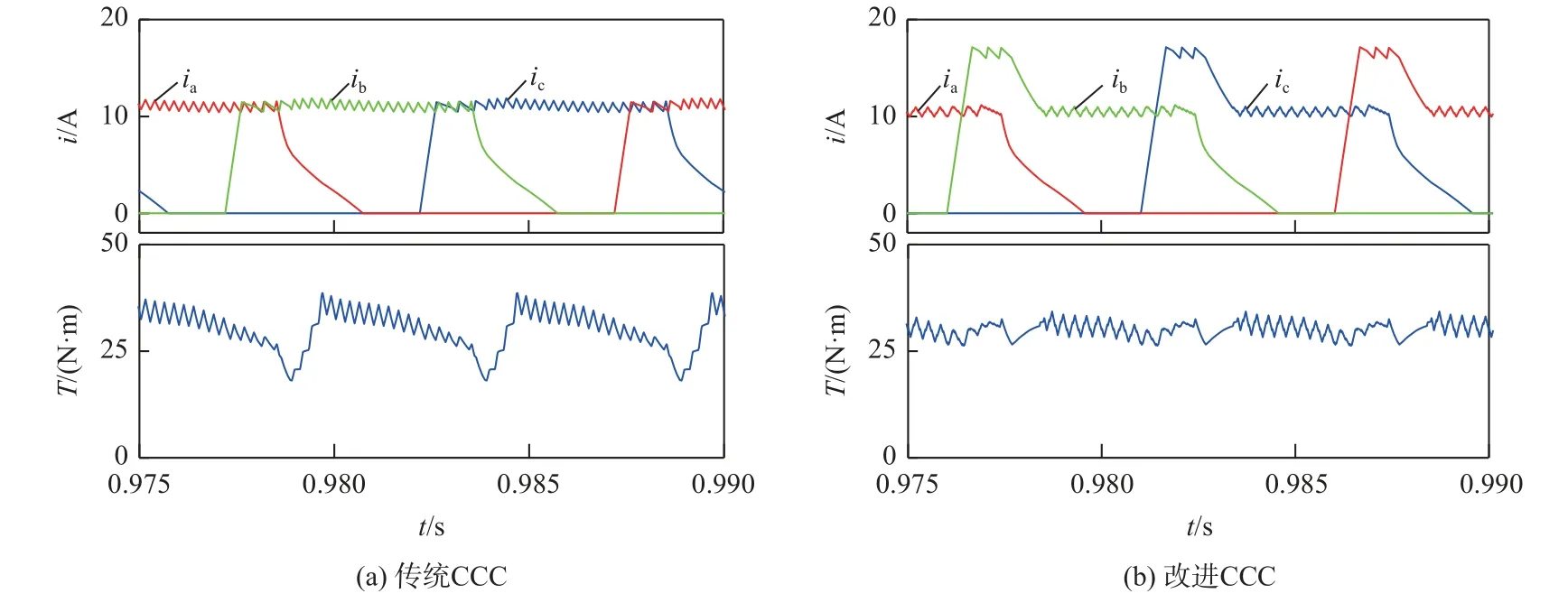
图11 n=500 r/min,TL=30 N·m 仿真结果Fig.11 Simulation results at n=500 r/min and TL=30 N·m
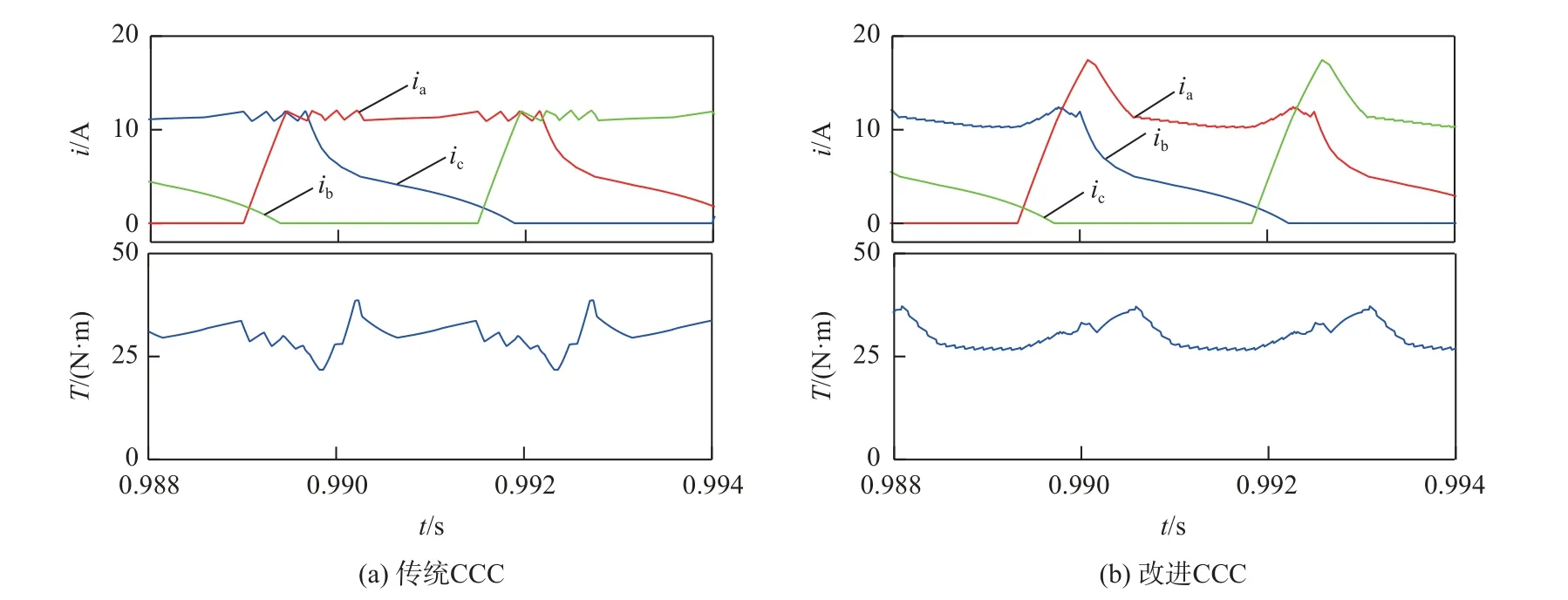
图12 n=1 000 r/min,TL=30 N·m 仿真结果Fig.12 Simulation results at n=1 000 r/min and TL=30 N·m
电机转速分别为300,500,1 000 r/min 时,传统CCC 转矩脉动分别为84.4%、70.1%和56.2%,改进CCC 后的转矩脉动分别为28.8%、26.9%和36.8%。在额定转速下运行时,电机的运动电动势增加,转矩脉动系数的减小幅度变小,但改进CCC 的转矩脉动系数相比于传统CCC 仍然能够得到有效降低,仿真结果表明了所提策略的有效性。
为了进一步验证所提策略的有效性,基于RT BOX 硬件在环实验平台,对所提策略进行实验验证。控制算法通过以DSP 为核心的控制器实现,电机及功率回路通过RT BOX 仿真盒子模拟实现。硬件在环实验参数与仿真一致。图13~图16 为电机转速为300,500 r/min,负载转矩为10,30 N·m 时稳态相电流和瞬时转矩波形。其中,图13~图14中波器的时间刻度为每格10 ms,图15~图16 中波器的时间刻度为每格5 ms。

图13 n=300 r/min,TL=10 N·m 实验结果Fig.13 Experimental results at n=300 r/min and TL=10 N·m

图14 n=300 r/min,TL=30 N·m 实验结果Fig.14 Experimental results at n=300 r/min and TL=30 N·m
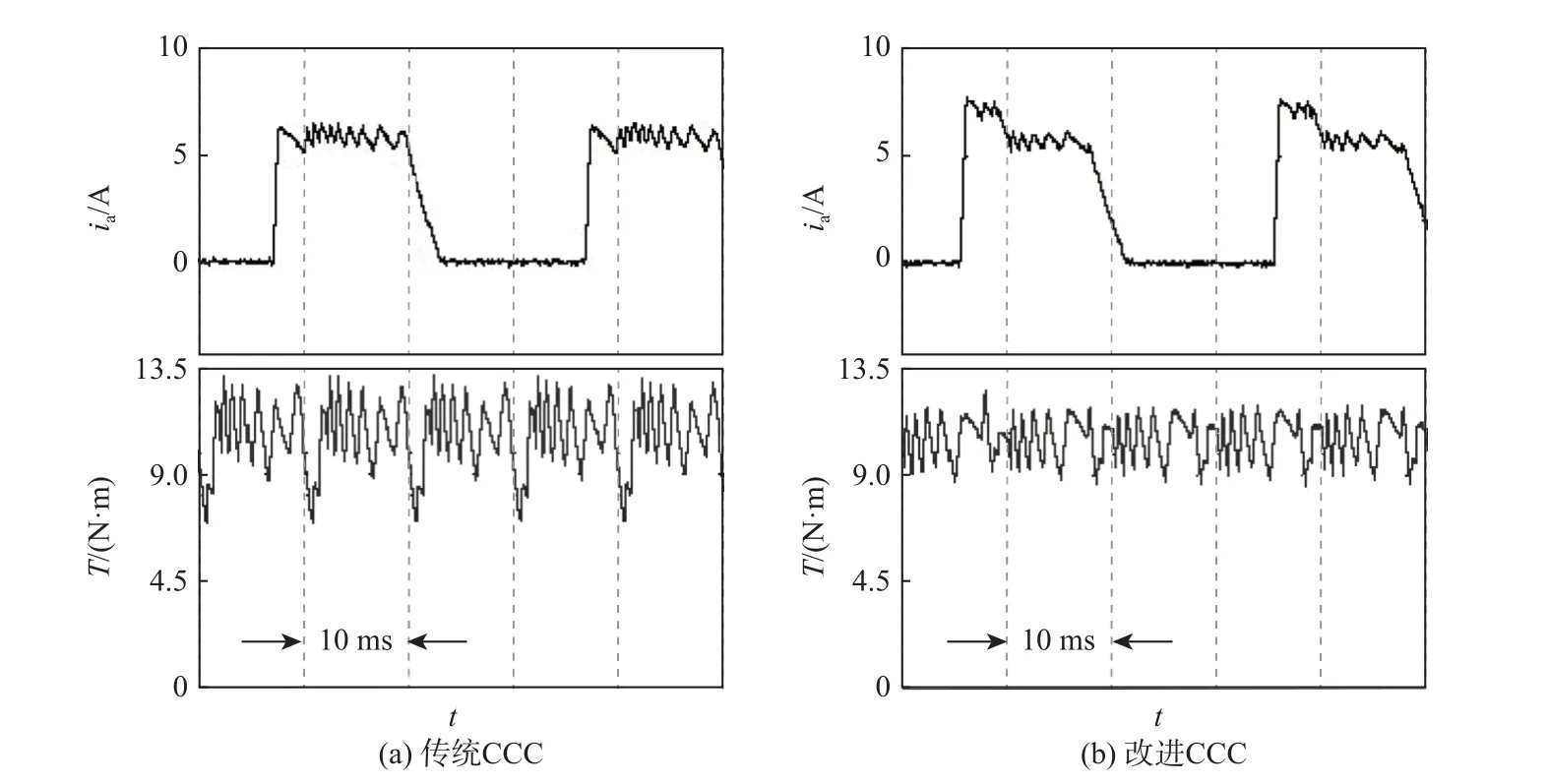
图15 n=500 r/min,TL=10 N·m 实验结果Fig.15 Experimental results at n=500 r/min and TL=10 N·m
从图13~图16 可以看出,在传统CCC 下,由于电流滞环控制的作用使得相电流的幅值被限,造成换相过程中励磁相绕组的转矩输出不足,随着负载的加重,转矩脉动也越大。采用改进CCC 后,换相区间的参考电流得到补偿,绕组电流明显提高,增加了励磁相绕组的转矩输出能力,能够对换相区间的转矩起到补偿作用。在负载转矩为30 N·m时,励磁相绕组的补偿电流值更大,对换相区间内的转矩脉动抑制作用也更明显。

图16 n=500 r/min,TL=30 N·m 实验结果Fig.16 Experimental results at n=500 r/min and TL=30 N·m
图17 和图18 分别为负载转矩为10 N·m 和30 N·m 时2 种方法的转矩脉动系数对比图。可以看出,改进CCC 在不同转速下都能有效减小转矩脉动,并且在负载较重时,转矩脉动抑制效果越明显,验证了所提策略的有效性。

图17 TL=10 N·m 时转矩脉动系数对比Fig.17 Comparison of torque ripple coefficient at TL=10 N·m

图18 TL=30 N·m 时转矩脉动系数对比Fig.18 Comparison of torque ripple coefficient at TL=30 N·m
4 结 论
以三相12/8 极开关磁阻电机为研究对象,对SRM 的CCC 技术进行了研究。通过仿真和硬件在环实验分析,得出以下结论:
1)传统CCC 在电感的线性上升区能获得较好的控制效果,但在低电感区及电感转折区难以保持合成瞬时转矩的稳定。
2)为了增强低电感区间的转矩输出能力,采用了一种基于电感曲线分段,对参考电流进行补偿的控制策略,并在电感曲线的线性上升阶段,采用固定频率的PWM 波进行控制,使得输出转矩更平滑。
3)相比传统CCC,本文改进CCC 能有效减小换相区内间的转矩脉动。
