多种群合作学习的多模态多目标路径规划算法
2023-03-31赵萌路辉王诗琪杨思旖王赞
赵萌,路辉,王诗琪,杨思旖,王赞
(北京航空航天大学 电子信息工程学院,北京 100191)
多模态优化问题旨在找到多个全局或局部最优解,为决策者提供多样的选择,增加决策的鲁棒性;多目标优化问题是指通过权衡多个目标的最优化,为决策者提供更好的选择,提高决策的实用性,与单目标的全局最优点不同,多目标优化的最优解通常用Pareto 解集表示,集合中的解是相互非支配的。多模态多目标优化(multimodal multi-objective optimization, MMO)问题指具有多个全局或局部最优Pareto 解集的优化问题[1],在实际应用中,每个解集包含多种备选方案。丰富的决策方案不仅可以保障决策的有效性,还可以减少突发事件导致的经济损失。
在路径规划问题中,决策者希望可以同时获得满足目标需求的多条路径,从而保障决策的稳定性。目前大多数研究针对最小化路径长度的规划需求,在满足约束条件的前提下同时规划出多条最短路径[2-3],这是一种单目标多模态的优化问题。然而,单一目标通常难以满足人们的实际需求,考虑到路网环境的不确定性,人们希望可以同时获得多条路径长度、堵塞路段数量、交叉路口数量等目标值最优且相等的路径。因此,在路径规划问题中,多模态优化与多目标优化具有紧耦合的关系。虽然已经有学者对多目标路径规划问题进行了深入研究[4-7],但是由于问题建模复杂,求解难度大,关于多模态多目标路径规划问题(multimodal multiobjective optimization path planning, MMOPP)的研究成果却寥寥无几。尽管多式联运问题的研究正处于白热化阶段,但是这些研究往往只考虑运输成本和时间成本[8-9],缺少在多模态优化需求条件下,针对复杂路网中超多目标优化问题的研究。
从应用需求的角度分析,MMOPP 问题的研究通常分为2 种。一种是针对复杂任务中的路径规划[10-12],决策者需要同时考虑路径长度短、有途经点等规划需求。另外一种是考虑物流配送需求的车辆路径规划[13-14],这种问题的研究通常不需要考虑路径的多样性,主要考虑配送车辆的装载量约束与配送网点的时间约束。本文针对复杂路网中MMOPP 问题的研究需求,在多模态优化需求条件下,研究超多目标路径规划问题。相关研究成果可以为车辆或无人载体在复杂路网中的路径规划提供理论与技术支撑。
经典的路径规划算法,如A*算法、Dijkstra 算法等仅考虑路径长度的优化,难以实现对MMOPP 问题的求解。因此,大多数学者引入具有自组织、自适应、自学习特性的群体智能算法实现多目标路径规划。文献[15]将蚁群算法与Dijkstra 算法相结合,通过丰富路径搜索方向,解决了路径长度短、路径平滑度高、机器人行进安全性高3 种路径规划需求。文献[16]提出用强化学习算法优化蚁群算法的参数,提高了算法的全局搜索能力。除蚁群算法外,粒子群优化(particle swarm optimization, PSO)算法[17]、灰狼优化算法[18]、萤火虫算法[19]、天牛群算法[20]等也可用于解决多目标路径规划问题。针对无人机三维作业场景的特殊性,文献[21]通过在NSGA-II算法中引入增加、删除算子,同时解决了路径长度短与躲避威胁区域2 种路径规划需求。此外,无人机燃料损耗的最小化也通常是路径规划问题中需要考虑的优化目标之一[22]。
大多数算法只考虑到了路径规划中的多目标需求,尽管这类算法的搜索能力强,收敛性好,但是由于算法设计过程中没有考虑多模态的规划需求,决策空间内解的多样性难以得到保持,决策的鲁棒性受限。因此,为提升算法的搜索能力与寻优能力,提高解的多样性,本文在MMOPP 问题的研究中侧重解决路径规划问题中的多模态需求,在PSO 算法框架下,提出多种群合作学习(multi-swarm cooperative learning, MSCL)算法。利用多个种群的合作搜索,将多目标优化问题转化为多个单目标问题进行求解,丰富决策空间内解的多样性,同时,兼顾算法在目标空间不同维度上的搜索能力。此外,为了缓解编解码匹配的不唯一性引起的搜索效率低的问题,提出利用解码经验表传递有效的解码经验,以提高算法的寻优能力。算法验证阶段使用的MMOPP 测试集包括对路径长度、道路宽度、道路拥挤度、堵塞路段等待优化目标的数值量化,并且包括必经点问题的求解约束。因此,本文的仿真测试实验与实际应用场景具有紧耦合的关系。仿真测试结果验证了多种群合作学习算法可以并行解决多模态和多目标的路径规划需求,与其他算法的比较结果说明了本文所提算法具有更强的搜索能力与寻优能力,并且解的多样性更好。
1 多种群合作学习算法
多种群合作学习算法是利用多个种群的无交叉搜索并行解决多模态和多目标的路径规划需求。如图1 所示,其中 f1,f2,···,fn为不同的优化目标。算法实现的过程分为3 个阶段:首先,依据地图中关键路径点的数量对路径码进行编码;然后,将初始化后的种群划分为多个子种群,明确每个子种群的优化目标;最后,依据子种群的优化目标对个体的路径码进行解码,计算相应的适应度值,并保留精英解对应的路径。整个过程持续循环,直到满足最大迭代次数。
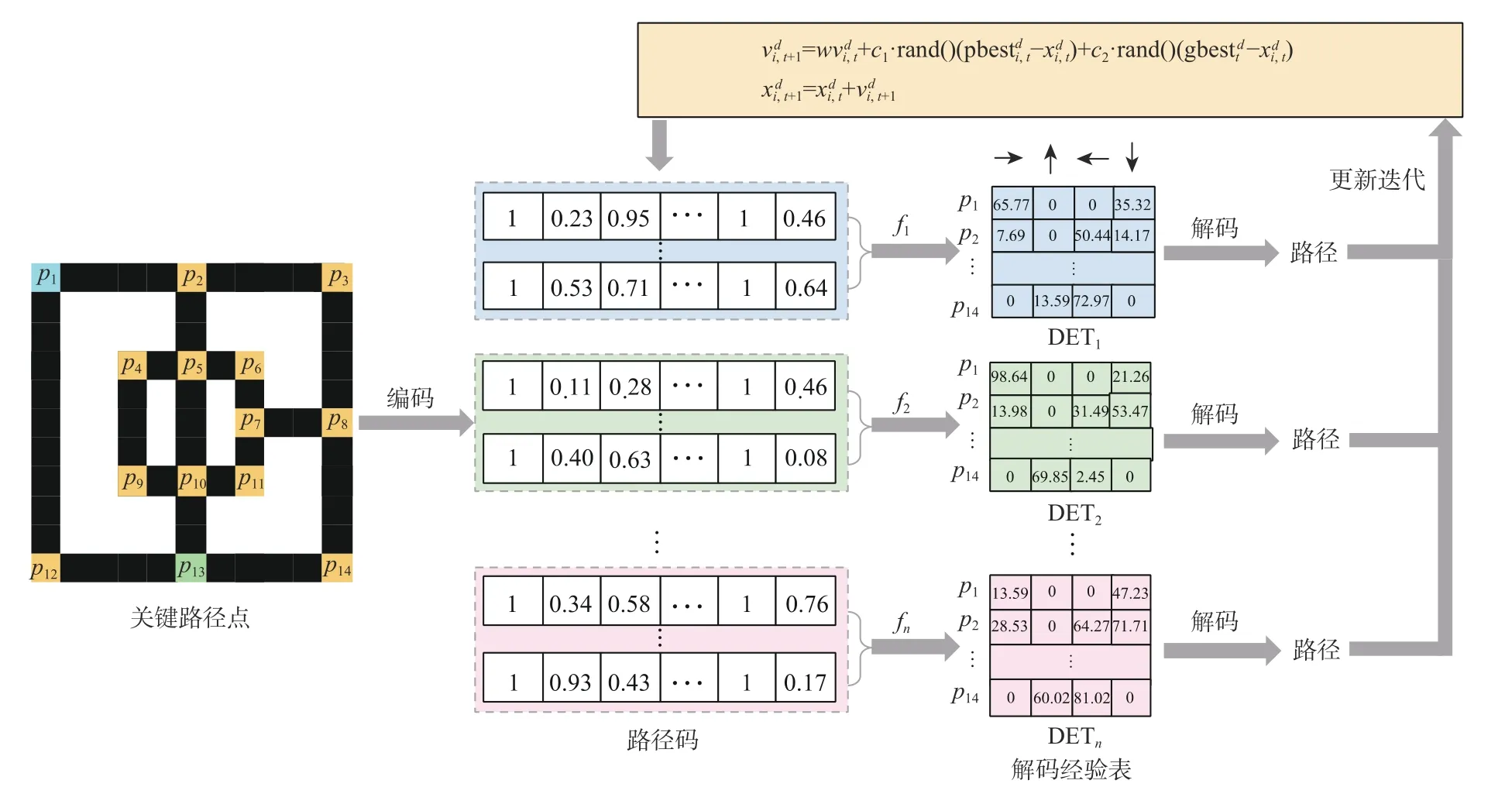
图1 多种群合作学习算法框架Fig.1 Framework of the proposed algorithm
1.1 基于关键点的路径编码
为了降低可行解的搜索难度,利用地图中的关键路径点表征路径信息。如图2 所示,用1、2、3、4 分别表示路径节点与其右、上、左、下的节点具有邻接关系。假设任意路径节点 rj处的可行进方向集合 Wj,如果 rj属于关键路径点集合P={p1,p2,···,pK},则一定满足以下条件之一:

图2 关键路径点的提取Fig.2 Extraction of key path points
条件1 card(Wj)>2;
条件2 如果c ard(Wj)=2,则Wj≠{1,3}且 Wj≠{2,4};
条件3 rj∈{S,T}。
其中 j=1,2,···,R,R为地图所有路径节点的数量,K为关键路径点的数量,且 K <R。S和 T分别为路径的起点和终点。
显然,关键路径点的提取不会影响可行路径的搜索,而且可以通过减小解空间的维度提高可行解的搜索效率。因此,采用地图中关键路径点数量K定义粒子编码的维度,即粒子个体是 K维的实数码,记为路径码。
1.2 基于多目标分解的子种群划分
在多种群合作学习算法中,种群的初始化采用随机数生成器的方式,即vdi,1=rand(0,1),xdi,1=rand(0,1),其中,d=1,2,···,K。然而,如图3 所示,当有3 个优化目标(最小化)时,由于目标空间内的最优解在同一区域,所以,种群中所有粒子的搜索方向是一致的,从任意目标空间的切面看,受全局最优解的牵引,粒子均朝向左下角(最小值)移动。然而,多模态路径规划的目标不是找到一个全局最优解,而是需要综合多个目标,搜索到多个最优解。当优化目标较多时,种群中的粒子具有朝向同一目标区域的搜索趋势,容易出现早熟现象,即单一种群有限的搜索能力会影响解的多样性。因此,为了提高算法的搜索能力与寻优能力,本文提出基于多目标分解的子种群划分策略。

图3 有3 个优化目标时单一种群的粒子群寻优过程Fig.3 Optimization process of particles when there are three objectives to be optimized
根据Pareto 解集的定义,某个解在单一目标维度上最优,即有机会成为Pareto 最优解。因此,在多种群合作学习算法中,种群会依据优化目标的个数进行均匀划分,每个子种群在迭代寻优的过程中只负责优化一个目标,如图4 所示,所有粒子具有相同的优化目标,其在目标空间内的运动具有一致性。当有3 个优化目标(最小化)时,每个种群分别负责在目标1、目标2、目标3 的维度内搜索最优解,从而避免由于粒子在目标空间内的一致性移动导致陷入局优的问题。多种群分工协作的机制使得粒子可以在目标空间内分散地搜索,趋向不同的方向寻找最优解,进而实现多目标的分维寻优,提高解的多样性。因此,在多模态多目标路径规划问题的求解中具有更强的搜索能力与寻优能力。
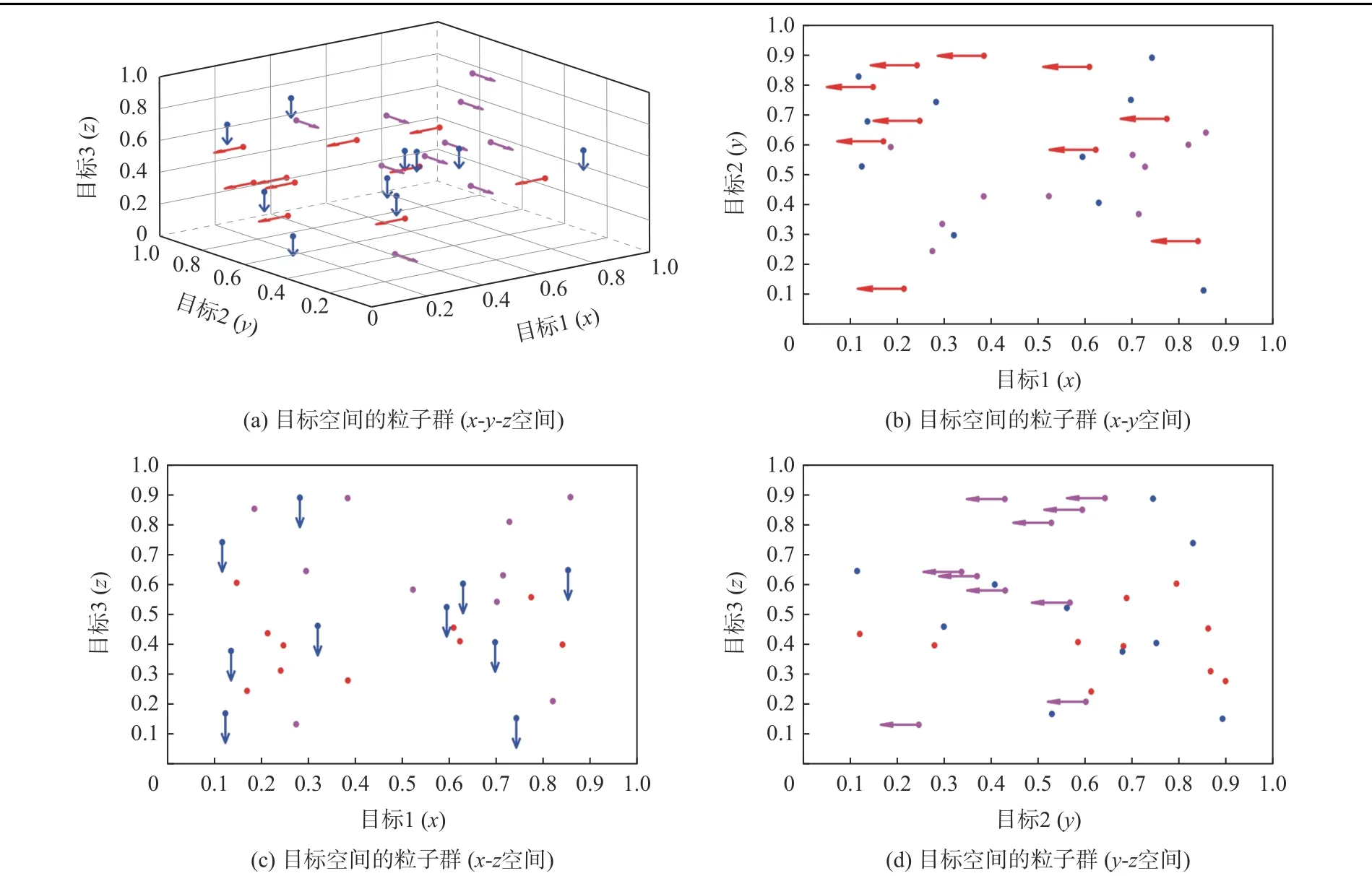
图4 有3 个优化目标时基于子种群划分策略的粒子群寻优过程Fig.4 Optimization process of particles when there are three objectives to be optimized
1.3 基于粒子群的迭代过程
在多种群合作学习算法中,种群中的每个个体根据标准粒子群优化算法更新迭代自身的速度与位置[23]。粒子群优化算法是Eberhart 和Kennedy[24]于1995 年提出的一种基于群体协作的随机搜索算法。该算法的基本思想是模拟鸟群的觅食行为,通过粒子群在解空间内的搜索实现对优化问题的求解。如式(1)和式(2)所示,种群中粒子的状态用速度和位置2 个向量描述:

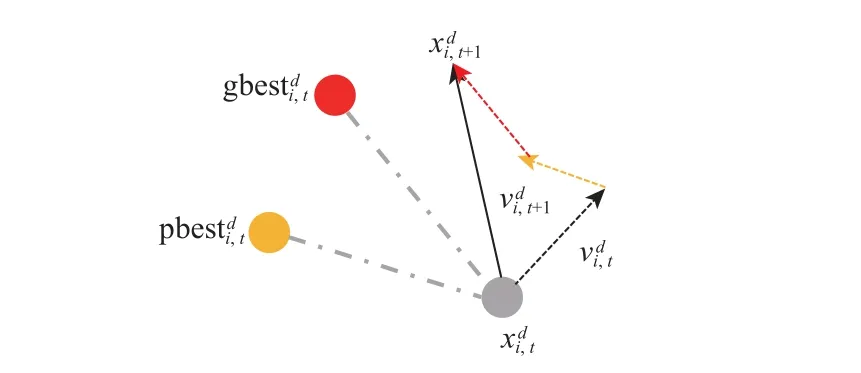
图5 粒子的寻优过程Fig.5 The optimization process of the particles.

1.4 基于解码经验表的路径解码
根据路径规划的需求,从路径起点对应的维度开始解码,然后依据每个关键路径点处的可行进方向依次选择下一个路径点,直至当前的解码维度对应于终点,或重复到达某一路径节点,则停止对该粒子个体(路径码)的解码。如果可连续解码至终点,则得到一条可行路径,计算路径对应的各个目标值,经过非支配排序得到精英解。然而,地图中每个关键路径点都有多个可行进方向,路径码的解码空间不能一一映射地回溯至编码空间。针对这种编解码匹配的不唯一性,提出采用解码经验表传递有效的解码经验,降低解码的不确定性。如图6所示,解码经验表 D是 T×M 的二维矩阵,其中,T为路径码的维度,M为关键路径点的最大可行进方向数量,即 M=max(card(Wv)),其中 v=1,2,···,T。在本文使用的测试问题(test problem, TP)中,M=4。解码经验表中的初始数值为0,在粒子解码过程中,表中数值的更新依据式(5)所示的Bellman 方程:

图6 解码经验表Fig.6 Decoding experience table

3)f =min(q)
式中:q 为从起点到终点的路径点总数;Q(pt+1)为经过 pt+1的所有可行路径中最小路径点总数,如果所有路径都没有通过 pt+1,则 Q(pt+1)=0 ;δ为调节奖励值大小的常数。
此外,为了保障算法的寻优能力,路径码的解码过程不仅参考解码经验表中的经验值,也会依概率 ε随机选择下一个关键路径点。
1.5 算法流程
多种群合作学习算法流程如图7 所示。
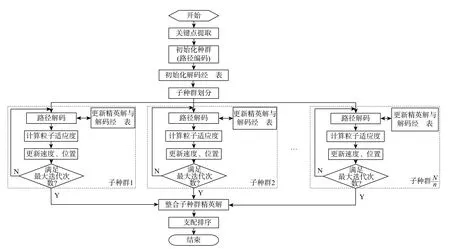
图7 一个多模态多目标路径规划问题的应用实例Fig.7 An application example of MMOPP problem
2 多种群合作学习算法应用实例
为了进一步说明多种群合作学习算法的作用机理,以图8 所示面积大小为11×11 的栅格地图为例,展示粒子在多模态多目标路径规划问题中的编码与解码过程。其中,路径规划的起点与终点分别为 p1和 p13,图8 中红色区域模拟路网中的拥挤堵塞路段,则优化问题可描述为
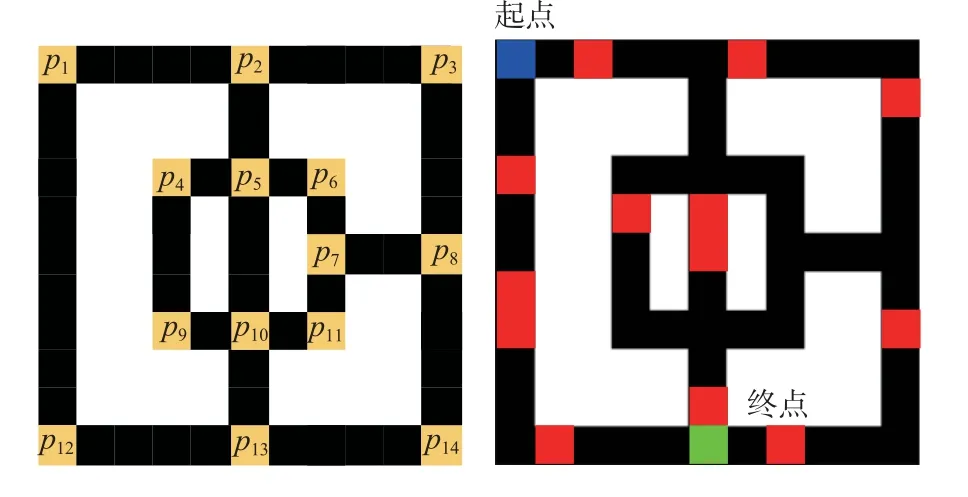
图8 多种群合作学习算法流程Fig.8 Flowchart of multi-swarm cooperative learning algorithm
式中:x 为可行路径;f1(x)、f2(x) 和 f3(x)分别为路径的长度、经过的红色区域数量和经过的交叉点数量。
2.1 路径编码
根据地图中关键点数量提供的决策变量维度,粒子个体将在种群初始化阶段完成编码,如图9 所示,种群中每个粒子个体都是一个14 维的实数码。考虑到路径规划时有3 个待优化目标,因此,种群被划分为3 个子种群,每个种群分别负责搜索最短路径长度、最少红色区域数量、最少交叉点数量对应的路径。
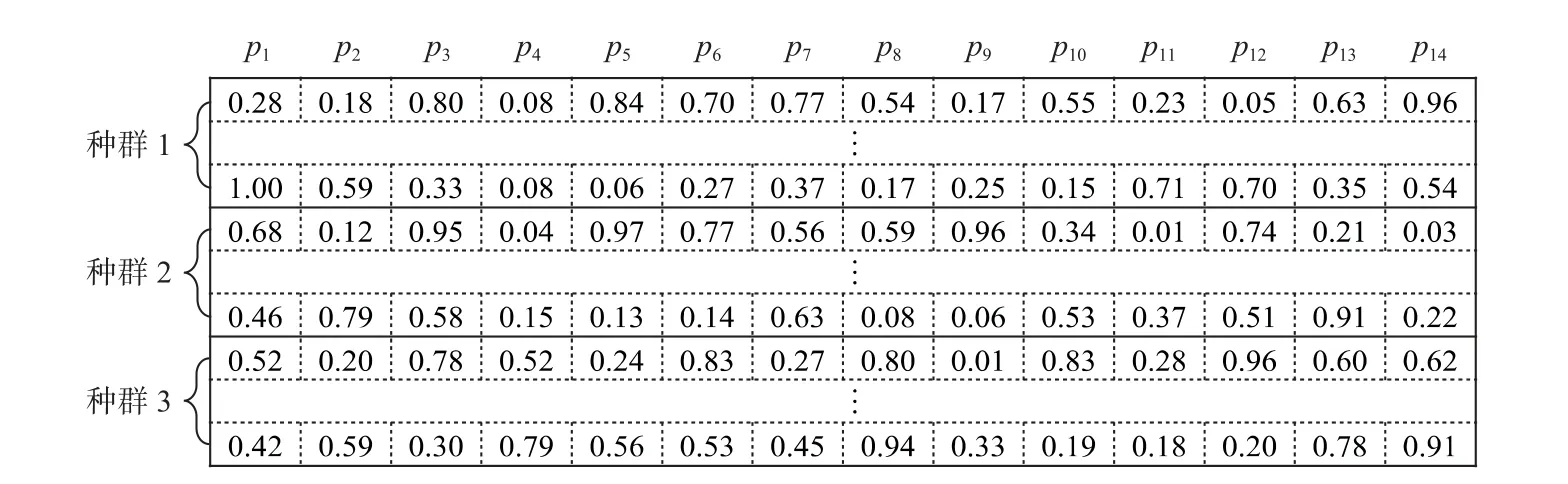
图9 种群(路径码)初始化结果Fig.9 Result of initialing particle swarm (path codes)
2.2 路径解码
在路径解码时,从起点开始基于解码经验表中的经验信息进行解码,图10 为以种群1 为例的解码过程。种群中每个个体的路径码解码都是从起点 p1开 始,依概率 ε (0 <ε <1)选择下一个路径点,即有 ε的概率在邻接点中随机选择下一个路径点,有(1-ε)的概率依据解码经验选择下一个路径点,如果解码经验表中邻接关键点的经验值相同,则随机选择一个作为下一个路径点,如果经验值不同,则选择经验值最大的一个作为下一个路径点。依照此策略持续解码并更新解码经验表,直至下一个路径点是终点,存储可行路径。当个体解码完成时,更新个体的 pbesti,t;当种群中所有个体解码完成时,更新种群的 gbestt。由于种群1 的优化目标是最小化路径长度,因此,pbesti,t与 gbestt的更新仅依据目标值 f1(x)。最后,基于粒子群算法的速度更新公式更新个体位置。整个过程循环迭代直至最大迭代次数。
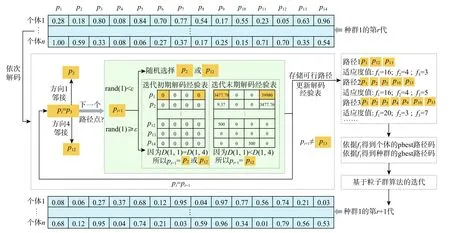
图10 以种群1 为例的路径解码过程Fig.10 Path decoding process of the first sub-swarm that is responsible for optimizing path length
3 仿真测试与验证分析
为了验证多种群合作学习算法在MMOPP 问题上的有效性,本文采用Liang 等[25]构建的MMOPP测试问题集检测算法的性能。此测试集将实际路网地图中的道路特征建模成规则的栅格地图,利用黑色栅格表示可行路段,根据优化目标种类的不同分为三类,共计12 个测试问题。如图11 所示,第1 类测试问题模拟实际路网地图中的拥挤路段,红色栅格表示拥堵路段,其优化目标为最小化路径长度、拥挤路段数量、交叉点数量,根据问题规模的不同,这类问题包含5 个测试问题。在第2 类测试问题中,如图12 所示,其有多个表征不同类型道路信息的F 值(F1,F2,···),用不同的F 值模拟道路拥挤度或道路宽度等信息,优化目标为最小化路径长度和各个F 值,根据优化目标数量的不同,这类问题包含5 个测试问题。图13 为第3 类测试问题模拟了有必经点约束的路径规划需求,而且允许折返路径存在,黄色栅格表示路径规划过程中的必经路段,与第2 类问题类似,每个栅格都有多种不同的F 值(F1,F2,···),其优化目标为最小化路径长度和各个F 值,根据问题规模的不同,这类问题包含2 个测试问题。因此,本文基于本节12 个MMOPP测试问题,从求解时间、搜索能力、寻优能力三方面对算法的性能进行评估,并将实验结果与PSO 算法、融合子种群划分策略的粒子群算法(PSOK)、融合解码经验表的粒子群算法(PSOD)进行对比,进一步分析验证子种群划分、解码经验表策略的有效性。
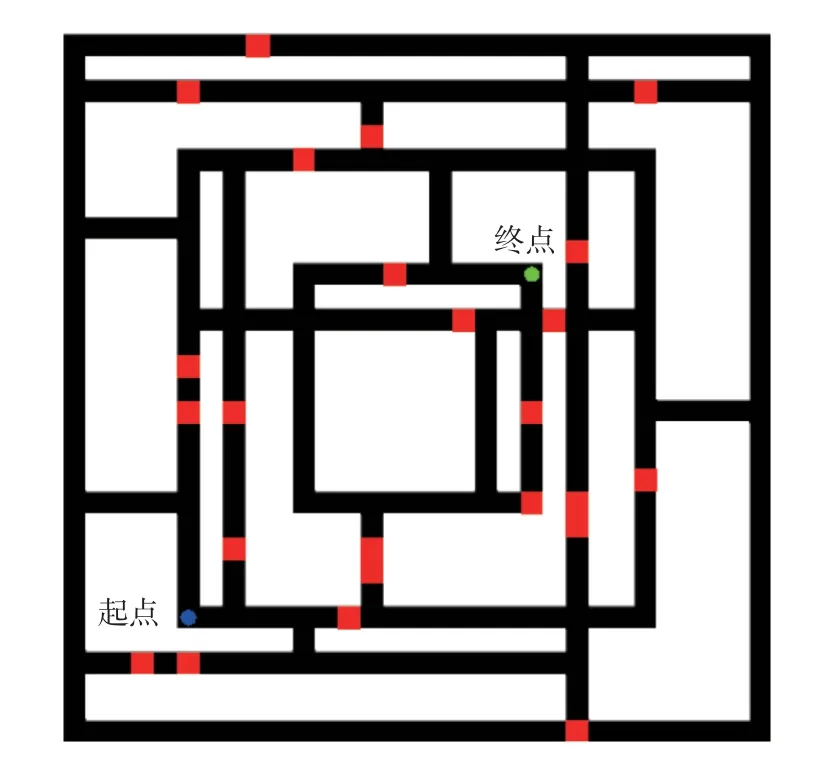
图11 第1 类MMOPP 测试问题实例Fig.11 An example of the first kind of MMOPP test problem
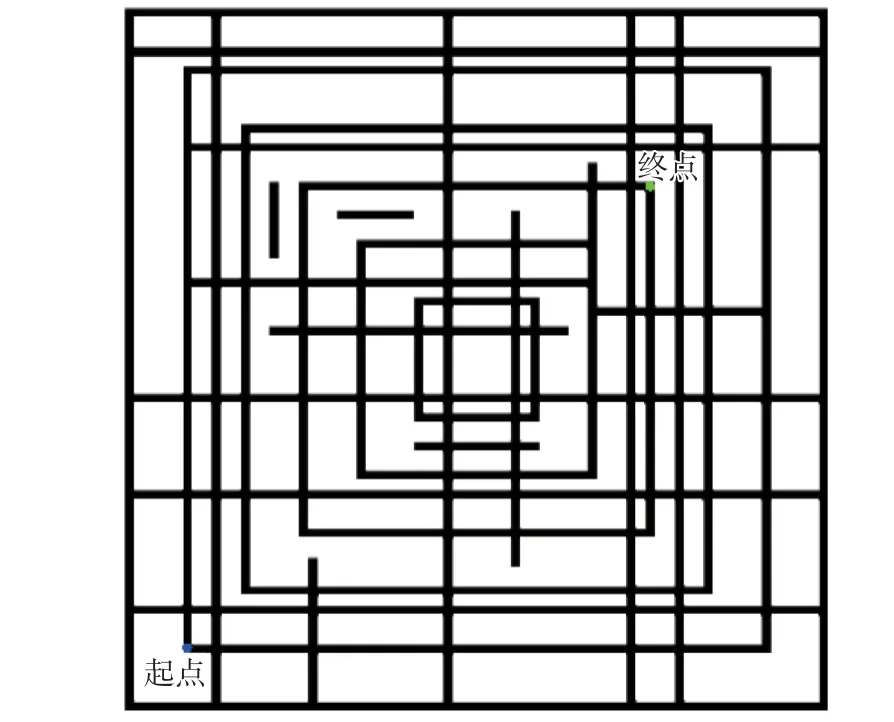
图12 第2 类MMOPP 测试问题实例Fig.12 An example of the second kind of MMOPP test problem
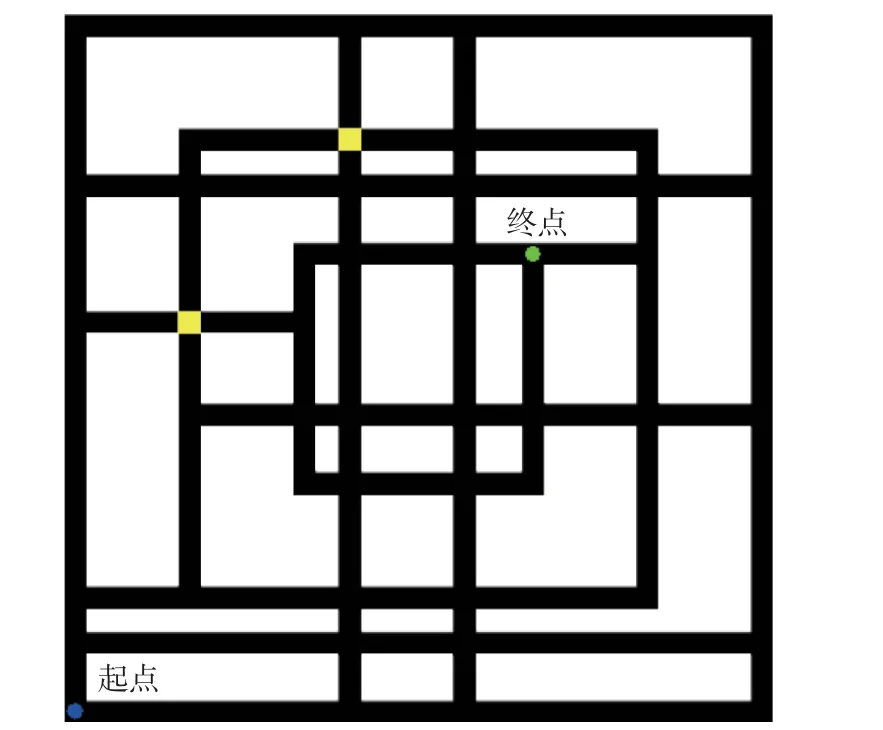
图13 第3 类MMOPP 测试问题实例Fig.13 An example of the third kind of MMOPP test problem
本文的所有实验结果都是50 次实验的平均值,针对同一个测试问题,不同算法的参数、种群大小、迭代次数完全相同。然而,考虑到迭代次数与问题规模大小相关,在本文的仿真测试实验中,针对不同测试问题搜索最优路径所需要的迭代次数是不同的,迭代次数的设置依据问题的规模大小与算法的稳定性表现。具体实验参数设置如表1 所示。
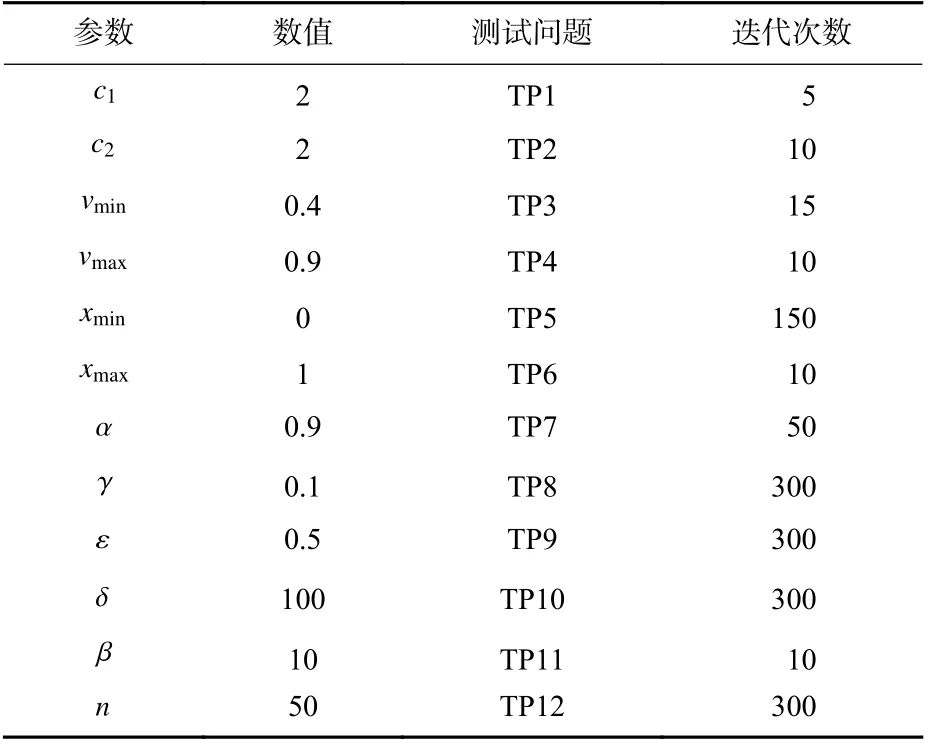
表1 实验参数Table 1 Experimental parameters
表2 为从不同算法搜索时间的对比结果,可以看出,由于在MSCL 算法中,每个种群内部自主选择个体最优解与群体最优解,并且在粒子个体解码过程中有效经验的总结与利用需要耗费额外的时间,因此,算法的求解时间比其他算法长。尽管MSCL 算法的搜索时间较长,但是,不同算法的搜索时间依旧在同一量级。此外,为了分析比较算法的搜索能力与寻优能力,在表3 和表4 中分别记录了不同算法完成最大迭代次数时搜索到满足优化需求的路径总数和最优路径数量。这2 个指标可以反映算法的搜索能力与寻优能力。其中,最优路径是50 次实验的所有结果经过非支配排序后得到的。在每个测试问题中,性能最好的算法结果加粗表示。从表3 和表4 所示结果可以看出,当实验条件完全相同时,在测试问题11 中,PSOD 算法和MSCL 算法性能相同。除测试问题6(TP6)外,本文提出的MSCL 算法可以搜索到更多满足多目标规划需求的路径,并且最优路径的数量明显多于其他算法的规划结果。这是由于MSCL 算法采用了子种群划分策略,平衡了粒子在各个目标维度上的搜索能力,并且经验解码表使粒子在搜索过程中可以有效地利用精英解提供的解码经验。因此,多个种群的合作学习具有更强的寻优能力。此外,本文对比最优路径在搜索到的总路径中所占的比例,并在表5 中展示了实验结果。从最优路径占比的结果可以看出除测试问题6(TP6)外,MSCL 算法的路径规划结果中最优路径占比最多。
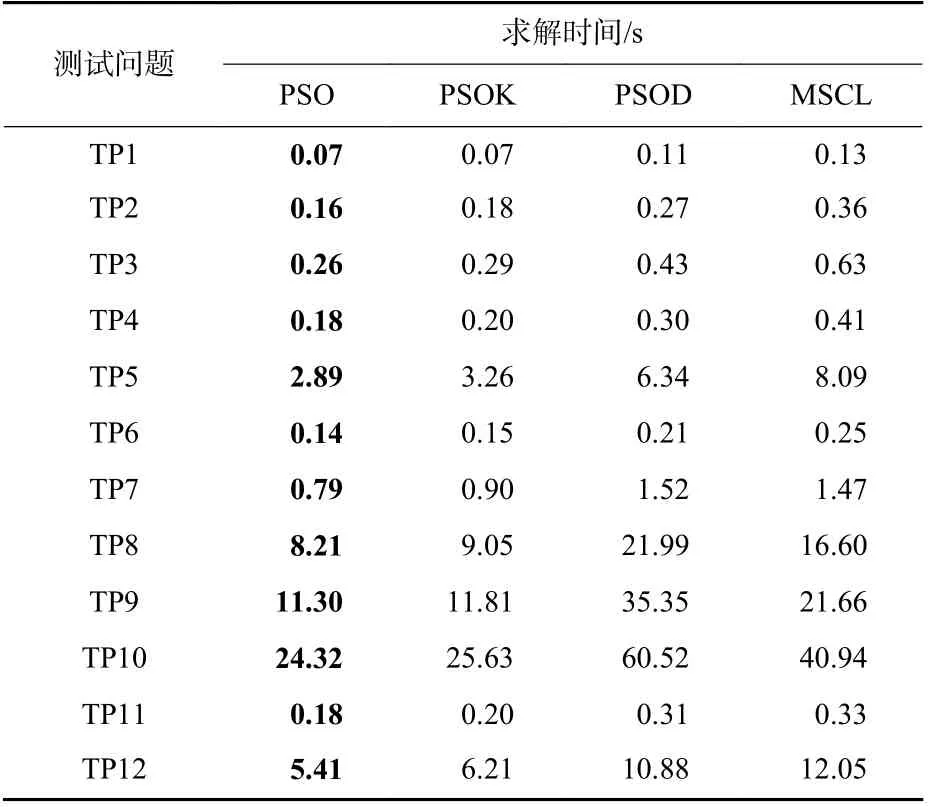
表2 不同算法的求解时间Table 2 Solving time of different algorithms
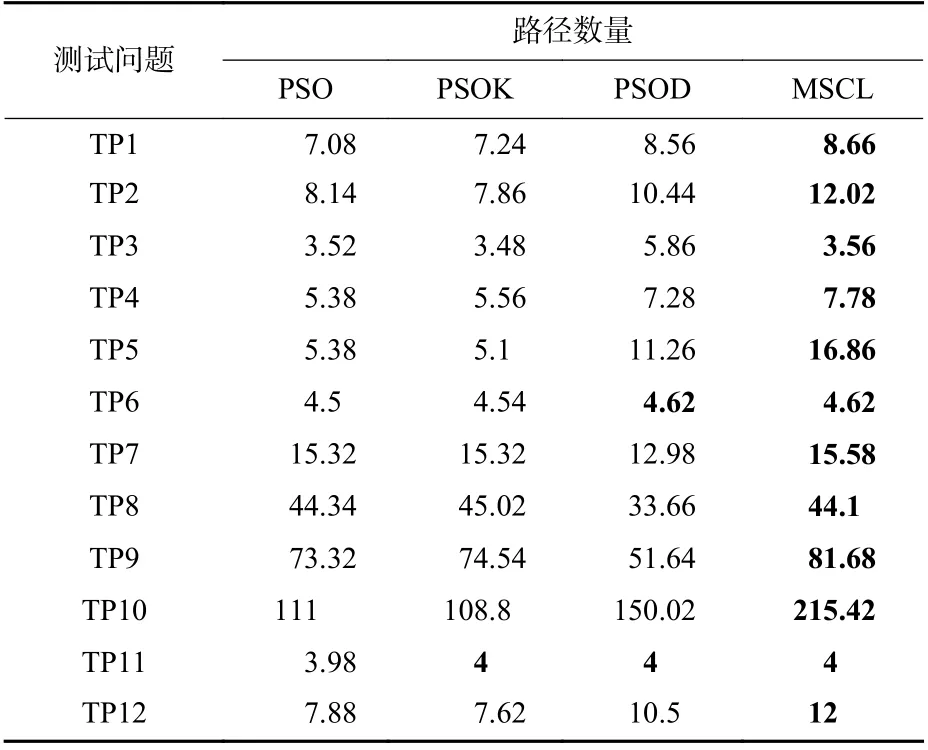
表3 不同算法搜索到的路径数量Table 3 Number of paths searched by different algorithms
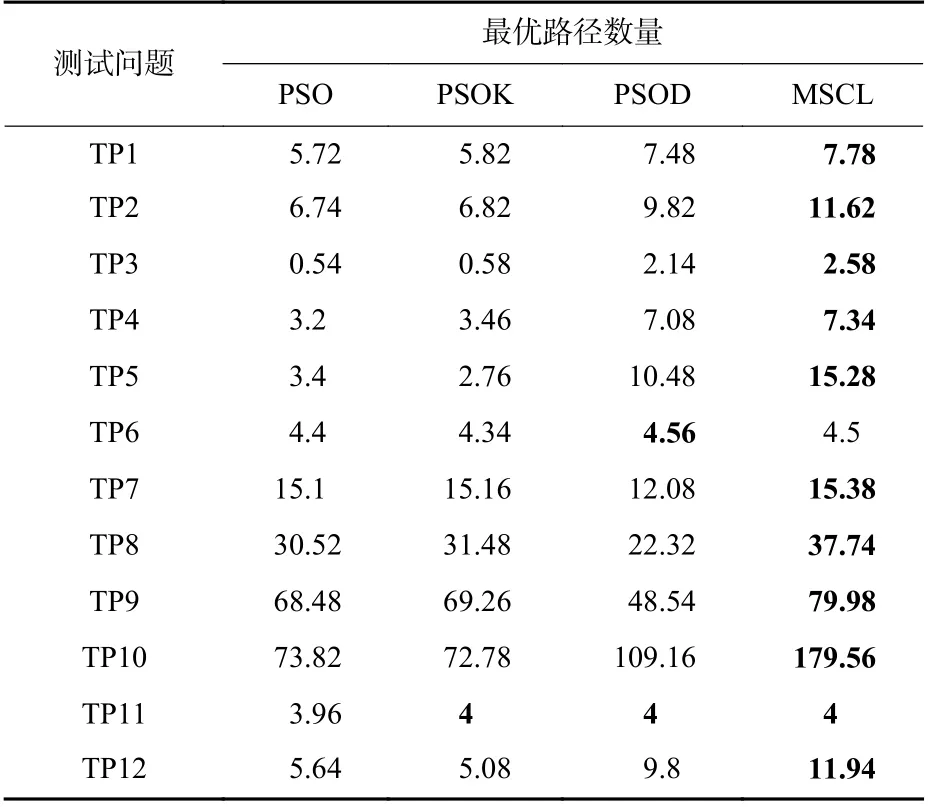
表4 不同算法的搜索到的最优路径数量对比Table 4 Number of optimal paths searched by different algorithms
测试问题11(TP11)只有2 个优化目标,并且在40×40 栅格大小的决策空间内最优路径数量很少。因此,问题规模小,求解难度小,不同算法的性能差别较小。然而,对于测试问题6(TP6),PSOD 算法与MSCL 算法搜索到的路径数量相等,但是PSOD搜索到的路径中最优路径更多,其最优路径所占的比例比MSCL 算法多1.2%。为了分析此现象产生的原因,对不同测试问题的求解难度从优化目标数量、地图变长、编码维度、最优路径数量4 个维度进行分析,通过非支配排序的方式,得到如表6 所示的问题难度等级,等级越低,问题求解越容易。由于测试问题11 和问题12 具有必经点约束,且规划要求不同,为保证分析结果的公平性,未分析这2 个问题的求解难度。
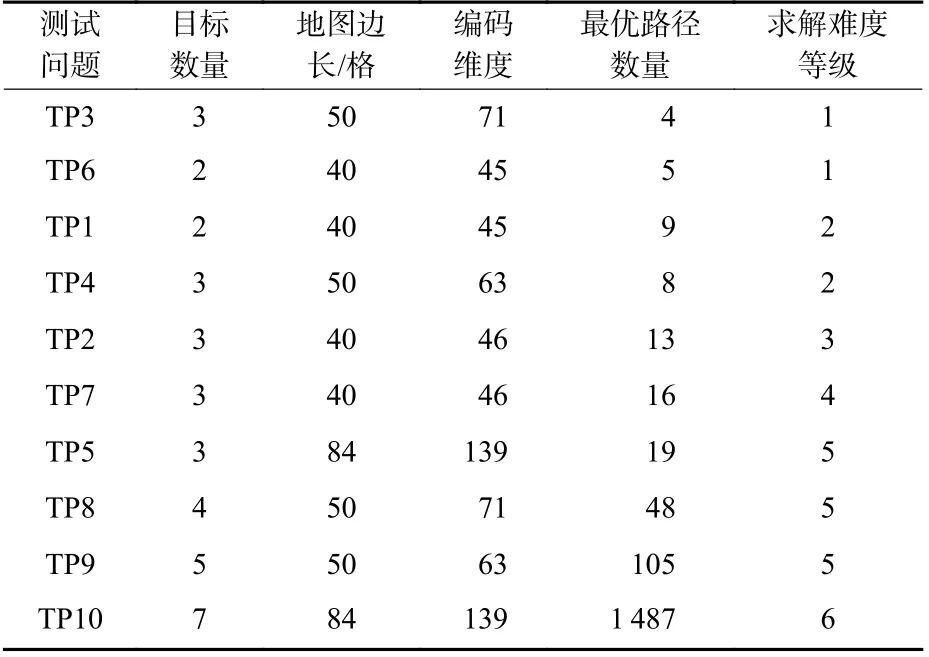
表6 测试问题难度等级分析Table 6 Analysis of difficulty level of test problems
显然,测试问题3(TP3)与测试问题6(TP6)的求解难度低,算法的性能对比结果不明显,由于实验结果是50 次实验的平均值,少数实验规划路径数量少1 条会导致路径数量的指标相差10-2的数量级,最终导致最优路径占比结果的细微差距。因此,为了进一步验证子种群划分与解码经验表的引入提升了MSCL 算法的寻优能力,基于问题难度等级的增加,不同算法在最优路径数量与搜索时间指标上的对比结果如图14 和图15 所示,横轴为测试问题,其难度等级依次递增。
从图14 和图15 可以看出,对于简单的MMOPP问题,不同算法的寻优能力区别不大。但是,相比较于PSO 算法,子种群划分与解码经验表的引入可以有效地提升算法性能。更重要的是,随着问题求解难度等级的依次递增,MSCL 算法与其他算法在寻优能力方面的差距逐渐增大。并且,对于测试问题8~10 这类优化目标多、地图尺寸大的复杂MMOPP问题,MSCL 算法的求解效率、搜索能力、寻优能力都极大地优于其他算法。这进一步说明了多种群合作学习算法能够有效地解决多模态多目标路径规划问题,尤其是在超多目标的多模态路径规划问题中具有很好的应用前景。
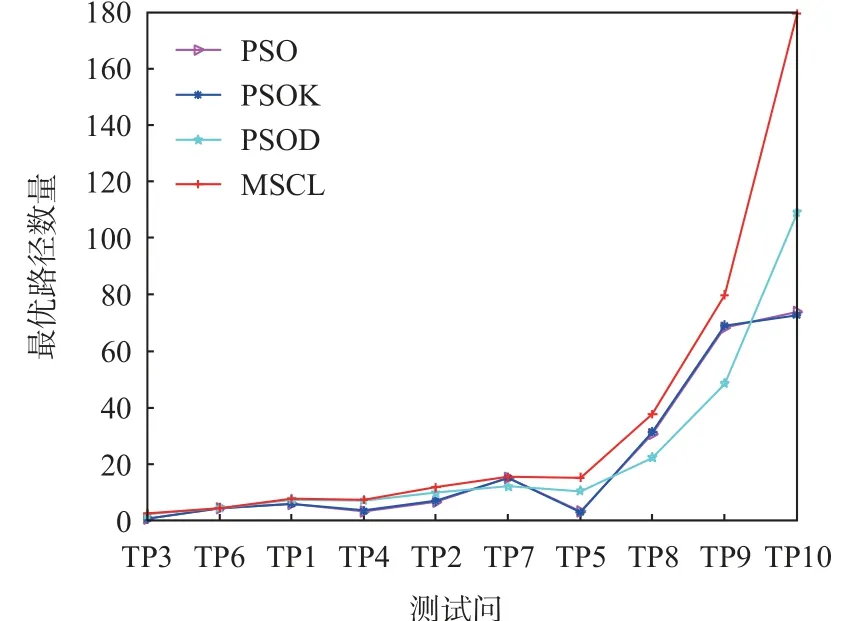
图14 不同算法搜索到的最优路径数量Fig.14 Number of the optimal paths searched by different algorithms
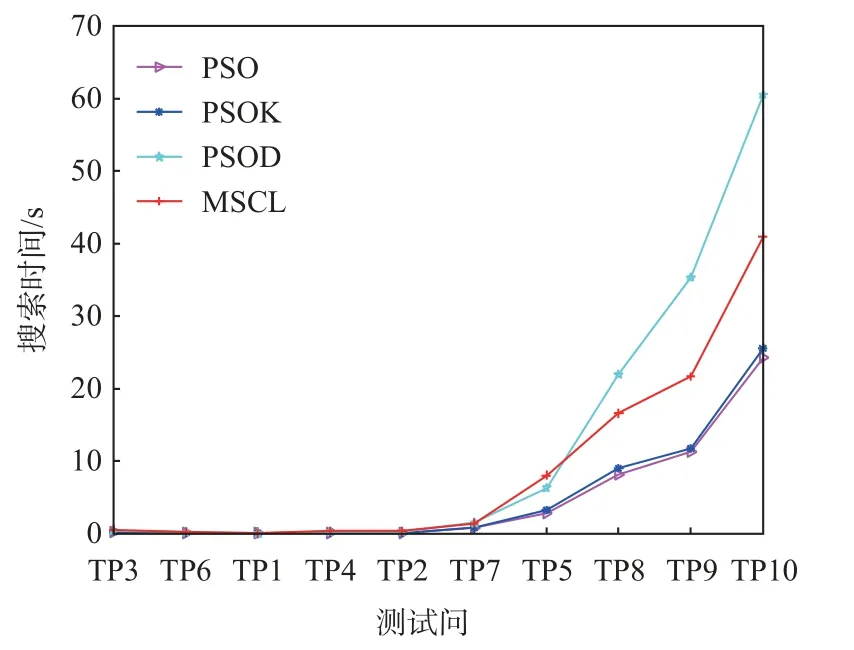
图15 不同算法规划路径所需时间Fig.15 Time used in path planning for different algorithms
4 结 论
1)针对路径规划研究中存在解空间大、编码困难的问题,采用基于关键点的路径编码,该策略可以降低编码维度,提高算法的搜索效率。
2)针对多模态多目标的路径规划需求,考虑在保障算法寻优能力的同时,平衡粒子群在目标空间内不同维度上的搜索能力,提出基于多目标分解的子种群划分。
3)为解决路径规划问题中编解码匹配的不唯一性,提出基于解码经验表的路径解码,通过传递有效的解码经验,降低解码的不确定性,进一步提高算法的寻优能力。
4)基于MMOPP 测试集的实验结果验证了多种群合作学习算法能够有效地解决MMOPP 问题,并且,在复杂的MMOPP 问题中,所提算法的寻优能力更强,最优解的多样性更好,搜索效率受问题规模大小的影响较小。
本文提出的多种群合作学习算法说明了解码经验的有效传递可以提升算法的搜索能力,提高优化问题的求解效率。因此,在后续的研究工作中笔者将继续优化与改进解码经验的传递策略,解决具有多模态多目标优化需求的实际问题。
